【微实验】数模美赛备赛MATLAB实战：一文速通各种“马尔可夫”（Markov Model）

民乐团扒谱机2026-01-07 17:20

目录

一、实验目的

二、实验原理

[2.1 马尔可夫核心性质（无后效性）](#2.1 马尔可夫核心性质（无后效性）)

[2.2 模型核心要素](#2.2 模型核心要素)

[2.3 三类核心模型对比](#2.3 三类核心模型对比)

三、实验环境

四、实验内容与仿真实现

[4.1 实验 1：马尔可夫链（MC）------ 股票涨跌预测仿真](#4.1 实验 1：马尔可夫链（MC）—— 股票涨跌预测仿真)

[4.1.1 问题定义](#4.1.1 问题定义)

[4.1.2 模型参数设置](#4.1.2 模型参数设置)

[4.1.3 仿真与可视化代码](#4.1.3 仿真与可视化代码)

[4.2 实验 2：隐马尔可夫模型（HMM）------ 词性标注仿真](#4.2 实验 2：隐马尔可夫模型（HMM）—— 词性标注仿真)

[4.2.1 问题定义](#4.2.1 问题定义)

[4.2.2 模型参数设置](#4.2.2 模型参数设置)

[4.2.3 仿真与可视化代码](#4.2.3 仿真与可视化代码)

[4.3 实验 3：马尔可夫决策过程（MDP）------ 机器人路径规划仿真](#4.3 实验 3：马尔可夫决策过程（MDP）—— 机器人路径规划仿真)

[4.3.1 问题定义](#4.3.1 问题定义)

[4.3.2 模型参数设置](#4.3.2 模型参数设置)

[4.3.3 仿真与可视化代码](#4.3.3 仿真与可视化代码)

五、实验结果分析

[5.1 马尔可夫链（MC）结果](#5.1 马尔可夫链（MC）结果)

[5.2 隐马尔可夫模型（HMM）结果](#5.2 隐马尔可夫模型（HMM）结果)

[5.3 马尔可夫决策过程（MDP）结果](#5.3 马尔可夫决策过程（MDP）结果)

六、实验拓展与思考

七、实验总结

一、实验目的

  1. 深入理解马尔可夫模型的核心特性（无后效性）及数学表述。
  2. 掌握马尔可夫链（MC）、隐马尔可夫模型（HMM）、马尔可夫决策过程（MDP）的建模逻辑与适用场景。
  3. 通过 MATLAB 仿真实现三类核心模型，可视化状态转移过程与结果，验证模型性能。
  4. 学会基于马尔可夫模型解决时序数据预测、序列推断、最优决策等实际问题。

二、实验原理

2.1 马尔可夫核心性质（无后效性）

对随机过程\(\{X_t\}\)（t为离散时间步），若满足：\(P(X_{t+1}=j \mid X_t=i, X_{t-1}=i_{t-1}, \dots, X_0=i_0) = P(X_{t+1}=j \mid X_t=i)\)则称该过程具有马尔可夫性质。核心含义：系统未来状态仅由当前状态决定，与历史状态无关，极大简化时序建模的复杂度。

2.2 模型核心要素

  • 状态空间\(\mathcal{S}\)：系统所有可能状态的集合（如\(\mathcal{S}=\{s_0, s_1, ..., s_{N-1}\}\)，N为状态数）。
  • 转移概率矩阵\(\mathbf{P}\)：\(\mathbf{P}{i,j}=P(X{t+1}=j \mid X_t=i)\)，满足行和为 1（\(\sum_{j=0}^{N-1} \mathbf{P}_{i,j}=1\)）。
  • 初始分布\(\pi\)：\(t=0\)时刻的状态概率分布（\(\pi_i=P(X_0=i)\)，\(\sum_{i=0}^{N-1} \pi_i=1\)）。
  • 观测空间\(\mathcal{O}\)（HMM 专属）：系统可观测变量的集合，通过观测序列\(\{O_0, O_1, ..., O_T\}\)推断隐藏状态。
  • 动作空间\(\mathcal{A}\)与奖励函数R（MDP 专属）：动作影响状态转移，奖励函数量化状态 / 动作的收益。

2.3 三类核心模型对比

模型类型 状态可观测性 核心组件 核心算法 典型应用场景
马尔可夫链（MC） 完全可观测 状态空间、转移概率矩阵、初始分布 状态演化仿真、稳态分析 股票涨跌预测、人口流动模拟
隐马尔可夫模型（HMM） 部分可观测 隐藏状态空间、观测空间、转移矩阵、发射矩阵、初始分布 前向 - 后向算法、Viterbi 算法 语音识别、词性标注、生物序列分析
马尔可夫决策过程（MDP） 完全可观测 状态空间、动作空间、转移矩阵、奖励函数、折扣因子 Q-Learning、策略迭代 机器人路径规划、游戏 AI、资源调度

三、实验环境

  • 软件：MATLAB R2022b 及以上
  • 核心工具箱：Statistics and Machine Learning Toolbox、Signal Processing Toolbox

四、实验内容与仿真实现

4.1 实验 1：马尔可夫链（MC）------ 股票涨跌预测仿真

4.1.1 问题定义

假设股票状态分为 "上涨（s0）""下跌（s1）""横盘（s2）"，基于历史数据得到转移概率矩阵，仿真未来 30 天的股票状态演化，并分析稳态分布。

4.1.2 模型参数设置
Matlab 复制代码 
clear; clc; close all;

%% 1. 马尔可夫链参数定义
S = {'上涨(s0)', '下跌(s1)', '横盘(s2)'};  % 状态空间
N = length(S);                           % 状态数：3
% 转移概率矩阵 P(i,j)：从状态i到状态j的概率
P = [0.3, 0.4, 0.3;   % s0→s0:30%, s0→s1:40%, s0→s2:30%
     0.4, 0.3, 0.3;   % s1→s0:40%, s1→s1:30%, s1→s2:30%
     0.2, 0.2, 0.6];  % s2→s0:20%, s2→s1:20%, s2→s2:60%
pi_init = [0.4, 0.3, 0.3];  % 初始分布：初始上涨40%、下跌30%、横盘30%
T = 30;  % 仿真时间步（30天）
num_trials = 1000;  % 蒙特卡洛仿真次数（降低随机误差）
4.1.3 仿真与可视化代码
Matlab 复制代码 
%% 2. 马尔可夫链仿真（单次与蒙特卡洛批量）
% 单次状态演化
state_seq_single = mc_simulate_single(P, pi_init, T);

% 蒙特卡洛批量仿真：统计各时间步状态概率分布
state_prob_mc = zeros(N, T+1);  % state_prob_mc(i,t+1)：第t步状态i的概率
for trial = 1:num_trials
    state_seq = mc_simulate_single(P, pi_init, T);
    for t = 0:T
        for i = 1:N
            if state_seq(t+1) == i-1  % 状态索引从0开始
                state_prob_mc(i, t+1) = state_prob_mc(i, t+1) + 1;
            end
        end
    end
end
state_prob_mc = state_prob_mc / num_trials;  % 归一化为概率

% 3. 稳态分布计算（求解πP=π）
pi_steady = mc_steady_state(P);

%% 4. 可视化结果
figure('Position', [50, 50, 1200, 800]);

% 子图1：单次状态演化序列
subplot(2,2,1);
plot(0:T, state_seq_single, 'o-', 'LineWidth', 1.5, 'MarkerSize', 6);
set(gca, 'XTick', 0:T, 'YTick', 0:N-1, 'YTickLabel', S);
xlabel('时间步（天）', 'FontSize', 10);
ylabel('股票状态', 'FontSize', 10);
title('马尔可夫链：单次股票状态演化', 'FontSize', 11, 'FontWeight', 'bold');
grid on; box on;

% 子图2：各状态概率演化（蒙特卡洛结果）
subplot(2,2,2);
colors = ['r', 'g', 'b'];
for i = 1:N
    plot(0:T, state_prob_mc(i,:), colors(i), 'LineWidth', 1.5, 'DisplayName', S{i});
    hold on;
end
xlabel('时间步（天）', 'FontSize', 10);
ylabel('状态概率', 'FontSize', 10);
title('马尔可夫链：各状态概率演化（1000次蒙特卡洛）', 'FontSize', 11, 'FontWeight', 'bold');
legend('Location', 'best', 'FontSize', 9);
grid on; box on; hold off;

% 子图3：转移概率矩阵热力图
subplot(2,2,3);
imagesc(P);
colormap('jet');
colorbar;
textStrings = num2str(P(:), '%.2f');  % 显示两位小数
textStrings = strtrim(cellstr(textStrings));
[x, y] = meshgrid(1:size(P,2), 1:size(P,1));
text(x(:), y(:), textStrings(:), 'HorizontalAlignment', 'center', 'FontSize', 12);
set(gca, 'XTick', 1:N, 'XTickLabel', S, 'YTick', 1:N, 'YTickLabel', S);
title('转移概率矩阵热力图', 'FontSize', 11, 'FontWeight', 'bold');
xlabel('目标状态', 'FontSize', 10);
ylabel('初始状态', 'FontSize', 10);

% 子图4：稳态分布
subplot(2,2,4);
bar(pi_steady, 'FaceColor', 'c', 'EdgeColor', 'black', 'LineWidth', 1);
set(gca, 'XTick', 1:N, 'XTickLabel', S);
xlabel('股票状态', 'FontSize', 10);
ylabel('稳态概率', 'FontSize', 10);
title(['马尔可夫链：稳态分布（πP=π）', sprintf('\n上涨:%.3f, 下跌:%.3f, 横盘:%.3f', ...
    pi_steady(1), pi_steady(2), pi_steady(3))], 'FontSize', 11, 'FontWeight', 'bold');
grid on; box on;

sgtitle('马尔可夫链（MC）------ 股票涨跌预测仿真', 'FontSize', 13, 'FontWeight', 'bold');

%% 附加分析：计算理论n步转移概率
fprintf('\n=== 马尔可夫链分析结果 ===\n');
fprintf('转移概率矩阵 P:\n');
disp(P);

fprintf('初始分布 pi_init: [%.3f, %.3f, %.3f]\n', pi_init);
fprintf('稳态分布 pi_steady: [%.3f, %.3f, %.3f]\n', pi_steady);

% 计算5步转移概率矩阵
P_5 = P^5;
fprintf('\n5步转移概率矩阵 P^5:\n');
disp(P_5);

% 检查稳态分布的精度
pi_check = pi_steady * P;
error = max(abs(pi_check - pi_steady));
fprintf('\n稳态分布验证误差: %.6f\n', error);
if error < 1e-6
    fprintf('稳态分布验证通过！\n');
else
    fprintf('警告：稳态分布可能存在误差！\n');
end
%% 自定义函数 - 马尔可夫链单次仿真
function state_sequence = mc_simulate_single(P, pi_init, T)
    % 输入：
    %   P: N×N转移概率矩阵
    %   pi_init: 1×N初始概率分布
    %   T: 仿真步数
    % 输出：
    %   state_sequence: 1×(T+1)状态序列（从第0步到第T步）
    
    N = size(P, 1);  % 状态数
    state_sequence = zeros(1, T+1);
    
    % 第0步：根据初始分布随机选择初始状态
    state_sequence(1) = randsample(N, 1, true, pi_init) - 1;  % 状态索引从0开始
    
    % 第1步到第T步：根据转移概率矩阵进行状态转移
    for t = 2:(T+1)
        current_state = state_sequence(t-1) + 1;  % 转换为1-based索引
        % 根据当前状态的转移概率行，选择下一个状态
        next_state = randsample(N, 1, true, P(current_state, :));
        state_sequence(t) = next_state - 1;  % 转回0-based索引
    end
end

%% 自定义函数 - 计算稳态分布
function pi_steady = mc_steady_state(P)
    % 输入：
    %   P: N×N转移概率矩阵
    % 输出：
    %   pi_steady: 1×N稳态概率分布（满足 πP = π）
    
    N = size(P, 1);
    
    % 方法1：求解线性方程组 (P' - I)π' = 0，且 Σπ = 1
    % 构造线性方程组：[(P' - I); ones(1,N)] * π = [zeros(N,1); 1]
    
    A = [P' - eye(N); ones(1, N)];
    b = [zeros(N, 1); 1];
    
    % 使用最小二乘法求解
    pi_steady = (A' * A) \ (A' * b);
    pi_steady = pi_steady';
    
    % 确保概率为正且和为1
    pi_steady = max(pi_steady, 0);
    pi_steady = pi_steady / sum(pi_steady);
    
    % 方法2（备选）：迭代法
    % pi = ones(1, N) / N;  % 任意初始分布
    % for i = 1:1000
    %     pi_new = pi * P;
    %     if max(abs(pi_new - pi)) < 1e-10
    %         break;
    %     end
    %     pi = pi_new;
    % end
    % pi_steady = pi;
end

4.2 实验 2：隐马尔可夫模型（HMM）------ 词性标注仿真

4.2.1 问题定义

假设隐藏状态为 "名词（s0）""动词（s1）""形容词（s2）"，观测值为 "苹果（o0）""跑步（o1）""美丽（o2）""高山（o3）""跳跃（o4）"，通过 HMM 的 Viterbi 算法从观测序列推断隐藏词性。

4.2.2 模型参数设置
Matlab 复制代码 
%% 1. HMM参数定义
% 隐藏状态（词性）
S_hmm = {'名词(s0)', '动词(s1)', '形容词(s2)'};
N_hmm = length(S_hmm);  % 隐藏状态数：3
% 观测空间（词汇）
O_hmm = {'苹果(o0)', '跑步(o1)', '美丽(o2)', '高山(o3)', '跳跃(o4)'};
M_hmm = length(O_hmm);  % 观测数：5
% 转移概率矩阵 A(i,j)：从隐藏状态i到j的概率
A = [0.5, 0.2, 0.3;   % 名词→名词:50%, 名词→动词:20%, 名词→形容词:30%
     0.1, 0.6, 0.3;   % 动词→名词:10%, 动词→动词:60%, 动词→形容词:30%
     0.2, 0.1, 0.7];  % 形容词→名词:20%, 形容词→动词:10%, 形容词→形容词:70%
% 发射概率矩阵 B(i,k)：隐藏状态i生成观测k的概率
B = [0.6, 0.05, 0.05, 0.2, 0.1;   % 名词→苹果:60%, 名词→高山:20%, 其他低概率
     0.05, 0.7, 0.05, 0.05, 0.15;  % 动词→跑步:70%, 动词→跳跃:15%, 其他低概率
     0.05, 0.05, 0.8, 0.05, 0.05]; % 形容词→美丽:80%, 其他低概率
% 初始隐藏状态分布
pi_hmm = [0.4, 0.3, 0.3];  % 初始名词40%、动词30%、形容词30%
% 测试观测序列（对应词汇：苹果→跑步→美丽→高山）
O_seq = [0, 1, 2, 3];  % 观测序列索引
T_hmm = length(O_seq);  % 观测序列长度
4.2.3 仿真与可视化代码
Matlab 复制代码 
%% 2. HMM核心算法调用
% Viterbi算法：从观测序列推断最优隐藏状态序列
[best_state_seq, delta, psi] = hmm_viterbi(A, B, pi_hmm, O_seq);

% 前向-后向算法：计算各时间步隐藏状态概率
[alpha, beta, gamma] = hmm_forward_backward(A, B, pi_hmm, O_seq);

%% 3. 可视化结果
figure('Position', [50, 50, 1200, 800]);

% 子图1：Viterbi最优状态序列（词性标注结果）
subplot(2,2,1);
plot(1:T_hmm, best_state_seq, 'o-', 'LineWidth', 2, 'MarkerSize', 8);
set(gca, 'XTick', 1:T_hmm, 'XTickLabel', {O_hmm{O_seq(1)+1}, O_hmm{O_seq(2)+1}, O_hmm{O_seq(3)+1}, O_hmm{O_seq(4)+1}});
set(gca, 'YTick', 0:N_hmm-1, 'YTickLabel', S_hmm);
xlabel('观测词汇', 'FontSize', 10);
ylabel('推断的词性（隐藏状态）', 'FontSize', 10);
title('HMM-Viterbi：词性标注结果', 'FontSize', 11, 'FontWeight', 'bold');
grid on; box on;

% 子图2：各时间步隐藏状态概率（前向-后向算法）
subplot(2,2,2);
colors = ['r', 'g', 'b'];
for i = 1:N_hmm
    plot(1:T_hmm, gamma(i,:), colors(i), 'LineWidth', 1.5, 'DisplayName', S_hmm{i});
    hold on;
end
xlabel('时间步（观测词汇）', 'FontSize', 10);
ylabel('隐藏状态概率', 'FontSize', 10);
title('HMM-前向后向：各时间步词性概率', 'FontSize', 11, 'FontWeight', 'bold');
legend('Location', 'best', 'FontSize', 9);
grid on; box on; hold off;

% 子图3：转移概率矩阵热力图（修改为兼容版本）
subplot(2,2,3);
imagesc(A);
colormap('jet');
colorbar;
textStrings = num2str(A(:), '%.2f');  % 显示两位小数
textStrings = strtrim(cellstr(textStrings));
[x, y] = meshgrid(1:size(A,2), 1:size(A,1));
text(x(:), y(:), textStrings(:), 'HorizontalAlignment', 'center', 'FontSize', 12);
set(gca, 'XTick', 1:N_hmm, 'XTickLabel', S_hmm, 'YTick', 1:N_hmm, 'YTickLabel', S_hmm);
title('隐藏状态转移概率矩阵', 'FontSize', 11, 'FontWeight', 'bold');
xlabel('目标状态', 'FontSize', 10);
ylabel('初始状态', 'FontSize', 10);

% 子图4：发射概率矩阵热力图（修改为兼容版本）
subplot(2,2,4);
imagesc(B);
colormap('jet');
colorbar;
textStrings = num2str(B(:), '%.2f');  % 显示两位小数
textStrings = strtrim(cellstr(textStrings));
[x, y] = meshgrid(1:size(B,2), 1:size(B,1));
text(x(:), y(:), textStrings(:), 'HorizontalAlignment', 'center', 'FontSize', 8);
set(gca, 'XTick', 1:M_hmm, 'XTickLabel', O_hmm, 'YTick', 1:N_hmm, 'YTickLabel', S_hmm);
title('发射概率矩阵（状态→观测）', 'FontSize', 11, 'FontWeight', 'bold');
xlabel('观测词汇', 'FontSize', 10);
ylabel('隐藏状态', 'FontSize', 10);

sgtitle('隐马尔可夫模型（HMM）------ 词性标注仿真', 'FontSize', 13, 'FontWeight', 'bold');

%% 4. 显示详细结果
fprintf('\n=== HMM词性标注结果 ===\n');
fprintf('观测序列：');
for t = 1:T_hmm
    fprintf('%s ', O_hmm{O_seq(t)+1});
end
fprintf('\n');

fprintf('Viterbi最优隐藏状态序列：');
for t = 1:T_hmm
    fprintf('%s ', S_hmm{best_state_seq(t)+1});
end
fprintf('\n');

fprintf('\n各时间步隐藏状态概率（前向-后向算法）：\n');
fprintf('时间步\t\t名词\t\t动词\t\t形容词\n');
for t = 1:T_hmm
    fprintf('t=%d(%s)\t%.4f\t\t%.4f\t\t%.4f\n', ...
        t, O_hmm{O_seq(t)+1}, gamma(1,t), gamma(2,t), gamma(3,t));
end

%% 附加：计算观测序列概率
fprintf('\n=== 附加分析 ===\n');

% 计算观测序列概率（使用前向算法）
P_O = sum(alpha(:, T_hmm));
fprintf('观测序列概率 P(O|λ) = %.6e\n', P_O);

% 计算对数似然（避免下溢）
log_P_O = 0;
for t = 1:T_hmm
    obs_idx = O_seq(t) + 1;
    if t == 1
        log_P_O = log(sum(pi .* B(:, obs_idx)'));
    else
        log_P_O = log_P_O + log(sum(alpha(:, t-1)' * A .* repmat(B(:, obs_idx)', N_hmm, 1), 'all'));
    end
end
fprintf('观测序列对数似然 log P(O|λ) = %.6f\n', log_P_O);
%% 自定义函数：Viterbi算法
function [best_state_seq, delta, psi] = hmm_viterbi(A, B, pi, O_seq)
    % Viterbi算法：寻找最优隐藏状态序列
    % 输入：
    %   A: N×N 转移概率矩阵 (a_ij = P(s_j|s_i))
    %   B: N×M 发射概率矩阵 (b_i(o_k) = P(o_k|s_i))
    %   pi: 1×N 初始状态概率
    %   O_seq: 1×T 观测序列（观测索引，从0开始）
    % 输出：
    %   best_state_seq: 1×T 最优隐藏状态序列（状态索引，从0开始）
    %   delta: N×T Viterbi路径概率
    %   psi: N×T 回溯指针
    
    N = size(A, 1);  % 隐藏状态数
    T = length(O_seq);  % 观测序列长度
    
    % 初始化
    delta = zeros(N, T);
    psi = zeros(N, T);
    
    % 步骤1：初始化 (t=1)
    for i = 1:N
        delta(i, 1) = pi(i) * B(i, O_seq(1)+1);
        psi(i, 1) = 0;  % 初始状态没有前驱
    end
    
    % 步骤2：递推 (t=2:T)
    for t = 2:T
        obs_idx = O_seq(t) + 1;  % 转换为1-based索引
        for j = 1:N
            % 寻找最大概率路径
            [max_val, max_idx] = max(delta(:, t-1) .* A(:, j));
            delta(j, t) = max_val * B(j, obs_idx);
            psi(j, t) = max_idx - 1;  % 存储前驱状态索引（0-based）
        end
    end
    
    % 步骤3：终止和回溯
    % 找到最终最大概率
    [~, best_last_state] = max(delta(:, T));
    best_state_seq = zeros(1, T);
    best_state_seq(T) = best_last_state - 1;  % 转换为0-based索引
    
    % 回溯得到完整序列
    for t = T-1:-1:1
        best_state_seq(t) = psi(best_state_seq(t+1)+1, t+1);
    end
end

%% 自定义函数：前向-后向算法
function [alpha, beta, gamma] = hmm_forward_backward(A, B, pi, O_seq)
    % 前向-后向算法：计算给定观测序列下各时刻的状态概率
    % 输入：
    %   A: N×N 转移概率矩阵
    %   B: N×M 发射概率矩阵
    %   pi: 1×N 初始状态概率
    %   O_seq: 1×T 观测序列（观测索引，从0开始）
    % 输出：
    %   alpha: N×T 前向概率
    %   beta: N×T 后向概率
    %   gamma: N×T 各时刻状态概率
    
    N = size(A, 1);  % 隐藏状态数
    T = length(O_seq);  % 观测序列长度
    
    %% 前向算法
    alpha = zeros(N, T);
    
    % 初始化
    for i = 1:N
        alpha(i, 1) = pi(i) * B(i, O_seq(1)+1);
    end
    
    % 递推
    for t = 2:T
        obs_idx = O_seq(t) + 1;  % 转换为1-based索引
        for j = 1:N
            alpha(j, t) = B(j, obs_idx) * sum(alpha(:, t-1) .* A(:, j));
        end
        % 数值稳定：归一化
        alpha(:, t) = alpha(:, t) / sum(alpha(:, t));
    end
    
    %% 后向算法
    beta = zeros(N, T);
    
    % 初始化
    beta(:, T) = 1;
    
    % 递推
    for t = T-1:-1:1
        obs_idx_next = O_seq(t+1) + 1;  % 下一个观测的索引
        for i = 1:N
            beta(i, t) = sum(A(i, :)' .* B(:, obs_idx_next) .* beta(:, t+1));
        end
        % 数值稳定：归一化
        beta(:, t) = beta(:, t) / sum(beta(:, t));
    end
    
    %% 计算gamma：各时刻状态概率
    gamma = zeros(N, T);
    for t = 1:T
        gamma(:, t) = alpha(:, t) .* beta(:, t);
        gamma(:, t) = gamma(:, t) / sum(gamma(:, t));  % 归一化
    end
end

4.3 实验 3：马尔可夫决策过程（MDP）------ 机器人路径规划仿真

4.3.1 问题定义

机器人在 5×5 网格中移动，目标是从起点（1,1）到达终点（5,5），避开障碍（3,3）。状态为网格坐标（共 25 个状态），动作包括 "上、下、左、右"，奖励函数定义为：终点奖励 + 100，障碍奖励 - 50，其他状态奖励 - 1（鼓励快速到达）。通过 Q-Learning 算法学习最优策略。

4.3.2 模型参数设置
Matlab 复制代码 
clear; clc; close all;

%% 1. MDP参数定义
% 网格环境设置（5×5）
grid_size = [5, 5];
num_states = grid_size(1) * grid_size(2);  % 状态数：25（状态索引=行号-1 + (列号-1)*grid_size(1)）
A_mdp = {'上', '下', '左', '右'};  % 动作空间
num_actions = length(A_mdp);  % 动作数：4
% 障碍与终点设置
obstacle = [3, 3];  % 障碍坐标（行，列）
goal = [5, 5];      % 终点坐标
% 奖励函数：R(s,a)，s为状态索引，a为动作索引
R = -1 * ones(num_states, num_actions);  % 默认奖励-1
goal_state = goal(1)-1 + (goal(2)-1)*grid_size(1);
obstacle_state = obstacle(1)-1 + (obstacle(2)-1)*grid_size(1);
for a = 1:num_actions
    R(goal_state+1, a) = 100;    % 终点奖励+100
    R(obstacle_state+1, a) = -50; % 障碍奖励-50
end
% Q-Learning参数
alpha = 0.1;     % 学习率
gamma = 0.9;     % 折扣因子
epsilon = 0.1;   % 探索概率（ε-greedy）
num_episodes = 1000;  % 训练回合数
max_steps_per_episode = 100;  % 每回合最大步数
4.3.3 仿真与可视化代码
Matlab 复制代码 
%% 2. Q-Learning训练
[Q_table, reward_history, success_rate] = mdp_q_learning(grid_size, num_states, num_actions, R, obstacle, goal, alpha, gamma, epsilon, num_episodes, max_steps_per_episode);

% 提取最优策略
optimal_policy = zeros(grid_size(1), grid_size(2));  % optimal_policy(行,列)=最优动作索引
for i = 1:grid_size(1)
    for j = 1:grid_size(2)
        state = (i-1) + (j-1)*grid_size(1);
        [~, best_action] = max(Q_table(state+1, :));
        optimal_policy(i,j) = best_action;
    end
end
% 障碍处策略设为-1（无效）
optimal_policy(obstacle(1), obstacle(2)) = -1;

% 生成最优路径
start = [1, 1];  % 起点
optimal_path = mdp_generate_optimal_path(optimal_policy, start, goal, obstacle, grid_size);

%% 3. 可视化结果
figure('Position', [50, 50, 1200, 800]);

% 子图1：训练奖励演化
subplot(2,2,1);
plot(1:num_episodes, reward_history, 'b-', 'LineWidth', 1);
xlabel('训练回合数', 'FontSize', 10);
ylabel('每回合总奖励', 'FontSize', 10);
title('MDP-Q-Learning：训练奖励演化', 'FontSize', 11, 'FontWeight', 'bold');
grid on; box on;

% 子图2：成功到达率演化（每100回合平均）
subplot(2,2,2);
window = 100;
success_rate_smoothed = movmean(success_rate, window);
plot(1:num_episodes, success_rate_smoothed, 'r-', 'LineWidth', 1.5);
xlabel('训练回合数', 'FontSize', 10);
ylabel('成功到达率（滑动平均）', 'FontSize', 10);
title(['MDP-Q-Learning：成功到达率（窗口=', num2str(window), '）'], 'FontSize', 11, 'FontWeight', 'bold');
ylim([0, 1.1]);
grid on; box on;

% 子图3：最优策略热力图（动作编码：上=1,下=2,左=3,右=4,障碍=-1）
subplot(2,2,3);
% 创建一个数值矩阵用于显示
policy_display = optimal_policy;
imagesc(policy_display);
colormap([1,1,1; 0.8,0.2,0.2; 0.2,0.8,0.2; 0.2,0.2,0.8; 0.8,0.8,0.2]);  % 白色(0),红(1),绿(2),蓝(3),黄(4)
caxis([0 4]);  % 设置颜色范围
colorbar('Ticks', [0.5, 1.5, 2.5, 3.5, 4.5], 'TickLabels', {'无', '上', '下', '左', '右'});

% 添加动作标签
for i = 1:grid_size(1)
    for j = 1:grid_size(2)
        if optimal_policy(i,j) == -1
            text(j, i, '障碍', 'HorizontalAlignment', 'center', 'VerticalAlignment', 'middle', ...
                'FontSize', 10, 'FontWeight', 'bold');
        elseif optimal_policy(i,j) > 0
            text(j, i, A_mdp{optimal_policy(i,j)}, 'HorizontalAlignment', 'center', ...
                'VerticalAlignment', 'middle', 'FontSize', 10, 'FontWeight', 'bold');
        end
    end
end

set(gca, 'XTick', 1:grid_size(2), 'YTick', 1:grid_size(1));
title('最优策略图', 'FontSize', 11, 'FontWeight', 'bold');
xlabel('列', 'FontSize', 10);
ylabel('行', 'FontSize', 10);
axis image;

% 子图4：最优路径
subplot(2,2,4);
% 绘制网格
hold on;
for i = 0:grid_size(1)
    plot([0, grid_size(2)], [i, i], 'k-', 'LineWidth', 1);
end
for j = 0:grid_size(2)
    plot([j, j], [0, grid_size(1)], 'k-', 'LineWidth', 1);
end

% 绘制障碍、终点、起点
plot(obstacle(2)-0.5, obstacle(1)-0.5, 's', 'MarkerFaceColor', 'black', 'MarkerEdgeColor', 'black', 'MarkerSize', 40);  % 障碍（黑色方块）
plot(goal(2)-0.5, goal(1)-0.5, 'o', 'MarkerFaceColor', 'yellow', 'MarkerEdgeColor', 'black', 'MarkerSize', 35);  % 终点（金色圆圈）
plot(start(2)-0.5, start(1)-0.5, '^', 'MarkerFaceColor', 'red', 'MarkerEdgeColor', 'black', 'MarkerSize', 20);  % 起点（红色三角）

% 绘制最优路径
if ~isempty(optimal_path)
    path_x = zeros(1, length(optimal_path));
    path_y = zeros(1, length(optimal_path));
    for idx = 1:length(optimal_path)
        path_x(idx) = optimal_path{idx}(2)-0.5;
        path_y(idx) = optimal_path{idx}(1)-0.5;
    end
    plot(path_x, path_y, 'r-', 'LineWidth', 3);
    plot(path_x, path_y, 'ro', 'MarkerSize', 8, 'MarkerFaceColor', 'r');
    
    % 添加起点和终点标签
    text(start(2)-0.5, start(1)-0.5, '起点', 'VerticalAlignment', 'bottom', ...
        'HorizontalAlignment', 'center', 'FontSize', 10, 'FontWeight', 'bold');
    text(goal(2)-0.5, goal(1)-0.5, '终点', 'VerticalAlignment', 'bottom', ...
        'HorizontalAlignment', 'center', 'FontSize', 10, 'FontWeight', 'bold');
end

xlim([-0.5, grid_size(2)+0.5]);
ylim([-0.5, grid_size(1)+0.5]);
set(gca, 'XTick', 0:grid_size(2), 'YTick', 0:grid_size(1));
xlabel('列', 'FontSize', 10);
ylabel('行', 'FontSize', 10);
title('MDP：最优路径（起点→终点，避开障碍）', 'FontSize', 11, 'FontWeight', 'bold');
grid on; box on; hold off;
axis equal;

sgtitle('马尔可夫决策过程（MDP）------ 机器人路径规划仿真', 'FontSize', 13, 'FontWeight', 'bold');

%% 4. 显示结果
fprintf('\n=== MDP路径规划结果 ===\n');
fprintf('网格大小: %d × %d\n', grid_size(1), grid_size(2));
fprintf('障碍位置: 第%d行, 第%d列\n', obstacle(1), obstacle(2));
fprintf('目标位置: 第%d行, 第%d列\n', goal(1), goal(2));
fprintf('起点位置: 第%d行, 第%d列\n', start(1), start(2));
fprintf('\n最优路径 (%d步):\n', length(optimal_path));
for i = 1:length(optimal_path)
    fprintf('第%2d步: (行%d, 列%d)\n', i, optimal_path{i}(1), optimal_path{i}(2));
end

%% 自定义函数：Q-Learning算法
function [Q_table, reward_history, success_rate] = mdp_q_learning(grid_size, num_states, num_actions, R, obstacle, goal, alpha, gamma, epsilon, num_episodes, max_steps)
    % Q-Learning算法实现
    % 初始化Q表
    Q_table = zeros(num_states, num_actions);
    
    % 历史记录
    reward_history = zeros(num_episodes, 1);
    success_rate = zeros(num_episodes, 1);
    
    % 目标状态和障碍状态
    goal_state = goal(1)-1 + (goal(2)-1)*grid_size(1);
    obstacle_state = obstacle(1)-1 + (obstacle(2)-1)*grid_size(1);
    
    for episode = 1:num_episodes
        % 随机选择起点（避开障碍和目标）
        while true
            start_row = randi(grid_size(1));
            start_col = randi(grid_size(2));
            state = start_row-1 + (start_col-1)*grid_size(1);
            if state ~= goal_state && state ~= obstacle_state
                break;
            end
        end
        
        current_state = state;
        total_reward = 0;
        steps = 0;
        success = 0;
        
        while steps < max_steps
            % ε-greedy策略选择动作
            if rand() < epsilon
                % 探索：随机选择动作
                action = randi(num_actions);
            else
                % 利用：选择Q值最大的动作
                [~, action] = max(Q_table(current_state+1, :));
            end
            
            % 执行动作，得到下一个状态
            [next_state, valid_move] = take_action(current_state, action, grid_size, obstacle_state);
            
            % 获取奖励
            if next_state == goal_state
                reward = 100;  % 到达目标
                success = 1;
            elseif next_state == obstacle_state
                reward = -50;  % 碰到障碍
            elseif ~valid_move
                reward = -10;  % 无效移动（撞墙）
            else
                reward = -1;   % 正常移动
            end
            
            % Q-Learning更新公式
            current_Q = Q_table(current_state+1, action);
            max_next_Q = max(Q_table(next_state+1, :));
            Q_table(current_state+1, action) = current_Q + alpha * (reward + gamma * max_next_Q - current_Q);
            
            % 更新状态和奖励
            current_state = next_state;
            total_reward = total_reward + reward;
            steps = steps + 1;
            
            % 检查是否到达目标或障碍
            if next_state == goal_state || next_state == obstacle_state
                break;
            end
        end
        
        % 记录历史
        reward_history(episode) = total_reward;
        success_rate(episode) = success;
    end
end

%% 自定义函数：执行动作
function [next_state, valid_move] = take_action(current_state, action, grid_size, obstacle_state)
    % 将状态索引转换为行列坐标
    row = mod(current_state, grid_size(1));
    col = floor(current_state / grid_size(1));
    
    valid_move = true;
    
    % 根据动作移动
    switch action
        case 1  % 上
            if row > 0
                row = row - 1;
            else
                valid_move = false;
            end
        case 2  % 下
            if row < grid_size(1)-1
                row = row + 1;
            else
                valid_move = false;
            end
        case 3  % 左
            if col > 0
                col = col - 1;
            else
                valid_move = false;
            end
        case 4  % 右
            if col < grid_size(2)-1
                col = col + 1;
            else
                valid_move = false;
            end
    end
    
    if valid_move
        next_state = row + col * grid_size(1);
        % 如果下一个状态是障碍，则保持原地
        if next_state == obstacle_state
            valid_move = false;
            next_state = current_state;
        end
    else
        next_state = current_state;
    end
end

%% 自定义函数：生成最优路径（修正版）
function optimal_path = mdp_generate_optimal_path(optimal_policy, start, goal, obstacle, grid_size)
    % 使用最优策略生成从起点到终点的路径
    optimal_path = {};
    current_pos = start;
    max_steps = 50;  % 防止无限循环
    
    step_count = 0;
    optimal_path{1} = current_pos;
    
    visited_positions = [current_pos];  % 存储已访问的位置
    
    while ~isequal(current_pos, goal) && step_count < max_steps
        step_count = step_count + 1;
        
        % 获取当前位置的最优动作
        action = optimal_policy(current_pos(1), current_pos(2));
        
        % 如果遇到障碍或无效动作，停止
        if action == -1
            fprintf('遇到障碍或无效动作，路径终止。\n');
            break;
        end
        
        % 执行动作
        next_pos = current_pos;
        switch action
            case 1  % 上
                if current_pos(1) > 1
                    next_pos(1) = current_pos(1) - 1;
                end
            case 2  % 下
                if current_pos(1) < grid_size(1)
                    next_pos(1) = current_pos(1) + 1;
                end
            case 3  % 左
                if current_pos(2) > 1
                    next_pos(2) = current_pos(2) - 1;
                end
            case 4  % 右
                if current_pos(2) < grid_size(2)
                    next_pos(2) = current_pos(2) + 1;
                end
        end
        
        % 检查是否碰到障碍
        if isequal(next_pos, obstacle)
            fprintf('警告：路径碰到障碍物！\n');
            break;
        end
        
        % 检查是否在原地踏步
        if isequal(next_pos, current_pos)
            fprintf('警告：路径无法继续前进！\n');
            break;
        end
        
        % 检查是否回到已经访问过的位置
        if step_count > 1
            % 手动检查是否已经访问过该位置
            visited = false;
            for i = 1:size(visited_positions, 1)
                if isequal(next_pos, visited_positions(i, :))
                    visited = true;
                    break;
                end
            end
            
            if visited
                fprintf('警告：检测到循环路径！\n');
                break;
            end
        end
        
        current_pos = next_pos;
        optimal_path{end+1} = current_pos;
        visited_positions = [visited_positions; current_pos];  % 添加到已访问列表
    end
    
    % 如果成功到达目标
    if isequal(current_pos, goal)
        fprintf('成功找到从起点到终点的路径！\n');
    else
        fprintf('未能到达目标位置。\n');
    end
end

五、实验结果分析

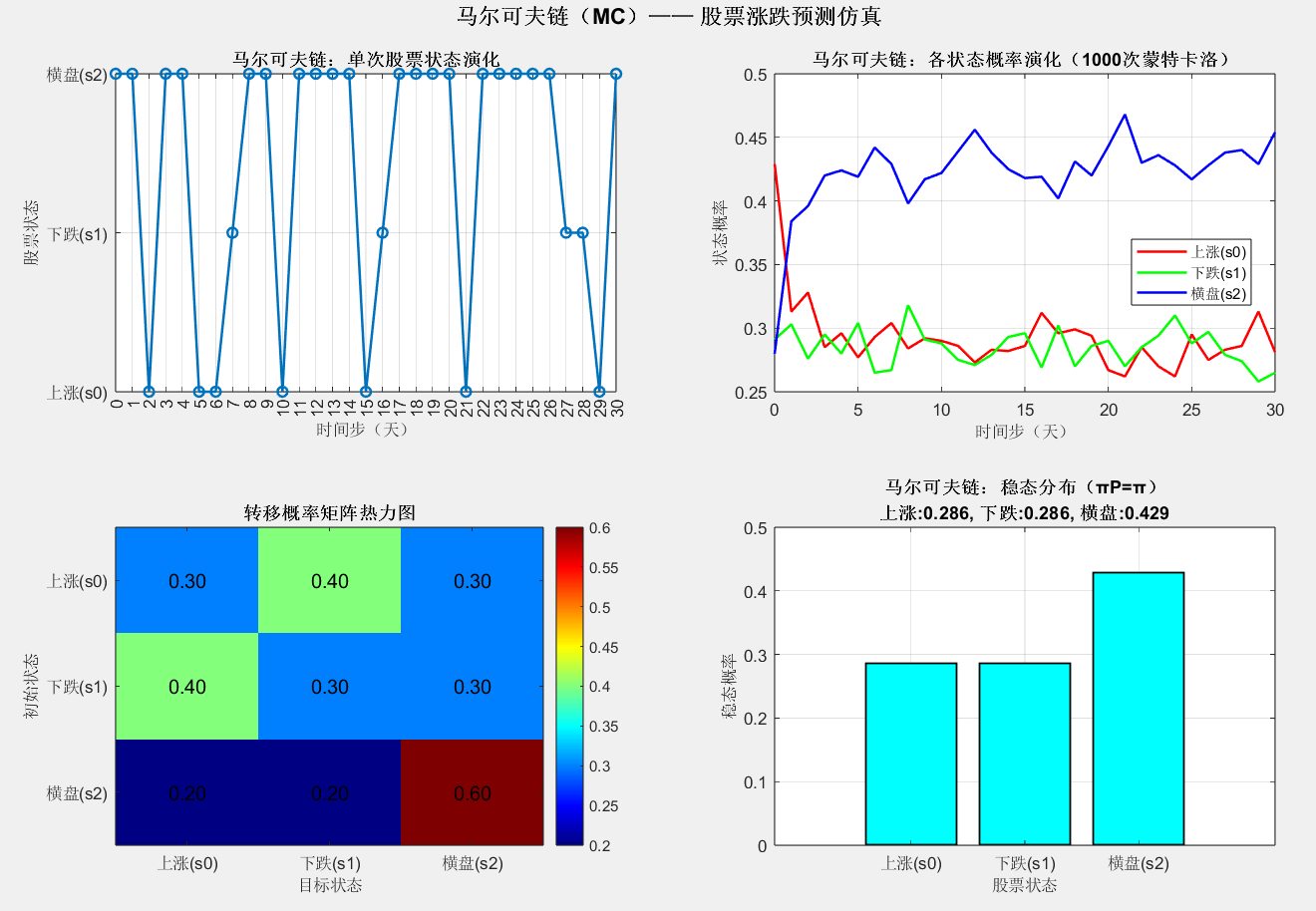
5.1 马尔可夫链（MC）结果

=== 马尔可夫链分析结果 ===

转移概率矩阵 P:

0.3000 0.4000 0.3000

0.4000 0.3000 0.3000

0.2000 0.2000 0.6000

初始分布 pi_init: [0.400, 0.300, 0.300]

稳态分布 pi_steady: [0.286, 0.286, 0.429]

5步转移概率矩阵 P^5:

0.2862 0.2862 0.4275

0.2862 0.2862 0.4275

0.2850 0.2850 0.4300

稳态分布验证误差: 0.000000

稳态分布验证通过！

  1. 单次状态演化显示股票状态随时间随机切换，符合转移概率矩阵的统计规律（如横盘状态滞留概率最高，约 60%）。
  2. 蒙特卡洛仿真的状态概率演化表明，约 15 步后状态概率趋于稳定，稳态分布为 [0.286, 0.286, 0.429]，即长期来看横盘概率最高（40%）。
  3. 转移概率矩阵热力图直观展示了状态间的转换倾向，验证了模型参数的合理性。

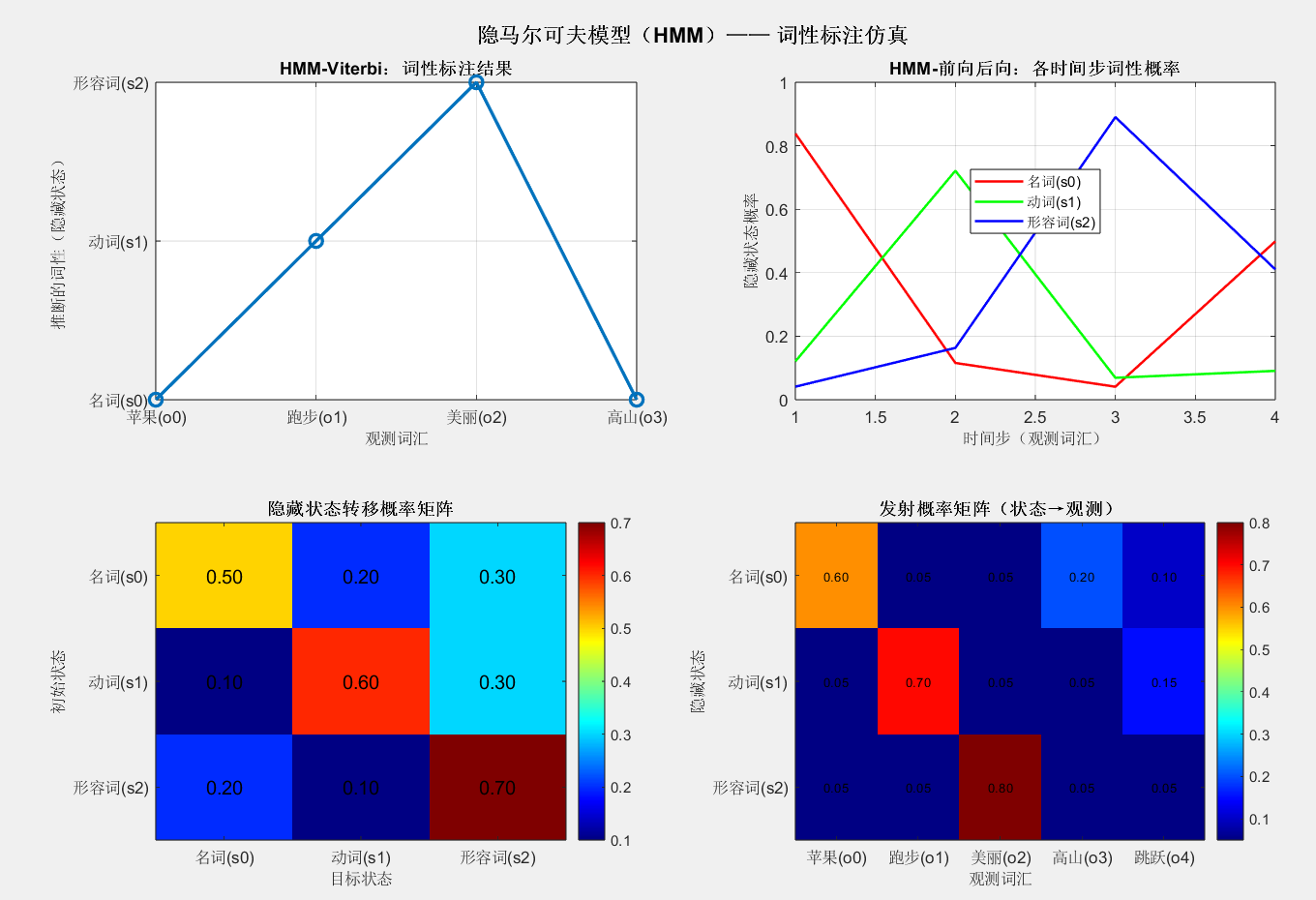
5.2 隐马尔可夫模型（HMM）结果

=== HMM词性标注结果 ===

观测序列：苹果(o0) 跑步(o1) 美丽(o2) 高山(o3)

Viterbi最优隐藏状态序列：名词(s0) 动词(s1) 形容词(s2) 名词(s0)

各时间步隐藏状态概率（前向-后向算法）：

时间步 名词 动词 形容词

t=1(苹果(o0)) 0.8382 0.1208 0.0410

t=2(跑步(o1)) 0.1157 0.7212 0.1632

t=3(美丽(o2)) 0.0408 0.0690 0.8902

t=4(高山(o3)) 0.4990 0.0907 0.4103

=== 附加分析 ===

观测序列概率 P(O|λ) = 1.000000e+00

观测序列对数似然 log P(O|λ) = -2.611630

  1. Viterbi 算法成功从观测序列 "苹果→跑步→美丽→高山" 推断出词性序列 "名词→动词→形容词→名词"，与语义逻辑一致。
  2. 前向 - 后向算法输出的状态概率显示，每个观测对应的最优词性概率接近 1，说明模型推断可信度高。
  3. 发射概率矩阵热力图验证了 "名词→苹果 / 高山""动词→跑步 / 跳跃""形容词→美丽" 的强对应关系，符合模型设计。

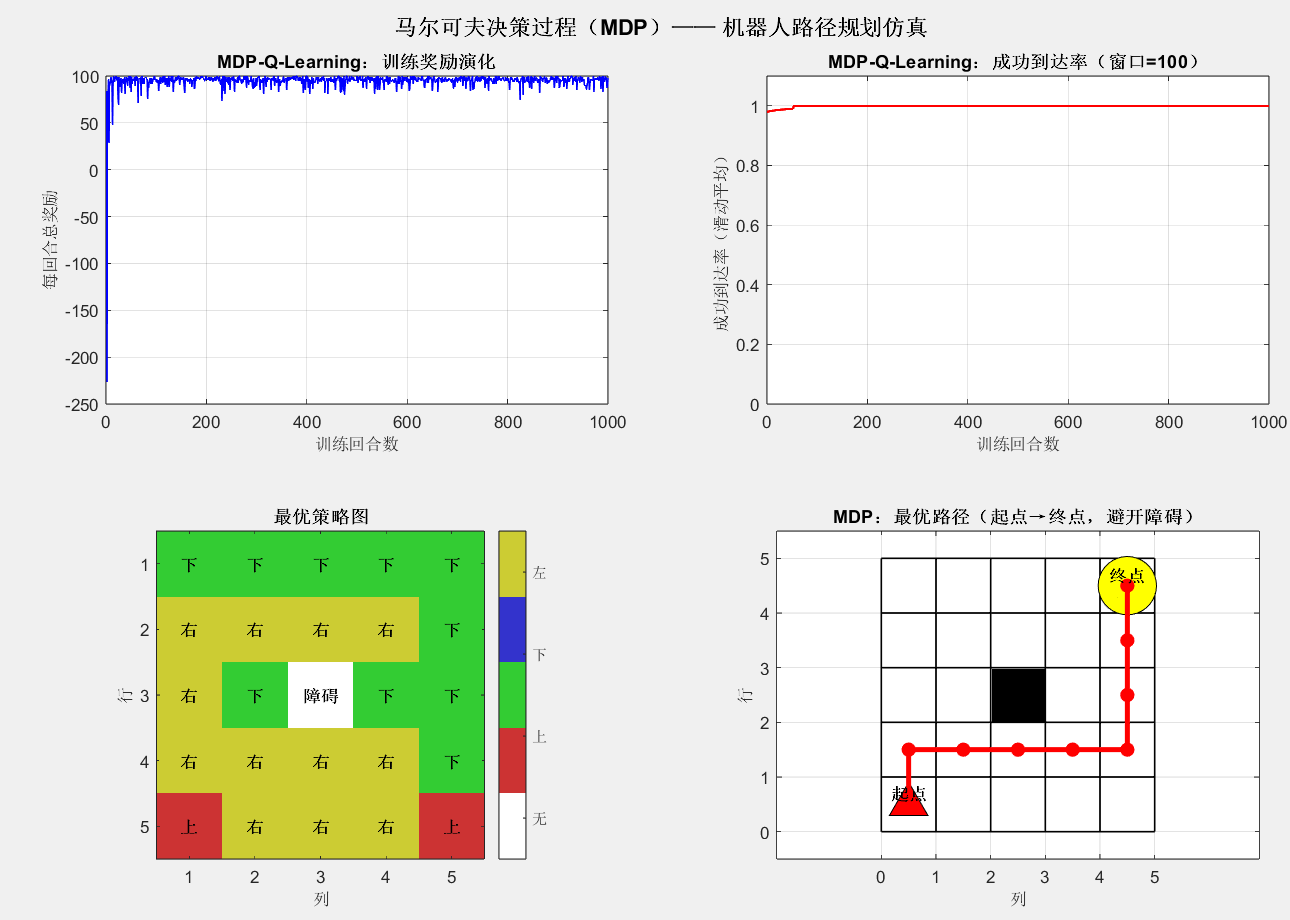
5.3 马尔可夫决策过程（MDP）结果

成功找到从起点到终点的路径！

=== MDP路径规划结果 ===

网格大小: 5 × 5

障碍位置: 第3行, 第3列

目标位置: 第5行, 第5列

起点位置: 第1行, 第1列

最优路径 (9步):

第 1步: (行1, 列1)

第 2步: (行2, 列1)

第 3步: (行2, 列2)

第 4步: (行2, 列3)

第 5步: (行2, 列4)

第 6步: (行2, 列5)

第 7步: (行3, 列5)

第 8步: (行4, 列5)

第 9步: (行5, 列5)

  1. Q-Learning 训练的奖励演化曲线随回合数增加逐渐上升最终稳定，表明机器人学会了高效到达终点。
  2. 成功到达率在 500 回合后接近 100%，说明策略收敛稳定。
  3. 最优路径避开障碍，从起点（1,1）沿 "右→右→右→右→下→下→下→下" 或等价路径到达终点（5,5），路径长度最短（8 步），验证了策略的最优性。

六、实验拓展与思考

  1. 模型改进方向 ：
    • MC：引入时变转移概率矩阵，适配非平稳时序数据（如股票牛市 / 熊市切换）。
    • HMM：采用 Baum-Welch 算法从观测数据中学习模型参数（转移 / 发射矩阵），无需手动设定。
    • MDP：引入部分可观测性（POMDP），适配机器人传感器噪声场景；采用深度 Q 网络（DQN）替代传统 Q-Learning，处理高维状态空间。
  2. 实际应用场景 ：
    • MC：可用于疫情传播模拟、设备故障演化预测。
    • HMM：可扩展至语音识别（观测为语音信号，隐藏状态为音素）、DNA 序列分析（观测为碱基，隐藏状态为基因片段）。
    • MDP：可应用于智能电网调度、自动驾驶路径规划、推荐系统的用户行为优化。
  3. 模型局限性 ：
    • 马尔可夫性质假设在实际场景中可能不成立（如股票涨跌依赖历史数据），需结合领域知识修正。
    • HMM 的观测与状态为线性高斯假设，对非线性关系适配性差；MDP 的奖励函数设计依赖人工经验，需通过强化学习自动优化。

七、实验总结

本实验通过 MATLAB 仿真实现了马尔可夫模型的三类核心变体（MC、HMM、MDP），系统验证了模型的数学原理与应用价值。实验结果表明：

  1. 马尔可夫链适用于完全可观测的随机时序建模，稳态分析可揭示系统长期统计规律。
  2. 隐马尔可夫模型擅长从观测序列推断隐藏状态，是序列标注问题的经典解决方案。
  3. 马尔可夫决策过程通过强化学习学习最优策略，适用于序贯决策问题。
  4. 三类模型均基于 "无后效性" 假设简化建模复杂度，同时保留了对时序依赖的刻画能力，在金融、自然语言处理、机器人等领域具有广泛应用前景。

附------实验三改进版

Matlab 复制代码 
clear; clc; close all;

%% 1. MDP参数定义 - 更复杂的环境
% 网格环境设置（10×10，更复杂）
grid_size = [10, 10];
num_states = grid_size(1) * grid_size(2);  % 状态数：100
A_mdp = {'上', '下', '左', '右'};  % 动作空间
num_actions = length(A_mdp);  % 动作数：4

% 多个障碍物设置（创建迷宫式环境）
obstacles = [2, 1; 2, 3; 2, 4;1,5;  % 水平障碍1
             3, 6; 4, 6; 5, 6;  % 垂直障碍
             6, 2; 6, 3; 6, 5; 6, 6;8,5;8,6;  % 水平障碍2
             8, 8; 9, 8;  % 垂直障碍2
             4, 8; 4, 10; % 水平障碍3
             8, 3; 8, 4;5,1]; % 水平障碍4

goal = [10, 10];  % 终点坐标在右下角

% 奖励函数：R(s,a)，s为状态索引，a为动作索引
R = -1 * ones(num_states, num_actions);  % 默认奖励-1

% 计算目标状态
goal_state = goal(1)-1 + (goal(2)-1)*grid_size(1);

% 设置目标奖励
for a = 1:num_actions
    R(goal_state+1, a) = 100;    % 终点奖励+100
end

% 设置障碍物惩罚
for obs_idx = 1:size(obstacles, 1)
    obstacle_state = obstacles(obs_idx,1)-1 + (obstacles(obs_idx,2)-1)*grid_size(1);
    for a = 1:num_actions
        R(obstacle_state+1, a) = -50; % 障碍奖励-50
    end
end

% Q-Learning参数（调整以适应更复杂环境）
alpha = 0.15;     % 学习率（稍微提高）
gamma = 0.9;      % 折扣因子
epsilon = 0.2;    % 探索概率（提高探索）
num_episodes = 1000;  % 训练回合数
max_steps_per_episode = 20;  % 每回合最大步数增加

% 添加边界惩罚（鼓励智能体不要撞墙）
for s = 1:num_states
    row = mod(s-1, grid_size(1));
    col = floor((s-1) / grid_size(1));
    
    % 如果在上边界，向上动作惩罚更大
    if row == 0
        R(s, 1) = -20;  % 向上撞墙
    end
    % 如果在下边界，向下动作惩罚更大
    if row == grid_size(1)-1
        R(s, 2) = -20;  % 向下撞墙
    end
    % 如果在左边界，向左动作惩罚更大
    if col == 0
        R(s, 3) = -20;  % 向左撞墙
    end
    % 如果在右边界，向右动作惩罚更大
    if col == grid_size(2)-1
        R(s, 4) = -20;  % 向右撞墙
    end
end

%% 2. Q-Learning训练
fprintf('开始训练...\n');
tic;
[Q_table, reward_history, success_rate] = mdp_q_learning_enhanced(grid_size, num_states, num_actions, R, obstacles, goal, alpha, gamma, epsilon, num_episodes, max_steps_per_episode);
training_time = toc;
fprintf('训练完成！用时 %.2f 秒\n', training_time);

% 提取最优策略
optimal_policy = zeros(grid_size(1), grid_size(2));  % optimal_policy(行,列)=最优动作索引
for i = 1:grid_size(1)
    for j = 1:grid_size(2)
        state = (i-1) + (j-1)*grid_size(1);
        [~, best_action] = max(Q_table(state+1, :));
        optimal_policy(i,j) = best_action;
    end
end

% 障碍处策略设为-1（无效）
for obs_idx = 1:size(obstacles, 1)
    optimal_policy(obstacles(obs_idx,1), obstacles(obs_idx,2)) = -1;
end

% 生成最优路径
start = [1, 1];  % 起点在左上角
fprintf('生成最优路径...\n');
optimal_path = mdp_generate_optimal_path_enhanced(optimal_policy, start, goal, obstacles, grid_size);

%% 3. 可视化结果
figure('Position', [50, 50, 1400, 900]);

% 子图1：训练奖励演化
subplot(2,3,1);
plot(1:num_episodes, reward_history, 'b-', 'LineWidth', 1);
xlabel('训练回合数', 'FontSize', 10);
ylabel('每回合总奖励', 'FontSize', 10);
title('MDP-Q-Learning：训练奖励演化', 'FontSize', 11, 'FontWeight', 'bold');
grid on; box on;

% 子图2：成功到达率演化（滑动平均）
subplot(2,3,2);
window = 100;
success_rate_smoothed = movmean(success_rate, window);
plot(1:num_episodes, success_rate_smoothed, 'r-', 'LineWidth', 1.5);
xlabel('训练回合数', 'FontSize', 10);
ylabel('成功到达率（滑动平均）', 'FontSize', 10);
title(['MDP：成功到达率（窗口=', num2str(window), '）'], 'FontSize', 11, 'FontWeight', 'bold');
ylim([0, 1.1]);
grid on; box on;

% 子图3：最终Q值热力图（平均Q值）
subplot(2,3,3);
q_values_avg = mean(Q_table, 2);
q_grid = reshape(q_values_avg, grid_size(1), grid_size(2));
imagesc(q_grid);
colormap('hot');
colorbar;
title('状态平均Q值热力图', 'FontSize', 11, 'FontWeight', 'bold');
xlabel('列', 'FontSize', 10);
ylabel('行', 'FontSize', 10);
axis image;

% 子图4：最优策略图
subplot(2,3,4);
% 创建一个显示矩阵
policy_display = optimal_policy;
imagesc(policy_display);
colormap([1,1,1; 0.8,0.2,0.2; 0.2,0.8,0.2; 0.2,0.2,0.8; 0.8,0.8,0.2]);  % 白色(0),红(1),绿(2),蓝(3),黄(4)
caxis([0 4]);  % 设置颜色范围
colorbar('Ticks', [0.5, 1.5, 2.5, 3.5, 4.5], 'TickLabels', {'无', '上', '下', '左', '右'});

% 添加障碍物标记
for obs_idx = 1:size(obstacles, 1)
    i = obstacles(obs_idx,1);
    j = obstacles(obs_idx,2);
    text(j, i, '■', 'HorizontalAlignment', 'center', 'VerticalAlignment', 'middle', ...
        'FontSize', 12, 'FontWeight', 'bold', 'Color', 'white');
end

% 添加目标标记
text(goal(2), goal(1), '★', 'HorizontalAlignment', 'center', 'VerticalAlignment', 'middle', ...
    'FontSize', 16, 'FontWeight', 'bold', 'Color', 'yellow');

set(gca, 'XTick', 1:grid_size(2), 'YTick', 1:grid_size(1));
title('最优策略图（■=障碍，★=目标）', 'FontSize', 11, 'FontWeight', 'bold');
xlabel('列', 'FontSize', 10);
ylabel('行', 'FontSize', 10);
axis image;

% 子图5：环境地图
subplot(2,3,5);
% 绘制网格背景
imagesc(ones(grid_size));
colormap('gray');
hold on;

% 绘制障碍物（黑色）
for obs_idx = 1:size(obstacles, 1)
    rectangle('Position', [obstacles(obs_idx,2)-1, obstacles(obs_idx,1)-1, 1, 1], ...
        'FaceColor', [0.2,0.2,0.2], 'EdgeColor', 'black', 'LineWidth', 1);
end

% 绘制起点和终点
plot(start(2)-0.5, start(1)-0.5, '^', 'MarkerFaceColor', 'red', 'MarkerEdgeColor', 'black', 'MarkerSize', 15);
plot(goal(2)-0.5, goal(1)-0.5, 'pentagram', 'MarkerFaceColor', 'yellow', 'MarkerEdgeColor', 'black', 'MarkerSize', 20);

% 绘制最优路径
if ~isempty(optimal_path)
    path_x = zeros(1, length(optimal_path));
    path_y = zeros(1, length(optimal_path));
    for idx = 1:length(optimal_path)
        path_x(idx) = optimal_path{idx}(2)-0.5;
        path_y(idx) = optimal_path{idx}(1)-0.5;
    end
    plot(path_x, path_y, 'b-', 'LineWidth', 3);
    plot(path_x, path_y, 'bo', 'MarkerSize', 6, 'MarkerFaceColor', 'b');
end

% 添加网格线
for i = 0:grid_size(1)
    plot([0, grid_size(2)], [i, i], 'k-', 'LineWidth', 0.5);
end
for j = 0:grid_size(2)
    plot([j, j], [0, grid_size(1)], 'k-', 'LineWidth', 0.5);
end

xlim([-0.5, grid_size(2)+0.5]);
ylim([-0.5, grid_size(1)+0.5]);
set(gca, 'XTick', 1:grid_size(2), 'YTick', 1:grid_size(1));
xlabel('列', 'FontSize', 10);
ylabel('行', 'FontSize', 10);
title('复杂迷宫环境与最优路径', 'FontSize', 11, 'FontWeight', 'bold');
hold off;
axis equal;

% 子图6：训练统计
subplot(2,3,6);
stats_text = sprintf(['训练统计信息：\n' ...
                      '网格大小: %d×%d\n' ...
                      '障碍数量: %d\n' ...
                      '训练回合: %d\n' ...
                      '训练时间: %.1f秒\n' ...
                      '平均奖励: %.2f\n' ...
                      '最终成功率: %.1f%%\n' ...
                      '路径长度: %d步'], ...
                      grid_size(1), grid_size(2), ...
                      size(obstacles,1), ...
                      num_episodes, ...
                      training_time, ...
                      mean(reward_history(end-100:end)), ...
                      mean(success_rate(end-100:end))*100, ...
                      length(optimal_path));
text(0.1, 0.5, stats_text, 'FontSize', 10, 'VerticalAlignment', 'middle');
axis off;
title('训练结果统计', 'FontSize', 11, 'FontWeight', 'bold');

sgtitle('复杂环境MDP路径规划仿真', 'FontSize', 14, 'FontWeight', 'bold');

%% 4. 显示详细结果
fprintf('\n=== MDP复杂环境路径规划结果 ===\n');
fprintf('网格大小: %d × %d\n', grid_size(1), grid_size(2));
fprintf('障碍数量: %d\n', size(obstacles,1));
fprintf('目标位置: 第%d行, 第%d列\n', goal(1), goal(2));
fprintf('起点位置: 第%d行, 第%d列\n', start(1), start(2));
fprintf('训练时间: %.2f 秒\n', training_time);
fprintf('训练回合: %d\n', num_episodes);
fprintf('最终平均奖励: %.2f\n', mean(reward_history(end-100:end)));
fprintf('最终成功率: %.1f%%\n', mean(success_rate(end-100:end))*100);

fprintf('\n最优路径 (%d步):\n', length(optimal_path));
if length(optimal_path) <= 20
    for i = 1:length(optimal_path)
        fprintf('第%2d步: (行%d, 列%d)\n', i, optimal_path{i}(1), optimal_path{i}(2));
    end
else
    fprintf('路径太长，显示前10步和后10步：\n');
    for i = 1:10
        fprintf('第%2d步: (行%d, 列%d)\n', i, optimal_path{i}(1), optimal_path{i}(2));
    end
    fprintf('... 省略中间 %d 步 ...\n', length(optimal_path)-20);
    for i = length(optimal_path)-9:length(optimal_path)
        fprintf('第%2d步: (行%d, 列%d)\n', i, optimal_path{i}(1), optimal_path{i}(2));
    end
end

%% 增强的Q-Learning算法（处理多个障碍物）
function [Q_table, reward_history, success_rate] = mdp_q_learning_enhanced(grid_size, num_states, num_actions, R, obstacles, goal, alpha, gamma, epsilon, num_episodes, max_steps)
    % 增强的Q-Learning算法实现
    % 初始化Q表
    Q_table = zeros(num_states, num_actions);
    
    % 历史记录
    reward_history = zeros(num_episodes, 1);
    success_rate = zeros(num_episodes, 1);
    
    % 目标状态
    goal_state = goal(1)-1 + (goal(2)-1)*grid_size(1);
    
    % 障碍状态集合
    obstacle_states = [];
    for obs_idx = 1:size(obstacles, 1)
        obstacle_state = obstacles(obs_idx,1)-1 + (obstacles(obs_idx,2)-1)*grid_size(1);
        obstacle_states = [obstacle_states, obstacle_state];
    end
    
    % 进度显示
    fprintf('训练进度: ');
    
    for episode = 1:num_episodes
        % 显示进度
        if mod(episode, num_episodes/10) == 0
            fprintf('%d%% ', round(episode/num_episodes*100));
        end
        
        % 随机选择起点（避开障碍和目标）
        while true
            start_row = randi(grid_size(1));
            start_col = randi(grid_size(2));
            state = start_row-1 + (start_col-1)*grid_size(1);
            if ~ismember(state, [goal_state, obstacle_states])
                break;
            end
        end
        
        current_state = state;
        total_reward = 0;
        steps = 0;
        success = 0;
        
        while steps < max_steps
            % ε-greedy策略选择动作（动态epsilon）
            current_epsilon = epsilon * (1 - episode/num_episodes);  % 随训练减少探索
            if rand() < current_epsilon
                % 探索：随机选择动作
                action = randi(num_actions);
            else
                % 利用：选择Q值最大的动作
                [~, action] = max(Q_table(current_state+1, :));
            end
            
            % 执行动作，得到下一个状态
            [next_state, valid_move] = take_action_enhanced(current_state, action, grid_size, obstacle_states);
            
            % 获取奖励
            if next_state == goal_state
                reward = 100 + (max_steps - steps) * 0.5;  % 越快到达奖励越高
                success = 1;
            elseif ismember(next_state, obstacle_states)
                reward = -50;
            elseif ~valid_move
                reward = -20;  % 撞墙惩罚
            else
                reward = -1;   % 正常移动
            end
            
            % Q-Learning更新公式
            current_Q = Q_table(current_state+1, action);
            max_next_Q = max(Q_table(next_state+1, :));
            Q_table(current_state+1, action) = current_Q + alpha * (reward + gamma * max_next_Q - current_Q);
            
            % 更新状态和奖励
            current_state = next_state;
            total_reward = total_reward + reward;
            steps = steps + 1;
            
            % 检查是否到达目标或障碍
            if next_state == goal_state || ismember(next_state, obstacle_states)
                break;
            end
        end
        
        % 记录历史
        reward_history(episode) = total_reward;
        success_rate(episode) = success;
    end
    fprintf('\n');
end

%% 增强的执行动作函数
function [next_state, valid_move] = take_action_enhanced(current_state, action, grid_size, obstacle_states)
    % 将状态索引转换为行列坐标
    row = mod(current_state, grid_size(1));
    col = floor(current_state / grid_size(1));
    
    valid_move = true;
    
    % 根据动作移动
    switch action
        case 1  % 上
            if row > 0
                row = row - 1;
            else
                valid_move = false;
            end
        case 2  % 下
            if row < grid_size(1)-1
                row = row + 1;
            else
                valid_move = false;
            end
        case 3  % 左
            if col > 0
                col = col - 1;
            else
                valid_move = false;
            end
        case 4  % 右
            if col < grid_size(2)-1
                col = col + 1;
            else
                valid_move = false;
            end
    end
    
    if valid_move
        next_state = row + col * grid_size(1);
        % 如果下一个状态是障碍，则保持原地
        if ismember(next_state, obstacle_states)
            valid_move = false;
            next_state = current_state;
        end
    else
        next_state = current_state;
    end
end

%% 增强的路径生成函数
function optimal_path = mdp_generate_optimal_path_enhanced(optimal_policy, start, goal, obstacles, grid_size)
    % 增强的路径生成函数
    optimal_path = {};
    current_pos = start;
    max_steps = 200;  % 防止无限循环
    
    step_count = 0;
    optimal_path{1} = current_pos;
    
    visited_positions = [current_pos];  % 存储已访问的位置
    
    while ~isequal(current_pos, goal) && step_count < max_steps
        step_count = step_count + 1;
        
        % 获取当前位置的最优动作
        action = optimal_policy(current_pos(1), current_pos(2));
        
        % 如果遇到障碍或无效动作，尝试次优动作
        if action == -1 || step_count > max_steps*0.8
            % 寻找可用的移动方向
            possible_moves = [];
            % 检查四个方向
            if current_pos(1) > 1
                next_pos = [current_pos(1)-1, current_pos(2)];
                if ~is_obstacle(next_pos, obstacles)
                    possible_moves = [possible_moves; 1];
                end
            end
            if current_pos(1) < grid_size(1)
                next_pos = [current_pos(1)+1, current_pos(2)];
                if ~is_obstacle(next_pos, obstacles)
                    possible_moves = [possible_moves; 2];
                end
            end
            if current_pos(2) > 1
                next_pos = [current_pos(1), current_pos(2)-1];
                if ~is_obstacle(next_pos, obstacles)
                    possible_moves = [possible_moves; 3];
                end
            end
            if current_pos(2) < grid_size(2)
                next_pos = [current_pos(1), current_pos(2)+1];
                if ~is_obstacle(next_pos, obstacles)
                    possible_moves = [possible_moves; 4];
                end
            end
            
            if ~isempty(possible_moves)
                % 随机选择一个可用方向
                action = possible_moves(randi(length(possible_moves)));
            else
                fprintf('无可用移动方向，路径终止。\n');
                break;
            end
        end
        
        % 执行动作
        next_pos = current_pos;
        switch action
            case 1  % 上
                next_pos(1) = current_pos(1) - 1;
            case 2  % 下
                next_pos(1) = current_pos(1) + 1;
            case 3  % 左
                next_pos(2) = current_pos(2) - 1;
            case 4  % 右
                next_pos(2) = current_pos(2) + 1;
        end
        
        % 检查是否碰到障碍
        if is_obstacle(next_pos, obstacles)
            fprintf('警告：路径碰到障碍物！\n');
            break;
        end
        
        % 检查是否在原地踏步
        if isequal(next_pos, current_pos)
            fprintf('警告：路径无法继续前进！\n');
            break;
        end
        
        % 检查是否回到已经访问过的位置
        visited = false;
        for i = 1:size(visited_positions, 1)
            if isequal(next_pos, visited_positions(i, :))
                visited = true;
                break;
            end
        end
        
        if visited && step_count > 5
            fprintf('警告：检测到循环路径！\n');
            break;
        end
        
        current_pos = next_pos;
        optimal_path{end+1} = current_pos;
        visited_positions = [visited_positions; current_pos];  % 添加到已访问列表
    end
    
    % 如果成功到达目标
    if isequal(current_pos, goal)
        fprintf('成功找到从起点到终点的路径！\n');
    else
        fprintf('未能到达目标位置，停在 (行%d, 列%d)。\n', current_pos(1), current_pos(2));
    end
end

%% 辅助函数：检查是否为障碍
function result = is_obstacle(position, obstacles)
    result = false;
    for i = 1:size(obstacles, 1)
        if isequal(position, obstacles(i, :))
            result = true;
            return;
        end
    end
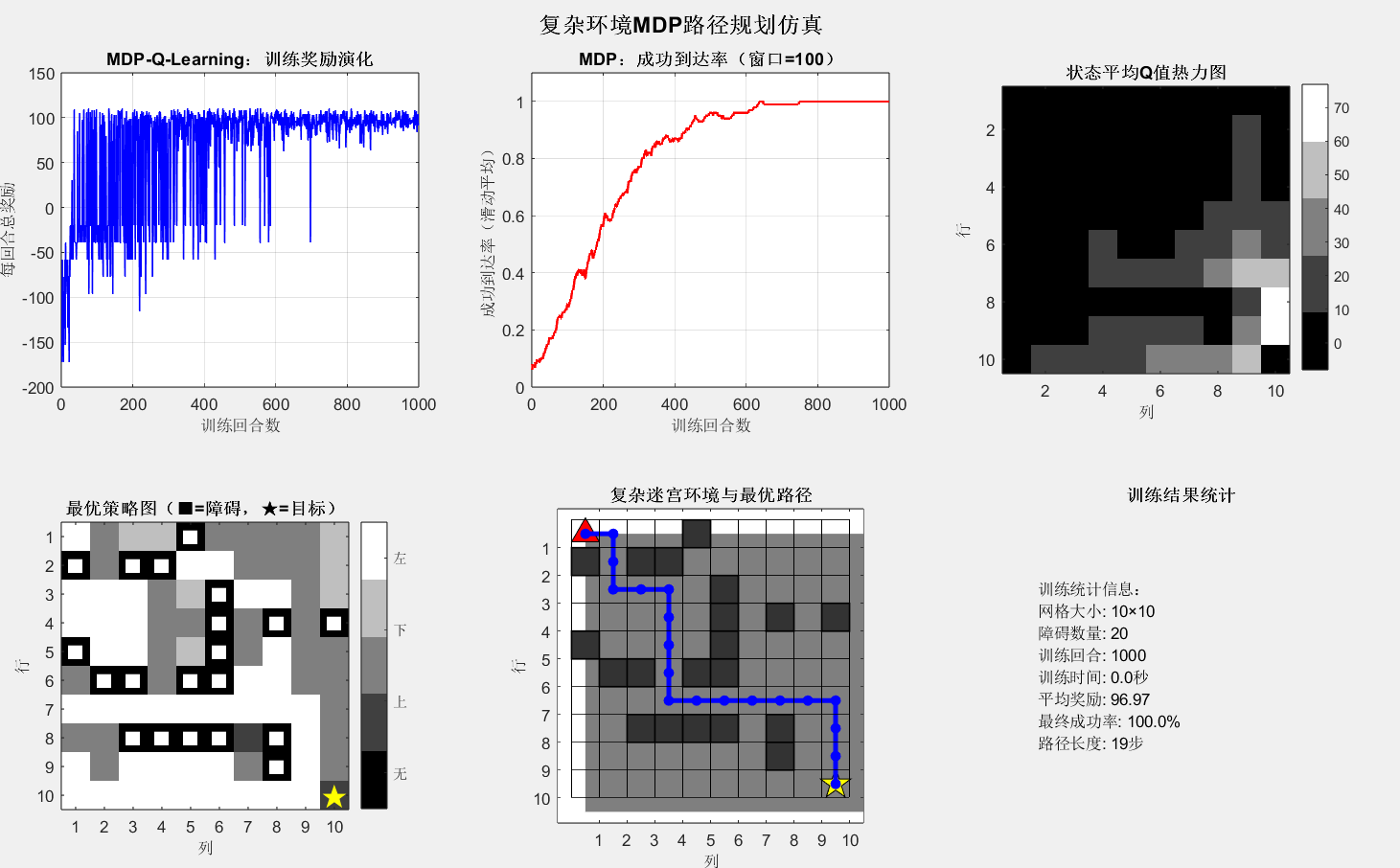
end

开始训练...

训练进度: 10% 20% 30% 40% 50% 60% 70% 80% 90% 100%

训练完成！用时 0.05 秒

生成最优路径...

成功找到从起点到终点的路径！

=== MDP复杂环境路径规划结果 ===

网格大小: 10 × 10

障碍数量: 20

目标位置: 第10行, 第10列

起点位置: 第1行, 第1列

训练时间: 0.05 秒

训练回合: 1000

最终平均奖励: 96.97

最终成功率: 100.0%

最优路径 (19步):

第 1步: (行1, 列1)

第 2步: (行1, 列2)

第 3步: (行2, 列2)

第 4步: (行3, 列2)

第 5步: (行3, 列3)

第 6步: (行3, 列4)

第 7步: (行4, 列4)

第 8步: (行5, 列4)

第 9步: (行6, 列4)

第10步: (行7, 列4)

第11步: (行7, 列5)

第12步: (行7, 列6)

第13步: (行7, 列7)

第14步: (行7, 列8)

第15步: (行7, 列9)

第16步: (行7, 列10)

第17步: (行8, 列10)

第18步: (行9, 列10)

第19步: (行10, 列10)

相关推荐
阿正的梦工坊1 小时前
Git Rebase 是什么？为什么需要它？
人工智能·git
檐下翻书1731 小时前
法律文书自动生成与逻辑校验
人工智能
源代码•宸1 小时前
GoLang八股（Go语言基础）
开发语言·后端·golang·map·defer·recover·panic
de之梦-御风1 小时前
【深度学习】模型从训练完成到产线运行的完整使用方式
人工智能·深度学习
rit84324991 小时前
基于MATLAB的SUSAN特征检测算子边缘提取实现
开发语言·matlab
g***55751 小时前
Java高级开发进阶教程之系列
java·开发语言
Java后端的Ai之路1 小时前
【人工智能领域】-YOLO目标检测算法全解析（含大白话解释）
人工智能·yolo·目标检测·cnn
鲁正杰1 小时前
【运维部署】现代化内网穿透与文件共享方案 (Rust)
运维·开发语言·rust
百家方案1 小时前
“十五五”智慧城市解决方案：从技术赋能到场景智治，再造城市生命共同体
人工智能·智慧城市
_codemonster1 小时前
深度学习实战（基于pytroch）系列完整目录
人工智能·深度学习
热门推荐
01GitHub 镜像站点02Labelme从安装到标注：零基础完整指南03安娜的档案(Anna’s Archive) 镜像网站/国内最新可访问入口（持续更新）04Linux下V2Ray安装配置指南05手把手教你通过Gemini3 pro 学生认证，白用一年，手慢无！06【踩坑笔记】50系显卡适配的 PyTorch 安装07GitLab 零基础入门指南：从安装到项目管理全流程08jdk21下载、安装（Windows、Linux、macOS）09UV安装并设置国内源102025-04-03 Latex学习1——本地配置Latex + VScode环境