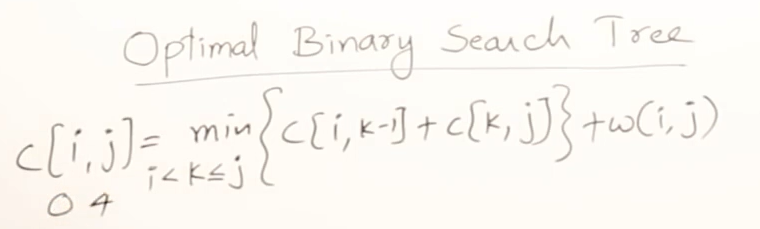目录
- 动态规划
-
-
- [1. 两大核心前提](#1. 两大核心前提)
- [2. 两种基本实现方式](#2. 两种基本实现方式)
- [3. 解题的关键步骤](#3. 解题的关键步骤)
- [4. 典型应用场景](#4. 典型应用场景)
-
- 算法实现
动态规划
动态规划(Dynamic Programming, DP)是一种通过拆分问题、存储子问题答案来解决复杂问题的优化算法,核心是避免重复计算。
1. 两大核心前提
动态规划并非适用于所有问题,它的应用需要满足两个前提。
- 重叠子问题 :在解决主问题的过程中,会反复遇到相同的子问题。
- 例如计算斐波那契数列时,求
fib(5)需要fib(4)和fib(3),而求fib(4)又需要fib(3)和fib(2),fib(3)就被重复计算了。
- 例如计算斐波那契数列时,求
- 最优子结构 :主问题的最优解 可以由子问题的最优解 推导得出。
- 例如求从A到C的最短路径,若A→B→C是最优路径,那么A→B和B→C也必须分别是各自路段的最短路径。
2. 两种基本实现方式
根据存储子问题答案的方式不同,动态规划主要有两种实现思路。
| 实现方式 | 核心逻辑 | 优缺点 |
|---|---|---|
| 备忘录法(递归) | 从主问题出发,递归拆解成子问题,用"备忘录"(如数组、哈希表)存储已计算的子问题答案,遇到已算过的直接取用。 | 优点:只计算需要的子问题,节省空间; 缺点:递归可能导致栈溢出,效率略低于迭代。 |
| 动态规划表法(迭代) | 从最小的子问题开始,按顺序计算并存储答案(如用数组构建DP表),逐步推导到主问题。 | 优点:无栈溢出风险,效率高; 缺点:可能会计算一些主问题用不到的子问题,消耗更多空间。 |
3. 解题的关键步骤
- 定义状态 :明确DP表(或备忘录)中每个元素的含义,即"
dp[i]代表什么"。- 例如在"爬楼梯"问题中,
dp[i]可定义为"爬到第i级台阶的总方法数"。
- 例如在"爬楼梯"问题中,
- 推导状态转移方程 :找到子问题之间的关系,即如何通过
dp[i-1]、dp[i-2]等前序状态,计算出dp[i]。- 爬楼梯问题中,
dp[i] = dp[i-1] + dp[i-2](因为第i级台阶只能从第i-1级或i-2级爬上来)。
- 爬楼梯问题中,
- 确定初始条件 :给出最小子问题的答案,作为推导的起点。
- 爬楼梯问题中,
dp[1] = 1(1级台阶1种方法),dp[2] = 2(2级台阶2种方法)。
- 爬楼梯问题中,
- 计算最终结果 :根据初始条件和转移方程,逐步计算到目标状态(如
dp[n])。
4. 典型应用场景
动态规划常用于解决具有"多阶段决策"特征的问题,常见场景包括:
- 计数类:如爬楼梯(求方法数)、不同路径(求路径总数)。
- 最值类:如最长递增子序列(求最长长度)、最小路径和(求路径最小值)。
- 存在类:如分割等和子集(判断是否存在满足条件的子集)、单词拆分(判断字符串能否被拆分)。
算法实现
基于动态规划算法求解最优二叉搜索树问题
1)前置知识
二叉搜索树(Binary Search Tree, BST)是一种满足特定排序规则的二叉树,查询、插入、删除操作高效。
对于树中的任意一个节点,其左子树上所有节点的值都小于它本身的值,其右子树上所有节点的值都大于它本身的值。(左<根<右)
( 2 n ) ! n ! ⋅ ( n + 1 ) ! \frac{(2n)!}{n! \cdot (n+1)!} n!⋅(n+1)!(2n)!( 2 n C n n + 1 \frac{2n \mathrm{C}_n}{n+1} n+12nCn)是卡特兰数的经典表达式,用于计算有n个不同节点时,能构造的二叉搜索树的总数量。
2)视频及重点
3)状态转移方程
-
状态定义 :
dp[i][j]表示用关键字k_i, k_{i+1}, ..., k_j构建的最优二叉搜索树的最小期望代价 (i > j时表示空树,对应伪关键字d_{i-1})。 -
转移方程 :
对于区间
[i, j](i ≤ j),选择k(i ≤ k ≤ j)作为根节点,则:
d p [ i ] [ j ] = min i ≤ k ≤ j { d p [ i ] [ k − 1 ] + d p [ k + 1 ] [ j ] } + s u m ( i , j ) dp[i][j] = \min_{i \leq k \leq j} \left\{ dp[i][k-1] + dp[k+1][j] \right\} + sum(i, j) dp[i][j]=i≤k≤jmin{dp[i][k−1]+dp[k+1][j]}+sum(i,j)其中:
dp[i][k-1]是左子树(k_i到k_{k-1})的最小代价;dp[k+1][j]是右子树(k_{k+1}到k_j)的最小代价;sum(i, j)是区间[i, j]内所有关键字(k_i到k_j)和对应伪关键字的总权值和(因根节点的存在,左右子树所有节点的深度+1,总权值需累加一次)。
-
初始条件 :
当
i > j时(空树),dp[i][j] = q_{i-1}(q_{i-1}是伪关键字d_{i-1}的权值)。
4)代码(C++)
cpp
// 输出:
//
// 最优二叉搜索树的中序遍历: 10 20 30 40 50
// 最优二叉搜索树的先序遍历 : 20 10 50 40 30
#include <iostream>
#include <vector>
#include <climits> //提供各种基本数据类型的极限值(最大值、最小值)
using namespace std;
// 定义最优二叉搜索树节点结构
struct Node {
int key;
Node* left;
Node* right;
Node(int k) : key(k), left(nullptr), right(nullptr) {}
};
// 计算最优二叉搜索树并返回其根节点
Node* binarysearchtree(const vector<int>& keys, const vector<double>& probabilities) {
int n = keys.size();
if (n == 0) return nullptr;
// dp[i][j]表示由关键字i到j构成的最优二叉搜索树的最小代价
vector<vector<double>> dp(n + 2, vector<double>(n + 2, 0.0));
// root[i][j]记录关键字i到j构成的最优二叉搜索树的根节点索引
vector<vector<int>> root(n + 2, vector<int>(n + 2, 0));
// 前缀和数组,用于快速计算概率和
vector<double> prefixSum(n + 1, 0.0);
// 初始化前缀和
for (int i = 1; i <= n; ++i) {
prefixSum[i] = prefixSum[i - 1] + probabilities[i - 1];
}
// 单个节点的情况
for (int i = 1; i <= n; ++i) {
dp[i][i] = probabilities[i - 1];
root[i][i] = i;
}
// 处理长度为l的子序列,l从2到n
for (int l = 2; l <= n; ++l) {
// 子序列的起始位置i
for (int i = 1; i <= n - l + 1; ++i) {
int j = i + l - 1; // 子序列的结束位置j
dp[i][j] = INT_MAX;
double sum = prefixSum[j] - prefixSum[i - 1]; // 概率和
// 尝试以k为根节点
for (int k = i; k <= j; ++k) {
double current = sum;
if (k > i) current += dp[i][k - 1]; // 左子树代价
if (k < j) current += dp[k + 1][j]; // 右子树代价
// 更新最优解
if (current < dp[i][j]) {
dp[i][j] = current;
root[i][j] = k;
}
}
}
}
// 根据root数组构建最优二叉搜索树
auto buildTree = [&](auto& self, int i, int j) -> Node* {
if (i > j) return nullptr;
int k = root[i][j];
Node* node = new Node(keys[k - 1]); // keys是0索引,root是1索引
node->left = self(self, i, k - 1);
node->right = self(self, k + 1, j);
return node;
};
return buildTree(buildTree, 1, n);
}
// 中序遍历二叉树,验证是否为二叉搜索树
void inorderTraversal(Node* root) {
if (root == nullptr) return;
inorderTraversal(root->left);
cout << root->key << " ";
inorderTraversal(root->right);
}
// 先序遍历(展示树的结构:根->左->右)
void preorderTraversal(Node* root) {
if (root == nullptr) return;
cout << root->key << " ";
preorderTraversal(root->left);
preorderTraversal(root->right);
}
int main() {
// 关键字及其对应的概率
vector<int> keys = { 10, 20, 30, 40, 50 };
vector<double> probabilities = { 0.15, 0.30, 0.05, 0.20, 0.30 };
Node* root = binarysearchtree(keys, probabilities);
cout << "最优二叉搜索树的中序遍历: ";
inorderTraversal(root);
cout << endl;
cout << "最优二叉搜索树的先序遍历 : ";
preorderTraversal(root);
cout << endl;
// 释放内存
auto deleteTree = [](auto& self, Node* node) -> void {
if (node == nullptr) return;
self(self, node->left);
self(self, node->right);
delete node;
};
deleteTree(deleteTree, root);
return 0;
}算法思路:
- 定义dp[i][j]表示关键字ki到kj构成的最优二叉搜索树的最小代价
- 定义root[i][j]记录ki到kj构成的最优二叉搜索树的根节点
- 使用动态规划自底向上计算所有子问题的最优解
- 最后通过root数组回溯构建最优二叉搜索树结构
代码分析:
时间复杂度为O(n³),空间复杂度为O(n²)