1.螺旋矩阵
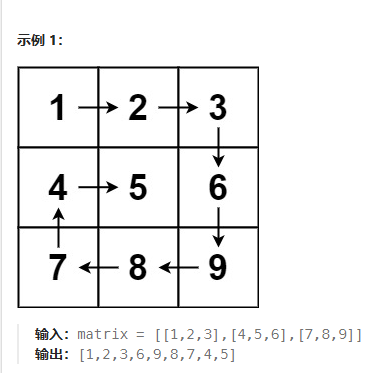
思路太夸张了
用DIRS = (0,1),(1,0),(0,-1),(-1,0)分别表示右下左上三个方向
i+=DIRS[di][0]
j+=DIRS[di][1]
di代表当前的方向di=0时对应的(0,1)i+0,j+1,说明向右走
di = (di+1)%4 右转
核心思路:先构造DIRS元祖,并且想到方向di
从i = 0 j = 0开始遍历
遍历到的做标记
额外引入x,y来做试探,判断是否走到边界,或者重复,这样说明要拐弯了
(如果直接用 i,j 操作,会导致 "移动后发现走不通,再回退" 的冗余逻辑)
i和j的变换逻辑和for循环不同,所以是新颖的赋值
i+=DIRS[di][0]
j+=DIRS[di][1]
时间复杂度 mn 空间复杂度 1
class Solution:
def spiralOrder(self, matrix: List[List[int]]) -> List[int]:
DIRS = (0,1),(1,0),(0,-1),(-1,0)#右下左上
i=j=di=0
m,n = len(matrix),len(matrix[0])
ans = []
for _ in range(m*n):
ans.append(matrix[i][j])
matrix[i][j] = None #标记表示走过
x,y = i+DIRS[di][0],j+DIRS[di][1]#试探步7777
if x<0 or y<0 or x==m or y==n or matrix[x][y] is None:
di = (di + 1) % 4
i+=DIRS[di][0]
j+=DIRS[di][1]
return ans2.旋转图像
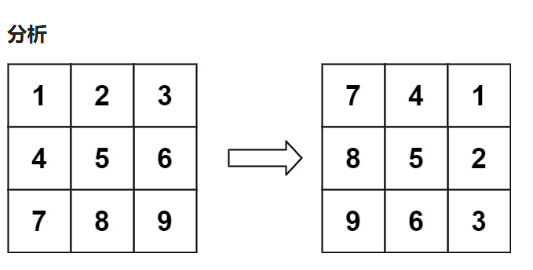
1.好理解的方法
先按对角线全部交换
然后每一行反转
这是线代的思路
转置+行翻转
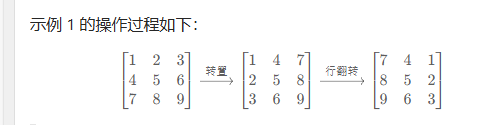
n方 1 但是两次循环
class Solution:
def rotate(self, matrix: List[List[int]]) -> None:
"""
Do not return anything, modify matrix in-place instead.
"""
n = len(matrix)
for i in range(n):
for j in range(i):
matrix[i][j],matrix[j][i] = matrix[j][i],matrix[i][j]
for row in matrix:
row.reverse()2.四角转换
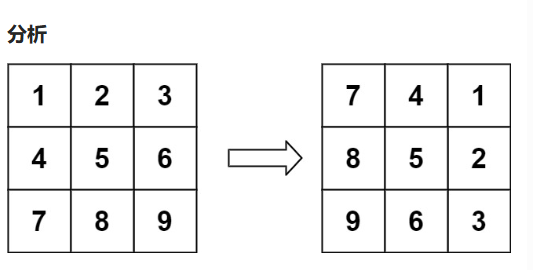
每个值都转了90°
核心逻辑:分层 + 四角交换
正方形矩阵旋转的本质是「按层旋转」,每层的元素通过「四个角循环交换」完成旋转:
四角的规律
i,j n-1-j,i n-1-i,n-1-j j,n-1-i
j i j
连接 连接 连接
外循环为了兼容奇数 / 偶数边长,即使出现奇数层,+1//2也能保证这层不用交换
内循环//2说实话没懂原理,死记硬背吧
n方 1 但是一次循环
class Solution:
def rotate(self, matrix: List[List[int]]) -> None:
"""
Do not return anything, modify matrix in-place instead.
"""
n = len(matrix)
for i in range((n+1)//2):
for j in range(n//2):
matrix[i][j],matrix[n-1-j][i],matrix[n-i-1][n-1-j],matrix[j][n-i-1]\
=matrix[n-1-j][i],matrix[n-i-1][n-1-j],matrix[j][n-i-1],matrix[i][j]