摘要:摘要:针对极端高温天气下电缆型配电网故障率上升问题,本文提出了一套韧性提升策略。首先建立了综合考虑电缆线路绝缘老化和接头热应力的故障率模型,通过蒙特卡洛模拟生成典型故障场景;其次构建了包含防御力、恢复力和协同力的多维韧性评估指标体系;最后提出协同优化模型,整合短时停运降温、网络重构、分布式电源孤岛运行、应急发电车和抢修调度等措施。算例验证表明,该方法能有效降低网络损耗(最高减少38%),提升关键负荷恢复量(达正常状态的92%),实现快速供电恢复。研究为提升城市电网应对极端高温能力提供了理论支撑和实践指导。
1 研究背景
1.1 极端高温天气频发对电缆型配电网构成严重威胁
近年来全球极端高温天气频次增加,尤其是2022年四川等地因高温导致大规模停电,经济损失巨大。
城市配电网电缆化率不断提升 (核心区达95%以上),高温会导致电缆绝缘老化、接头"竹节"现象,故障率显著上升。
1.2 现有研究存在不足
现有研究虽在电缆故障建模、配电网韧性评估与提升方面有所进展,但缺乏对高温下电缆故障 特点与多种韧性提升措施 (如网络重构、分布式电源、移动应急发电车、抢修等)协同作用的系统性研究。
2 创新点
2.1 构建了综合考虑电缆线路与接头的高温故障率模型
分别建立了电缆线路绝缘老化模型和接头热应力模型,并结合蒙特卡洛模拟与信息熵筛选出典型群发性故障场景。
2.2 提出多维韧性评估指标体系
从防御力、恢复力、协同力三个维度,提出"电缆网络损耗""电缆线路抗灾贡献度""关键负荷恢复量"等量化指标,实现韧性水平的综合评价。
2.3 构建了协同优化韧性提升模型
将高温电缆处理措施(如短时停运降温)与供电恢复措施(如网络重构、DG孤岛、应急发电车、抢修调度)进行协同优化,建立多目标优化模型,实现快速恢复与最大范围供电。
3 极端高温下电缆元件故障率及场景生成
由高温导致的地下电缆故障中,约49%由电缆接头故障诱发,27%由电缆接头间的电缆线路故障引起。因此,对于地下电缆线路与电缆接头的故障率建模必不可少。
3.1 极端高温下电缆线路故障率建模
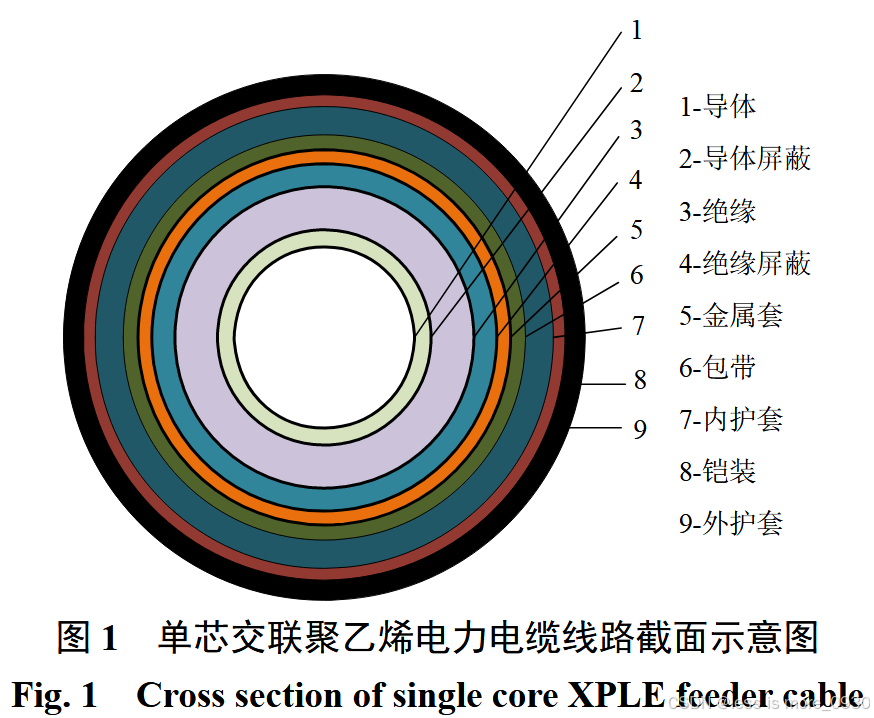
极端高温天气下,电缆线路所处环境温度高,且用电量大进一步加剧缆芯升温,缆芯升温加速绝缘部分老化损伤。电缆线路结构切面示意图如图1所示。
隧道敷设方式的电缆缆芯温度公式:
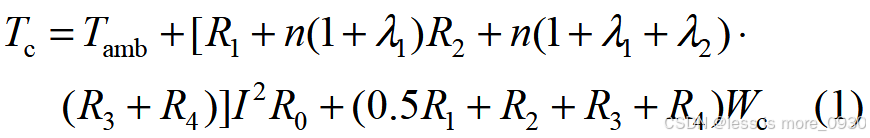
式中,Tc 为电缆缆芯运行温度(开氏温度,下同);Tamb 为电缆外部环境温度,与电缆敷设方式有关;n 为电缆数量;Wc 为单位长度电缆缆芯中产生的损耗,W/m;R 1、R 2、R 3、R 4 分别为单位长度电缆绝缘层、内护层、外护层以及电缆外部环境热阻,m⋅K/W;λ 1、λ 2 为金属屏蔽和铠装层损耗相对于电缆缆芯损耗比率;I 为电缆缆芯电流;R0 为电缆缆芯电阻。
采用综合运行时间与环境因素对电缆影响的威布尔比例风险模型评估电缆线路在电缆缆芯运行温度 Tc 下服役 t 小时后的可靠性:
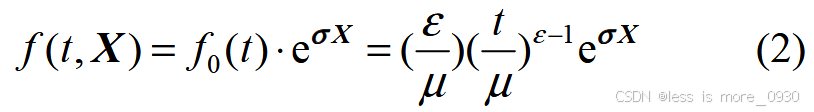
式中,f 0(t )为电缆基本故障率函数,仅与运行时间t 有关;ε 为电缆形状参数,可通过历史运行数据拟合得到;μ 为电缆特征寿命参数,可根据线路在额定温度下服役时间得到;X 为环境影响因素函数列矩阵[X 1,X 2,...,X 3]T,取实际电缆缆芯运行温度与缆芯额定温度的比值;σ 为X 的回归系数矩阵[σ 1,σ 2,...,σ3]T,可利用极大似然估计求得。
IEC60287 标准中,在交流系统下可利用电缆热路计算得到电缆绝缘温度:
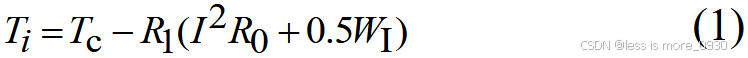
式中,Ti为电缆绝缘运行温度。
电缆线路绝缘寿命与电缆线路绝缘温度的关系服从 Arrhenius 定律:

式中,Li 为电缆绝缘寿命,h;A 为表观指前因子;E a为实验参数表观活化能;ξ为玻尔兹曼常数。
电缆绝缘运行在温度 Ti 下相对于其运行在额定温度下的老化速率为:
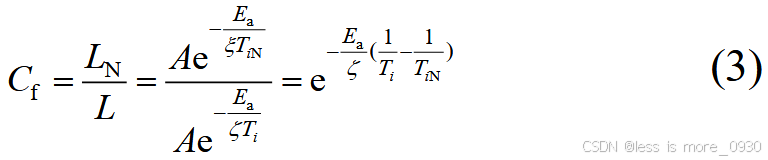
式中,C f 为电缆绝缘在运行温度下相对额定温度的老化速率;TiN 为电缆绝缘额定运行温度。
将地下电缆线路的总服役时间 t 均匀划分为 n 个时间段 ti ,可得服役时间 t 内相对于额定温度下总的绝缘寿命损失:

式中 L ie 为服役时间 t 内折算至额定运行温度下的绝缘寿命损失,h,L ie 即为式(2)中运行时间参数 t。
在等效绝缘寿命损失 L ie 和当前电缆缆芯运行温度 Tc 下电缆线路故障率计算模型:
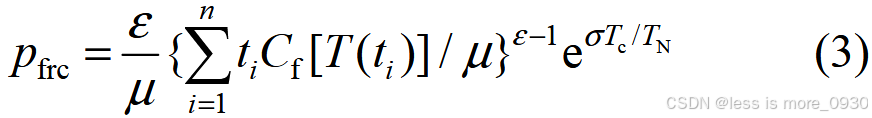
式中,P frc为电缆线路故障率;TN 为电缆缆芯额定运行温度。
3.2 极端高温下电缆接头故障率建模
极端高温天气,缆芯温度急剧上升,绝缘材料受热膨胀使电缆绝缘与接头附件间应力增大,压缩形变造成接头附近出现"竹节",增加接头损坏风险。
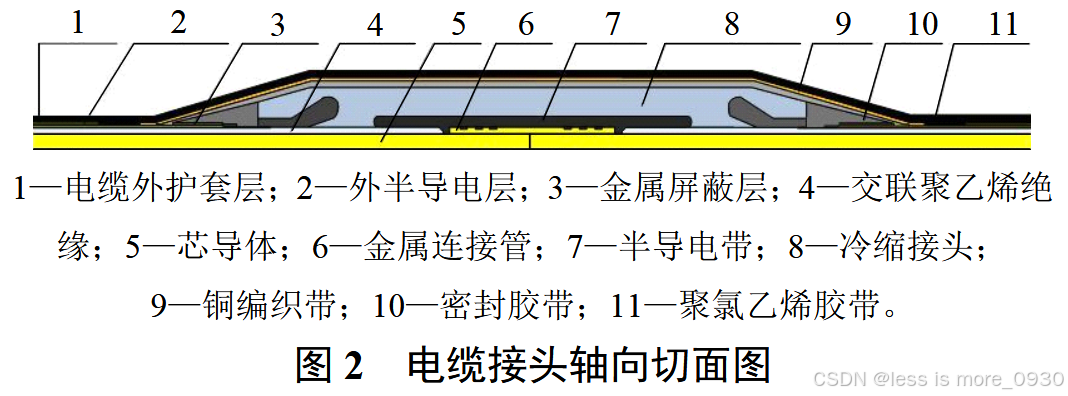
电缆屏蔽层很薄,忽略电磁影响简化计算。温度上升引起电缆绝缘层受热膨胀挤压电缆接头的应力采用如下张量方程组描述:
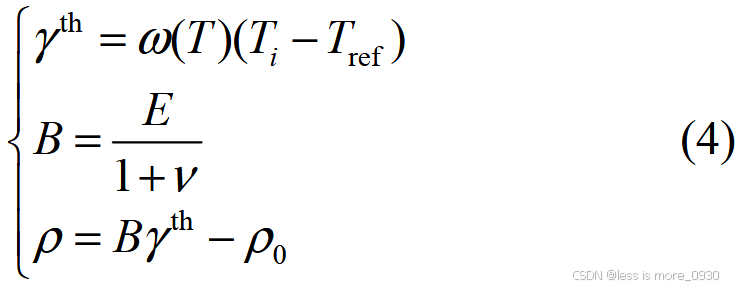
式中,γ th 为温度升高引起的热应变分量;ω 为热膨胀系数(×10−5K−1);B 为应变系数;T ref为电缆绝缘参考运行温度;E 为绝缘材料的弹性模量,Mpa;υ 为绝缘材料的泊松比;ρ 为应力张量;ρ0为界面应力张量的初始值。
假设电缆绝缘材料在不同温度、不同时间老化后的抗张强度服从正态分布,其抗张强度概率密度可表示为:
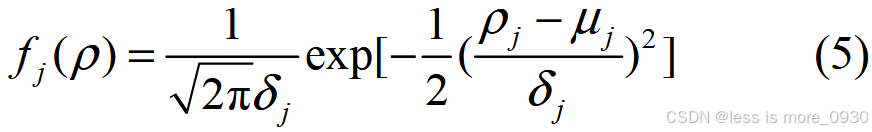
式中,fj (ρ )为电缆绝缘材料的抗张强度概率密度函数;ρj 为电缆接头所承受张力;δj 为绝缘材料抗张强度标准差;μj 为绝缘材料抗张强度均值;δj 与μj均可通过实验或实际运行经验获得。
当绝缘材料承受应力大于其抗张强度时,可认为绝缘材料被损坏,因此电缆接头故障率函数为:
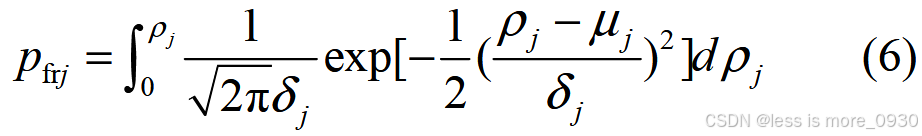
式中 P frj 为电缆接头 j 的故障率。
3.3 极端高温下电缆综合故障率计算及场景生成
电缆线路正常运行时电缆线路与电缆接头可视为串联模型,从而可推得在极端高温天气下电缆线路综合故障率为:
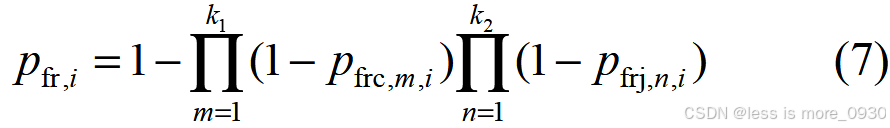
式中,p fr,i 为电缆线路 i 的故障率;k 1 为电缆线路 i 的电缆段数;k 2 为线路 i 的电缆接头个数;p frc,m ,i 、p frc,n ,i 分别为线路 i 第 m 段电缆线和第 n 个电缆接头的故障率。
信息熵约束:
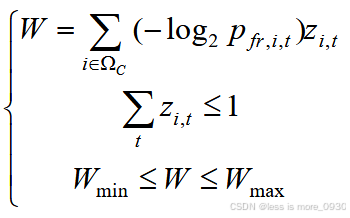
式中,W 为系统熵值;Ωc 为故障区负荷集合;p fr,i ,t 为线路 i 在时刻 t 的故障率;zi ,t 表示线路 i 在时刻 t 是否发生故障,取1故障,取0正常;W max、Wmin分别为系统熵值的上下限。
以电缆综合故障率为理论支撑,利用蒙特卡洛模拟并根据信息熵约束确定出具有随机性的极端高温天气下电缆群发性故障场景。由此筛选出的概率较低、故障影响较为严重的典型极端高温多重故障场景,可为灾后韧性提升策略研究提供场景支撑。
4 极端高温下电缆型配电网韧性提升模型
(1)暂时停运温度过高但未发生故障的电缆线路,并安排抢修小队降温;
(2)通过拓扑重构与DG孤岛恢复部分负荷,并利用移动式应急发电车为拓扑重构与DG孤岛无法恢复供电的区域提供电源支撑,从而最大范围保证受灾后电缆型配电网的快速电力供应,进而派遣抢修小队修复电缆型配电网的故障元件。
4.1 极端高温下电缆型配电网韧性提升措施及指标
结合韧性曲线,从防御力、恢复力和协同力3个层面,采用电缆线路降温降损、故障抢修和应急供电恢复组合策略等措施,提出电缆网络损耗、电缆线路抗灾贡献度、关键负荷恢复量等指标,量化分析极端高温灾害下电缆型配电网韧性水平。
1)利用电缆线路降温降损措施,并提出电缆网络损耗指标。
在极端高温天气出现后,暂时停运温度过高但未发生故障的电缆线路,并对其采取向电缆沟投放冰砖、向电缆井内喷水或送冷风等方式,为电缆线路降温。降温后线路满足最高长期工作温度,从而降低载流量,减少线路损耗。对应的电缆网络损耗计算公式如下:
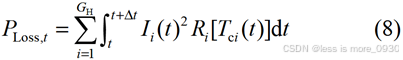
式中,P Loss,t 为t 时刻电缆型配电网络损耗;G H为采用电缆线路暂时停运降温措施后的网络电缆集合;Ii (t )为 t 时刻电缆 i 的电流;T ci (t )为 t 时刻电缆 i 缆芯温度;Ri [T ci (t )]为t 时刻电缆i 在T ci (t)温度下的电缆电阻。
2)基于故障抢修措施,建立电缆线路抗灾贡献度指标。
优先抢修电缆型配电网中承载功率高、能保持网架传输范围大的故障电缆线路,继而保障电缆型配电网在遭遇极端高温灾害后的传输能力与供电范围。对应的电缆线路抗灾贡献度指标计算公式:
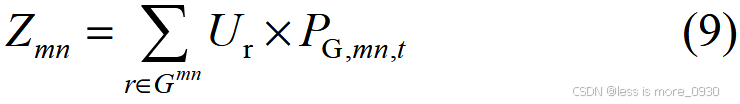
式中,Gmn 为恢复线路m -n 故障后的电网负荷集合;U r为抢修恢复线路m -n 后电网最大连通子图路径数;P G,mn ,t 为t 时刻电缆线路m -n传输功率。
3)基于受灾电缆线路应急恢复组合措施,建立关键负荷恢复量指标。
协同力是指电网协同内外部资源,在时间和空间维度最大限度为关键负荷供电的能力。极端高温天气下,通过利用计及DG的拓扑重构与孤岛供电措施、移动式应急发电车的灵活供电之间的协同机制,可提升电网在灾后协同多种资源恢复供电的能力,最大范围恢复电网供电。
持续高温对DG供电也有负面影响,光伏发电组件的理想工作温度25°C,气温升高1°C,发电量降低约0.35%。储能电站的电池组件最佳工作温度为25°C,温度升高10°C,放电功率降低0.5%。为保证光伏稳定出力,采用光伏与储能联合发电系统。
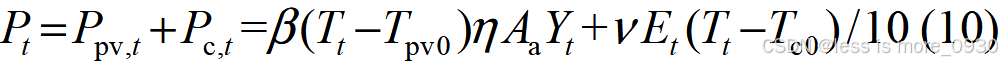
式中,Pt 为t 时刻光储联合发电总出力;P pv,t 为t 时刻修正后的光伏出力;P c,t 为t 时刻修正后的储能系统出力;η 为光电转换效率;β 为光伏出力下降系数;Aa 为光伏组织面积;Tt 为t 时刻气温;T pv0为光伏发电最佳温度;Yt 为t 时刻光照强度;ν 为储能出力下降系数;T c0为储能最佳工作温度;Et 为储能在t时刻放电功率。
综上所述,从协同力角度提出反映考虑重构、孤岛、移动式应急发电车协同恢复水平的关键负荷恢复量计算指标,可表示为:
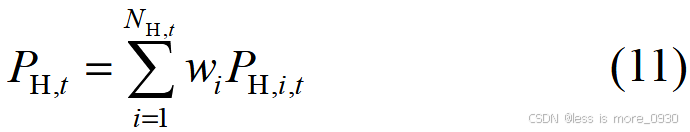
式中,P H,t 为t 时刻关键负荷恢复总量;N H,t 为实施抢修方案后t 时刻可恢复的负荷集合;ωi 为被恢复负荷i 的权重;P H,i ,t 为t 时刻下被恢复负荷i的有功功率。
4.2 目标函数
综合考虑电缆网络损耗、电缆线路抗灾贡献度、关键负荷恢复量综合最优,归一化处理得到目标函数为:
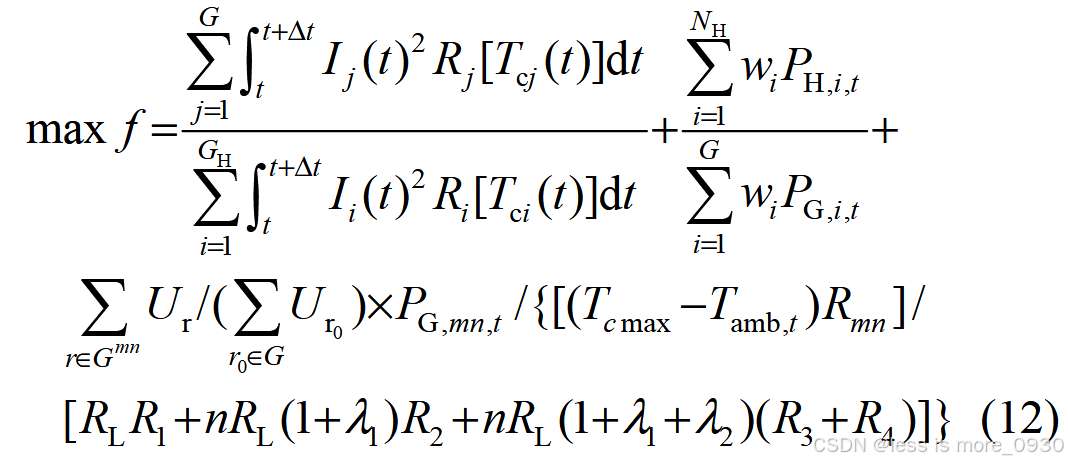
式中,G 为正常状态电网电缆集合;Ij (t )为t 时刻正常状态电缆线路流过的电流;Rj 为第j 条电缆电阻;P G,i ,t 为t 时刻下电网正常状态负荷有功功率;U r0为正常状态电网最大连通子图路径数量;Tc max为电缆最高允许长期工作温度;Rmn 为电缆m -n的电阻。
4.3 约束条件
(1)功率平衡、节点电压、拓扑及储能充放电约束
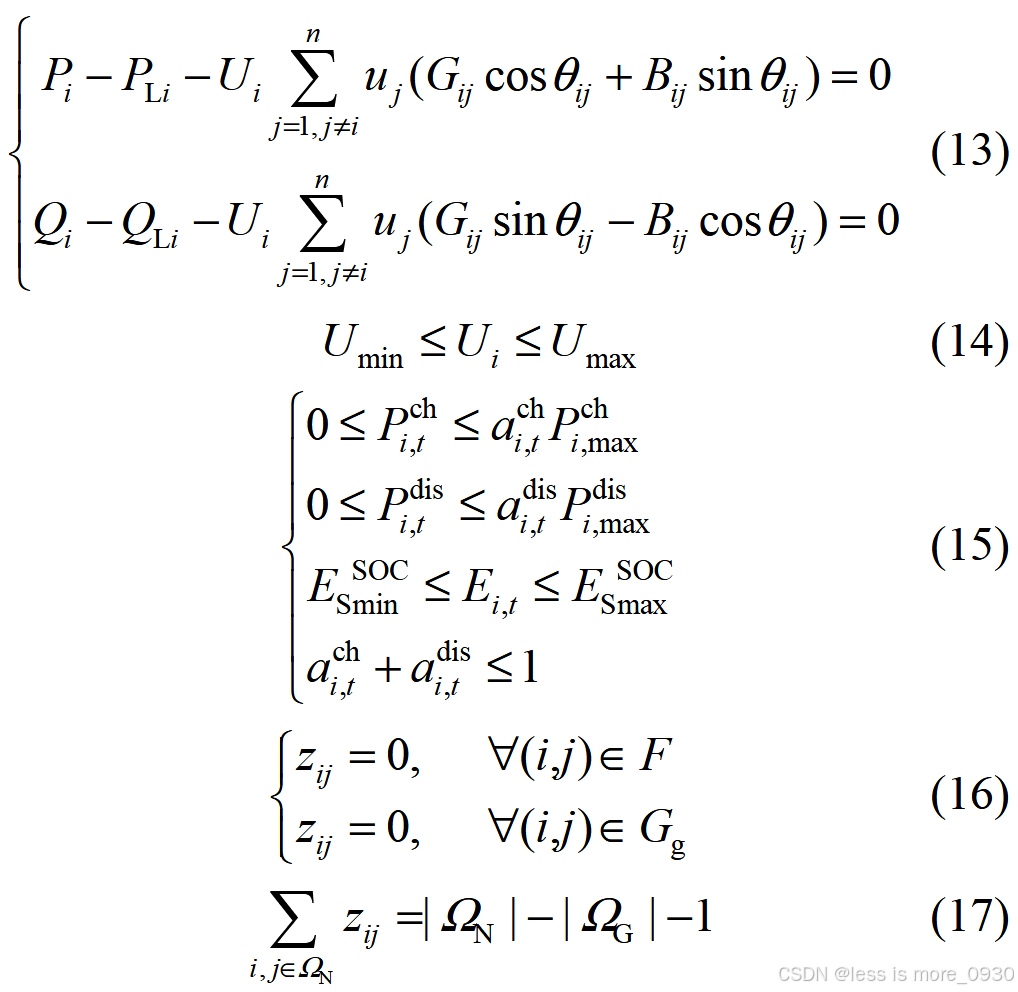
(2)为避免后续运行中因其余电缆温度过高而出现更多电缆故障,保证每条电缆线路工作在最高长期允许容量、电流之下,利用式(1)设置恢复后的电缆运行温度、容量、电流约束如下:
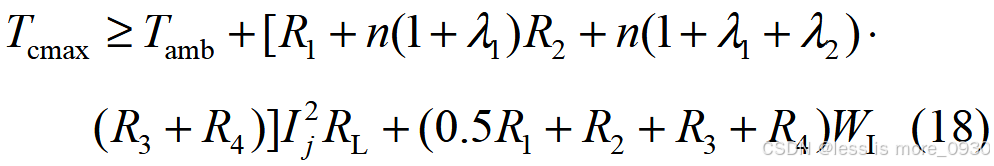
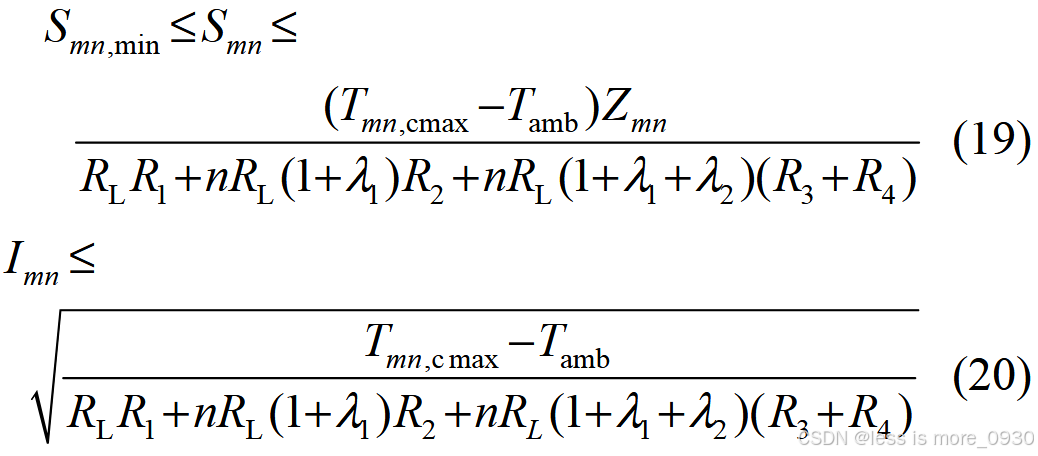
式中,Ij 为电缆j流过的电流;Smn 为支路m -n 的视在功率;Smn ,min为支路m -n 的视在功率下限;Tmn ,cmax为电缆m -n 最高长期允许工作温度;Imn 为电缆m -n的电流。
(3)孤岛内能量约束;孤岛拓扑约束,避免孤岛内出现环网。
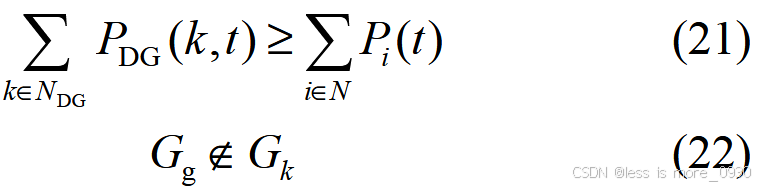
(4)抢修小队的调度与抢修过程中,规定故障元件仅由一组抢修小队修复,并且抢修小队都是从抢修中心出发,完成故障抢修任务后返回抢修中心。
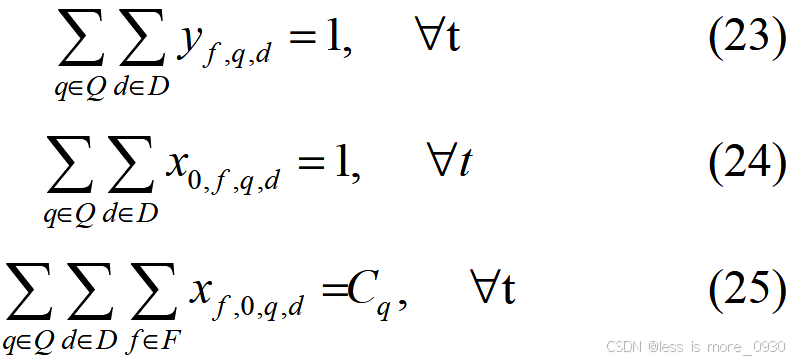
式中,Cq 为抢修中心个数;Q 为抢修中心集合;q 为抢修中心编号;D 为抢修中心中抢修小队集合;d 为抢修小队编号;f为故障电缆编号。
抢修时间约束包括抢修资源到达故障点所用时间、故障维修时长,不允许超过限值:
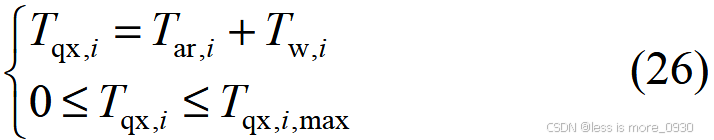
式中,T qx,i 为抢修故障电缆i 所用总时长;T ar,i 为抢修资源到达故障电缆i 所用时间;T w,i 为故障电缆i 的维修时长;T qx,i,max为电力部门规定抢修用时的最长时限。
(5)应急发电车的调度过程满足每台应急发电车只为一个节点供电,且每个节点只能由一辆应急发电车供电。同时,应急发电车在电量不足时需返回充电,充电完成后方可继续供电。
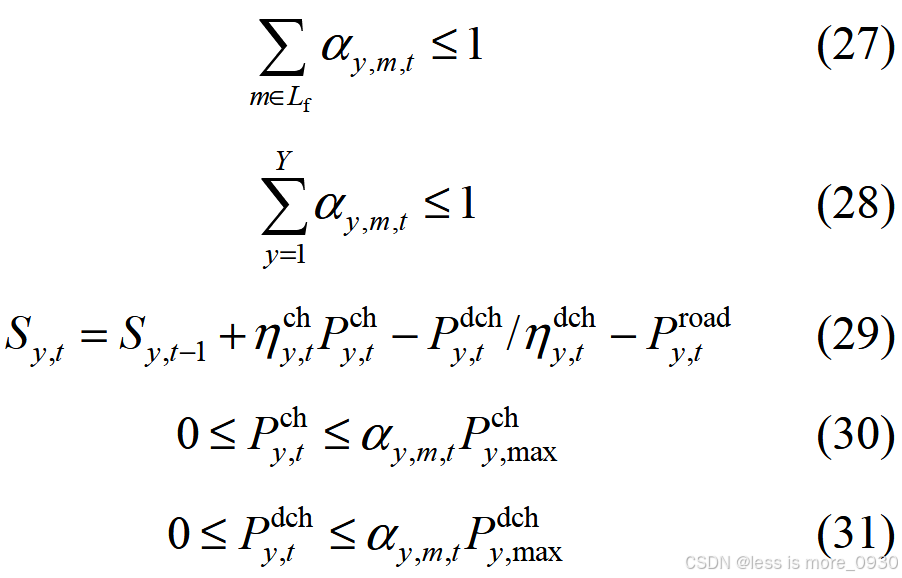
式中,Y 为应急发电车集合;y 为应急发电车编号;L f为失电负荷集合;m 为失电负荷编号;αy ,m ,t 为二进制变量,表示应急发电车y 是否为失电负荷m 充电,充电时取1;Sy ,t 、Sy ,t −1分别为t 、t −1时刻编号为y 的应急发电车的储能容量;P road y ,t 为t 时刻编号y应急发电车行驶耗电功率。
(6)为保证社会生产生活有序进行,t时刻故障后电缆型配电网负荷总恢复量必须达到正常状态下此时刻所有负荷量的90%以上。

式中,E f,t 为故障后t 时刻电缆型配电网负荷总恢复量;E N,t 为正常状态下t时刻电缆型配电网总负荷。
4.4 韧性提升流程
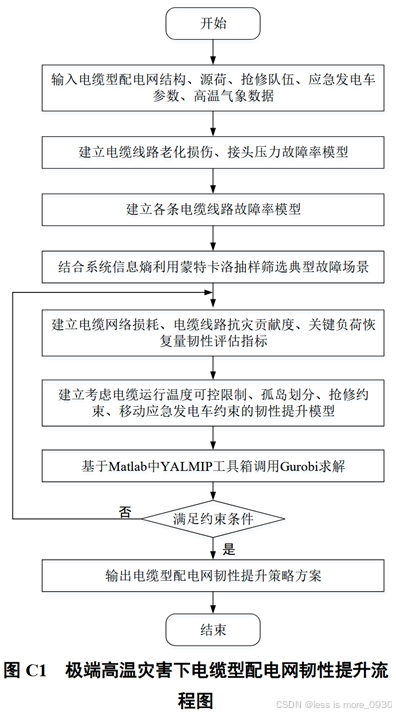
5 算例分析
5.1 算例概况
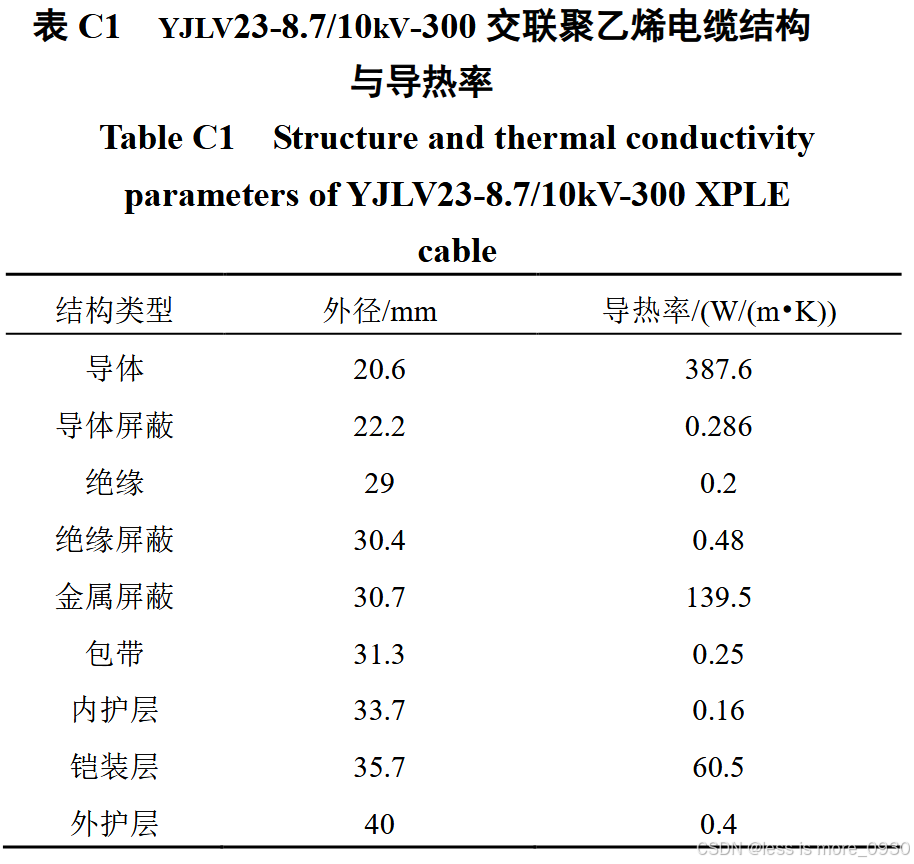
某特大城市核心区域的10kV电缆型配电网,共包含26个节点,25条电缆线路及1条联络线,所有电缆均为隧道铺设方式,埋深1m,电缆线路型号为YJLV23-8.7/10kV-300交联聚乙烯电缆,其具体结构参数如附表C1所示。
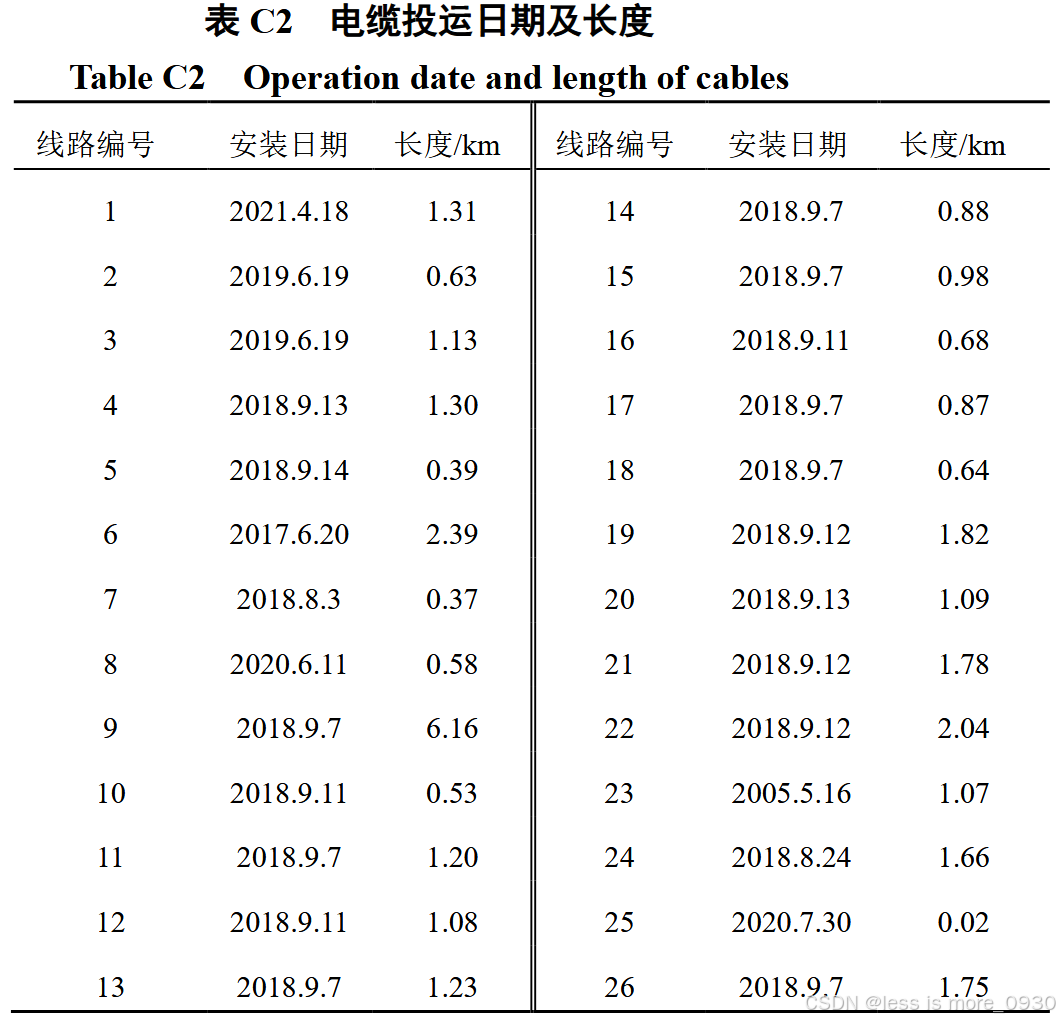
电缆铺设日期及长度均为实际数据,具体参见附表C2。
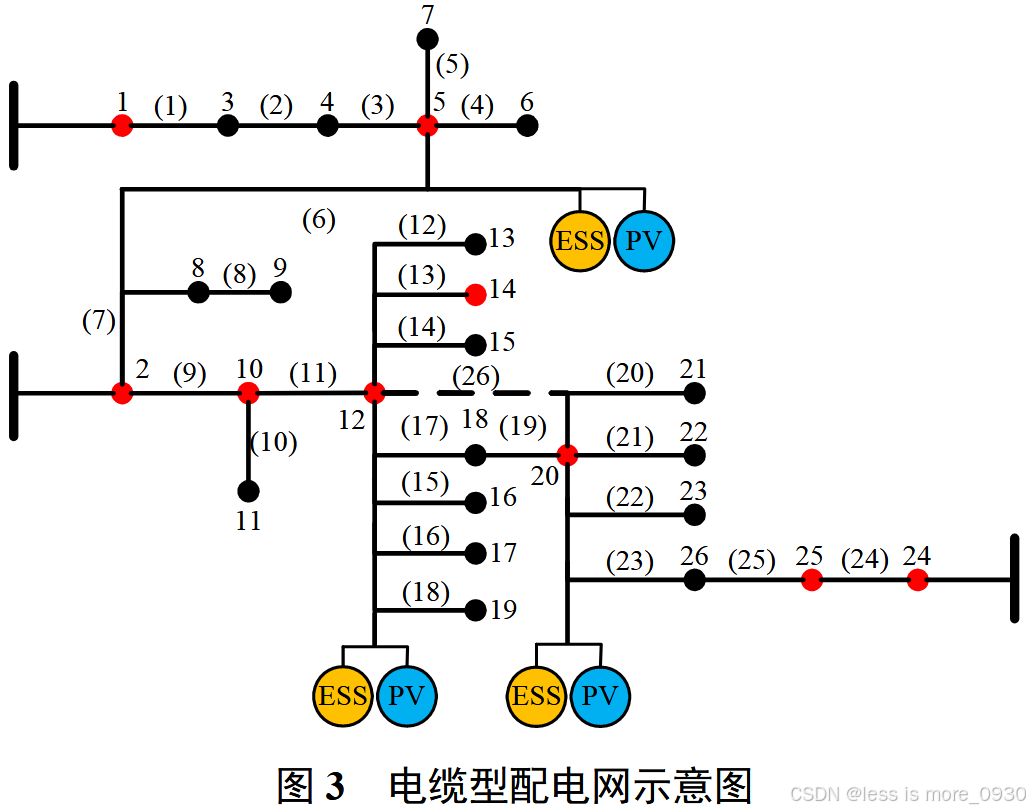
电缆线路每隔450m安装一个中间接头,在电缆线路两端均安装有终端接头。电缆型配电网拓扑示意图如图3所示。其中红色节点为关键负荷,黑色节点为普通负荷。
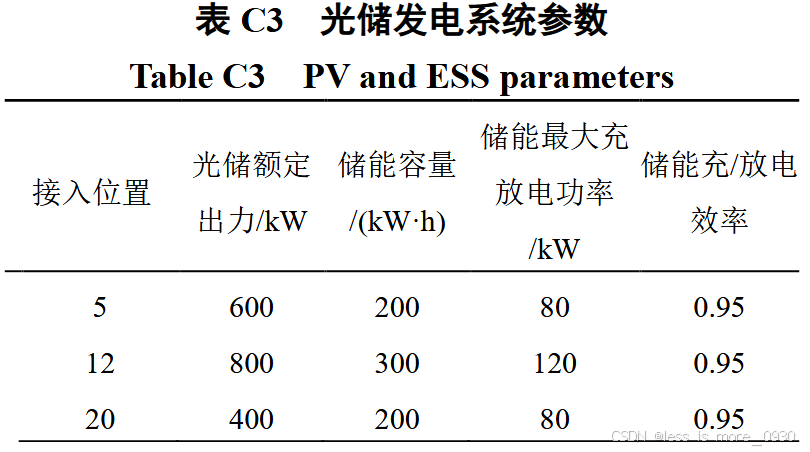
光储联合发电分别位于节点5、12、20,具体参见附表C3。
算例设定所在区域的1个抢修中心中有2支抢修小队,并且配备1台移动式应急发电车,应急发电车参数见附表C4。
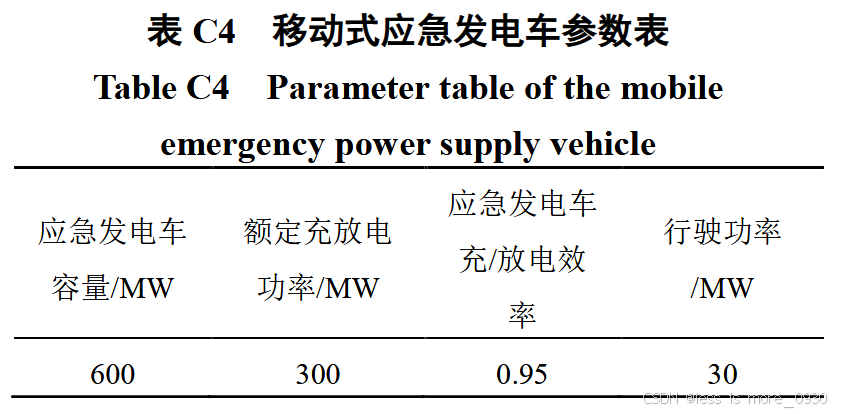
电缆型配电网所在区域面积不大,抢修小队与应急发电车在0.5h内均可从网络内任意一点达到另外一点。在实际高温电缆处理措施中,暂时停运的待降温线路从抢修小队到达至恢复供电需要0.5h,故障线路修复需要25.5h。因此,约束式(26)中暂时停运线路、故障线路T qx,i分别设置为1、26h。
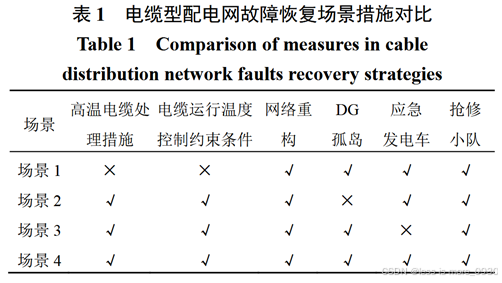
为验证本文所提的韧性提升组合策略的优越性,设置如下4个电缆型配电网故障恢复场景:
场景1:在所提电缆型配电网韧性提升优化模型中,不考虑高温电缆处理措施,且约束条件中不考虑电缆温度控制;
场景2:在所提电缆型配电网韧性提升优化模型中,不考虑DG孤岛运行措施;
场景3:在所提电缆型配电网韧性提升优化模型中,不考虑应急发电车措施;
场景4:利用式(12)---(32)的极端高温灾害下电缆型配电网韧性提升优化模型,统筹考虑极端高温下电缆短时停运降温措施与配电网抢修供电措施中的网络重构、孤岛运行、移动式应急发电车、抢修等措施。
以上4个场景中各故障恢复措施对比情况如表1所示。
5.2 电缆故障率计算及配电网复杂故障场景分析
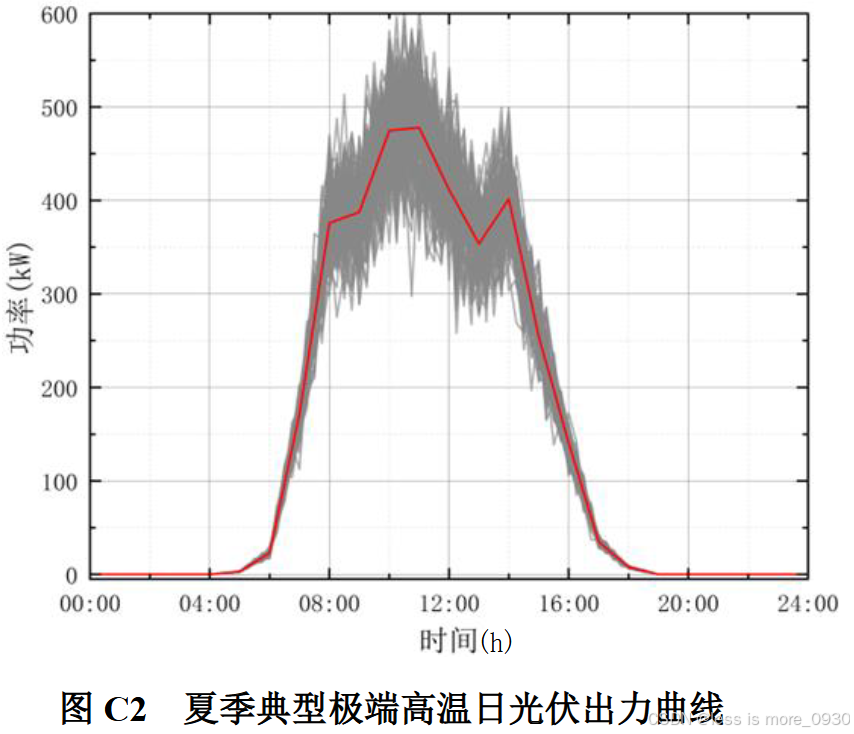
附图C2给出以夏季极端高温典型日DG出力为参考,通过蒙特卡洛抽样得到的DG出力曲线。
天气信息和电网负荷用电量采用配电网当地2022年夏季极端高温典型日的气温和负荷用电量,数据时间间隔为1h,在此期间假设温度和负荷恒定。
各时刻节点电压如附图C3所示。
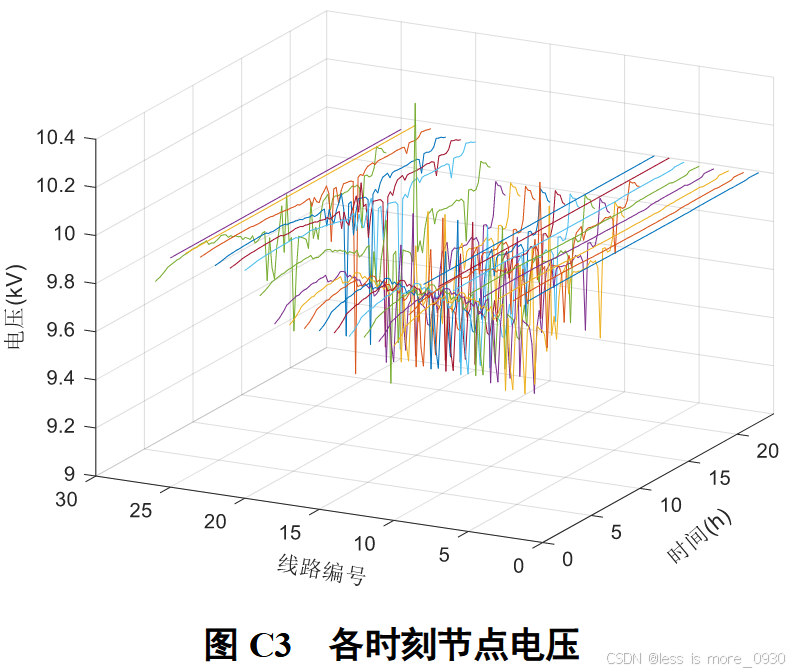
式(2)中电缆线路故障率模型特征寿命、形状参数和回归系数见附表C5。

式(4)电缆接头热压力模型中参数参见附表C6。

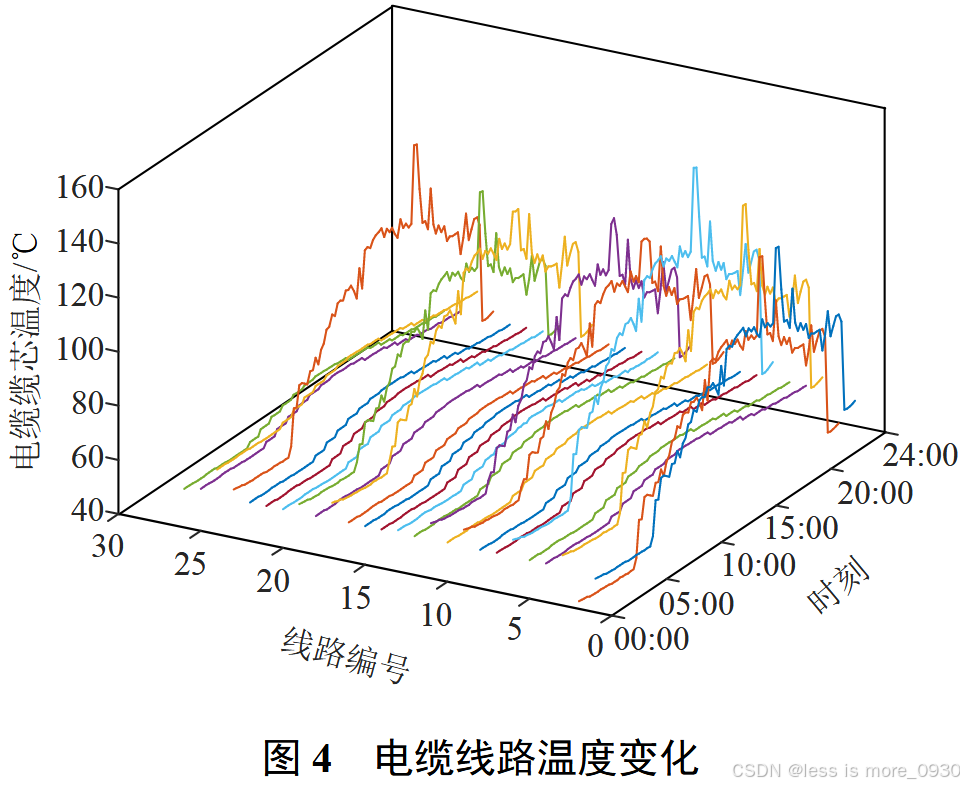
由式(1)计算出电缆未来24 h温度变化情况如图4所示。可以看出:
- 电缆线路整体从12:30开始升温,13:00---15:00处于极端高温,且用电量达到高峰时段,温度不断攀升,15:30温度达峰值,17:00后温度逐渐降至正常水平。
- 线路2、9、11、17在14:00---15:30存在某1h内温度达到120℃,但未达到最高短时(1h)允许工作温度130℃。线路19、23在14:00---15:30存在某1h内电缆温度达到130℃,需及时预防电缆损坏。线路3、6有2h温度达到145℃,极易发生故障。
- 以上高危电缆线路均是配电网中功率传输关键线路,载流量较大,因此在极端高温情况下电缆线路温度也会更高。
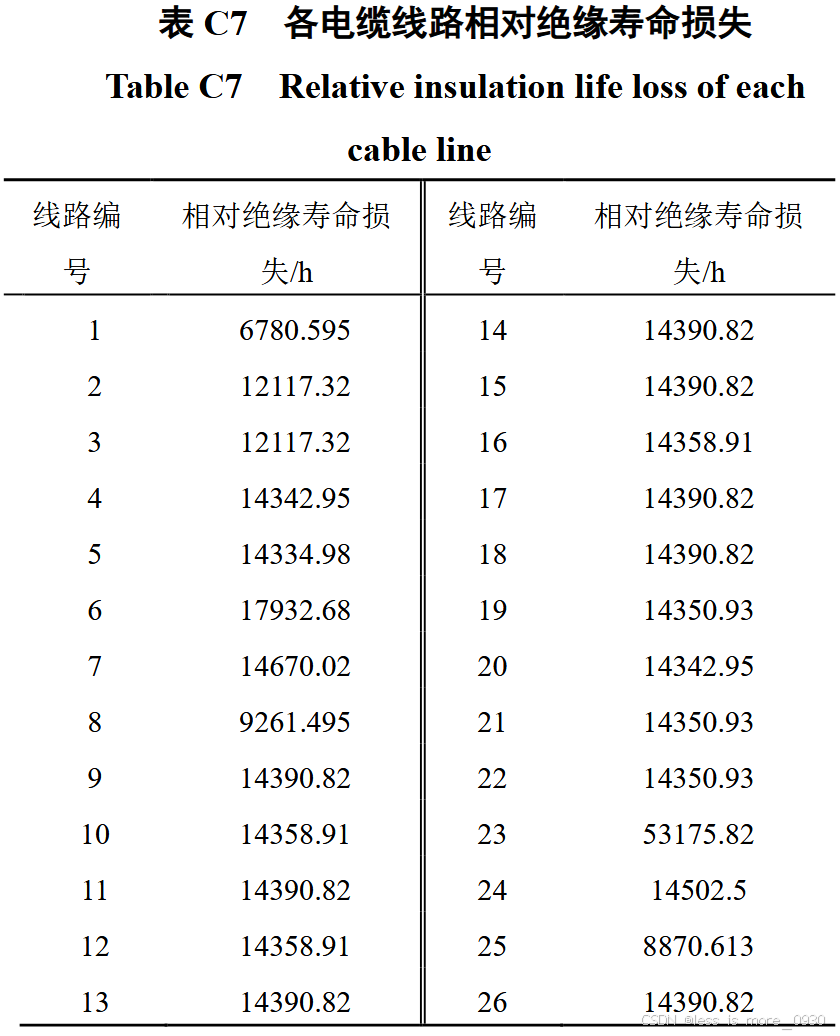
利用式(3)得到电缆线路未来 24 h 实时故障率如图 5 所示。相对绝缘寿命参见附表 C7。由图 5 可知,电缆线路的时变故障率最大时刻与极端高温峰值时刻一致。电缆线路故障率较高的线路也与缆芯温度较高的线路相符合。
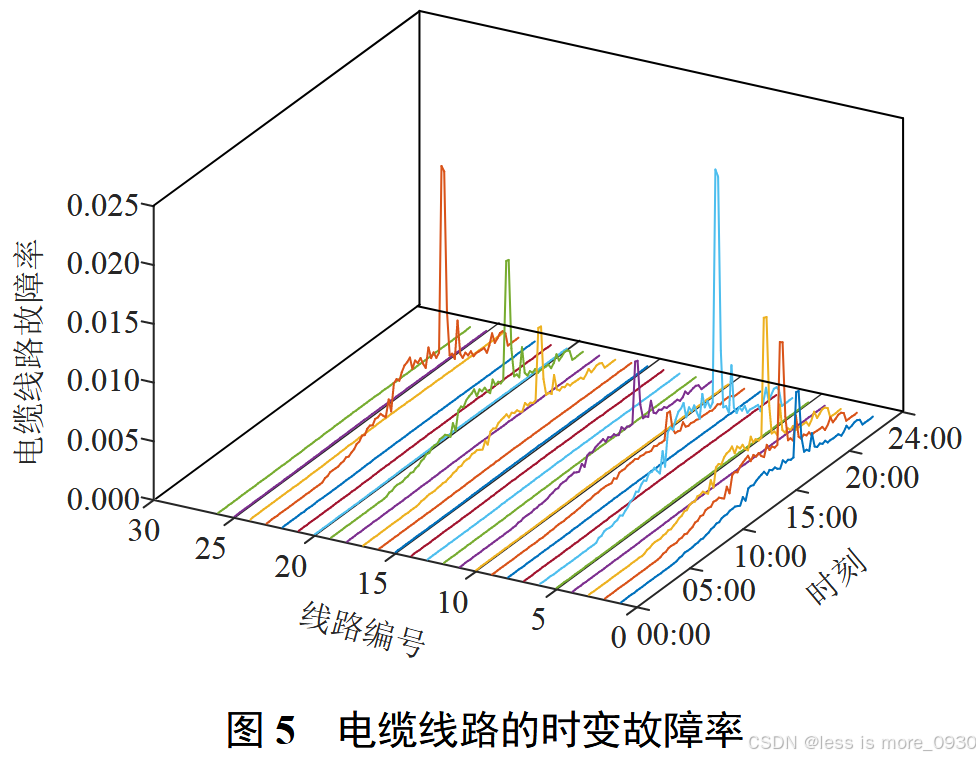
电缆接头热应力张量附图C4,由式(6)得到电缆接头时变故障率如图6。所受热应力张量较大的电缆接头与电缆缆芯温度较高的线路相符。由此说明电缆缆芯温度对电缆绝缘的热膨胀作用会加剧电缆接头故障的可能性。
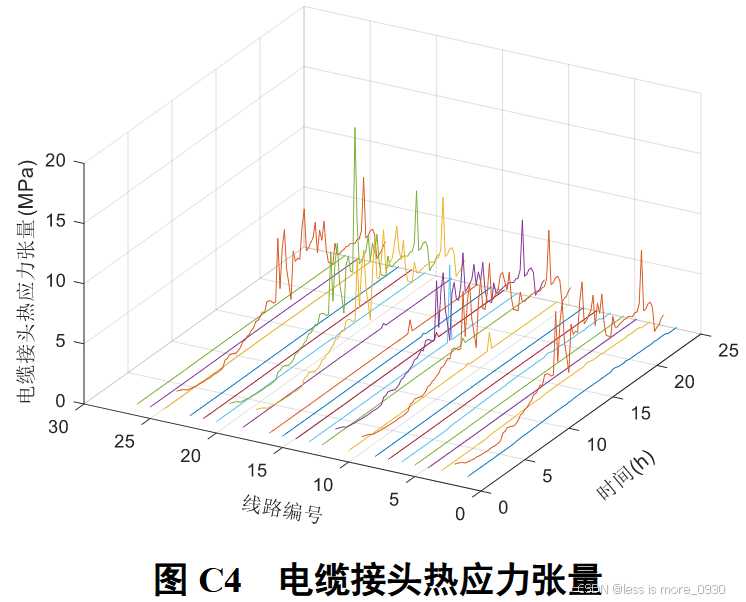
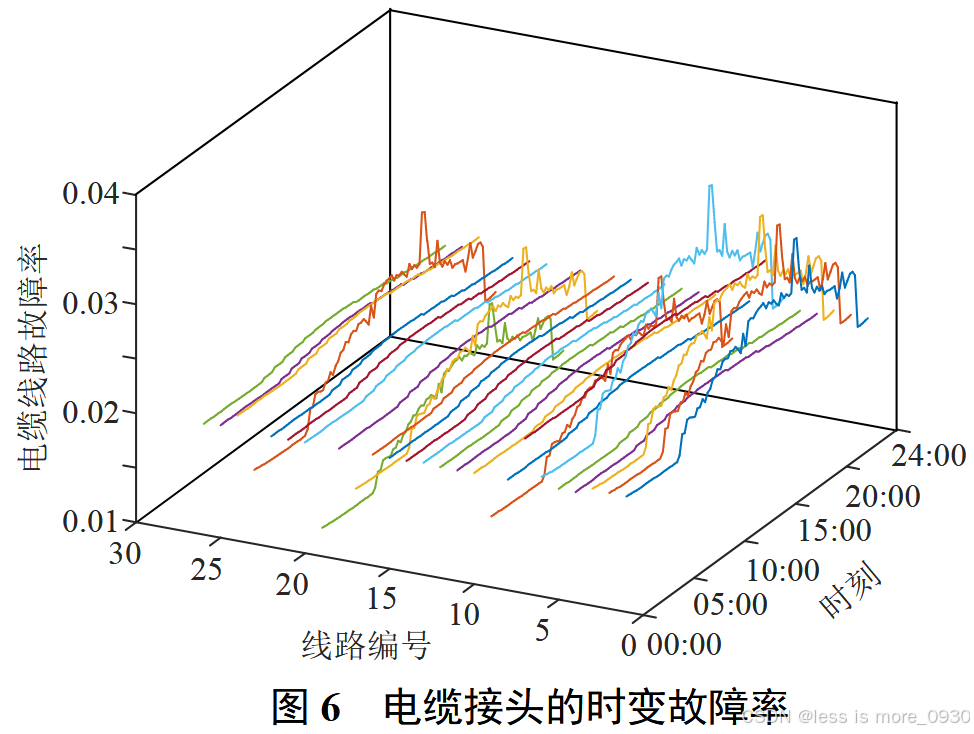
此外,对比图5和6可知,电缆型配电网中对应线路在极端高温时刻下接头故障率一般为其线路故障率的2~3倍,此结论也与实际电缆故障中电缆接头与电缆线故障比重相符。
利用式(7)得到的整条电缆未来 24 h 的故障率如图 7 所示。
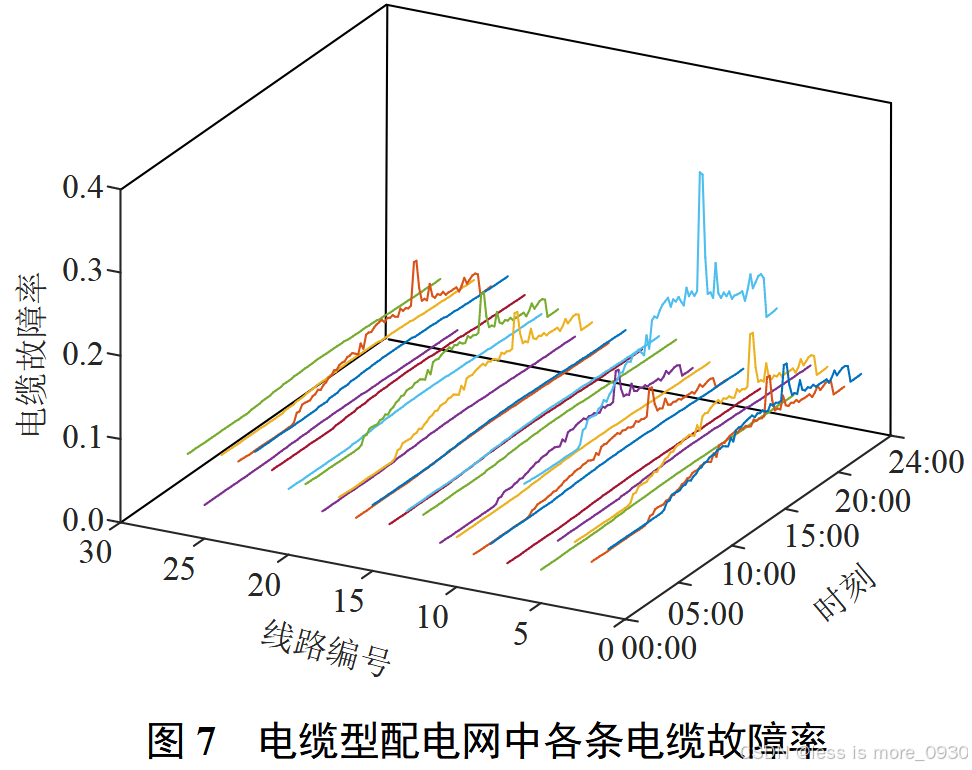
图7中电缆线路故障率峰值时段出现在极端高温时段,网络中主要电能传输线路1、2、3、6、9、11、17、19、23故障率明显高于其他电缆,电缆线路6在15:00达到全网最高故障率36.74%。
结合电缆故障率并进行 100 000 次蒙特卡洛抽样可得,发生故障的电缆条数概率分布如附图C5(a)所示。每次蒙特卡洛抽样的故障场景信息熵值形成的概率分布如附图C5(b)所示。
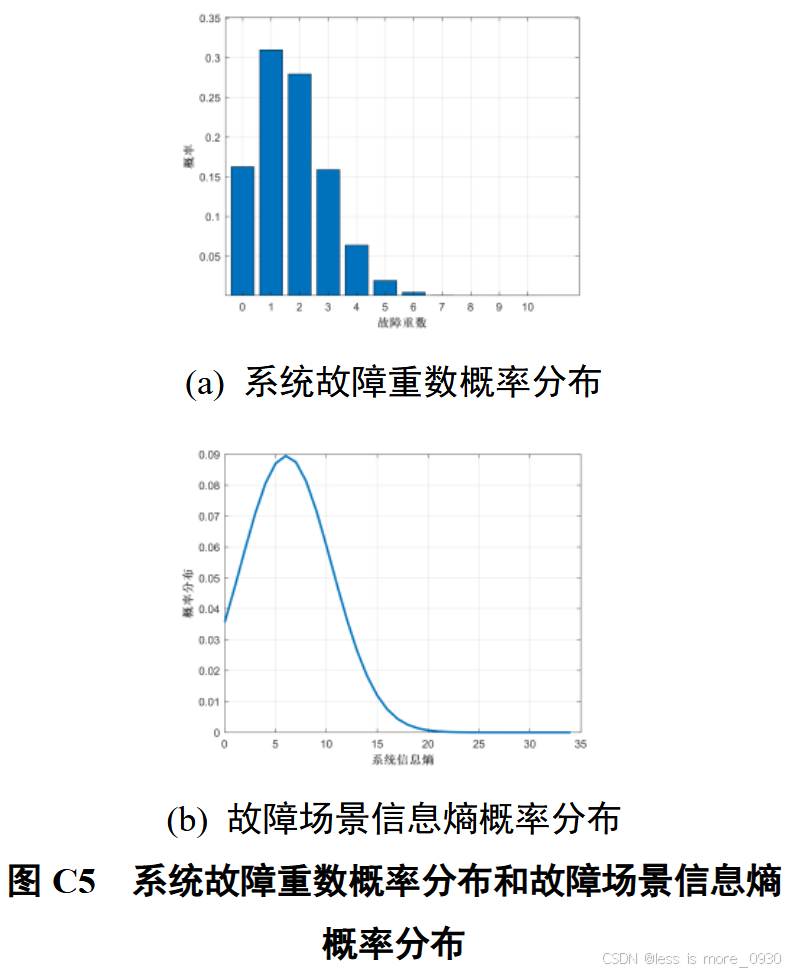
由附图C5(a)可知,电缆故障重数90%以上集中在0~3重,其中1~2重占比接近60%。附图C5(b)中95%场景的信息熵分布于(4.63,7.47)。
结合图7和附图C5,可设定极端高温灾害下电缆3、6在15:00发生故障,且电缆19、23因其运行温度高于130℃而短暂停运。其中,电缆3、6同时发生故障对应信息熵为5.14,属于附图C5(b)中的典型场景;被暂时停运的电缆19、23,需要派遣抢修小队对其降温。发生群发性故障后的电缆型配电网如附图C6所示。
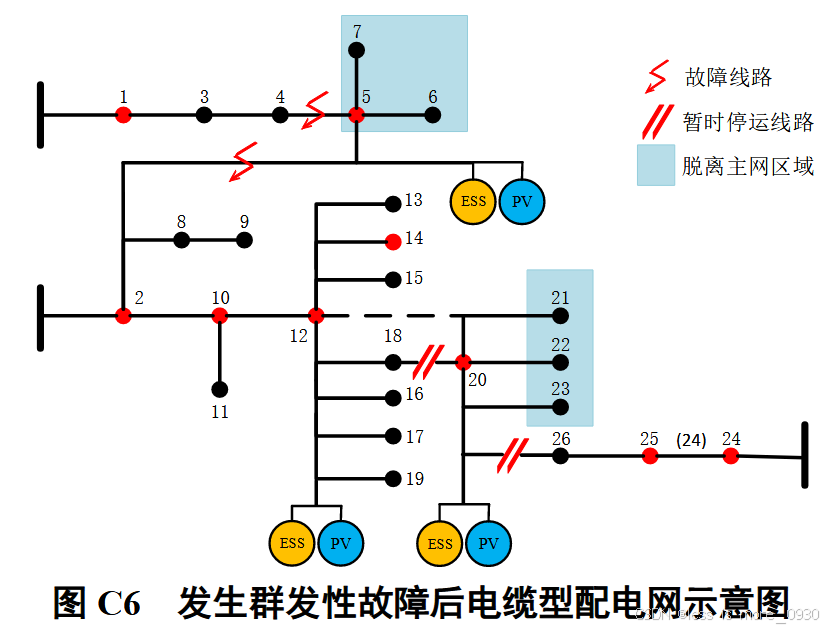
5.3 极端高温下电缆型配电网韧性提升策略分析
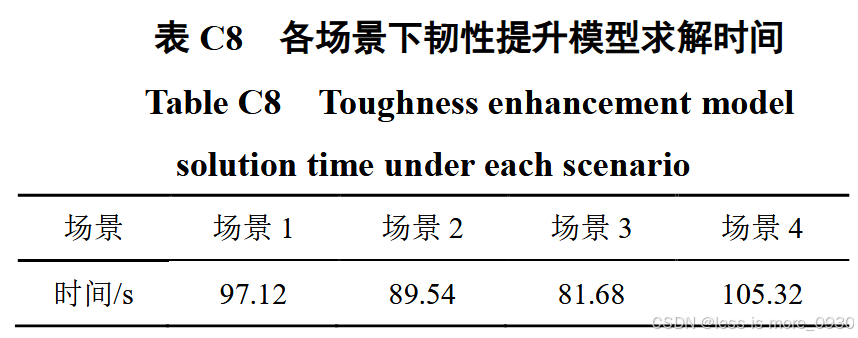
求解场景1、2、3、4中的韧性提升模型,求解时间参见附表C8。各场景网络重构与抢修流程如图8所示,各场景移动式应急发电车供电时刻见表2。

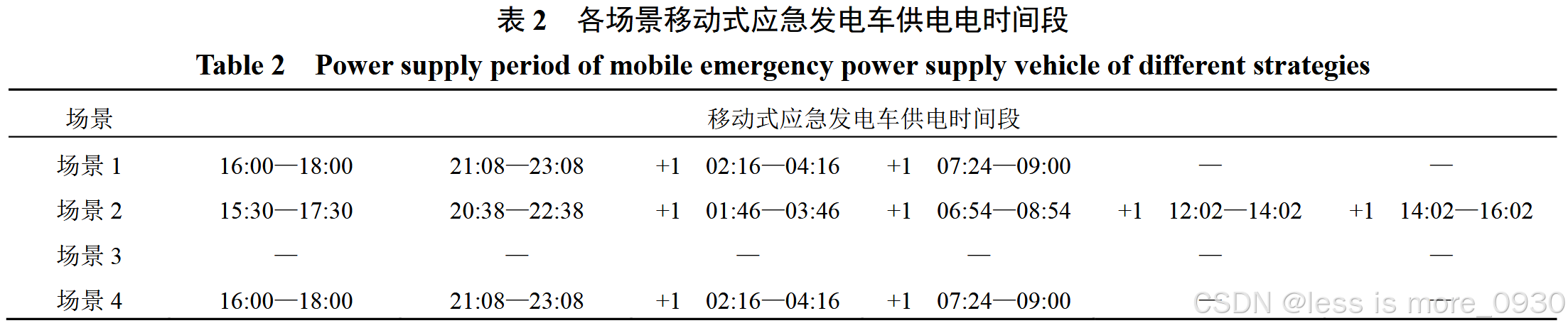
由图8与表2得到所提统筹考虑极端高温下电缆降温措施与配电网抢修供电措施的恢复流程为:
1)15:00故障发生时:通过闭合联络线26对节点21、22、23供电。节点5的DG离网运行为孤岛节点5、6、7供电。节点12、20的DG进入恢复运行状态,分担节点2的供电压力,降低电缆线路载流量从而降低电缆温度。同时抢修小队前往线路3、6进行抢修。
2)由于光伏出力在16:00后大幅下降导致光储系统难以维持整个孤岛所需用电量,因此15:30派遣应急发电车前往节点5为孤岛供电。
3)16:00---次日09:00间应急发电车与光储发电系统共同为节点5、6、7供电,期间在应急发电车与光储发电系统未同时充电时,节点5、6、7部分处于失电状态。
4)次日09:00---次日17:00光储发电系统可支撑节点5、6、7全部用电量,此时段不需要调用移动式应急发电车。
5)次日17:30线路3、6抢修完毕并重新投入运行,两支抢修小队分别前往故障线路19、23。
6)次日18:30线路19、23抢修完成同时,断开联络线26。
不同场景电缆网络损耗与关键负荷恢复量对比结果分别如图 9、10 所示。
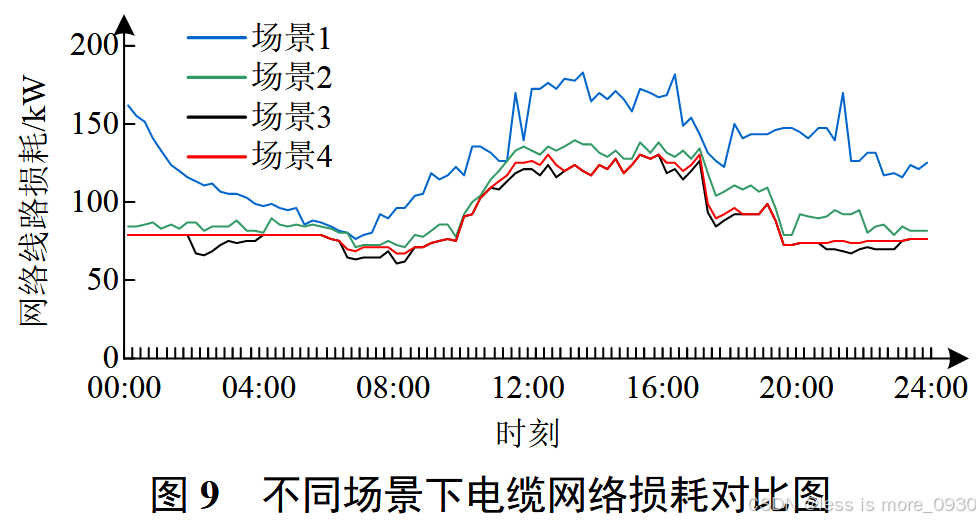
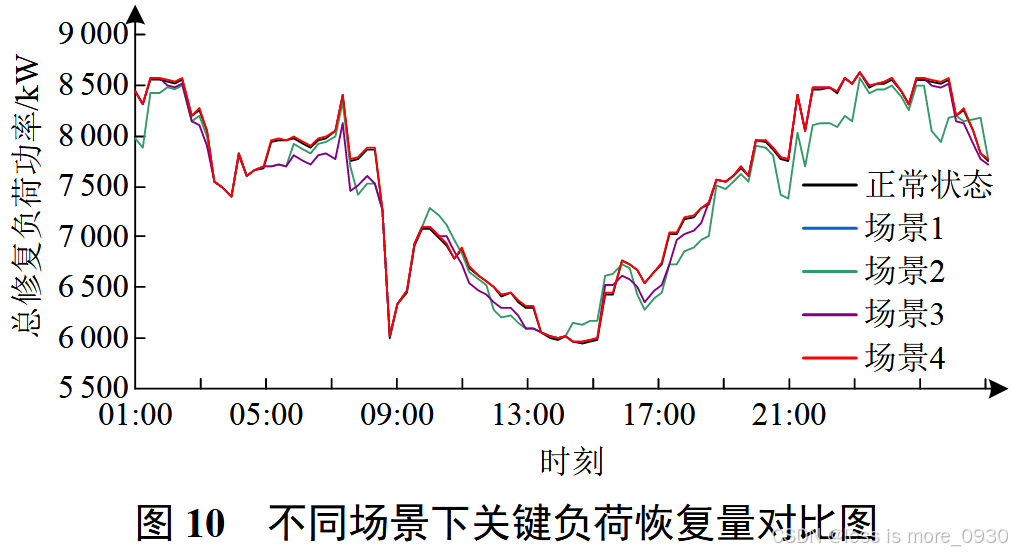
结合表2、图8---10,分别立足于高温电缆处理措施和电缆运行温度控制、DG孤岛、移动式应急发电车3个措施,对各场景的韧性提升策略进行对比分析:
(1)高温电缆处理与温度控制:能够改善潮流分布、降低线路电流和网络损耗,从而预防故障并提升电网防御力。
(2)分布式电源(DG)并网与孤岛运行:可分担供电压力、降低线路损耗,并为网络重构无法恢复的负荷提供紧急供电,增强协同恢复能力。
(3)移动式应急发电车:具备灵活供电特性,能补充网络重构与孤岛运行无法覆盖的供电缺口,最大范围保障电力供应。
6 结论
本文旨在提升极端高温灾害下电缆型配电网的韧性,通过综合考虑防御力、恢复力和协同力,提出了一套韧性提升策略。主要结论如下:
(1)建立了极端高温下电缆故障模型:量化分析了高温导致的绝缘老化和受热膨胀问题,为模拟和筛选电缆群发性故障场景提供了理论依据。
(2)构建了多维度的韧性量化指标体系:从防御力、恢复力、协同力三个维度,提出了包含网络损耗、线路抗灾贡献度、关键负荷恢复量等在内的量化指标,用于科学评估配电网的韧性水平。
(3)提出了协同优化的韧性提升模型:将短时停运降温措施与抢修供电措施进行协同优化,建立了考虑温度约束的韧性提升模型。验证结果表明,该模型能有效实现快速、最大范围恢复供电的目标。
该研究有助于提升电力系统应对极端高温灾害的能力,并为未来构建城市电力系统与应急管理部门之间的信息共享与联动机制提供了支持。
参考文献
1\]田书欣,肖文渊,符杨,等.极端高温灾害下电缆型配电网韧性提升策略研究\[J\].中国电机工程学报,2025,45(09):3408-3420.DOI:10.13334/j.0258-8013.pcsee.232406.