一.概述
根据之前写过的一篇文章:【算法】不懂数学原理也能看得懂的KMP算法,我们大致知道KMP算法的运行原理,在整个KMP算法中,最核心关键的部分就是next数组的搭建,关于next数组的代码实现,网上大多统一一个写法:
cpp
vector<int> buildNext(const string& pattern) {
int m = pattern.length();
vector<int> next(m, 0);
int j = 0;
for (int i = 1; i < m; ++i) {
while (j > 0 && pattern[i] != pattern[j]) {
j = next[j - 1];
}
if (pattern[i] == pattern[j]) {
++j;
}
next[i] = j;
}
return next;
}代码不过寥寥数语,就能将整个next数组的功能完完整整的实现出来,这让很多程序员都惊叹不已,想不明白这个代码究竟是怎么被设计出来的,其实代码只是将KMP算法推算出来的公式写成了代码而已,所以只要你理解了KMP算法的数学理论并且明白其推导过程,你就知道代码为什么会这么写了。
下面将尽可能用通俗易懂的词语来描述KMP的推导过程。总的来说,next数组的数学原理一共就两条:
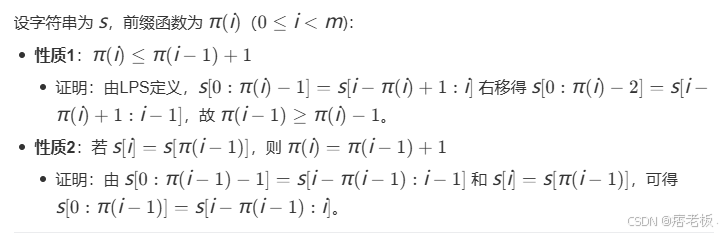
二.前缀函数
先来说明前缀函数:前缀函数 π(i) 表示字符串 s 的前 i+1 个字符组成的子串 s[0:i] 的最长公共真前缀后缀长度(LPS)。根据之前写过的文章:【算法】不懂数学原理也能看得懂的KMP算法中举过的例子,其字符串:
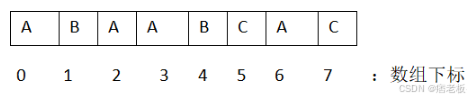
它每个排列组合的最长公共前后缀的长度分别是:
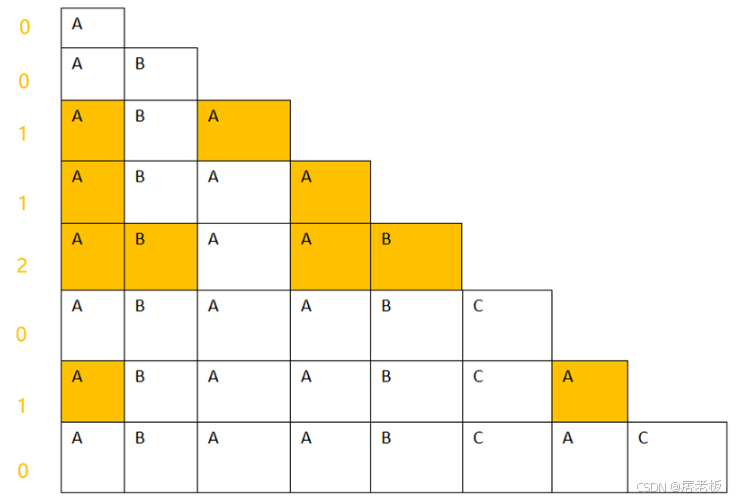
也就是说字符串"ABAABCAC"的前缀函数分别是:,
,
,
,
,
,
,
三.性质一:π(i)≤π(i−1)+1
该性质的含义:字串[0:i]的前缀函数π(i)长度不可能比它上一个前缀函数π(i)+1更大。
推导过程:假设我们已经知道 π(i) 的值(即子串 s[0:i] 的最长公共前后缀长度为 π(i))。根据 π(i) 的定义,我们可以写出π(i) 的LSP等式:
稍微提一嘴,同时我们也能写出π(i-1) 的LSP等式:
举个例子π(i) 的LSP等式 :假设我们有一个字符串 s = "ababaca",我们想要计算 π(5),最长公共前后缀是 "aba",长度为 3,所以π(5) = 3,所以左边 s[0:π(5)-1] 是 s[0:2],即 "ab",右边 s[5-π(5)+1:5] 是 s[3:5],即 "ab"
知道π(i)的定义,我们就可以根据它的定义反推得出它的上一个前缀函数 π(i-1) 的定义,将上述等式的两个区间同时向右移动一位(即去掉最后一个字符),因为原等式表示两个长度为 π(i) 的子串相等,所以去掉它们各自的最后一个字符后,剩下的长度为π(i-1) 的子串仍然相等,所以我们可以通过π(i)的等式来反推出π(i-1)的LSP等式:
以上公式的推导过程为:
由 π(i) 定义:s[0:π(i)-1] = s[i-π(i)+1:i]
两边同时去掉最后一个字符:
左侧:s[0:π(i)-1] 去掉最后一个字符 → s[0:π(i)-2]
右侧:s[i-π(i)+1:i] 去掉最后一个字符 → s[i-π(i)+1:i-1]
因此得到:s[0:π(i)-2] = s[i-π(i)+1:i-1]
观察以上两个公式,我们可以得出一个结论:移除一个字符后,原有最长前后缀的'缩短版'仍被包含在更短子串的公共前后缀中。
再举个例子解释一下上面过于抽象的概念: 以字符串 **s = "ABABA"** 为例,手工计算其前缀函数 π(i):
| i | s[0:i](前缀) | π(i)(最长公共真前后缀长度) | 备注 |
|---|---|---|---|
| 0 | A | 0 | 单个字符,无真前后缀 |
| 1 | AB | 0 | "AB" 的前后缀无相等(A ≠ B) |
| 2 | ABA | 1 | 前后缀 "A" = "A" |
| 3 | ABAB | 2 | 前后缀 "AB" = "AB" |
| 4 | ABABA | 3 | 前后缀 "ABA" = "ABA" |
我们观察 从i=4 反推 i=3 的情况,π(4) = 3,最长公共前后缀是 "ABA",当我们移除最后一个字符 s('A'),就变成了 π(3)=2,其最长公共前后缀是 "AB",我们会发现:"ABA" 移除最后一个字符 'A' 后,得到 "AB",它正是 π(3)=2 对应的最长公共前后缀。或者说,"AB" 的长度 2 正好是 "ABA" 长度 3 减去 1。
该性质揭示了 KMP 算法高效计算的关键:传递性,此性质作用如下:
(1)为了计算下一个前缀函数的π(i),我们不需从头开始匹配,而是基于当前的前缀函数π(i-1) 对应的匹配结果往前检查一个字符即可。
(2)该性质保证了 π(i) 不可能比 π(i-1) + 1 更大,确保了当新字符不匹配时,我们可以安全地回退到 π(i-1) 对应的公共前后缀长度继续检查,而不会漏掉可能的匹配。
如果用公式表示的话就是:
移项即得:
推导出来这个公式有什么用呢?在性质二里面就会用上。
四.性质二:s[i]==s[π(i−1)]?
该性质是整个next数组的匹配核心机制:**我们在知道π(i-1)的情况下,如何预测到π(i)是多少呢?**就是通过这个性质来进行预测的。我们继续用上面的例子来说明:
以字符串 **s = "ABABA"** 为例,手工计算其前缀函数 π(i):
| i | s[0:i](前缀) | π(i)(最长公共真前后缀长度) | 备注 |
|---|---|---|---|
| 0 | A | 0 | 单个字符,无真前后缀 |
| 1 | AB | 0 | "AB" 的前后缀无相等(A ≠ B) |
| 2 | ABA | 1 | 前后缀 "A" = "A" |
| 3 | ABAB | 2 | 前后缀 "AB" = "AB" |
| 4 | ABABA | 3 | 前后缀 "ABA" = "ABA" |
当我们的程序计算到i=3,也就是π(3)=2时,我们如何通过π(3)来预测π(4)是多少呢?首先,通过观察我们可以得知两个特点:
- i 表示的是后缀的最后一位字符的下标。
- π(i)表示的是前缀最后一位字符的下标 +1。
所以在π(3)=2时,i和π(3)所指向的位置如下图所示:
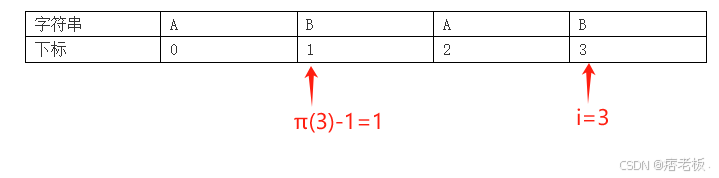
此时,我们需要计算i=4时,π(4)应该是多少,也就是说要对比前缀的最后一位和后缀的最后一位是否相等,根据上述特点,i 表示的是后缀的最后一位字符的下标,所以很自然的就能画出指针指向:

但是π(4)的指针指向多少呢?不好意思,我们不知道π(4)是多少,所以无法指向,但是我们知道s[4]的字符肯定是要和s[2]的字符进行对比的,而刚好π(3)=2:
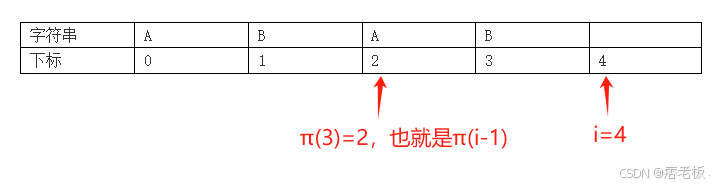
所以我们就得出了新一轮的判断对比公式是:
此处又能分出两个情况:
- 情况一:这俩位置的字符刚好相等,那就能直接得出π(i)是多少
- 情况二:如果这俩位置的字符不相等,那就需要启动回退匹配机制。
五.情况一:如果 s[i]=s[π(i−1)],那么 π(i)=π(i−1)+1
先来说明俩位置字符刚好相等时,如何求π(i)。
由上述可知**π(i-1)**的LSP公式为:
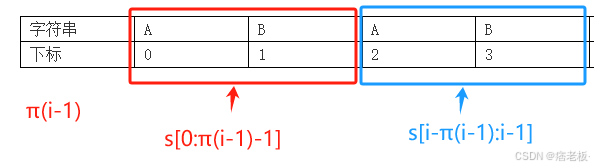
如果:
结合上述俩公式可得出π(i)新公式 :
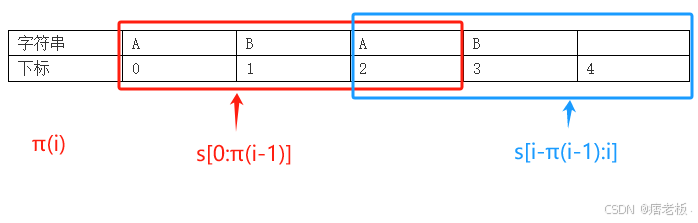
这个就是知道π(i-1)的情况下,如何预测到π(i)是多少。
依据 π(i) 定义得:,
结合性质一中通过π(i−1)推算出的性质:
结合上述两个定义可得:
六.情况二:如果 s[i]!=s[π(i−1)],则启动回退匹配机制
这种情况比较简单,直接上伪代码就能看懂了:
cpp
令π(i-1)=j
if(s[j]==s[i])
{
π(i) =π(i-1)+1;
}
else
{
j`=π(j-1);
#继续回到s[j]==s[i]判断中
}
#如此循环,直到j==0 || s[j]==s[i]为止如此,next数组的数学推导就已经全部解释完成,我们只要将上述两个性质写成代码,就是开头那段next数组代码的构建原理。