目录
[1. 向量化操作:告别冗余循环](#1. 向量化操作:告别冗余循环)
[2. 内存管理与数据类型优化](#2. 内存管理与数据类型优化)
[3. 使用内置工具箱加速复杂算法](#3. 使用内置工具箱加速复杂算法)
[4. JIT 编译加速 (Just-In-Time Compilation)](#4. JIT 编译加速 (Just-In-Time Compilation))

如果您喜欢此文章,请收藏、点赞、评论,谢谢,祝您快乐每一天。
MATLAB(Matrix Laboratory)作为工程计算和数值分析领域的强大工具,其内置的向量化操作、丰富的工具箱以及优化的底层编译机制,使其在处理大规模数据分析和复杂算法优化时具有天然的优势。
以下将分享几个 MATLAB 在数据分析与算法优化中的高效应用案例。
1. 向量化操作:告别冗余循环
MATLAB 的核心效率来源于其对矩阵和向量操作的原生支持。与 C/C++ 或传统解释型语言不同,MATLAB 的许多内置函数都是高度优化的底层代码(通常是 C 或 Fortran 编写),执行向量化操作可以避免低效的 for 循环。
案例:大规模数据滤波
假设我们需要对一个包含百万级数据点的向量 X 进行一个简单的线性变换 Yi=aXi+b。如图:
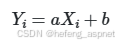
低效(循环)实现:
N = 1000000;
X = rand(N, 1); % 随机生成百万数据点
a = 2;
b = 5;
Y_loop = zeros(N, 1);
tic; % 开始计时
for i = 1:N
Y_loop(i) = a * X(i) + b;
end
time_loop = toc;
disp(['循环耗时: ', num2str(time_loop)]);
高效(向量化)实现:
tic; % 开始计时
Y_vector = a * X + b; % 直接对整个向量进行运算
time_vector = toc;
disp(['向量化耗时: ', num2str(time_vector)]);
效率提升: 在实际运行中,向量化操作的速度通常比循环快 10倍到数百倍,具体取决于操作的复杂度和数据规模。

2. 内存管理与数据类型优化
处理大数据集时,选择合适的数据类型至关重要,这直接影响内存占用和计算速度(尤其是在内存访问受限的场景下)。
案例:存储优化
假设需要存储一个 1000x1000 的矩阵,元素值范围在 0 到 100 之间。
低效实现(默认双精度):
MATLAB 默认使用 double (64位浮点数),占用 1000×1000×8 字节 ≈8 MB。
高效实现(单精度/整数):
如果数据是整数且范围较小,应使用更紧凑的类型。
% 场景一:数据范围在 0 到 255 之间 (使用 uint8)
Data_uint8 = uint8(randi([0, 255], 1000, 1000));
% 占用: 1000 * 1000 * 1 字节 = 1 MB
% 场景二:数据为浮点数但精度要求不高 (使用 single)
Data_single = single(rand(1000, 1000));
% 占用: 1000 * 1000 * 4 字节 = 4 MB
效率提升: 减少了内存占用,使得更大的数据集可以放入缓存中,从而减少了I/O操作,间接提高了运算速度。
3. 使用内置工具箱加速复杂算法
MATLAB 的强大之处在于其高度专业的工具箱,这些工具箱的函数经过了严格的性能优化,通常比自己从头编写的 M 语言代码快得多。
案例:大规模矩阵求逆与线性系统求解
在许多优化算法(如最小二乘法、迭代算法)中,需要频繁求解大型线性方程组 Ax=b。如图:
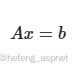
低效实现(尝试迭代求解或使用通用函数):
% 假设 A 是一个 5000x5000 的稀疏矩阵
A = sprand(5000, 5000, 0.01);
b = rand(5000, 1);
% 较慢的迭代求解或通用求逆
X_slow = A \ b; % 可能会退化成通用求解器
高效实现(利用稀疏矩阵优化器):
当矩阵 A 是稀疏的时,应使用专门的稀疏矩阵求解器,如 mldivide 遇到稀疏矩阵时会自动触发高度优化的稀疏算法。
% 确保 A 被识别为稀疏矩阵(如果 A 已经生成为稀疏结构,则无需此步)
A_sparse = sparse(A);
tic;
X_fast = A_sparse \ b; % 自动调用高度优化的稀疏线性求解器 (e.g., UMFPACK)
time_sparse = toc;
效率提升: 对于稀疏矩阵,专用稀疏求解器的速度比通用稠密求解器快数个数量级,因为它们只处理非零元素。
4. JIT 编译加速 (Just-In-Time Compilation)
对于那些无法完全向量化的算法(例如复杂的状态机、需要大量条件判断的自定义迭代),MATLAB 的 JIT 编译器可以显著加速 M 文件的执行。
- 使用
fcn2struct或compile(2018b 之后): 通过将 M 函数编译成 MEX 函数或 JIT 编译对象,MATLAB 可以将 M 代码转化为机器码,从而接近 C/C++ 的执行速度。
应用场景: 在自定义的粒子群优化 (PSO) 或遗传算法的适应度函数中,如果内部逻辑复杂,JIT 编译能带来显著加速。
总结
在 MATLAB 中实现高效算法的关键在于:
- 优先向量化: 总是尝试用矩阵和向量运算替代循环。
- 精选数据类型: 根据数据的实际范围和性质,选择最节省内存的类型(如
uint8,single)。 - 善用工具箱: 相信内置的优化函数(如稀疏求解器、FFT、信号处理函数)的性能。
- 必要时 JIT 编译: 对复杂的非向量化函数,利用 JIT 编译器进一步提速。
如果您喜欢此文章,请收藏、点赞、评论,谢谢,祝您快乐每一天。