数据结构第三章：栈、队列与数组

一、知识框架总览

线性表
├── 操作受限
│   ├── 栈
│   │   ├── 顺序栈
│   │   ├── 链栈
│   │   └── 共享栈
│   └── 队列
│       ├── 循环队列
│       ├── 链式队列
│       └── 双端队列
└── 推广
    └── 数组
        ├── 一维数组
        └── 多维数组：压缩存储、稀疏矩阵

二、栈（Stack）------ 操作受限的线性表

✅ 定义

栈是一种只允许在一端进行插入和删除操作 的线性表，遵循 LIFO（Last In First Out） 原则。

• 栈顶（Top）：允许插入/删除的一端
• 栈底（Bottom）：固定不变的一端
• 空栈：栈中无元素

✅ 基本操作（通用接口）

操作	功能
InitStack(&S)	初始化空栈
DestroyStack(&S)	销毁栈
StackEmpty(S)	判断是否为空
StackLength(S)	返回栈长度
Push(&S, e)	入栈（在栈顶插入元素 e）
Pop(&S, &e)	出栈（删除栈顶元素，并返回其值）
GetTop(S, &e)	获取栈顶元素（不删除）

---

1. 顺序栈（Sequential Stack）

🔹 结构定义

#define MaxSize 50 //定义栈中元素的最大个数
typedef struct {
    ElemType data[MaxSize]; //存放栈中元素
    int top; //栈顶指针
} SqStack;

🔹 操作实现

（1）初始化

#define MaxSize 50 //定义栈中元素的最大个数
typedef struct {
    ElemType data[MaxSize]; //存放栈中元素
    int top; //栈顶指针
} SqStack;

// 初始化 
void InitStack(SqStack &S) {
    S.top = -1; // 初始化指针
} 

（2）判栈空

#define MaxSize 50 //定义栈中元素的最大个数
typedef struct {
    ElemType data[MaxSize]; //存放栈中元素
    int top; //栈顶指针
} SqStack;

// 判栈空
bool StackEmpty(SqStack S) {
    if(S.top == -1) { //栈空
        return true;
    } else {
        return false;
    }
}

（3）入栈

#define MaxSize 50 //定义栈中元素的最大个数
typedef struct {
    ElemType data[MaxSize]; //存放栈中元素
    int top; //栈顶指针
} SqStack;

// 入栈
bool Push(SqStack &S, ElemType x) {
    if(S.top == MaxSize - 1) { // 栈满，报错
        return false;
    }
    S.data[++S.top] = x; //指针先加1,再入栈
    return true;
}

（4）出栈

// 出栈
bool Pop(SqStack &S, ElemType &x) {
    if(S.top == -1) { // 空栈，报错
        return false;
    }
    x = S.data[S.top--]; // 先出栈，指针再减1
    return true;
}

（5）获取栈顶元素

#define MaxSize 50 //定义栈中元素的最大个数
typedef struct {
    ElemType data[MaxSize]; //存放栈中元素
    int top; //栈顶指针
} SqStack;

// 读栈顶元素
bool GetTop(SqStack S, ElemType &x) {
    if(S.top == -1) {
        return false;
    }
    x = S.data[S.top];
    return true;
}

🔹 特点

• ✅ 支持随机访问（但通常不使用）
• ❌ 栈满时需扩容或报错
• 📌 栈顶指针 top 从 -1 开始

---

2. 链栈（Linked Stack）

🔹 结构定义

// 栈的链式存储结构
typedef struct LinkNode {
    ElemType data; //数据域
    struct LinkNode *next; //指针域
} LinkStack; // 栈类型定义

⚠️ 注意：链栈通常不带头节点，头指针指向栈顶。

🔹 操作实现

（1）初始化

// 栈的链式存储结构
typedef struct LinkNode {
    ElemType data; //数据域
    struct LinkNode *next; //指针域
} LinkNode, *LinkStack; // 栈类型定义

// 链栈初始化
void InitLinkStack(LinkStack &S) {
    S = NULL;
}

（2）入栈

// 栈的链式存储结构
typedef struct LinkNode {
    ElemType data; //数据域
    struct LinkNode *next; //指针域
} LinkNode, *LinkStack; // 栈类型定义

// 链栈入栈操作（头插法）
bool Push(LinkStack &S, ElemType x) {
    // 新建结点
    LinkNode *p = new LinkNode();
    // 设置入栈结点的数据值
    p -> data = x;
    // 插入结点
    p -> next = S -> next;
    S -> next = p;
    return true;
}

（3）出栈

// 栈的链式存储结构
typedef struct LinkNode {
    ElemType data; //数据域
    struct LinkNode *next; //指针域
} LinkNode, *LinkStack; // 栈类型定义

// 链栈出栈操作
bool Pop(LinkStack &S, ElemType &x) {
    // 链栈为空，报错
    if(S -> next == NULL) {
        return false;
    }
    // 获取待删除的结点
    LinkNode *q = S -> next;
    // 返回删除结点的数据值
    x = q -> data;
    // S -> next 指向S的后面第二个结点
    S -> next = q -> next;
    // 释放删除的结点
    free(q);
    return true;
}

（4）获取栈顶

// 栈的链式存储结构
typedef struct LinkNode {
    ElemType data; //数据域
    struct LinkNode *next; //指针域
} LinkNode, *LinkStack; // 栈类型定义

// 链栈获取栈顶元素
bool GetTop(LinkStack &S, ElemType &x) {
    // 空栈，报错
    if(S -> next == NULL) {
        return false;
    }
    // 获取栈顶结点
    LinkNode *p = S -> next;
    x = p -> data;
    return true;
}

🔹 特点

• ✅ 动态分配，不会溢出
• ✅ 插入/删除 O(1)
• ❌ 不支持随机访问

---

3. 共享栈（Shared Stack）

🔹 设计思想

两个栈共享同一段连续内存空间，一个从左向右增长，另一个从右向左增长，提高空间利用率。

🔹 结构定义

#define MAXSIZE 100
typedef struct {
    ElemType data[MAXSIZE];
    int top1; // 第一个栈的栈顶
    int top2; // 第二个栈的栈顶
} SharedStack; 

🔹 初始化

#define MAXSIZE 100
typedef struct {
    ElemType data[MAXSIZE];
    int top1; // 第一个栈的栈顶
    int top2; // 第二个栈的栈顶
} SharedStack;

// 共享栈初始化
void InitSharedStack(SharedStack &S) {
    S.top1 = -1;
    S.top2 = MaxSize;
}

🔹 入栈（以栈1为例）

#define MAXSIZE 100
typedef struct {
    ElemType data[MAXSIZE];
    int top1; // 第一个栈的栈顶
    int top2; // 第二个栈的栈顶
} SharedStack;

// 共享栈入栈
bool Push1(SharedStack &S, ElemType x) {
    if(S.top1 + 1 == S.top2) { // 栈满，报错
        return false;
    }
    S.data[++S.top1] = x;
    return true;
}

}

🔹 特点

• ✅ 提高空间利用率
• ❌ 两个栈大小动态变化，可能一方用不完另一方已满
• 📌 仅适用于两个栈最大长度之和 ≤ MAXSIZE 的场景

---

三、队列（Queue）------ 操作受限的线性表

✅ 定义

队列是一种只允许在一端插入、另一端删除 的线性表，遵循 FIFO（First In First Out） 原则。

• 队头（Front）：删除端
• 队尾（Rear）：插入端

✅ 基本操作（通用接口）

操作	功能
InitQueue(&Q)	初始化空队列
DestroyQueue(&Q)	销毁队列
QueueEmpty(Q)	判断是否为空
QueueLength(Q)	返回队列长度
EnQueue(&Q, e)	入队（在队尾插入）
DeQueue(&Q, &e)	出队（删除队头元素）
GetHead(Q, &e)	获取队头元素（不删除）

---

1. 循环队列（Circular Queue）

🔹 问题：假溢出

普通顺序队列中，rear == MAXSIZE - 1 时无法再入队，即使前面有空位。

🔹 解决方案：循环队列

将数组首尾相连，形成环状结构。

🔹 结构定义

#define MaxSize 50 //定义队列中元素的最大个数
typedef struct {
    ElemType data[MaxSize]; //用数组存放队列元素
    //队头指针和队尾指针
    int front;
    int rear;
} SqQueue;

🔹 关键技巧

• 判空条件 ：front == rear
• 判满条件 ：(rear + 1) % MAXSIZE == front（牺牲一个空间）
• 入队 ：rear = (rear + 1) % MAXSIZE
• 出队 ：front = (front + 1) % MAXSIZE

🔹 操作实现

（1）初始化

#define MaxSize 50 //定义队列中元素的最大个数
typedef struct {
    ElemType data[MaxSize]; //用数组存放队列元素
    //队头指针和队尾指针
    int front;
    int rear;
} SqQueue;

// 队列初始化
void InitQueue(SqQueue &Q) {
    Q.front = 0;
    Q.rear = 0;
}

（2）判空

#define MaxSize 50 //定义队列中元素的最大个数
typedef struct {
    ElemType data[MaxSize]; //用数组存放队列元素
    //队头指针和队尾指针
    int front;
    int rear;
} SqQueue;

// 判队空 
void QueueEmpty(SqQueue Q) {
    if(Q.front == Q.rear) { // 队空条件
        return true;
    } else {
        return false;
    }
} 

（3）入队

// 队列初始化
void InitQueue(SqQueue &Q) {
    Q.front = 0;
    Q.rear = 0;
}

// 入队
bool EnQueue(SqQueue &Q, ElemType x) {
    // 队满,报错
    if((Q.rear + 1) % MaxSize == Q.front) {
        return false;
    }
    // 入队
    Q.data[Q.rear] = x;
    Q.rear = (Q.rear + 1) % MaxSize; //队尾指针加1取模
    return true;
}

（4）出队

// 队列初始化
void InitQueue(SqQueue &Q) {
    Q.front = 0;
    Q.rear = 0;
}

// 出队
bool DeQueue(SqQueue &Q, ElemType &x) {
    // 队空，报错
    if(Q.rear == Q.front) {
        return false;
    }
    // 返回出队的值
    x = Q.data[Q.front];
    //队头指针加1取模
    Q.front = (Q.front + 1) % MaxSize;
    return true;
}

🔹 特点

• ✅ 避免假溢出
• ✅ 时间复杂度 O(1)
• ❌ 需牺牲一个空间判断满

---

2. 链式队列（Linked Queue）

🔹 结构定义

typedef struct LinkNode { // 链式队列起点
    ElemType data;
    struct LinkNode *next;
} LinkNode;

typedef struct { // 链式队列
    LinkNode *front, *rear; // 链式队列的起点和终点
} LinkQueue;

🔹 操作实现

（1）初始化

typedef struct LinkNode { // 链式队列起点
    ElemType data;
    struct LinkNode *next;
} LinkNode;

typedef struct { // 链式队列
    LinkNode *front, *rear; // 链式队列的起点和终点
} LinkQueue;

// 初始化链式队列
void InitQueue(LinkQueue &Q) {
    Q.front = Q.rear = new LinkNode(); // 建立头结点
    Q.front -> next = NULL; // 初始为空
}

（2）判队空

typedef struct LinkNode { // 链式队列起点
    ElemType data;
    struct LinkNode *next;
} LinkNode;

typedef struct { // 链式队列
    LinkNode *front, *rear; // 链式队列的起点和终点
} LinkQueue;

// 判队空
bool isEmpty(LinkQueue Q) {
    if(Q.front == Q.rear) { // 判空条件
        return true;
    } else {
        return false;
    }
}

（3）入队

typedef struct LinkNode { // 链式队列起点
    ElemType data;
    struct LinkNode *next;
} LinkNode;

typedef struct { // 链式队列
    LinkNode *front, *rear; // 链式队列的起点和终点
} LinkQueue;

// 链式队列入队
void enQueue(LinkQueue &Q, ElemType x) {
    // 创建待入队结点
    LinkNode *s = new LinkNode();
    // 设置入队结点的数据值
    s -> data = x;
    // 入队
    Q.rear -> next = s;
    // 入队结点设为尾结点
    Q.rear = s;
    // 尾结点指向刚入队的结点
    s -> next = NULL;
}

（4）出队

typedef struct LinkNode { // 链式队列起点
    ElemType data;
    struct LinkNode *next;
} LinkNode;

typedef struct { // 链式队列
    LinkNode *front, *rear; // 链式队列的起点和终点
} LinkQueue;

// 链式队列出队
bool DeQueue(LinkQueue &Q, ElemType &x) {
    // 队空，报错
    if(Q.rear == Q.front) {
        return false;
    }
    // 获取待出队的结点
    LinkNode *q = Q.front -> next;
    // 返回出队的值
    x = q -> data;
    // 出队
    Q.front -> next = q -> next;
    // 出队的结点是尾结点，删除后变空
    if(q == Q.rear) {
        Q.rear = Q.front;
    }
    // 释放出队结点
    free(q);
    return true;
}

🔹 特点

• ✅ 无需预分配空间
• ✅ 不会溢出
• ❌ 需维护两个指针（front 和 rear）

---

3. 双端队列（Deque）

🔹 定义

双端队列（Double-ended Queue）允许在两端进行插入和删除操作。

🔹 分类

• 输入受限双端队列：只能在一端插入，两端删除
• 输出受限双端队列：只能在一端删除，两端插入

🔹 应用

• 浏览器前进/后退
• 缓冲区管理

✅ 考研提示：双端队列多为选择题考查，重点理解概念。

---

四、数组（Array）------ 线性表的推广

✅ 定义

数组是由n 个相同类型元素组成的有序集合，元素通过下标直接访问。

✅ 一维数组

🔹 存储方式

连续内存单元，按行优先存储。

🔹 地址计算

地址 = base + i × sizeof(ElemType)

🔹 示例

int a[10]; // 一维数组

---

✅ 多维数组

🔹 二维数组（以行优先为例）

int a[3][4]; // 3 行 4 列

🔹 地址计算

a[i][j] 的地址 = base + (i × m + j) × sizeof(ElemType)

其中 m 是列数。

---

✅ 压缩存储与稀疏矩阵

🔹 压缩存储

1. 对称矩阵（存下三角，含对角线）

A = [ a₁₁
      a₂₁ a₂₂
      a₃₁ a₃₂ a₃₃
      ⋮   ⋮   ⋮   ⋱ ]

• 存储元素个数：

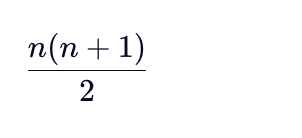
• 一维数组下标 k 的计算公式（矩阵行列号 i, j 从 1 开始；数组下标 k 从 0 开始）：

若 i >= j （下三角或对角线）：

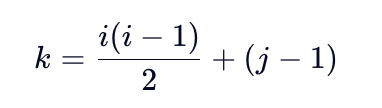
若 i ﹤ j （上三角）：

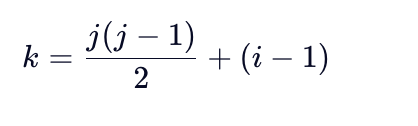
💡 原理：上三角元素 A[i][j] = A[j][i]，转为下三角位置计算。

---

2. 下三角矩阵（主对角线以下含对角线有效，上方为常数）

A = [ a₁₁
      a₂₁ a₂₂
      a₃₁ a₃₂ a₃₃
      ⋮   ⋮   ⋮   ⋱
      aₙ₁ ...       aₙₙ ]

存储元素数：

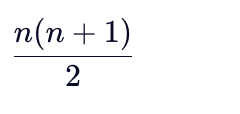
• 仅当 i ≥ j 时有定义，公式为：

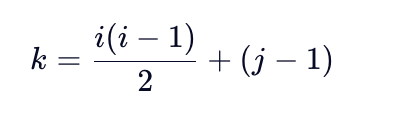
• 若 i < j ，值为常数（如 0），不存储。

🔸 公式与对称矩阵下三角完全相同。

---

3. 三对角矩阵（仅主对角线及其上下邻对角线非零）

A = [ a₁₁ a₁₂
      a₂₁ a₂₂ a₂₃
          a₃₂ a₃₃ a₃₄
              ⋱   ⋱   ⋱
                  aₙ₋₁,ₙ
                      aₙ,ₙ₋₁ aₙₙ ]

• 非零元素总数：

• 当 ∣i−j∣ ≤ 1 时（即元素在三条对角线上），其在一维数组中的下标为：

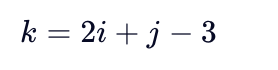
✅ 验证：

• A[1][1] \rightarrow k = 2×1 + 1 - 3 = 0
• A[2][3] \rightarrow k = 2×2 + 3 - 3 = 4

---

✅ 所有公式均基于：

• 矩阵行列号 i, j 从 1 开始
• 一维数组下标 k 从 0 开始

此即考研标准设定。

🔹 稀疏矩阵

• 定义：非零元素远少于总元素数的矩阵
• 存储方式：三元组表（行号、列号、值）

🔹 三元组结构

typedef struct {
    int row;     // 行号
    int col;     // 列号
    ElemType val; // 值
} Triple;

typedef struct {
    Triple data[MAXSIZE];
    int tu;      // 非零元素个数
    int mu, nu;  // 行数、列数
} SparseMatrix;

🔹 特点

• ✅ 节省空间
• ❌ 访问效率低（不能随机访问）
• 📌 考研常考：稀疏矩阵的三元组表示法

---

五、栈、队列、数组对比总结

特性	栈	队列	数组
操作限制	仅栈顶插入/删除	仅队尾入队、队头出队	任意位置可读写
逻辑结构	LIFO	FIFO	无限制
存储方式	顺序/链式	顺序/链式	顺序存储
时间复杂度	O(1)	O(1)	O(1)（随机访问）
典型应用	函数调用、括号匹配	打印机任务、缓冲区	数据批量处理

---

六、栈和队列的应用

栈的应用

🔹 括号匹配

利用栈检查表达式中圆括号、方括号等是否正确配对。遇到左括号入栈，遇到右括号则弹出栈顶并与之匹配。最终栈空且无失配，则合法。

🔹 表达式求值

1. 算数表达式

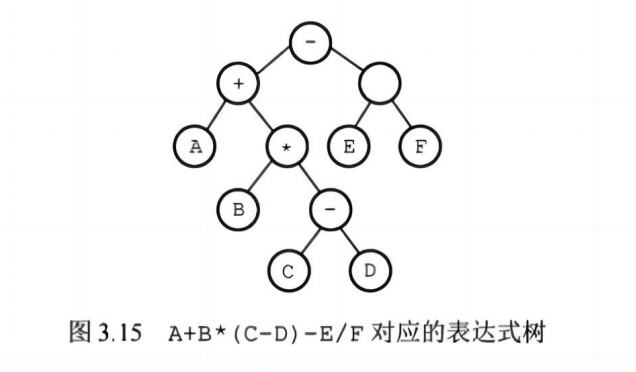
2. 中缀表达式转后缀表达式

规则：

1. 遇到字母或数字（操作数）→ 直接写下来
   👉 比如看到 A，马上写到结果里。
2. 遇到 ( → 直接压入栈
   👉 括号先存起来，等后面处理。
3. 遇到 ) → 把栈里的运算符一个个弹出来，写到结果里，直到碰到 ( 为止；然后把 ( 扔掉（不写）
   👉 括号包住的部分优先算完。
4. 遇到 + - * / 等运算符 →
   • 如果栈顶的运算符优先级 ≥ 当前这个，就先把栈顶的弹出来写到结果里；
   • 一直弹，直到栈顶优先级 < 当前，或者栈顶是 (；
   • 然后把当前运算符压入栈。

🔑 优先级：* 和 / 比 + 和 - 高

同级运算符（比如 + 和 -）按从左到右算，所以左边的先出栈

示例：

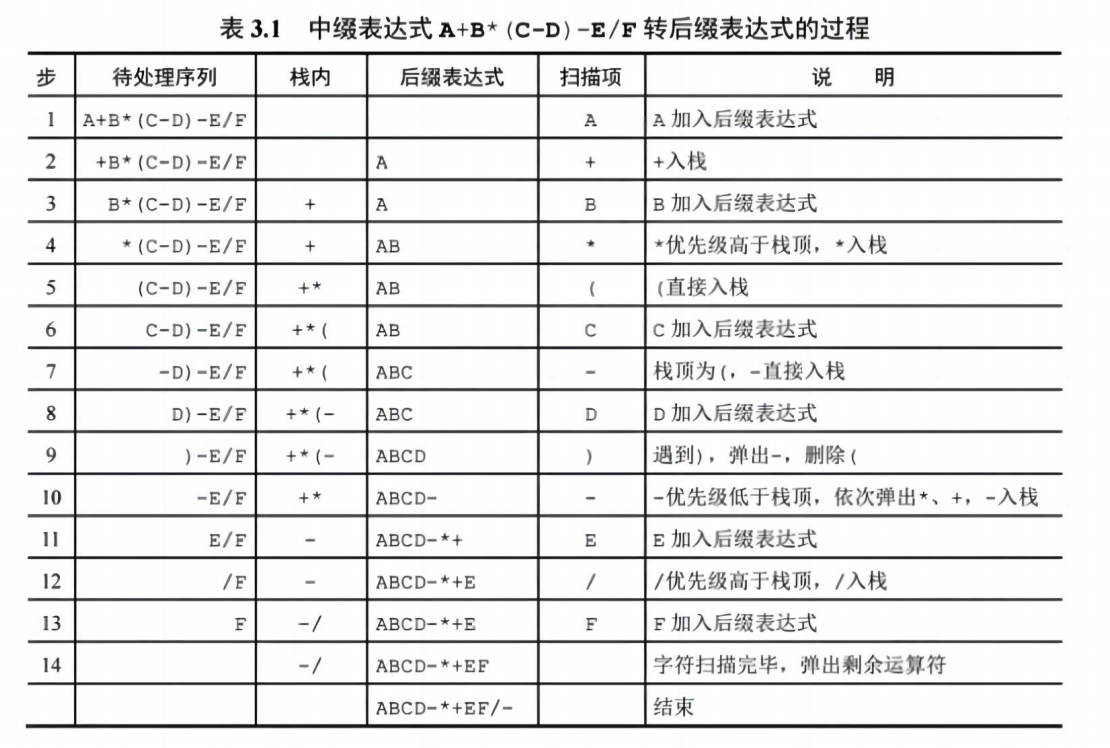
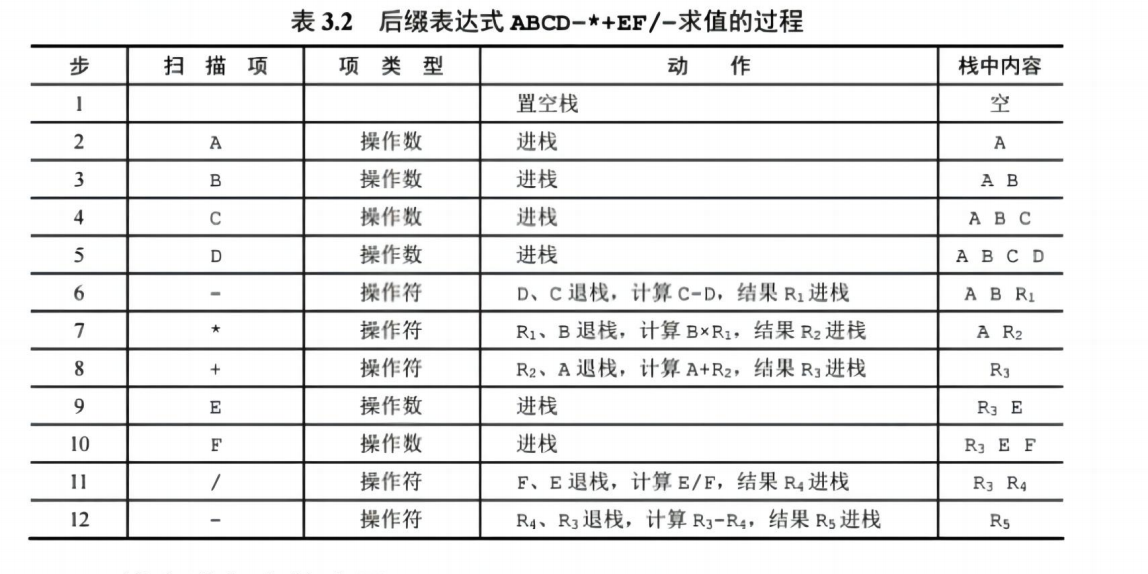
3. 后缀表达式求值

1. 从左到右扫描每一个元素。
2. 如果是数字 → 直接压入栈。
3. 如果是运算符（如 + - * /）→
   • 弹出栈顶两个数 （先弹出的是右操作数 ，后弹出的是左操作数）；
   • 计算：左 操作符 右；
   • 把结果压回栈中。
4. 最后栈里只剩一个数 → 就是最终结果！

⚠️ 注意顺序：

遇到 - 或 / 时，先弹出的是减数或除数 ！

例如：栈中有 [5, 2]（2 在顶），遇到 - → 算 5 - 2 = 3

---

示例：

🔹 递归

• 递归调用时，系统自动使用栈保存返回地址、参数和局部变量。
• 每次函数调用 → 入栈 ；每次函数返回 → 出栈。
• 递归必须有终止条件，否则栈会溢出（栈满）。
• 任何递归算法都可改写为非递归形式 ，需显式使用栈模拟调用过程。

示例：

int F(int n) { //斐波那契数列的实现
    if(n == 0) { 
        return 0; //边界条件
    } else if(n == 1) {
        return 1; //边界条件
    } else {
        return F(n - 1) + F(n - 2); //递归表达式
    }
}

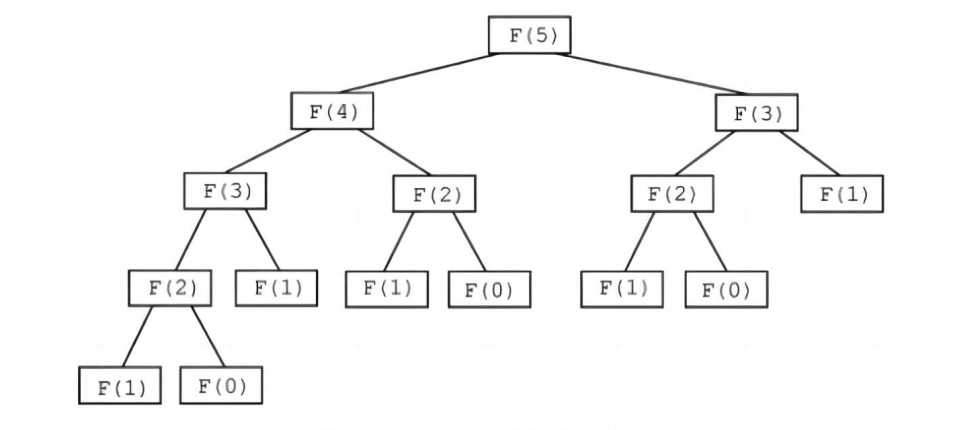
递归调用过程：

队列的应用

1. 二叉树的层次遍历

→ 将根节点入队；每次出队一个节点并访问，将其左右孩子（非空）依次入队，实现按层从左到右遍历。

2. 图的广度优先搜索（BFS）

→ 从起始顶点出发，先访问其所有邻接点（入队），再逐层向外扩展，用于求最短路径（无权图）。

3. 操作系统进程调度（时间片轮转）

→ 就绪进程排成队列，CPU 按顺序分配时间片；未执行完的进程回到队尾，保证公平性。

4. 键盘缓冲区 / 打印任务队列

→ 用户输入或打印请求按到达顺序排队，先来先服务（FIFO），避免数据乱序或丢失。

七、高频考点与真题提示

✅ 必考内容

1. 顺序栈 vs 链栈：谁更容易溢出？谁更灵活？
2. 循环队列判满条件 ：(rear + 1) % MAXSIZE == front
3. 共享栈设计目的：提高空间利用率
4. 稀疏矩阵三元组表示：如何存储？如何还原？

✅ 典型真题

【2020年408】在循环队列中，判断队列满的条件是？
答案 ：(rear + 1) % MAXSIZE == front
【某校自命题】共享栈中，两个栈如何避免冲突？
答案 ：从两端向中间生长，当 top1 + 1 == top2 时栈满
【2021年模拟题】下列哪个不是栈的应用？

A. 函数调用 B. 括号匹配 C. 任务调度 D. 进制转换
答案：C（任务调度是队列应用）