正态分布,又称高斯分布或钟形曲线,是统计学中最重要、最广泛使用的概率分布之一。它不仅在数学和物理学中占据核心地位,也在社会科学、工程技术和生物医学等领域展现出惊人的普遍性。这一分布的发现历程跨越了近两个世纪,从法国数学家棣莫弗在1733年对二项分布的渐近公式研究,到德国数学家高斯在1809年将其应用于天文学误差分析,再到拉普拉斯在1810年将中心极限定理与误差理论结合,最终形成了完整的理论体系 。正态分布之所以如此普遍,是因为它满足了中心极限定理的核心条件------当一个随机变量是由大量微小独立随机因素的叠加结果时,该变量的分布将趋近于正态分布 。这一分布在自然界和社会现象中的广泛应用,使其成为理解随机性与确定性之间关系的桥梁,也是科学和工程领域处理不确定性的基础工具。
一、正态分布的历史发展脉络
正态分布的发现历程始于18世纪的概率论研究。法国数学家棣莫弗(1667-1754)在1733年研究二项分布的渐近公式时,首次提出了正态分布的概率密度函数 。他发现当二项分布的参数 p=12p = \frac{1}{2}p=21 且试验次数 nnn 趋于无穷大时,二项分布可以近似为一种钟形曲线分布 。这一发现最初被应用于赌博问题的解决,但当时并未引起广泛关注。棣莫弗将这一结果告知斯特林(1692-1770),后者补充了斯特林公式 n!≈2πn(n/e)nn! \approx \sqrt{2\pi n}(n/e)^nn!≈2πn (n/e)n,使得计算更加简便 。
真正使正态分布获得广泛应用的是德国数学家高斯(1777-1855)的工作。1809年,高斯在其著作《绕日天体运动的理论》中,独立推导出正态分布的概率密度函数,用于描述天文学测量中的误差分布 。他基于"算术平均值是真值最合理的估计"这一假设,通过最大似然估计法,推导出误差分布必须满足的条件 。高斯的推导过程非常精妙:假设测量误差 ei=xi−θe_i = x_i - \thetaei=xi−θ(其中 xix_ixi 是第 iii 次测量值,θ\thetaθ 是真值),似然函数为 L(θ)=∏i=1nf(xi−θ)L(\theta) = \prod_{i=1}^n f(x_i - \theta)L(θ)=∏i=1nf(xi−θ) 。他要求这个似然函数在 θ=xˉ\theta = \bar{x}θ=xˉ(样本均值)处达到最大值,通过求导并利用函数对称性等条件,最终推导出误差分布函数 f(x)=Me−x2/(2σ2)f(x) = Me^{-x^2/(2\sigma^2)}f(x)=Me−x2/(2σ2),其中 M=1/(σ2π)M = 1/(\sigma\sqrt{2\pi})M=1/(σ2π ) 是归一化常数 。
高斯的工作为正态分布奠定了理论基础,但其论证存在循环性缺陷------他假设算术平均值最优,从而推导出误差分布为正态,又反过来用正态分布的性质证明算术平均值的最优性 。这一缺陷在1810年被拉普拉斯(Pierre-Simon Laplace)解决,他将高斯的正态误差理论与自己发现的中心极限定理联系起来,提出了"元误差学说" 。拉普拉斯指出,如果误差可以看成许多微小独立随机因素的叠加,那么根据中心极限定理,误差的分布必然近似正态分布 。这一解释更加自然合理,为正态分布的广泛应用提供了坚实的理论基础。
1837年,德国数学家海根(G.H. Hagen)进一步完善了元误差学说,但他提出的假设存在局限性:他将误差设想为大量独立同分布的元误差之和,每个元误差仅取两个值,概率各为1/2 。虽然这一假设较为简单,但通过二项分布的极限定理,仍然可以得出误差服从正态分布的结论 。拉普拉斯的理论弥补了高斯论证的循环性缺陷,使正态分布理论成为一个和谐的整体 。
在19世纪,统计学家魁特奈特(A. Quetelet)和高尔顿(Francis Galton)将正态分布推广到其他数据领域 。魁特奈特提出,将一批数据是否能很好地拟合正态分布作为判断该数据是否同质的标准 。高尔顿则通过"高尔顿钉板"实验,直观展示了正态分布的形成机制 。这个装置由竖直木板上的钉子阵列构成,小球从顶部自由下落时,每碰到钉子后向左或向右的概率相等 。当大量小球下落后,最终在底部形成的分布呈现典型的钟形曲线,即正态分布 。这一实验不仅验证了中心极限定理,也解释了为何即使存在显著因素(如遗传),人类身高等指标仍呈现正态分布 。
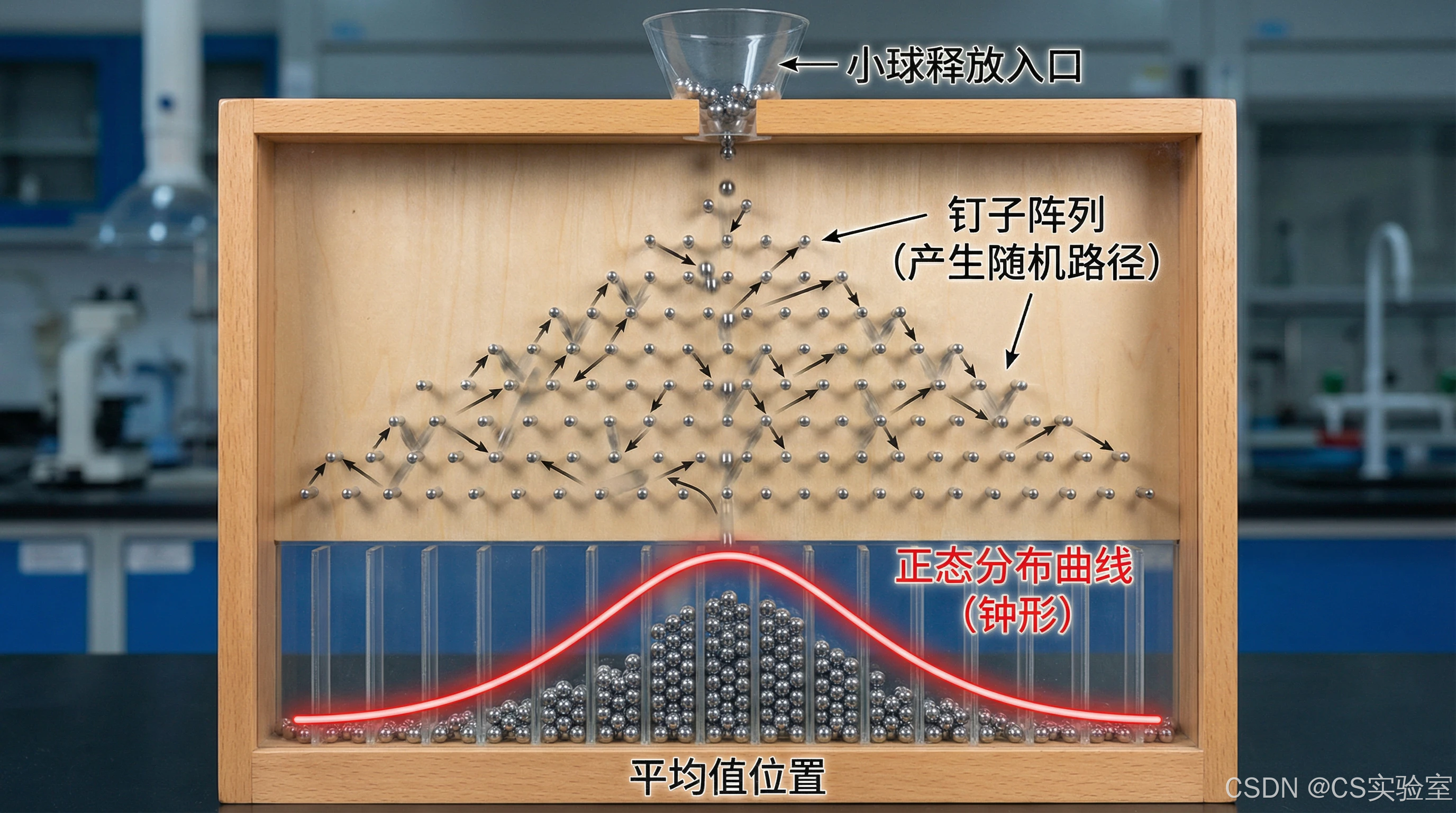
图2:高尔顿钉板实验
二、正态分布的数学本质与核心性质
正态分布的概率密度函数(PDF)是其数学本质的核心表达。对于服从正态分布的随机变量 XXX,其PDF定义为:
f(x)=12πσ2e−(x−μ)22σ2,−∞<x<+∞ f(x) = \frac{1}{\sqrt{2\pi\sigma^2}} e^{-\frac{(x-\mu)^2}{2\sigma^2}}, \quad -\infty < x < +\infty f(x)=2πσ2 1e−2σ2(x−μ)2,−∞<x<+∞
其中,μ\muμ 是分布的均值(位置参数),控制分布的中心位置;σ2\sigma^2σ2 是方差(形状参数),控制分布的宽度 。当 μ=0\mu = 0μ=0 且 σ=1\sigma = 1σ=1 时,分布称为标准正态分布,记为 X∼N(0,1)X \sim N(0,1)X∼N(0,1),其PDF为:
φ(x)=12πe−x2/2 \varphi(x) = \frac{1}{\sqrt{2\pi}} e^{-x^2/2} φ(x)=2π 1e−x2/2
正态分布的数学本质体现在其对称性、单峰性、可标准化性以及与其他分布的关系上 。首先,正态分布曲线关于均值 \\mu 对称,即对于任意 h>0h > 0h>0,有 f(μ+h)=f(μ−h)f(\mu + h) = f(\mu - h)f(μ+h)=f(μ−h) 。其次,曲线在 \\mu 处达到峰值,随着 xxx 离 \\mu 越远,曲线值越小,最终趋近于零但不与横轴相交,形成钟形曲线 。
正态分布的拐点位于 x=μ±σx = \mu \pm \sigmax=μ±σ 处,这是通过计算二阶导数并求其零点得出的 。拐点的存在使得曲线在中心附近增长最快,两侧增长速率逐渐减缓,形成平滑的钟形曲线。这一特性使得正态分布具有良好的数学性质,便于进行积分和微分运算。
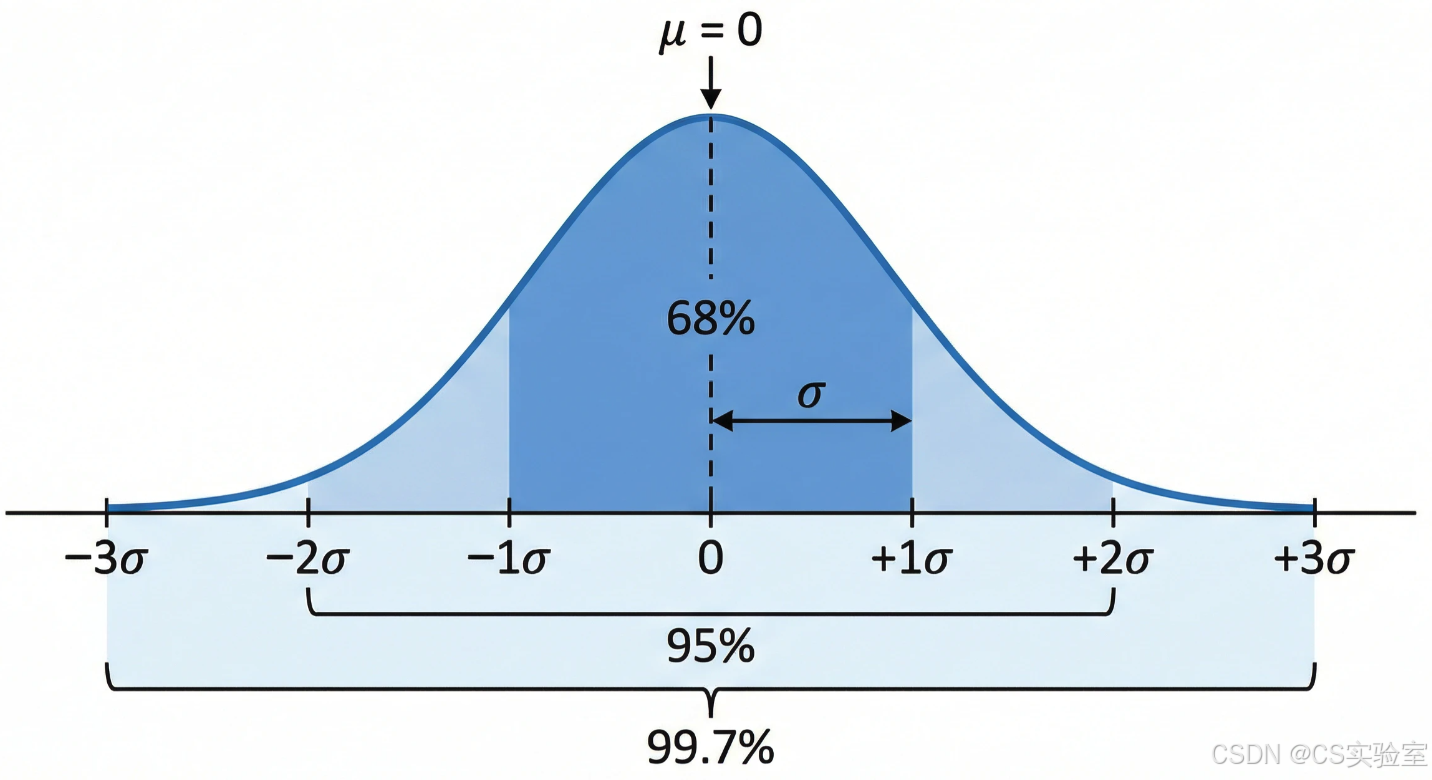
图1:正态分布曲线
正态分布的统计学性质尤为突出。最著名的"68-95-99.7法则"表明,对于标准正态分布 X∼N(0,1)X \sim N(0,1)X∼N(0,1),有:
P(∣X∣≤1)≈68.27%,P(∣X∣≤2)≈95.45%,P(∣X∣≤3)≈99.73% P(|X| \leq 1) \approx 68.27\%, \quad P(|X| \leq 2) \approx 95.45\%, \quad P(|X| \leq 3) \approx 99.73\% P(∣X∣≤1)≈68.27%,P(∣X∣≤2)≈95.45%,P(∣X∣≤3)≈99.73%
对于一般正态分布 X∼N(μ,σ2)X \sim N(\mu, \sigma^2)X∼N(μ,σ2),则有:
P(∣X−μ∣≤σ)≈68.27%,P(∣X−μ∣≤2σ)≈95.45%,P(∣X−μ∣≤3σ)≈99.73% P(|X - \mu| \leq \sigma) \approx 68.27\%, \quad P(|X - \mu| \leq 2\sigma) \approx 95.45\%, \quad P(|X - \mu| \leq 3\sigma) \approx 99.73\% P(∣X−μ∣≤σ)≈68.27%,P(∣X−μ∣≤2σ)≈95.45%,P(∣X−μ∣≤3σ)≈99.73%
这一经验法则为实际应用提供了简便的参考,使得正态分布成为处理不确定性的有力工具。
正态分布的特征函数是其数学本质的另一重要表达。对于 X∼N(μ,σ2)X \sim N(\mu, \sigma^2)X∼N(μ,σ2),其特征函数为:
ϕX(t)=exp(iμt−σ2t22) \phi_X(t) = \exp\left(i\mu t - \frac{\sigma^2 t^2}{2}\right) ϕX(t)=exp(iμt−2σ2t2)
特征函数的乘积性质使得正态分布具有可加性:若 X∼N(μ1,σ12)X \sim N(\mu_1, \sigma_1^2)X∼N(μ1,σ12),Y∼N(μ2,σ22)Y \sim N(\mu_2, \sigma_2^2)Y∼N(μ2,σ22) 且 X 和 YYY 独立,则 X+Y∼N(μ1+μ2,σ12+σ22)X + Y \sim N(\mu_1 + \mu_2, \sigma_1^2 + \sigma_2^2)X+Y∼N(μ1+μ2,σ12+σ22) 。这一性质在工程和物理领域尤为重要,因为它允许将复杂系统分解为多个独立组件,再通过简单加法规则分析整体性能。
正态分布的矩母函数为:
MX(t)=exp(μt+σ2t22) M_X(t) = \exp\left(\mu t + \frac{\sigma^2 t^2}{2}\right) MX(t)=exp(μt+2σ2t2)
矩母函数的二次形式表明,正态分布的三阶及以上矩为零,进一步说明其对称性和有限方差特性 。正态分布的这种数学结构使其成为处理随机变量和的理想模型,这也是中心极限定理的核心结论 。
三、符合正态分布的现象类型及其数学解释
正态分布在自然界和社会现象中展现出惊人的普遍性,主要体现在以下几个方面:
自然现象 :许多自然现象的测量值服从或近似服从正态分布。例如,人体身高、体重、血压等生理指标在同龄同性人群中呈现正态分布 。这是因为个体的身高受到遗传、营养、环境等大量微小独立因素的影响,这些因素的叠加效应符合中心极限定理的条件。同样,理想气体分子的速度分量(vx,vy,vzv_x, v_y, v_zvx,vy,vz)独立服从正态分布 N(0,σ2)N(0, \sigma^2)N(0,σ2),其中 σ2=kT/m\sigma^2 = kT/mσ2=kT/m(kkk 为玻尔兹曼常数,TTT 为温度,mmm 为分子质量) 。虽然三维速度分布 fM(v⃗)f_M(\vec{v})fM(v ) 是三个独立正态分布的乘积,属于多维正态分布,但其模长 v=∣v⃗∣v = |\vec{v}|v=∣v ∣ 服从麦克斯韦-玻尔兹曼分布,这说明正态分布的普遍性不仅体现在单变量上,也体现在多变量系统的分量上 。
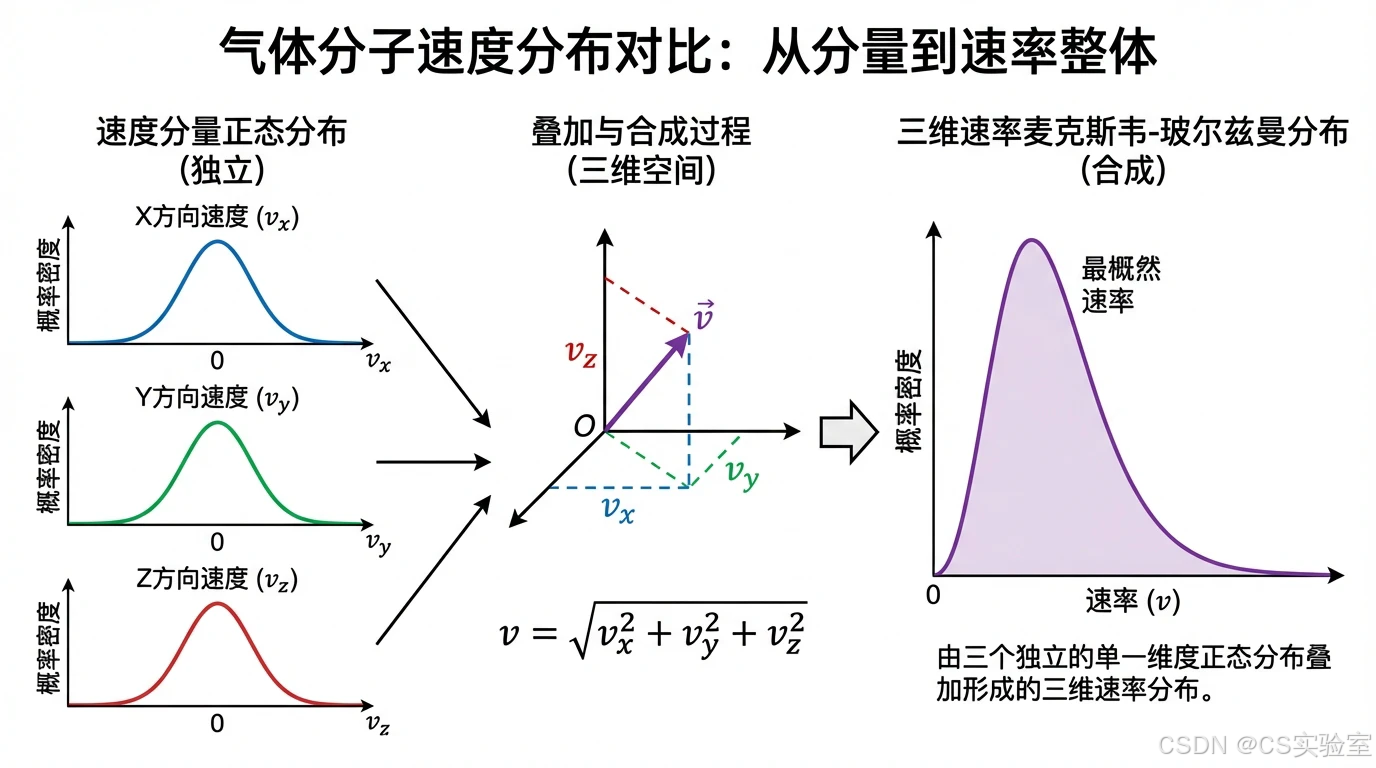
图3:麦克斯韦速度分布与正态分布
社会现象 :许多社会现象的数据也呈现正态分布特征。例如,考试成绩、智力测验分数、收入分布(中低收入部分)等 。以智力测验为例,正常人的智商(IQ)分布以100为中心,标准差为15,形成典型的正态分布 。这是因为智力受到遗传、教育、环境等多方面因素的影响,这些因素的叠加效应符合中心极限定理的条件。不过,需要注意的是,收入分布通常不服从标准正态分布,而是服从对数正态分布------即 ln(X)\ln(X)ln(X) 服从正态分布 。这是因为收入增长往往是相对的,而非绝对的,即收入 XtX_tXt 可以表示为初始收入 X0X_0X0 和一系列增长率 rir_iri 的乘积:Xt=X0∏i=1t(1+ri)X_t = X_0 \prod_{i=1}^t (1 + r_i)Xt=X0∏i=1t(1+ri)。对两边取对数后,log(Xt)=log(X0)+∑i=1tlog(1+ri)\log(X_t) = \log(X_0) + \sum_{i=1}^t \log(1 + r_i)log(Xt)=log(X0)+∑i=1tlog(1+ri),假设增长率 rir_iri 是独立同分布的随机变量,根据中心极限定理,log(Xt)\log(X_t)log(Xt) 将近似服从正态分布,从而 XtX_tXt 服从对数正态分布 。
科学实验与工程应用:在科学实验和工程领域,正态分布被广泛用于描述测量误差和产品质量指标。例如,工程材料的强度、电子元件的参数、通信系统的噪声电压等往往服从正态分布 。这是因为这些指标受到生产过程中的多种微小随机因素的影响,如材料成分波动、加工温度变化、设备精度差异等。在通信系统中,热噪声(如电阻中的电子运动)由大量微小独立扰动叠加而成,根据中心极限定理,其电压分布服从正态分布,形成加性高斯白噪声(AWGN) 。这种噪声模型简化了信号处理分析,使得工程师能够基于正态分布理论设计通信系统。
统计学应用:正态分布是统计学中的基础工具,用于参数估计、假设检验、回归分析等 。许多统计方法(如t检验、Z检验、方差分析等)都基于正态分布假设。这是因为实际数据往往可以通过适当变换近似服从正态分布,或者其样本均值在样本量足够大时近似服从正态分布(根据中心极限定理) 。例如,在医学研究中,基因表达数据通常经过对数转换后近似服从正态分布,便于使用t检验等方法进行差异表达分析 。
符合正态分布的典型案例:
| 现象类型 | 具体案例 | 数学解释 |
|---|---|---|
| 生物指标 | 人体身高、体重、血压等 | 受遗传、营养、环境等大量微小因素影响,符合CLT条件 |
| 物理现象 | 气体分子速度分量、热噪声电压 | 独立微小扰动的叠加,符合CLT条件 |
| 工程质量 | 零件尺寸、纤维纤度、电容器电容量等 | 生产过程中的多种随机因素影响,符合CLT条件 |
| 社会现象 | 考试成绩、智力测验分数等 | 多种因素共同作用,符合CLT条件 |
| 生物学实验 | 基因表达水平(对数转换后) | 测量误差和实验条件波动的叠加,符合CLT条件 |
四、中心极限定理与误差叠加机制
中心极限定理(CLT)是解释正态分布普遍性的核心理论 。CLT指出,当一个随机变量是由大量微小独立随机因素的叠加结果时,该变量的分布将趋近于正态分布,无论这些因素本身的分布如何 。这一定理为正态分布的广泛应用提供了坚实的理论基础。
CLT的数学表述如下:设 X_1, X_2, \\dots, X_n 是独立同分布(i.i.d.)的随机变量序列,具有共同的均值 μ\muμ 和有限方差 σ2\sigma^2σ2。当 n→∞n \to \inftyn→∞ 时,样本均值 Xˉ=1n∑i=1nXi\bar{X} = \frac{1}{n}\sum_{i=1}^n X_iXˉ=n1∑i=1nXi 的分布近似服从正态分布 N(μ,σ2/n)N(\mu, \sigma^2/n)N(μ,σ2/n):
limn→∞P(Xˉ−μσ/n≤x)=Φ(x) \lim_{n \to \infty} P\left( \frac{\bar{X} - \mu}{\sigma/\sqrt{n}} \leq x \right) = \Phi(x) n→∞limP(σ/n Xˉ−μ≤x)=Φ(x)
其中,Φ(x)\Phi(x)Φ(x) 是标准正态分布的累积分布函数(CDF) 。这一定理表明,无论原始数据如何分布,只要满足独立性和有限方差的条件,其均值在样本量足够大时将近似服从正态分布 。
CLT的证明方法多样,其中特征函数法由李雅普诺夫于1900年提出,具有简洁性和一般性 。李雅普诺夫利用特征函数的乘积性质和泰勒展开,证明了独立随机变量和的特征函数收敛于正态分布的特征函数 。这一证明方法降低了CLT的条件要求,扩大了其应用范围。
误差叠加机制是CLT在误差分析中的具体应用。高斯和拉普拉斯认为,测量误差是由大量微小独立因素(元误差)的叠加而成 。海根在1837年提出了更具体的元误差学说:误差可以视为大量独立同分布的元误差之和,每个元误差仅取两个值,概率各为1/2 。通过二项分布的极限定理(棣莫弗-拉普拉斯定理),立即可以得出误差服从正态分布的结论 。
误差叠加的数学机制 可以通过以下步骤理解:假设误差 E=∑i=1neiE = \sum_{i=1}^n e_iE=∑i=1nei,其中 eie_iei 是独立的元误差,具有均值 μe\mu_eμe 和方差 $\sigma_e^2 。根据CLT,当 n→∞n \to \inftyn→∞ 时,误差 EEE 将近似服从正态分布 N(nμe,nσe2)N(n\mu_e, n\sigma_e^2)N(nμe,nσe2)。这一结论表明,即使单个元误差的分布较为复杂,只要满足独立性和有限方差的条件,其总和的分布将趋近于正态分布 。
五、正态分布的局限性与适用条件
尽管正态分布在许多领域展现出惊人的普遍性,但它也存在明显的局限性。这些局限性主要源于中心极限定理的适用条件 ,即当随机变量的和满足以下条件时,CLT才成立:
- 随机变量必须相互独立
- 随机变量必须具有有限的方差
- 随机变量的分布不能具有过重的尾部(即厚尾分布)
当这些条件不满足时,实际分布可能与正态分布存在显著差异。例如,在金融领域,资产收益率的分布通常呈现"肥尾现象"------尾部概率高于正态分布 。这是因为金融市场的收益率受到多种因素影响,包括投资者行为、市场波动等,这些因素可能不满足CLT的独立性和有限方差条件。例如,投资者的羊群效应会导致收益率的非独立性和厚尾分布 。
金融肥尾现象的数学解释可以通过厚尾分布模型来理解。传统正态分布的尾部概率为指数型衰减,而厚尾分布(如t分布、广义误差分布(GED))的尾部概率为幂律型衰减 。厚尾分布的概率密度函数为:
f(x)=12σΓ(1/α)cos(πα/2)(1+∣x−μσ∣α)−(1+α)/α f(x) = \frac{1}{2\sigma\Gamma(1/\alpha)\cos(\pi\alpha/2)} \left(1 + \left|\frac{x - \mu}{\sigma}\right|^\alpha\right)^{-(1+\alpha)/\alpha} f(x)=2σΓ(1/α)cos(πα/2)1(1+ σx−μ α)−(1+α)/α
其中,α\alphaα 控制尾部的厚度,当 α=2\alpha = 2α=2 时,厚尾分布退化为正态分布;当 alpha \< 2 时,尾部更厚,即极端值的概率更高 。这一特性使得金融收益数据的QQ图(如图1所示)与正态分布存在明显差异,特别是在尾部区域 。
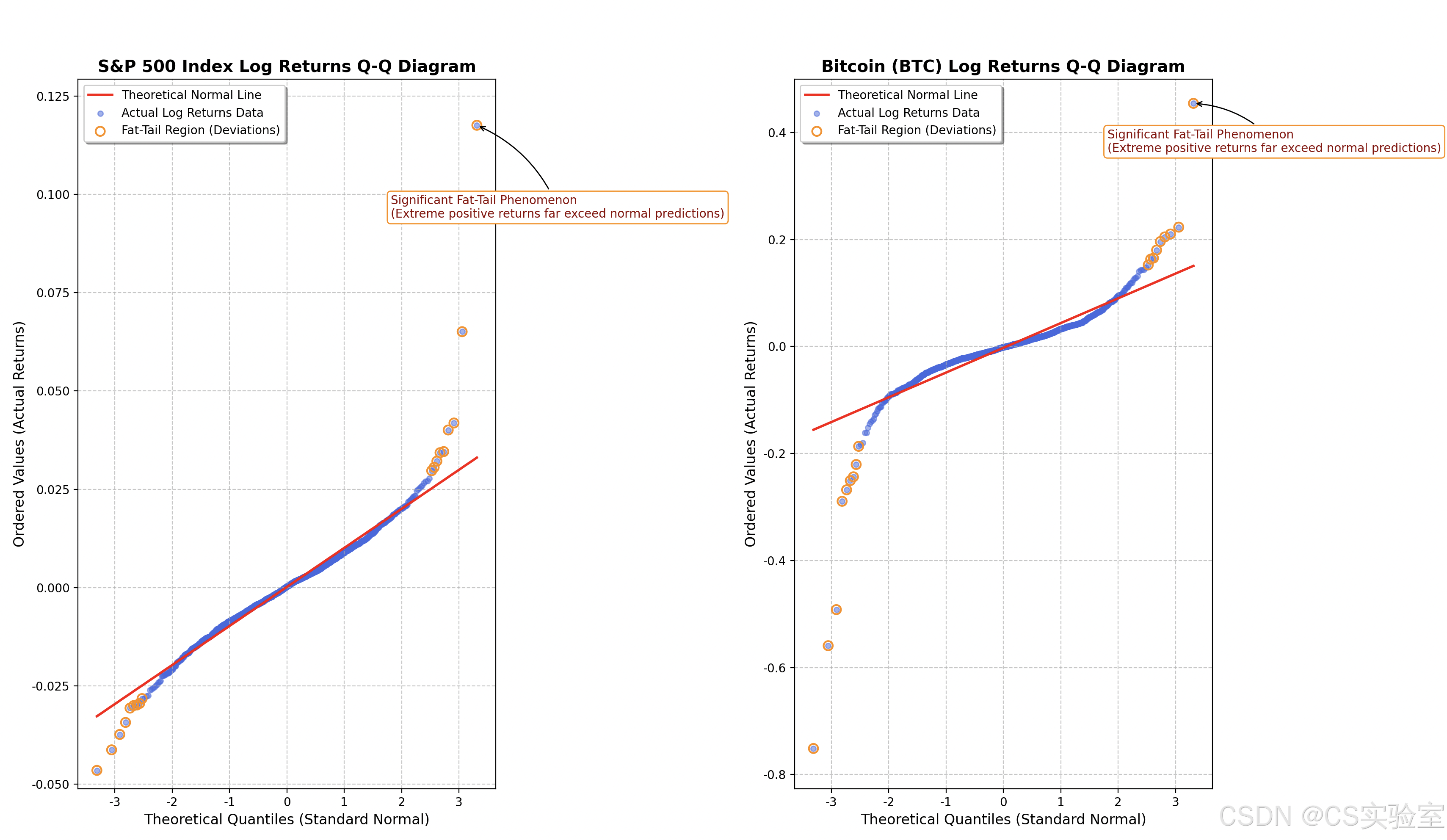
图4:金融收益分布与正态分布对比
六、正态分布的数学推广与应用扩展
正态分布的数学本质使其成为许多重要分布的理论基础。通过对数变换、参数扩展和多维推广,正态分布的应用范围得到了显著扩展 。
对数正态分布是一种重要的推广形式。若随机变量 X 满足 \\ln(X) \\sim N(\\mu, \\sigma\^2) ,则称 X 服从对数正态分布 。其概率密度函数为:
f(x)=1xσ2πexp(−(lnx−μ)22σ2),x>0 f(x) = \frac{1}{x\sigma\sqrt{2\pi}} \exp\left(-\frac{(\ln x - \mu)^2}{2\sigma^2}\right), \quad x > 0 f(x)=xσ2π 1exp(−2σ2(lnx−μ)2),x>0
对数正态分布适用于右偏数据(如收入分布、病毒潜伏期等) 。例如,中国居民收入分布中,中低收入群体的收入分布符合对数正态分布,而高收入群体可能呈现幂律分布 。这是因为收入增长往往是相对的,而非绝对的,即收入 XtX_tXt 可以表示为初始收入 X0X_0X0 和一系列增长率 rir_iri 的乘积:Xt=X0∏i=1t(1+ri)X_t = X_0 \prod_{i=1}^t (1 + r_i)Xt=X0∏i=1t(1+ri)。对两边取对数后,log(Xt)=log(X0)+∑i=1tlog(1+ri)\log(X_t) = \log(X_0) + \sum_{i=1}^t \log(1 + r_i)log(Xt)=log(X0)+∑i=1tlog(1+ri),假设增长率 rir_iri 是独立同分布的随机变量,根据中心极限定理,log(Xt)\log(X_t)log(Xt) 将近似服从正态分布,从而 XtX_tXt 服从对数正态分布 。
多维正态分布是另一重要推广。若 ddd-维随机向量 X⃗\vec{X}X 的概率密度函数为:
f(x⃗)=1(2π)d/2∣Σ∣1/2exp(−12(x⃗−μ⃗)TΣ−1(x⃗−μ⃗)) f(\vec{x}) = \frac{1}{(2\pi)^{d/2} |\Sigma|^{1/2}} \exp\left(-\frac{1}{2} (\vec{x} - \vec{\mu})^T \Sigma^{-1} (\vec{x} - \vec{\mu})\right) f(x )=(2π)d/2∣Σ∣1/21exp(−21(x −μ )TΣ−1(x −μ ))
其中,μ⃗\vec{\mu}μ 是均值向量,Σ\SigmaΣ 是协方差矩阵,则称 X⃗\vec{X}X 服从 ddd-维正态分布 。多维正态分布具有许多良好的性质,如边缘分布仍为正态分布,线性变换后的分布仍为正态分布等 。这些性质使得多维正态分布在工程和物理领域得到广泛应用,如通信系统的多维噪声分析、材料强度的多变量建模等。
七、正态分布的深层哲学意义
正态分布的普遍性不仅具有数学意义,也具有深刻的哲学意义。它反映了自然界和社会现象中的一种基本规律------复杂系统的涌现行为往往呈现出简单而优美的分布模式。
这一现象可以从信息论的角度解释。正态分布是满足均值和方差约束下的最大熵分布,即在给定均值和方差条件下,正态分布包含了最多的不确定性,或者说信息熵最大 。这意味着,当一个系统受到大量微小独立因素影响时,其分布将自然趋近于正态分布,因为这是系统在给定约束下最可能的分布。
从物理学的角度看,正态分布的普遍性也体现了能量分布的均衡性。例如,麦克斯韦-玻尔兹曼分布表明,气体分子的速度分量独立服从正态分布,这是因为分子在热运动中不断与周围分子碰撞,每次碰撞都会改变其速度分量,这些微小的改变累积起来形成了正态分布 。
从社会学的角度看,正态分布的普遍性反映了社会系统的复杂性和均衡性。例如,人类身高、体重等生理指标的分布呈现正态分布,这是因为个体受到遗传、营养、环境等多种因素的影响,这些因素的综合效应形成了均衡的分布 。
八、正态分布的未来研究方向
尽管正态分布已经被广泛研究和应用,但其理论和应用仍有许多值得探索的方向。随着大数据和人工智能的发展,正态分布的理论框架正在与现代技术相结合,形成新的研究领域。
在理论方面,非高斯正态分布的研究正在兴起。例如,分数阶正态分布、量子正态分布等,这些研究扩展了正态分布的数学框架,使其能够更好地描述复杂系统的特性。
在应用方面,正态分布与机器学习的结合正在成为热点。例如,高斯过程回归、变分自编码器等,这些方法利用正态分布的数学性质,处理高维数据和不确定性建模。
在工程领域,正态分布的假设正在被重新审视。例如,在通信系统中,非高斯噪声模型(如莱维噪声、脉冲噪声)正在被研究,以更好地描述实际系统的性能。
九、结语
正态分布从数学发现到自然法则的演变,体现了人类对随机性理解的深化。这一分布的普遍性源于中心极限定理的核心机制------大量微小独立因素的叠加效应 。无论是在自然现象、社会现象,还是科学实验和统计学应用中,正态分布都展现出了惊人的适用性 。
然而,正态分布的局限性也提醒我们,在处理复杂系统时,不能盲目依赖正态分布假设,而应根据具体情况进行适当调整和扩展。通过对数正态分布、厚尾分布等模型的研究,我们可以更准确地描述和预测各种现象。
正态分布的历史发展脉络,从棣莫弗的发现,到高斯的应用,再到拉普拉斯的理论完善,以及20世纪的进一步推广,展现了数学与科学的互动与融合 。这一分布不仅是统计学的基础工具,也是理解自然界和社会现象复杂性的窗口 。在未来的研究中,正态分布的理论框架将继续与现代技术相结合,为我们提供更强大的工具来处理不确定性和复杂性。
附录
生成 图 4 对应的代码如下:
python
import numpy as np
import matplotlib.pyplot as plt
from scipy import stats
import matplotlib
# --- Data Simulation ---
# To demonstrate the fat-tail phenomenon, we use the Student's t-distribution to simulate financial asset returns.
# The t-distribution has thicker tails than the normal distribution. The smaller the degrees of freedom (df), the thicker the tails.
np.random.seed(42) # Ensure reproducibility
n_samples = 1500 # Number of samples
# 1. Simulate S&P 500: A relatively mature market with lower volatility and less extreme tails compared to cryptocurrencies
# Using a t-distribution with df=5 and smaller scale
sp500_log_returns = stats.t.rvs(df=5, loc=0.0003, scale=0.008, size=n_samples)
# 2. Simulate Bitcoin (BTC): A high-volatility market with extreme fat-tail phenomenon
# Using a t-distribution with df=2.5 (very thick tails) and larger scale
btc_log_returns = stats.t.rvs(df=2.5, loc=0.0005, scale=0.025, size=n_samples)
# --- Plotting ---
fig, axes = plt.subplots(1, 2, figsize=(16, 7))
def plot_qq_with_fat_tail_highlight(ax, data, title):
"""
Plot a Q-Q diagram with highlighted fat-tail regions
"""
# Calculate theoretical quantiles and ordered values for the Q-Q plot
# stats.probplot defaults to comparing against the standard normal distribution
(osm, osr), (slope, intercept, r) = stats.probplot(data, dist="norm", plot=None)
# 1. Plot the theoretical normal distribution line (red solid line)
# This line represents where points should lie if the data perfectly follows a normal distribution
ax.plot(osm, slope * osm + intercept, color='red', linestyle='-', linewidth=2, label='Theoretical Normal Line')
# 2. Plot the actual data points (blue scatter points)
ax.scatter(osm, osr, color='royalblue', alpha=0.5, s=20, label='Actual Log Returns Data')
# 3. Highlight the fat-tail regions (extreme ends deviating from the line)
# Select extreme regions where the absolute value of theoretical quantiles exceeds 2.5
threshold = 2.5
tail_mask = np.abs(osm) > threshold
ax.scatter(osm[tail_mask], osr[tail_mask], color='none', edgecolor='darkorange', s=60, linewidth=1.5, zorder=3, label='Fat-Tail Region (Deviations)')
# Add annotation pointing to the upper-right tail
if np.any(osm > threshold):
# Find a representative point in the right tail
idx = np.argmax(osm)
ax.annotate('Significant Fat-Tail Phenomenon\n(Extreme positive returns far exceed normal predictions)',
xy=(osm[idx], osr[idx]),
xytext=(osm[idx]-1.5, osr[idx]*0.8),
arrowprops=dict(facecolor='black', arrowstyle='->', connectionstyle="arc3,rad=.2"),
fontsize=10, color='darkred', bbox=dict(boxstyle="round,pad=0.3", fc="white", ec="darkorange", lw=1))
# Chart decorations
ax.set_title(title, fontsize=14, fontweight='bold')
ax.set_xlabel('Theoretical Quantiles (Standard Normal)', fontsize=12)
ax.set_ylabel('Ordered Values (Actual Returns)', fontsize=12)
ax.legend(loc='upper left', frameon=True, shadow=True)
ax.grid(True, linestyle='--', alpha=0.7)
# Adjust axis limits to better display tails
ax.set_ylim(bottom=min(osr)*1.1, top=max(osr)*1.1)
# Plot S&P 500 Q-Q diagram
plot_qq_with_fat_tail_highlight(axes[0], sp500_log_returns, 'S&P 500 Index Log Returns Q-Q Diagram')
# Plot Bitcoin Q-Q diagram
plot_qq_with_fat_tail_highlight(axes[1], btc_log_returns, 'Bitcoin (BTC) Log Returns Q-Q Diagram')
# Add overall title
fig.suptitle('Comparative Analysis: Q-Q Diagrams and Fat-Tail Phenomenon of Bitcoin vs. S&P 500 Returns', fontsize=18, y=1.02)
plt.tight_layout()
# Display the chart
plt.show()