课程表系列（LeetCode 207 & 210 & 630 & 1462）

氷泠2026-01-09 9:55

1 概述

本文会介绍课程表系列的题目，包括思路以及详细代码。

2 课程表1

2.1 原题

2.2 思路

课程表本质上就是求有向图中有没有环的题目，有环就无解，无环就有解。

而求有没有环的一个经典方法，就是拓扑排序。

拓扑排序是有向无环图的一种线性排序，使得对于图中每一条有向边u->v，节点u的排序都出现在节点v的前面。具体做法：

  • 计算每个节点的入度，也就是有多少个节点指向该节点
  • 将所有入度为0的节点加入队列
  • 遍历该节点的邻居，将其入度减1
  • 若邻居入度为0，将其入队
  • 重复直到队列为空
  • 统计入度数组，如果每个数值都为0，表示没有环，否则有环

拓扑排序动图示例如下：

代码如下：

cpp 复制代码 
class Solution {
public:
    bool canFinish(int numCourses, vector<vector<int> > &prerequisites) {
        // 节点队列
        queue<int> q;
        // 入度数组
        vector in_degree(numCourses, 0);
        // 邻接表
        vector graph(numCourses, vector<int>());
        for (auto &p: prerequisites) {
            // 统计入度
            ++in_degree[p[0]];
            // 构建图，主要这里只需要存储p[1]->p[0]即可，有向图
            graph[p[1]].push_back(p[0]);
        }
        for (int i = 0; i < numCourses; ++i) {
            // 判断哪个节点入度为0
            if (in_degree[i] == 0) {
                // 如果入度为0就入队
                q.push(i);
            }
        }
        // 不断遍历队列直到为空
        while (!q.empty()) {
            // 获取当前队列的大小
            const int q_size = static_cast<int>(q.size());
            // 遍历队列
            for (int i = 0; i < q_size; ++i) {
                // 拿到当前节点
                const int front = q.front();
                // 出队
                q.pop();
                // 遍历当前节点的邻居
                for (int v: graph[front]) {
                    // 入度减1
                    --in_degree[v];
                    // 如果入度为0，入队
                    if (in_degree[v] == 0) {
                        q.push(v);
                    }
                }
            }
        }
        // 判断入度为0的个数是否等于节点总数，等于表示没有环，否则有环
        return ranges::count(in_degree, 0) == numCourses;
    }
}

2.3 三色标记法

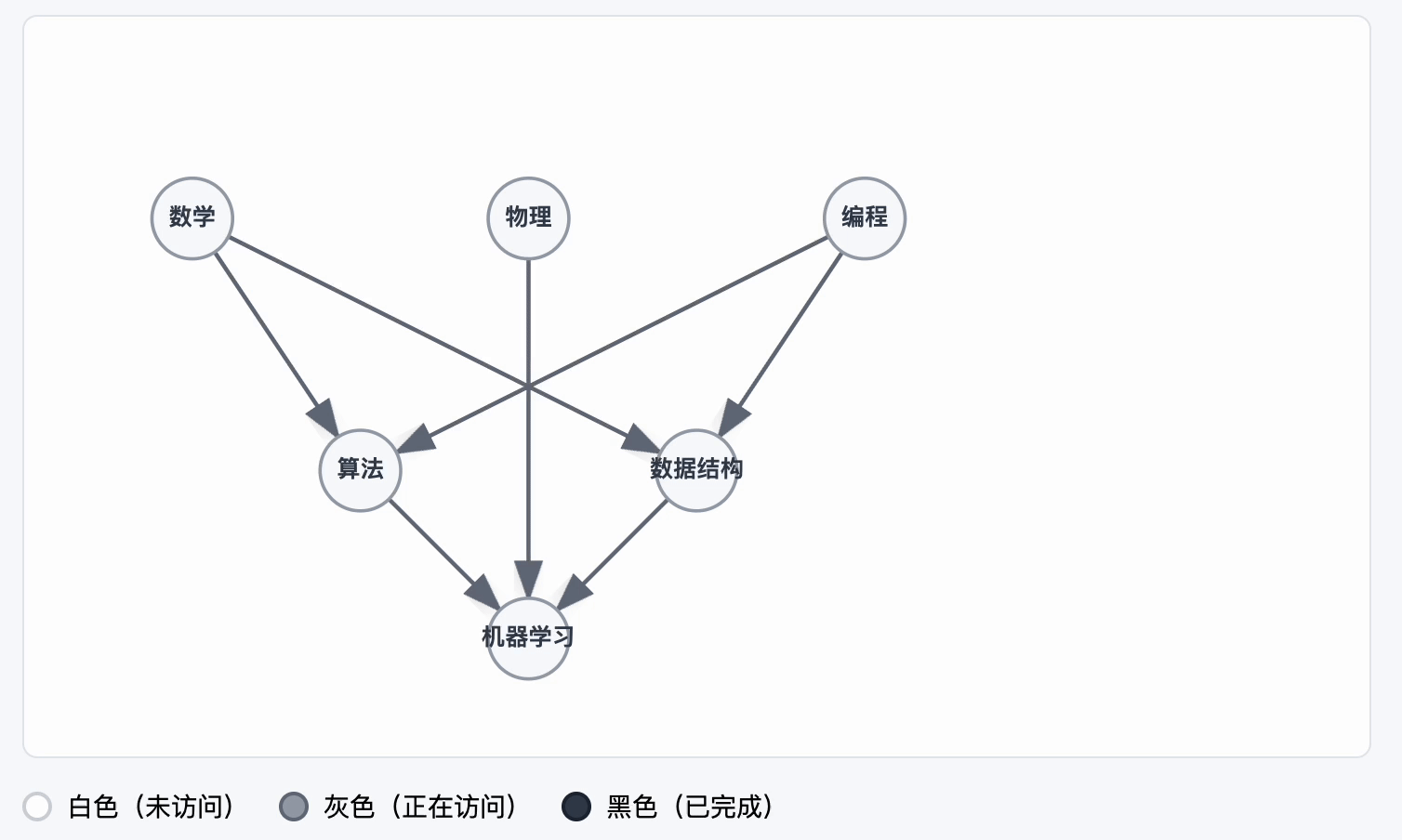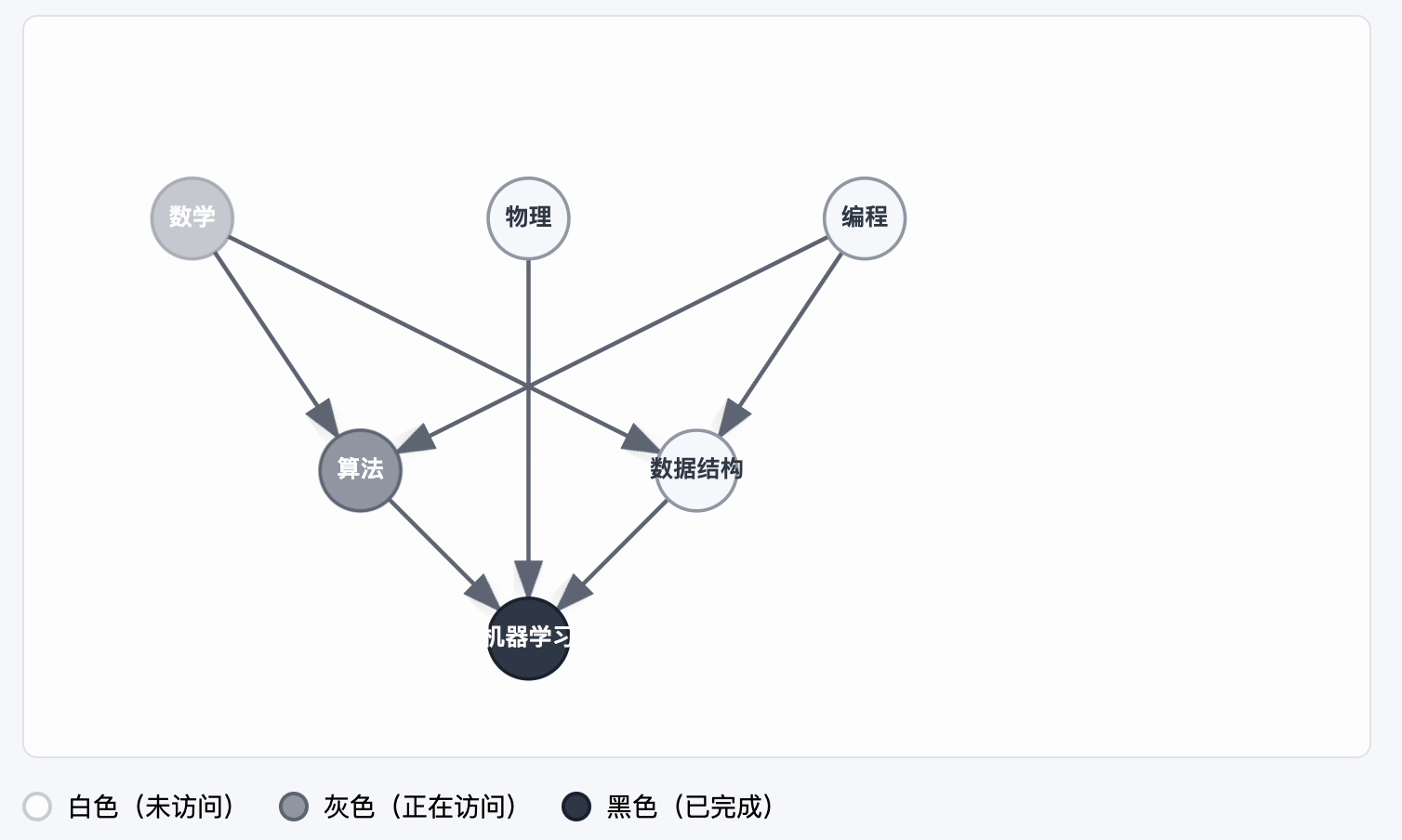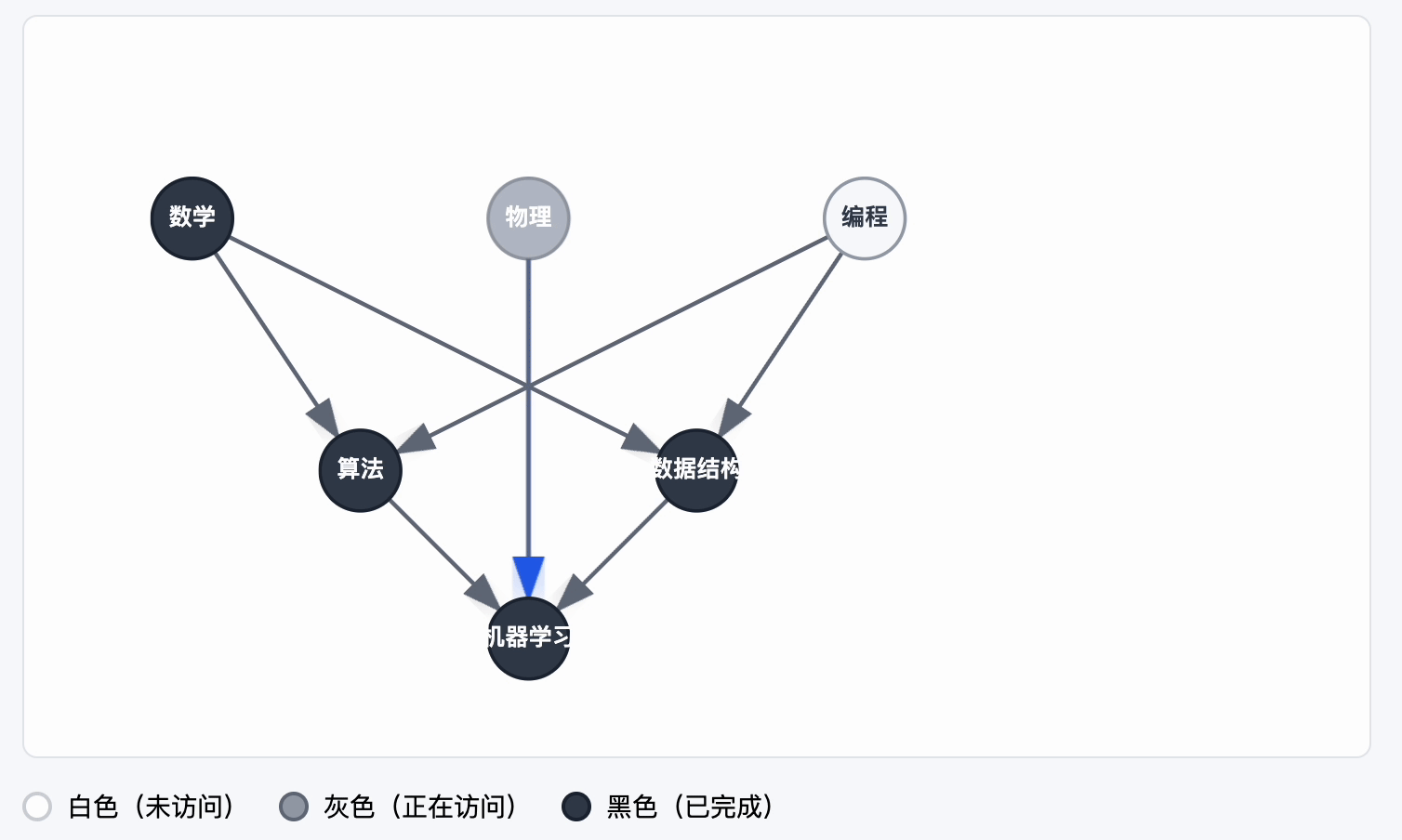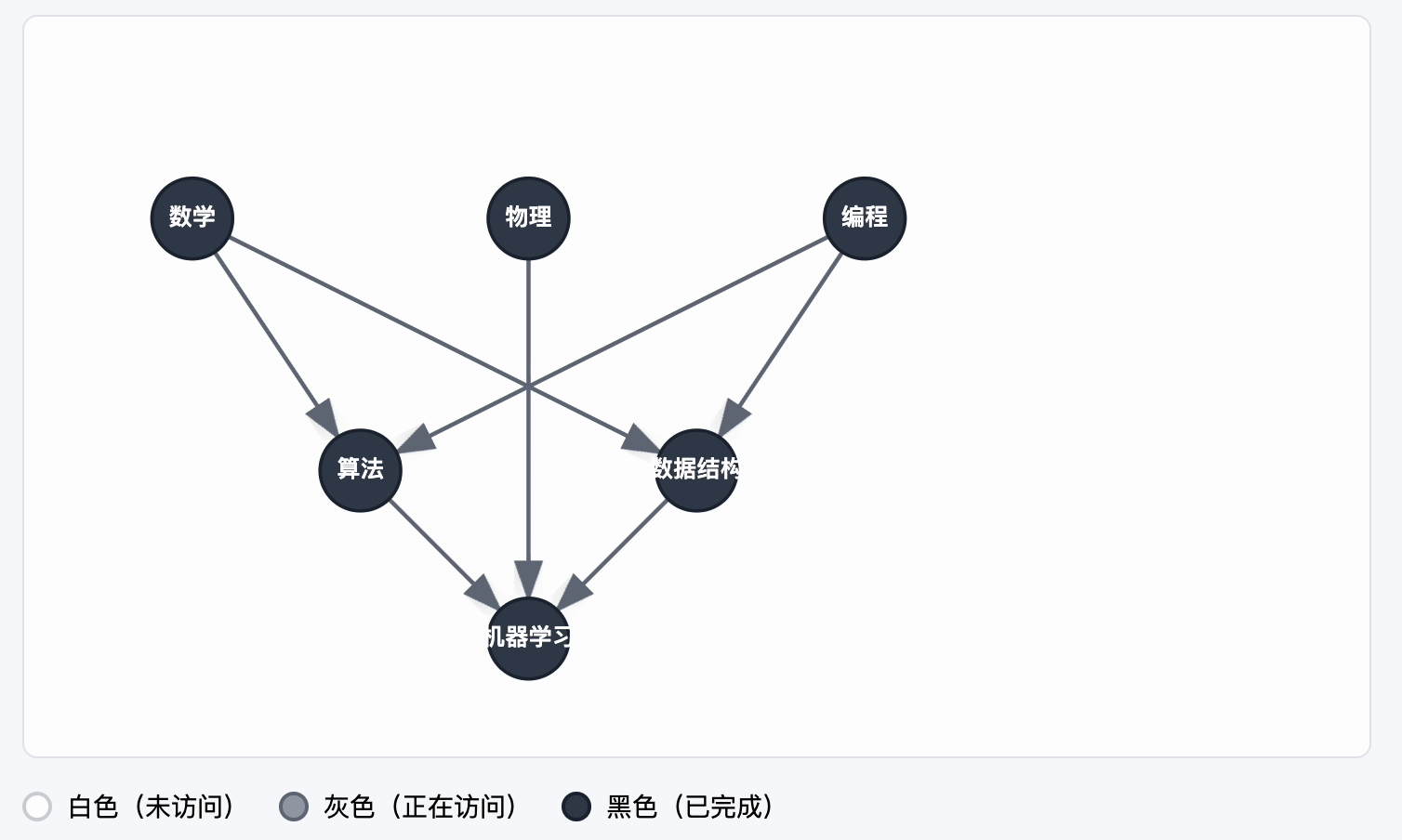
另一种判断有没有环的方法，就是三色标记法。

三色标记法的原理是将所有节点都标记三种颜色之一：

  • 白色：未访问
  • 灰色：正在访问
  • 黑色：已访问完成

如果在DFS过程中遇到了一个灰色的节点的，表明节点有环。

具体思路：

  • 所有节点初始化成白色
  • 对每个白色节点进行DFS
  • 进入节点时标记为灰色，退出时标记为黑色
  • 如果当前节点的邻居时碰到了灰色节点，表明有环

动图示例：

代码如下：

cpp 复制代码 
class Solution {
public:
    bool canFinish(int numCourses, vector<vector<int> > &prerequisites) {
        vector graph(numCourses, vector<int>());
        for (auto &p: prerequisites) {
            // 构建图，主要这里只需要存储p[1]->p[0]即可，有向图
            graph[p[1]].push_back(p[0]);
        }
        // 0表示白色，1表示灰色，2表示黑色
        vector color(numCourses, 0);
        // 表示是否有环
        bool cycle = false;
        auto dfs = [&](this auto &&dfs, int node) {
            // 如果有环直接返回
            if (cycle) {
                return;
            }
            // 当前节点标记灰色
            color[node] = 1;
            // 遍历邻居
            for (const int v: graph[node]) {
                // 如果邻居是白色
                if (color[v] == 0) {
                    // 访问
                    dfs(v);
                } else if (color[v] == 1) {
                    // 如果是灰色，表示有环，返回
                    cycle = true;
                    return;
                }
            }
            // 遍历完所有邻居后，当前节点标记黑色
            color[node] = 2;
        };
        // 遍历所有白色节点
        for (int i = 0; i < numCourses; ++i) {
            if (color[i] == 0) {
                dfs(i);
            }
        }
        // 没有环返回true
        return !cycle;
    }
};

2.4 Java版本

2.4.1 拓扑排序

java 复制代码 
import java.util.*;

public class Solution {
    public boolean canFinish(int numCourses, int[][] prerequisites) {
        LinkedList<Integer> q = new LinkedList<>();
        int[] inDegree = new int[numCourses];
        List<List<Integer>> list = new ArrayList<>();
        for (int i = 0; i < numCourses; i++) {
            list.add(new ArrayList<>());
        }
        for (int[] p : prerequisites) {
            ++inDegree[p[0]];
            list.get(p[1]).add(p[0]);
        }
        for (int i = 0; i < numCourses; i++) {
            if (inDegree[i] == 0) {
                q.addLast(i);
            }
        }
        while (!q.isEmpty()) {
            int size = q.size();
            for (int i = 0; i < size; i++) {
                int front = q.pollFirst();
                for (int v : list.get(front)) {
                    if (--inDegree[v] == 0) {
                        q.addLast(v);
                    }
                }
            }
        }
        for (int i = 0; i < numCourses; i++) {
            if(inDegree[i] != 0) {
                return false;
            }
        }
        return true;
    }
}

2.4.2 三色标记

java 复制代码 
import java.util.*;

public class Solution {
    private final List<List<Integer>> list = new ArrayList<>();
    private int[] color;
    private boolean cycle;

    private void dfs(int node) {
        if (cycle) {
            return;
        }
        color[node] = 1;
        for (int v : list.get(node)) {
            if (color[v] == 0) {
                dfs(v);
            } else if (color[v] == 1) {
                cycle = true;
                return;
            }
        }
        color[node] = 2;
    }

    public boolean canFinish(int numCourses, int[][] prerequisites) {
        for (int i = 0; i < numCourses; i++) {
            list.add(new ArrayList<>());
        }
        for (int[] p : prerequisites) {
            list.get(p[1]).add(p[0]);
        }
        color = new int[numCourses];
        for (int i = 0; i < numCourses; i++) {
            if (color[i] == 0) {
                dfs(i);
            }
        }
        return !cycle;
    }
}

2.5 Go版本

2.5.1 拓扑排序

go 复制代码 
func canFinish(numCourses int, prerequisites [][]int) bool {
	q, inDegree, graph := make([]int, 0), make([]int, numCourses), make([][]int, numCourses)
	for i := range graph {
		graph[i] = make([]int, 0)
	}
	for _, p := range prerequisites {
		inDegree[p[0]]++
		graph[p[1]] = append(graph[p[1]], p[0])
	}
	for i := 0; i < numCourses; i++ {
		if inDegree[i] == 0 {
			q = append(q, i)
		}
	}
	for len(q) > 0 {
		qLen := len(q)
		for i := 0; i < qLen; i++ {
			front := q[0]
			q = q[1:]
			for _, v := range graph[front] {
				inDegree[v]--
				if inDegree[v] == 0 {
					q = append(q, v)
				}
			}
		}
	}
	for i := 0; i < numCourses; i++ {
		if inDegree[i] != 0 {
			return false
		}
	}
	return true
}

2.5.2 三色标记

go 复制代码 
func canFinish(numCourses int, prerequisites [][]int) bool {
	graph, color, cycle := make([][]int, numCourses), make([]int, numCourses), false
	for i := range graph {
		graph[i] = make([]int, 0)
	}
	for _, p := range prerequisites {
		graph[p[1]] = append(graph[p[1]], p[0])
	}
	var dfs = func(int) {}
	dfs = func(node int) {
		if cycle {
			return
		}
		color[node] = 1
		for _, v := range graph[node] {
			if color[v] == 0 {
				dfs(v)
			} else if color[v] == 1 {
				cycle = true
				return
			}
		}
		color[node] = 2
	}
	for i := 0; i < numCourses; i++ {
		if color[i] == 0 {
			dfs(i)
		}
	}
	return !cycle
}

3 课程表2

3.1 原题

3.2 思路

这道题和课程表1本质上是一样的，只是在拓扑排序的时候，将节点存储起来就可以了。

具体来说，就是在入队的时候，存储当前节点。因为入队的节点入度已经是0了，直接存储即可，也符合题目的没有顺序要求。

cpp 复制代码 
class Solution {
public:
    vector<int> findOrder(int numCourses, vector<vector<int> > &prerequisites) {
        // 存储
        vector<int> res;
        // 节点队列
        queue<int> q;
        // 入度数组
        vector in_degree(numCourses, 0);
        // 邻接表
        vector graph(numCourses, vector<int>());
        for (auto &p: prerequisites) {
            // 统计入度
            ++in_degree[p[0]];
            // 构建图，主要这里只需要存储p[1]->p[0]即可，有向图
            graph[p[1]].push_back(p[0]);
        }
        for (int i = 0; i < numCourses; ++i) {
            // 判断哪个节点入度为0
            if (in_degree[i] == 0) {
                // 存储结果
                res.push_back(i);
                // 如果入度为0就入队
                q.push(i);
            }
        }
        // 不断遍历队列直到为空
        while (!q.empty()) {
            // 获取当前队列的大小
            const int q_size = static_cast<int>(q.size());
            // 遍历队列
            for (int i = 0; i < q_size; ++i) {
                // 拿到当前节点
                const int front = q.front();
                // 出队
                q.pop();
                // 遍历当前节点的邻居
                for (int v: graph[front]) {
                    // 入度减1
                    --in_degree[v];
                    // 如果入度为0，入队
                    if (in_degree[v] == 0) {
                        // 入队的时候存储结果
                        res.push_back(v);
                        q.push(v);
                    }
                }
            }
        }
        // 判断入度为0的个数是否等于节点总数，等于表示没有环，否则有环
        return ranges::count(in_degree, 0) == numCourses ? res : vector<int>();
    }
};

3.3 三色标记法

同样道理也能用三色标记法解决。

具体做法就是在遍历完成节点，将节点染成黑色的时候，加入结果集。

这样的话结果集相当于是逆向加入的，最后返回的时候需要反转一下，其他代码与课程表1一致。

cpp 复制代码 
class Solution {
public:
    vector<int> findOrder(int numCourses, vector<vector<int> > &prerequisites) {
        // 存储结果
        vector<int> res;
        vector graph(numCourses, vector<int>());
        for (auto &p: prerequisites) {
            // 构建图，主要这里只需要存储p[1]->p[0]即可，有向图
            graph[p[1]].push_back(p[0]);
        }
        // 0表示白色，1表示灰色，2表示黑色
        vector color(numCourses, 0);
        // 表示是否有环
        bool cycle = false;
        auto dfs = [&](this auto &&dfs, int node) {
            // 如果有环直接返回
            if (cycle) {
                return;
            }
            // 当前节点标记灰色
            color[node] = 1;
            // 遍历邻居
            for (const int v: graph[node]) {
                // 如果邻居是白色
                if (color[v] == 0) {
                    // 访问
                    dfs(v);
                } else if (color[v] == 1) {
                    // 如果是灰色，表示有环，返回
                    cycle = true;
                    return;
                }
            }
            // 遍历完所有邻居后，加入结果集
            res.push_back(node);
            // 当前节点标记黑色
            color[node] = 2;
        };
        // 遍历所有白色节点
        for (int i = 0; i < numCourses; ++i) {
            if (color[i] == 0) {
                dfs(i);
            }
        }
        // 反转结果集
        ranges::reverse(res);
        return cycle ? vector<int>() : res;
    }
};

3.4 Java版本

3.4.1 拓扑排序

java 复制代码 
import java.util.*;

public class Solution {
    public int[] findOrder(int numCourses, int[][] prerequisites) {
        List<Integer> res = new ArrayList<>();
        LinkedList<Integer> q = new LinkedList<>();
        int[] inDegree = new int[numCourses];
        List<List<Integer>> list = new ArrayList<>();
        for (int i = 0; i < numCourses; i++) {
            list.add(new ArrayList<>());
        }
        for (int[] p : prerequisites) {
            ++inDegree[p[0]];
            list.get(p[1]).add(p[0]);
        }
        for (int i = 0; i < numCourses; i++) {
            if (inDegree[i] == 0) {
                res.add(i);
                q.addLast(i);
            }
        }
        while (!q.isEmpty()) {
            int size = q.size();
            for (int i = 0; i < size; i++) {
                int front = q.pollFirst();
                for (int v : list.get(front)) {
                    if (--inDegree[v] == 0) {
                        res.add(v);
                        q.addLast(v);
                    }
                }
            }
        }
        for (int i = 0; i < numCourses; i++) {
            if (inDegree[i] != 0) {
                return new int[]{};
            }
        }
        return res.stream().mapToInt(i -> i).toArray();
    }
}

3.4.2 三色标记法

java 复制代码 
import java.util.*;

public class Solution {
    private final List<List<Integer>> list = new ArrayList<>();
    private int[] color;
    private boolean cycle;
    private final List<Integer> res = new ArrayList<>();

    private void dfs(int node) {
        if (cycle) {
            return;
        }
        color[node] = 1;
        for (int v : list.get(node)) {
            if (color[v] == 0) {
                dfs(v);
            } else if (color[v] == 1) {
                cycle = true;
                return;
            }
        }
        res.add(node);
        color[node] = 2;
    }

    public int[] findOrder(int numCourses, int[][] prerequisites) {
        for (int i = 0; i < numCourses; i++) {
            list.add(new ArrayList<>());
        }
        for (int[] p : prerequisites) {
            list.get(p[1]).add(p[0]);
        }
        color = new int[numCourses];
        for (int i = 0; i < numCourses; i++) {
            if (color[i] == 0) {
                dfs(i);
            }
        }
        Collections.reverse(res);
        return cycle ? new int[]{} : res.stream().mapToInt(i -> i).toArray();
    }
}

3.5 Go版本

3.5.1 拓扑排序

go 复制代码 
func findOrder(numCourses int, prerequisites [][]int) []int {
	q, inDegree, graph, res := make([]int, 0), make([]int, numCourses), make([][]int, numCourses), make([]int, 0)
	for i := range graph {
		graph[i] = make([]int, 0)
	}
	for _, p := range prerequisites {
		inDegree[p[0]]++
		graph[p[1]] = append(graph[p[1]], p[0])
	}
	for i := 0; i < numCourses; i++ {
		if inDegree[i] == 0 {
			res, q = append(res, i), append(q, i)
		}
	}
	for len(q) > 0 {
		qLen := len(q)
		for i := 0; i < qLen; i++ {
			front := q[0]
			q = q[1:]
			for _, v := range graph[front] {
				inDegree[v]--
				if inDegree[v] == 0 {
					res, q = append(res, v), append(q, v)
				}
			}
		}
	}
	for i := 0; i < numCourses; i++ {
		if inDegree[i] != 0 {
			return []int{}
		}
	}
	return res
}

3.5.2 三色标记法

go 复制代码 
func findOrder(numCourses int, prerequisites [][]int) []int {
	graph, color, cycle, res := make([][]int, numCourses), make([]int, numCourses), false, make([]int, 0)
	for i := range graph {
		graph[i] = make([]int, 0)
	}
	for _, p := range prerequisites {
		graph[p[1]] = append(graph[p[1]], p[0])
	}
	var dfs = func(int) {}
	dfs = func(node int) {
		if cycle {
			return
		}
		color[node] = 1
		for _, v := range graph[node] {
			if color[v] == 0 {
				dfs(v)
			} else if color[v] == 1 {
				cycle = true
				return
			}
		}
		res = append(res, node)
		color[node] = 2
	}
	for i := 0; i < numCourses; i++ {
		if color[i] == 0 {
			dfs(i)
		}
	}
	if cycle {
		return []int{}
	}
	slices.Reverse(res)
	return res
}

4 课程表3

4.1 原题

4.2 思路

课程表3的话就和环没有什么关系了，求的是最多能修多少门课。

首先看看范围，10^4，意味着基本上就是O(n)或者O(n log n)的解法，O(n^2)的做法可以放弃了。

相比起普通的课程，每门课程都带了一个最后截止时间，这个截止时间意味着：

  • 如果当前的天数大于这个时间，修不了
  • 如果当前天数小于这个时间，但是修了这门课程之后，天数大于截止时间，也修不了

因为每门课程都是等价的，如果想要修尽可能多的课程，那么最后截止时间越早，应该越提前修。

所以，一个简单的思路就是，将课程按照截止时间排序， 贪心修截止时间早的课程。

例子里面的：

bash 复制代码 
[[100, 200], [200, 1300], [1000, 1250], [2000, 3200]]

排序后就变成

bash 复制代码 
[[100, 200],[1000, 1250], [200, 1300] [2000, 3200]]

按顺序修了前3门课，就是结果值3。

但是如果给出的课程如下（已按照截止时间排序）：

bash 复制代码 
[[1,5],[6,8],[2,9],[3,10]]

按照上面的思路只能修[1,5]+[6,8]两门课程，而实际上，可以修[1,5]+[2,9]+[3,10]三门课程。

问题就在于，当修完[6,8]之后，没有修[2,9]，第三门课程[2,9]是一个更好的选择。

为了处理这种类型的问题，就需要把之前贪心的结果[6,8]去掉，而选择一个更好的选择[2,9]。

这种做法就叫反悔贪心。

本质上来说，就是修完当前课程之后，如果发现时间超过了截止时间，就把之前持续时间最大的一门课程反悔掉，这样就能修当前的课程了。

也就是说，需要一个数据结构支持加入数据，以及删除最大的数据，毫无疑问这个就是优先队列。

所以做法就出来了：

  • 按照截止时间排序
  • 遍历每门课程
  • 修当前课程，并将当前课程的持续时间加入优先队列
  • 如果修完之后的时间大于截止时间，反悔，从优先队列删除掉一门持续时间最大的课程，并累减当前时间
  • 最后的结果就是优先队列的大小

代码如下：

cpp 复制代码 
class Solution {
public:
    int scheduleCourse(vector<vector<int> > &courses) {
        // 按照截止时间排序
        ranges::sort(courses, [](const auto &a, const auto &b) {
            return a[1] < b[1];
        });
        // 当前时间，尽管题目说明从1开始，取0方便计算
        int cur = 0;
        // 优先队列，存储持续时间
        priority_queue<int> q;
        // 遍历
        for (auto &c: courses) {
            // 修当前课程
            cur += c[0];
            // 加入持续时间到优先队列中
            q.push(c[0]);
            // 如果当前时间超出了截止时间
            if (cur > c[1]) {
                // 反悔，不修之前的持续时间最长的一门课程
                cur -= q.top();
                // 出队
                q.pop();
            }
        }
        // 优先队列的长度就是结果
        return static_cast<int>(q.size());
    }
};

4.3 Java版本

java 复制代码 
import java.util.*;

public class Solution {
    public int scheduleCourse(int[][] courses) {
        int cur = 0;
        Arrays.sort(courses, Comparator.comparingInt(a -> a[1]));
        PriorityQueue<Integer> q = new PriorityQueue<>(Comparator.reverseOrder());
        for (int[] c : courses) {
            cur += c[0];
            q.add(c[0]);
            if (cur > c[1]) {
                cur -= q.poll();
            }
        }
        return q.size();
    }
}

4.4 Go版本

go 复制代码 
type PriorityQueue []int

func (pq PriorityQueue) Len() int {
	return len(pq)
}
func (pq PriorityQueue) Less(i, j int) bool {
	return pq[i] > pq[j]
}
func (pq PriorityQueue) Swap(i, j int) {
	pq[i], pq[j] = pq[j], pq[i]
}

func (pq *PriorityQueue) Push(x interface{}) {
	*pq = append(*pq, x.(int))
}

func (pq *PriorityQueue) Pop() interface{} {
	old := *pq
	n := len(old)
	item := old[n-1]
	*pq = old[0 : n-1]
	return item
}

func scheduleCourse(courses [][]int) int {
	slices.SortFunc(courses, func(a, b []int) int {
		if a[1] < b[1] {
			return -1
		}
		if a[1] > b[1] {
			return 1
		}
		return 0
	})
	cur := 0
	pq := &PriorityQueue{}
	heap.Init(pq)
	for _, c := range courses {
		cur += c[0]
		heap.Push(pq, c[0])
		if cur > c[1] {
			cur -= heap.Pop(pq).(int)
		}
	}
	return pq.Len()
}

5 课程表4

5.1 原题

5.2 思路

课程表4和之前几个题目有很大不同，求的是先决条件。

由于题目是给出多个查询条件，并且一个课程有多个先决条件，所以需要一种方法存储课程的所有先决条件，然后查询的时候直接取出结果即可。

在本题中，先决条件本质上是一个布尔值，如果使用二维布尔数组存储的话，2是1的先决条件可以简单表示成：

cpp 复制代码 
parent[1][2] = true;

所以，只需要一个二维数组存储一个课程的所有先决条件即可。

但是这里有一个问题就是先决条件之间怎么转移，例如知道课程2的先决条件有[3,5,6,7,8]，修完课程2之后可以修课程9，那么转移的时候就要遍历所有课程2的先决条件并添加到课程9上。另一方面，课程9的先决条件也不一定只有课程2，可能还有课程10、课程11等，这意味着计算等时候需要把课程9的所有先决条件的先决条件都加到课程9的先决条件中，每一个都需要遍历，这样复杂度非常高。

因此，需要对复杂度进行压缩，由于只需要一个布尔值就能表示，这就是bitset的天然使用场景。每个课程的所有先决条件可以简单地使用bitset<100>去存储（由于n的范围[2,100]），并且转移的时候可以非常简单地通过按位或运算处理，速度非常快。

cpp 复制代码 
vector parent(n, bitset<100>());
// 遍历各个邻居，front是队头
for (const int v: graph[front]) {
    // 添加先决条件，将所有front的先决条件（包括front）添加到v的先决条件中
    parent[v] |= parent[front];
}

另一方面先决条件有多个，这里需要使用拓扑排序的方式去处理，先处理完当前课程的先决条件再处理下一个课程的。

代码如下：

cpp 复制代码 
class Solution {
public:
    vector<bool> checkIfPrerequisite(int n, vector<vector<int> > &prerequisites,
                                     vector<vector<int> > &queries) {
        // 入度
        vector in_degree(n, 0);
        // 存储先决条件，这里用bitset<>数组，parent[i].test(j)表示i的先决条件包含j
        // 将一个课程的所有parent压缩在一个bitset内存储，方便后续计算
        vector parent(n, bitset<100>());
        // 存储图
        vector graph(n, vector<int>());
        for (auto &p: prerequisites) {
            // 入度+1
            ++in_degree[p[1]];
            // 表示p[1]的先决条件包含p[0]
            parent[p[1]].set(p[0]);
            // 存储图
            graph[p[0]].push_back(p[1]);
        }
        queue<int> q;
        for (int i = 0; i < n; ++i) {
            // 入度为0，入队
            if (in_degree[i] == 0) {
                q.push(i);
            }
        }
        // 一直遍历直到队列为空
        while (!q.empty()) {
            const int q_size = static_cast<int>(q.size());
            for (int i = 0; i < q_size; ++i) {
                // 队头
                const int front = q.front();
                // 出队
                q.pop();
                // 遍历各个邻居
                for (const int v: graph[front]) {
                    // 添加先决条件，将所有front的先决条件（包括front）添加到v的先决条件中
                    parent[v] |= parent[front];
                    // 入度减1
                    --in_degree[v];
                    // 入队
                    if (in_degree[v] == 0) {
                        q.push(v);
                    }
                }
            }
        }
        vector<bool> res;
        res.reserve(queries.size());
        // 处理结果，如果query[1].test(query[0])为true，表示是先决条件
        for (const auto &query: queries) {
            res.push_back(parent[query[1]].test(query[0]));
        }
        return res;
    }
};

5.3 Java版本

java 复制代码 
import java.util.*;

public class Solution {
    public List<Boolean> checkIfPrerequisite(int numCourses, int[][] prerequisites, int[][] queries) {
        List<Boolean> res = new ArrayList<>();
        int[] inDegree = new int[numCourses];
        List<BitSet> parent = new ArrayList<>();
        List<List<Integer>> graph = new ArrayList<>();
        for (int i = 0; i < numCourses; i++) {
            parent.add(new BitSet(100));
            graph.add(new ArrayList<>());
        }
        for (int[] p : prerequisites) {
            ++inDegree[p[1]];
            parent.get(p[1]).set(p[0]);
            graph.get(p[0]).add(p[1]);
        }
        LinkedList<Integer> q = new LinkedList<>();
        for (int i = 0; i < numCourses; i++) {
            if (inDegree[i] == 0) {
                q.addLast(i);
            }
        }
        while (!q.isEmpty()) {
            int size = q.size();
            for (int i = 0; i < size; i++) {
                int front = q.pollFirst();
                for (int v : graph.get(front)) {
                    parent.get(v).or(parent.get(front));
                    --inDegree[v];
                    if (inDegree[v] == 0) {
                        q.addLast(v);
                    }
                }
            }
        }
        for (int[] query : queries) {
            res.add(parent.get(query[1]).get(query[0]));
        }
        return res;
    }
}

5.4 Go版本

由于Go没有内置的bitset，并且这里的应用场景较为简单，手动实现一个简单的bitset。

由于长度最大只有100，所以实现逻辑是使用两个int64。

这里还有一个注意的点就是，理论上来说需要使用int64(1) << p[0]去代替1 << p[0]，由于LC上的int是int64，所以可以使用1<<p[0]，而不需要使用int64(1) << p[0]。

go 复制代码 
func checkIfPrerequisite(numCourses int, prerequisites [][]int, queries [][]int) []bool {
	inDegree, parent, graph, q, res := make([]int, numCourses), make([][]int64, numCourses),
		make([][]int, numCourses), make([]int, 0), make([]bool, len(queries))
	for i := range parent {
		parent[i] = []int64{0, 0}
	}
	for _, p := range prerequisites {
		inDegree[p[1]]++
		graph[p[0]] = append(graph[p[0]], p[1])
		if p[0] < 64 {
			parent[p[1]][0] |= 1 << p[0]
		} else {
			parent[p[1]][1] |= 1 << (p[0] - 64)
		}
	}
	for i, v := range inDegree {
		if v == 0 {
			q = append(q, i)
		}
	}
	for len(q) > 0 {
		qLen := len(q)
		for i := 0; i < qLen; i++ {
			front := q[0]
			q = q[1:]
			for _, v := range graph[front] {
				parent[v][0] |= parent[front][0]
				parent[v][1] |= parent[front][1]
				inDegree[v]--
				if inDegree[v] == 0 {
					q = append(q, v)
				}
			}
		}
	}
	for i, query := range queries {
		if query[0] < 64 {
			if parent[query[1]][0]&(1<<query[0]) != 0 {
				res[i] = true
			}
		} else {
			if parent[query[1]][1]&(1<<(query[0]-64)) != 0 {
				res[i] = true
			}
		}
	}
	return res
}

6 总结

本文主要介绍了拓扑排序以及三色标记法的实现，在课程表1、2、4都有用到。另外的课程表3是属于反悔贪心，这类题目比较特殊，并不多。

附录放上所有题目的链接。

7 附录

相关推荐
代码or搬砖17 小时前
JVM垃圾回收器
java·jvm·算法
老鼠只爱大米17 小时前
LeetCode算法题详解 15：三数之和
算法·leetcode·双指针·三数之和·分治法·three sum
客卿12317 小时前
C语言刷题--合并有序数组
java·c语言·算法
Qhumaing17 小时前
C++学习：【PTA】数据结构 7-1 实验6-1（图-邻接矩阵）
c++·学习·算法
菜鸟233号17 小时前
力扣416 分割等和子串 java实现
java·数据结构·算法·leetcode
Swift社区17 小时前
LeetCode 469 凸多边形
算法·leetcode·职场和发展
chilavert31817 小时前
技术演进中的开发沉思-298 计算机原理：算法的本质
算法·计算机原理
圣保罗的大教堂17 小时前
leetcode 1458. 两个子序列的最大点积 困难
leetcode
Dream it possible！17 小时前
LeetCode 面试经典 150_二分查找_搜索二维矩阵（112_74_C++_中等）
leetcode·面试·矩阵
热门推荐
01GitHub 镜像站点02安娜的档案(Anna’s Archive) 镜像网站/国内最新可访问入口（持续更新）03Linux下V2Ray安装配置指南04Labelme从安装到标注：零基础完整指南05jdk21下载、安装（Windows、Linux、macOS）06【踩坑笔记】50系显卡适配的 PyTorch 安装07手把手教你通过Gemini3 pro 学生认证，白用一年，手慢无！08Opencode CLI 安装成功,但是启动失败09GitLab 零基础入门指南：从安装到项目管理全流程10Claude Code Plan 模式完全指南：从入门到精通