2015年伊朗数学奥林匹克国家队选拔赛几何

在 △ABC\triangle ABC△ABC 中, H1H_1H1 是 AAA 在 BCBCBC 边的投影, H1H_1H1 与 HHH 关于 BCBCBC 边的中点 MMM 对称, 分别过点 BBB 和点 CCC 的 (ABC)(ABC)(ABC) 的切线交于点 DDD, 过 H1H_1H1 作 DH1DH_1DH1 的垂线, 交直线 ABABAB 于点 FFF, 交直线 ACACAC 于点 GGG. 求证: ∠BDF=∠CDG\angle BDF=\angle CDG∠BDF=∠CDG. (2015, 伊朗数学奥林匹克国家队选拔赛)

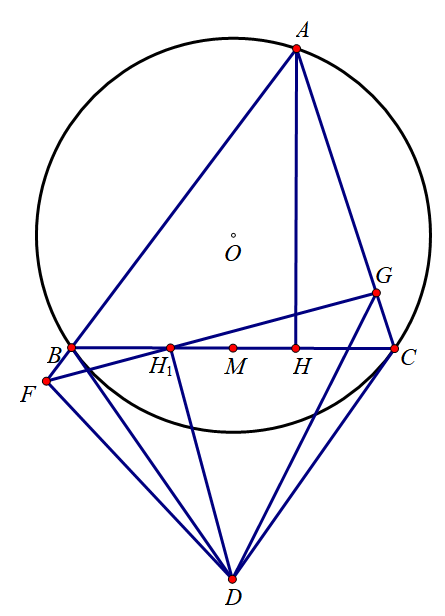
证明:

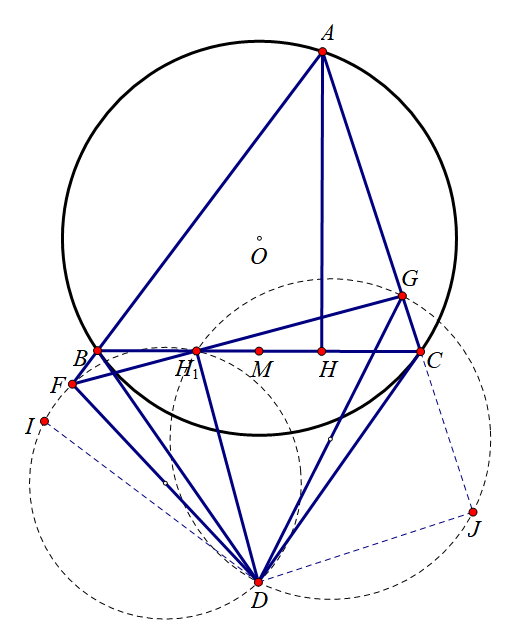
设 DDD 到 ABABAB 和 ACACAC 的投影为 III, JJJ. 显然 FFF, III, DDD, H1H_1H1 共圆, GGG, JJJ, DDD, H1H_1H1 共圆.

BF/BD=sin⁡∠BDFsin⁡∠IFDBF/BD=\frac{\sin \angle BDF}{\sin \angle IFD}BF/BD=sin∠IFDsin∠BDF.

CG/CD=sin⁡∠CDGsin⁡∠JGDCG/CD=\frac{\sin \angle CDG}{\sin \angle JGD}CG/CD=sin∠JGDsin∠CDG.

BF/CG=sin⁡∠BDFsin⁡∠CDGsin⁡∠JGDsin⁡∠IFDBF/CG=\frac{\sin \angle BDF}{\sin \angle CDG}\frac{\sin \angle JGD}{\sin \angle IFD}BF/CG=sin∠CDGsin∠BDFsin∠IFDsin∠JGD.

只需证明: BF/CG=sin⁡∠JGDsin⁡∠IFD=JDGDFDIDBF/CG=\frac{\sin \angle JGD}{\sin \angle IFD}=\frac{JD}{GD}\frac{FD}{ID}BF/CG=sin∠IFDsin∠JGD=GDJDIDFD.

由梅涅劳斯定理, BF/CG=ABACFH1GH1BF/CG=\frac{AB}{AC} \frac {FH_1}{GH_1}BF/CG=ACABGH1FH1.

只需证明: ABACIDJDFH1FDGDGH1=1\frac{AB}{AC} \frac{ID}{JD} \frac{FH_1}{FD} \frac{GD}{GH_1} = 1ACABJDIDFDFH1GH1GD=1.

结合共圆可知其中 FH1FDGDGH1=sin⁡∠FIH1sin⁡∠GJH1\frac{FH_1}{FD} \frac{GD}{GH_1}=\frac{\sin \angle FIH_1}{\sin \angle GJH_1}FDFH1GH1GD=sin∠GJH1sin∠FIH1.

ABAC=sin⁡∠ACBsin⁡∠ABC\frac{AB}{AC} =\frac{\sin \angle ACB}{\sin \angle ABC}ACAB=sin∠ABCsin∠ACB.

ABACFH1FDGDGH1=sin⁡∠FIH1sin⁡∠ABC/sin⁡∠GJH1sin⁡∠ACB=BH1IH1/CH1JH1=CHBHJH1IH1=bcos⁡Cccos⁡BJH1IH1\frac{AB}{AC} \frac{FH_1}{FD} \frac{GD}{GH_1} = \frac{\sin \angle FIH_1}{\sin \angle ABC} / \frac{\sin \angle GJH_1}{\sin \angle ACB} = \frac{BH_1}{IH_1} / \frac{CH_1}{JH_1} = \frac{CH}{BH} \frac{JH_1}{IH_1} = \frac{b \cos C}{c \cos B} \frac{JH_1}{IH_1}ACABFDFH1GH1GD=sin∠ABCsin∠FIH1/sin∠ACBsin∠GJH1=IH1BH1/JH1CH1=BHCHIH1JH1=ccosBbcosCIH1JH1.

BD=CDBD=CDBD=CD, ∠IBD=C\angle IBD=C∠IBD=C, ∠JCD=B\angle JCD=B∠JCD=B, 所以 IDJD=c/b\frac{ID}{JD} = c/bJDID=c/b.

所以只需证明: JH1IH1=cos⁡Bcos⁡C\frac{JH_1}{IH_1} = \frac{\cos B}{\cos C}IH1JH1=cosCcosB.

sin⁡∠CAM/sin⁡∠BAM=c/b=ID/JD=sin⁡∠DJI/sin⁡∠DIJ\sin \angle CAM/\sin \angle BAM=c/b=ID/JD=\sin \angle DJI/\sin \angle DIJsin∠CAM/sin∠BAM=c/b=ID/JD=sin∠DJI/sin∠DIJ.

∠CAM+∠BAM=∠DJI+∠DIJ\angle CAM + \angle BAM = \angle DJI + \angle DIJ∠CAM+∠BAM=∠DJI+∠DIJ.

所以 ∠CAM=∠DJI\angle CAM = \angle DJI∠CAM=∠DJI, ∠BAM=∠DIJ\angle BAM = \angle DIJ∠BAM=∠DIJ.

进而 MMM 是 △AIJ\triangle AIJ△AIJ 的垂心.

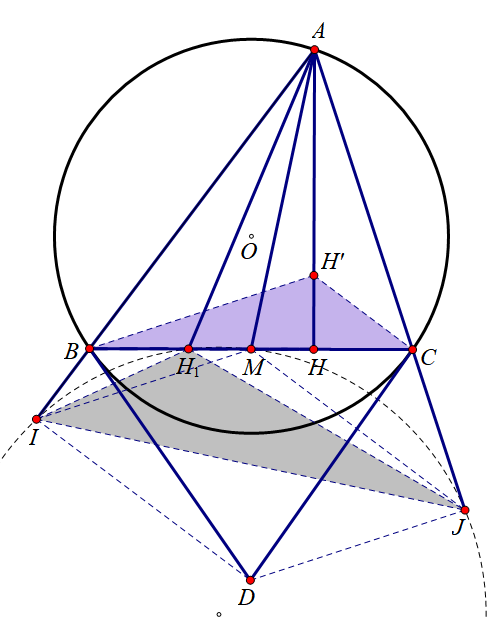
设 △ABC\triangle ABC△ABC 的垂心为 H′H'H′. IM//BH′IM//BH'IM//BH′, JM//CH′JM//CH'JM//CH′.

下面证明: H1H_1H1, MMM, JJJ, III 共圆. 由此可知 JH1IH1=sin⁡∠CMJsin⁡∠BMI=sin⁡∠H′CBsin⁡∠H′BC=BH′CH′=cos⁡Bcos⁡C\frac{JH_1}{IH_1} = \frac{\sin \angle CMJ}{\sin \angle BMI}= \frac{\sin \angle H'CB}{\sin \angle H'BC} = \frac{BH'}{CH'}= \frac{\cos B}{\cos C}IH1JH1=sin∠BMIsin∠CMJ=sin∠H′BCsin∠H′CB=CH′BH′=cosCcosB.

由三弦定理, 只需证明: H1Msin⁡∠IMJ+MJsin⁡∠H1MI=MIsin⁡∠CMJH_1M \sin\angle IMJ + MJ \sin \angle H_1MI = MI \sin \angle CMJH1Msin∠IMJ+MJsin∠H1MI=MIsin∠CMJ.

H1M=HMH_1M = HMH1M=HM, sin⁡∠IMJ=sin⁡A\sin \angle IMJ= \sin Asin∠IMJ=sinA, sin⁡∠H1MI=cos⁡C\sin \angle H_1MI=\cos Csin∠H1MI=cosC, sin⁡∠CMJ=cos⁡B\sin \angle CMJ=\cos Bsin∠CMJ=cosB.

HMMAsin⁡A=MIMAcos⁡B−MJMAcos⁡C\frac{HM}{MA} \sin A =\frac{MI}{MA}\cos B-\frac{MJ}{MA}\cos CMAHMsinA=MAMIcosB−MAMJcosC.

HMMA=sin⁡∠MAH\frac{HM}{MA} = \sin \angle MAHMAHM=sin∠MAH.

MIMA=sin⁡∠MABcos⁡A\frac{MI}{MA}=\frac{\sin \angle MAB}{\cos A}MAMI=cosAsin∠MAB.

MIMA=sin⁡∠MACcos⁡A\frac{MI}{MA}=\frac{\sin \angle MAC}{\cos A}MAMI=cosAsin∠MAC.

即: sin⁡∠MAHsin⁡∠MACsin⁡Acos⁡A=sin⁡∠MABsin⁡∠MACcos⁡B−cos⁡C\frac{\sin \angle MAH}{\sin \angle MAC}\sin A \cos A = \frac{\sin \angle MAB}{\sin \angle MAC}\cos B-\cos Csin∠MACsin∠MAHsinAcosA=sin∠MACsin∠MABcosB−cosC.

先看左侧:

sin⁡∠MAHsin⁡∠MAC=MHMCACAH=a−2bcos⁡Casin⁡C=sin⁡A−2sin⁡Bcos⁡Csin⁡Asin⁡C=sin⁡(C−B)sin⁡Asin⁡C\frac{\sin \angle MAH}{\sin \angle MAC} = \frac{MH}{MC}\frac{AC}{AH}=\frac{a-2b\cos C}{a \sin C}=\frac{\sin A-2\sin B\cos C}{\sin A \sin C} = \frac{\sin (C-B)}{\sin A\sin C}sin∠MACsin∠MAH=MCMHAHAC=asinCa−2bcosC=sinAsinCsinA−2sinBcosC=sinAsinCsin(C−B).

sin⁡∠MAHsin⁡∠MACsin⁡Acos⁡A=sin⁡(C−B)cos⁡Asin⁡C=sin⁡(2B)−sin⁡(2C)2sin⁡C\frac{\sin \angle MAH}{\sin \angle MAC}\sin A \cos A = \frac{\sin (C-B)\cos A}{\sin C} = \frac{\sin (2B)-\sin (2C)}{2\sin C}sin∠MACsin∠MAHsinAcosA=sinCsin(C−B)cosA=2sinCsin(2B)−sin(2C).

再看右侧:

sin⁡∠MABsin⁡∠MAC=sin⁡Bsin⁡C\frac{\sin \angle MAB}{\sin \angle MAC}=\frac{\sin B}{\sin C}sin∠MACsin∠MAB=sinCsinB.

sin⁡∠MABsin⁡∠MACcos⁡B−cos⁡C=sin⁡Bcos⁡B−sin⁡Ccos⁡Csin⁡C=sin⁡(2B)−sin⁡(2C)2sin⁡C\frac{\sin \angle MAB}{\sin \angle MAC}\cos B-\cos C = \frac{\sin B\cos B-\sin C\cos C}{\sin C}=\frac{\sin (2B)-\sin (2C)}{2\sin C}sin∠MACsin∠MABcosB−cosC=sinCsinBcosB−sinCcosC=2sinCsin(2B)−sin(2C).

左右两侧相等.

所以 H1H_1H1, MMM, JJJ, III 共圆.

证毕.

完稿: 2026/01/08