机器学习——DBSCAN算法

K-means算法的优点：简单，快速，适合常规的数据集

缺点：k值难以确定，很难发现任意形状的簇

针对K-means算法的缺点，我们来介绍新的DBSCAN算法

DBSCAN 概念

DBSCAN（Density-Based Spatial Clustering of Applications with Noise）

基于密度的带噪声的空间聚类应用算法，它是将簇定义为密度相连的点的最大集合，能够把具有足够高密度的区域划分为簇，并在噪声的空间数据集中发现任意形状的聚类。

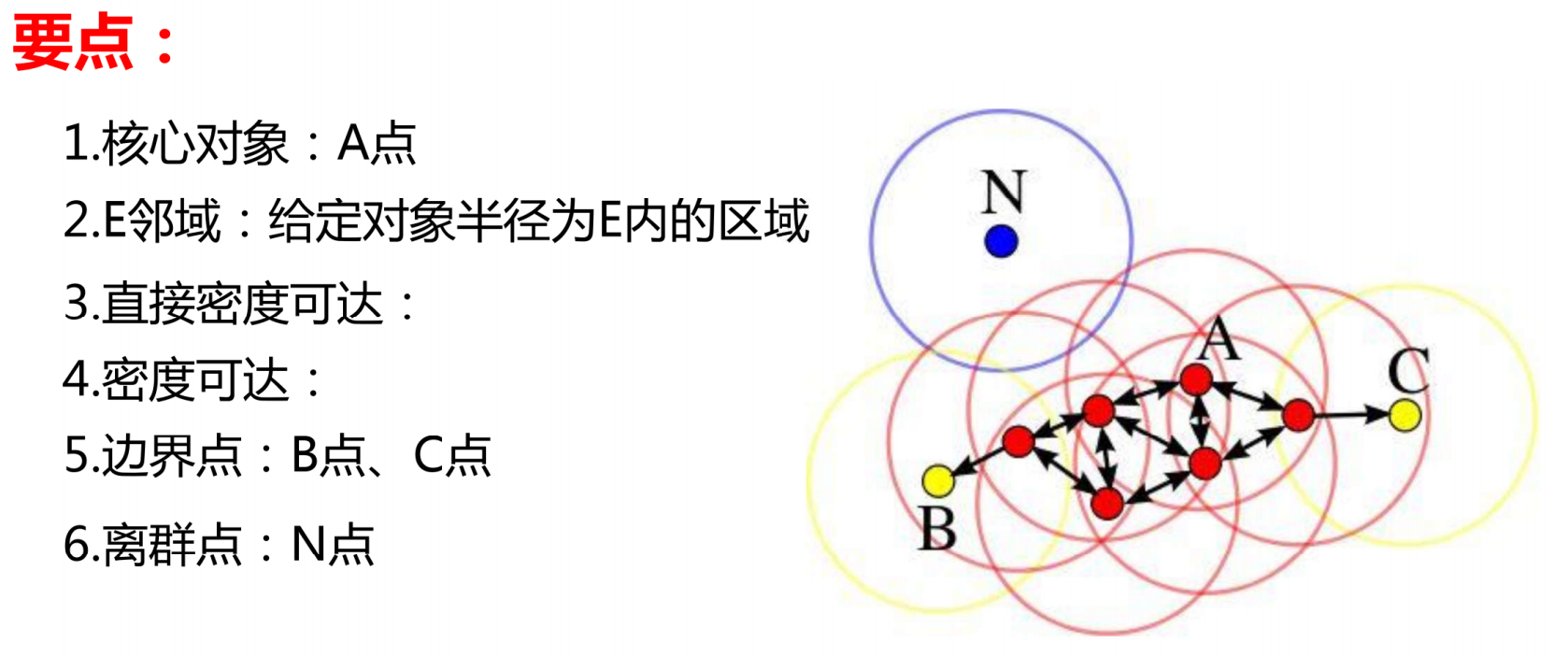
要理解这一算法，首先需要掌握以下六个关键概念：

核心对象（Core Object）：假设存在一个数据点 A，以 A 为中心、指定半径 ε（E 邻域半径）画一个圆，若该圆形区域内包含的数据点数量达到或超过预设的密度阈值 MinPts，则点 A 被称为核心对象。核心对象是聚类形成的基础，代表了密度足够高的区域核心。
E 邻域（Epsilon Neighborhood）：给定数据对象，以该对象为中心、半径为 ε 的圆形区域（在高维空间中为超球体）称为该对象的 E 邻域。E 邻域是衡量数据点密度的重要范围，其半径 ε 的取值直接影响聚类结果的精细程度。
直接密度可达（Directly Density-Reachable）：若数据点 B 位于核心对象 A 的 E 邻域内，则称点 B 从点 A 直接密度可达。这种可达关系是单向的，仅当 A 为核心对象时，B 才能从 A 直接密度可达，反之则不成立。
密度可达（Density-Reachable）：若存在一条数据点链 A₁、A₂、...、Aₙ，其中 A₁为核心对象，A₂从 A₁直接密度可达，A₃从 A₂直接密度可达，...，Aₙ从 Aₙ₋₁直接密度可达，则称点 Aₙ从点 A₁密度可达。密度可达关系具有传递性，是形成聚类簇的关键纽带。
边界点（Border Point）：数据点 B、C 满足以下条件则为边界点：一是它们本身不是核心对象（即其 E 邻域内的数据点数量小于 MinPts）；二是存在核心对象，使得这些点从该核心对象密度可达。边界点属于某一聚类簇，但不具备成为核心对象的密度条件，是聚类簇的边缘部分。
离群点（Outlier/Noise）：数据点 N 既不是核心对象，也无法从任何核心对象密度可达，则称其为离群点。离群点不隶属于任何聚类簇，代表数据集中的噪声或异常值，这也是 DBSCAN 算法 "带噪声" 特性的体现。

可总结为一张图

DBSCAN 算法实现过程

DBSCAN 算法的实现逻辑清晰，主要分为四个核心步骤，无需迭代计算，效率较高：

（一）输入参数与数据集

首先需要明确算法的输入内容：一是待聚类的原始数据集，数据集可以是二维、三维甚至高维空间中的数据点集合；二是两个关键参数，即 E 邻域半径 ε 和密度阈值 MinPts。这两个参数的选择是 DBSCAN 算法应用的核心，后续会详细介绍参数选择的方法。

（二）遍历数据点，识别核心对象

遍历数据集中的每一个数据点，对于每个点，计算其 E 邻域内包含的其他数据点数量。若该数量大于或等于 MinPts，则将该点标记为核心对象，存入核心对象集合中。这一步骤的核心是筛选出密度足够高的 "种子点"，为后续聚类簇的形成奠定基础。

（三）基于核心对象，扩展聚类簇

从核心对象集合中随机选取一个未被访问的核心对象，以该核心对象为起点，寻找所有从它密度可达的数据点，这些点共同构成一个聚类簇。在扩展过程中，若遇到其他未被访问的核心对象，将其所有密度可达的点也纳入当前聚类簇，直到没有新的数据点可以加入该簇为止。此时，该聚类簇构建完成，标记簇内所有点为已访问。

（四）标记离群点

重复步骤（三），直到所有核心对象都被访问完毕。此时，数据集中未被任何聚类簇包含的点，即为离群点（噪声点），将其单独标记。至此，整个聚类过程结束，最终得到若干个密度相连的聚类簇和一组离群点。

可总结为以下三点

DBSCAN 算法的优缺点

（一）优点

无需指定簇数量：与 K-means 不同，DBSCAN 无需人工预先确定聚类簇的数量，可根据数据的密度分布自动识别簇的个数，降低了参数设置的难度。
支持任意形状簇：这是 DBSCAN 最突出的优势，它不受簇形状的限制，无论是环形、条形还是不规则形状的簇，都能准确识别，适用于处理复杂结构的数据集。
天然识别噪声：算法在聚类过程中可直接标记离群点，无需额外的噪声检测步骤，对含有噪声的数据集具有较强的鲁棒性。
对数据分布无要求：无需假设数据服从某种特定的分布（如正态分布），可处理密度不均匀、分布复杂的数据集。

（二）缺点

参数敏感性高：ε 和 MinPts 的取值对聚类结果影响极大，参数设置不当可能导致聚类效果极差（如簇被拆分或合并，噪声点过多或过少）。
高维数据处理能力有限：在高维空间中，距离的定义变得模糊，E 邻域的密度计算准确性下降，导致聚类效果变差。此时需要结合 PCA 等降维技术预处理数据。
密度不均匀数据集处理困难：当数据集中不同簇的密度差异较大时，统一的 ε 和 MinPts 难以适应所有簇，可能导致密度较低的簇被误判为噪声，或密度较高的簇被拆分。
大规模数据集效率较低：朴素的 DBSCAN 算法时间复杂度为 O (n²)，对于百万级以上的大规模数据集，计算每个点的 E 邻域会消耗大量时间和内存，需通过空间索引（如 KD 树、R 树）优化

DBSCAN的API参数

class sklearn.cluster.DBSCAN (eps=0.5 , min_samples=5 , metric='euclidean' , metric_params=None , algorithm='auto' , leaf_size=30 , p=None , n_jobs=None )

eps ： DBSCAN算法参数，即我们的ϵϵ-邻域的距离阈值，和样本距离超过ϵϵ的样本点不在ϵϵ-邻域内。默认值是0.5.一般需要通过在多组值里面选择一个合适的阈值。eps过大，则更多的点会落在核心对象的ϵϵ-邻域，此时我们的类别数可能会减少，本来不应该是一类的样本也会被划为一类。反之则类别数可能会增大，本来是一类的样本却被划分开。

min_samples： DBSCAN算法参数，即样本点要成为核心对象所需要的ϵϵ-邻域的样本数阈值。默认值是5. 一般需要通过在多组值里面选择一个合适的阈值。通常和eps一起调参。在eps一定的情况下，min_samples过大，则核心对象会过少，此时簇内部分本来是一类的样本可能会被标为噪音点，类别数也会变多。反之min_samples过小的话，则会产生大量的核心对象，可能会导致类别数过少。

metric： 最近邻距离度量参数。可以使用的距离度量较多，一般来说DBSCAN使用默认的欧式距离（即p=2的闵可夫斯基距离）就可以满足我们的需求。可以使用的距离度量参数有：

a) 欧式距离 "euclidean":

b) 曼哈顿距离 "manhattan"

c) 切比雪夫距离"chebyshev"

...

还有一些其他不是实数的距离度量，一般在DBSCAN算法用不上，这里也就不列了。

metric_params ******：******不用管。

******algorithm：******最近邻搜索算法参数，算法一共有三种，第一种是蛮力实现，第二种是KD树实现，第三种是球树实现。对于这个参数，一共有4种可选输入，'brute'对应第一种蛮力实现，'kd_tree'对应第二种KD树实现，'ball_tree'对应第三种的球树实现， 'auto'则会在上面三种算法中做权衡，选择一个拟合最好的最优算法。需要注意的是，如果输入样本特征是稀疏的时候，无论我们选择哪种算法，最后scikit-learn都会去用蛮力实现'brute'。个人的经验，一般情况使用默认的 'auto'就够了。如果数据量很大或者特征也很多，用"auto"建树时间可能会很长，效率不高，建议选择KD树实现'kd_tree'，此时如果发现'kd_tree'速度比较慢或者已经知道样本分布不是很均匀时，可以尝试用'ball_tree'。而如果输入样本是稀疏的，无论你选择哪个算法最后实际运行的都是'brute'。

******p:******最近邻距离度量参数。只用于闵可夫斯基距离和带权重闵可夫斯基距离中p值的选择，p=1为曼哈顿距离， p=2为欧式距离。如果使用默认的欧式距离不需要管这个参数。

【属性】

Labels_:

每个点的分类标签。