
🎬 个人主页 :艾莉丝努力练剑
❄专栏传送门 :《C语言》《数据结构与算法》《C/C++干货分享&学习过程记录》
《Linux操作系统编程详解》《笔试/面试常见算法:从基础到进阶》《Python干货分享》
⭐️为天地立心,为生民立命,为往圣继绝学,为万世开太平
🎬 艾莉丝的简介:

🎬艾莉丝的算法专栏简介:

文章目录
- 常见位运算总结
-
- [1 ~> 刷前必刷题单](#1 ~> 刷前必刷题单)
- [2 ~> 博主手记](#2 ~> 博主手记)
- [033 判断字符是否唯一](#033 判断字符是否唯一)
-
- [1.1 解法(位图的思想):](#1.1 解法(位图的思想):)
- [1.2 算法实现](#1.2 算法实现)
- [1.3 博主手记](#1.3 博主手记)
- [034 丢失的数字](#034 丢失的数字)
-
- [2.1 解法:位运算](#2.1 解法:位运算)
- [2.2 算法实现](#2.2 算法实现)
- [2.3 博主手记](#2.3 博主手记)
- [035 两整数之和](#035 两整数之和)
-
- [3.1 位运算解法的算法思路](#3.1 位运算解法的算法思路)
- [3.2 算法实现](#3.2 算法实现)
- [3.3 博主手记](#3.3 博主手记)
- [036 只出现一次的数字 II](#036 只出现一次的数字 II)
-
- [4.1 解法思路:比特位计数](#4.1 解法思路:比特位计数)
- [4.2 算法实现](#4.2 算法实现)
- [4.3 博主手记](#4.3 博主手记)
- [037 消失的两个数字](#037 消失的两个数字)
-
- [5.1 解法:位运算](#5.1 解法:位运算)
- [5.2 算法实现](#5.2 算法实现)
- [5.3 博主手记](#5.3 博主手记)
- 结尾

常见位运算总结
1 ~> 刷前必刷题单
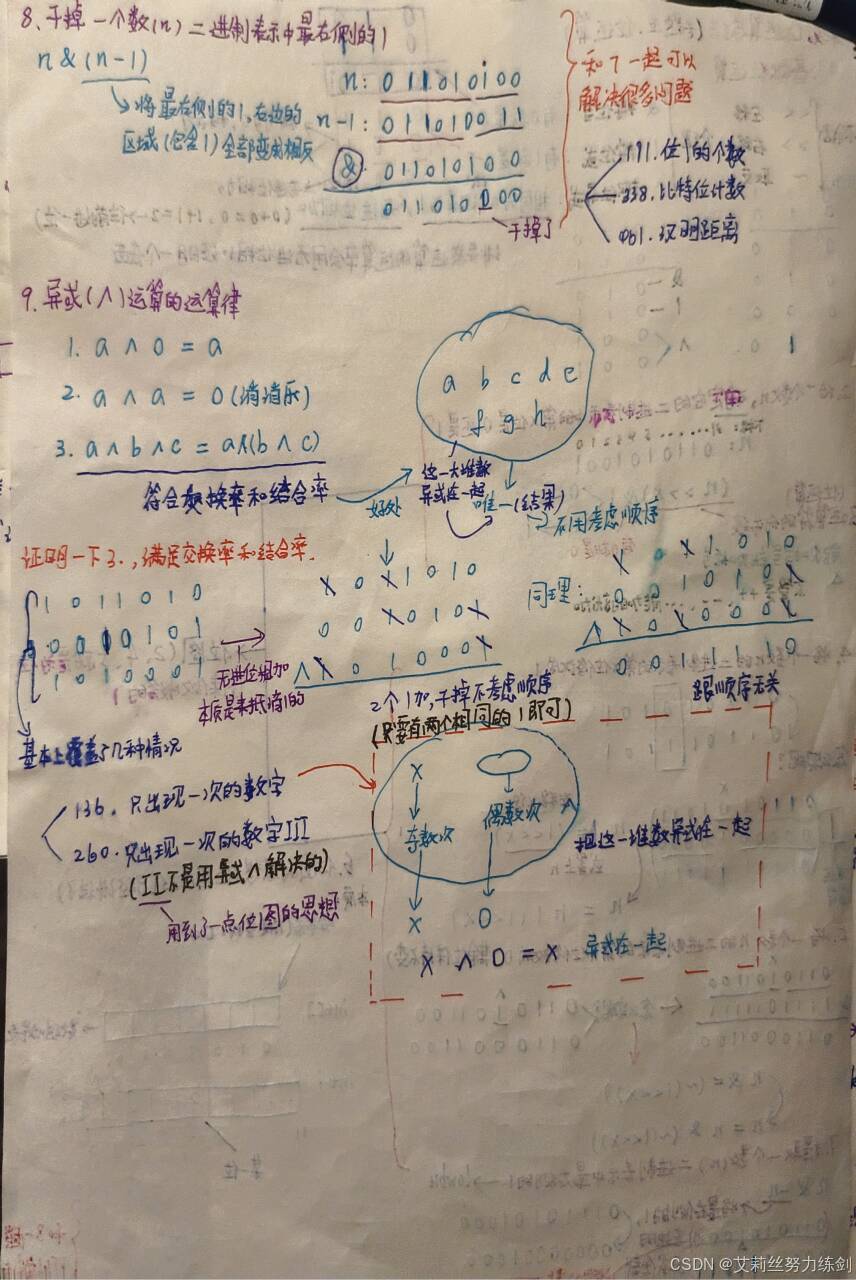
干掉一个数(n)二进制表示中最右侧的1:
cpp
class Solution {
public:
int hammingWeight(int n) {
int count = 0;
while(n)
{
n &= (n - 1);
count++;
}
return count;
}
};
cpp
// 奇偶性动态规划
// class Solution {
// public:
// vector<int> countBits(int n) {
// vector<int> ans(n + 1,0);
// for(int i = 1;i < n + 1;i++)
// {
// ans[i] = ans[i >> 1] + (i & 1);
// }
// return ans;
// }
// };
// 汉明重量问题解法
class Solution {
public:
vector<int> countBits(int n) {
vector<int> ans(n + 1);
for(int i = 1;i < n + 1;i++)
{
int count = 0;
int nums = i;
while(nums)
{
nums &= (nums - 1);
count++;
}
ans[i] = count;
}
return ans;
}
};
cpp
// 干掉一个数二进制位中表示最右侧的1
class Solution
{
public:
int hammingDistance(int x,int y)
{
int val = x ^ y;
int count = 0;
while(val)
{
val &= (val - 1);
count++;
}
return count;
}
};
异或(^)运算的运算律相关的算法题:
cpp
class Solution {
public:
int singleNumber(vector<int>& nums) {
int result = 0;
int i = 0;
while(i < nums.size())
{
result ^= nums[i];
i++;
}
return result;
}
};
cpp
class Solution {
public:
vector<int> singleNumber(vector<int>& nums) {
vector<int> ans(2,0);
int result = 0;
int i = 0;
while(i < nums.size())
{
result ^= nums[i];
i++;
}
unsigned int val = result & (-(unsigned int)result);
i = 0; // 重置i
while(i < nums.size())
{
if(nums[i] & val)
{
ans[0] ^= nums[i];
}
else
{
ans[1] ^= nums[i];
}
i++;
}
return ans;
}
};2 ~> 博主手记

033 判断字符是否唯一
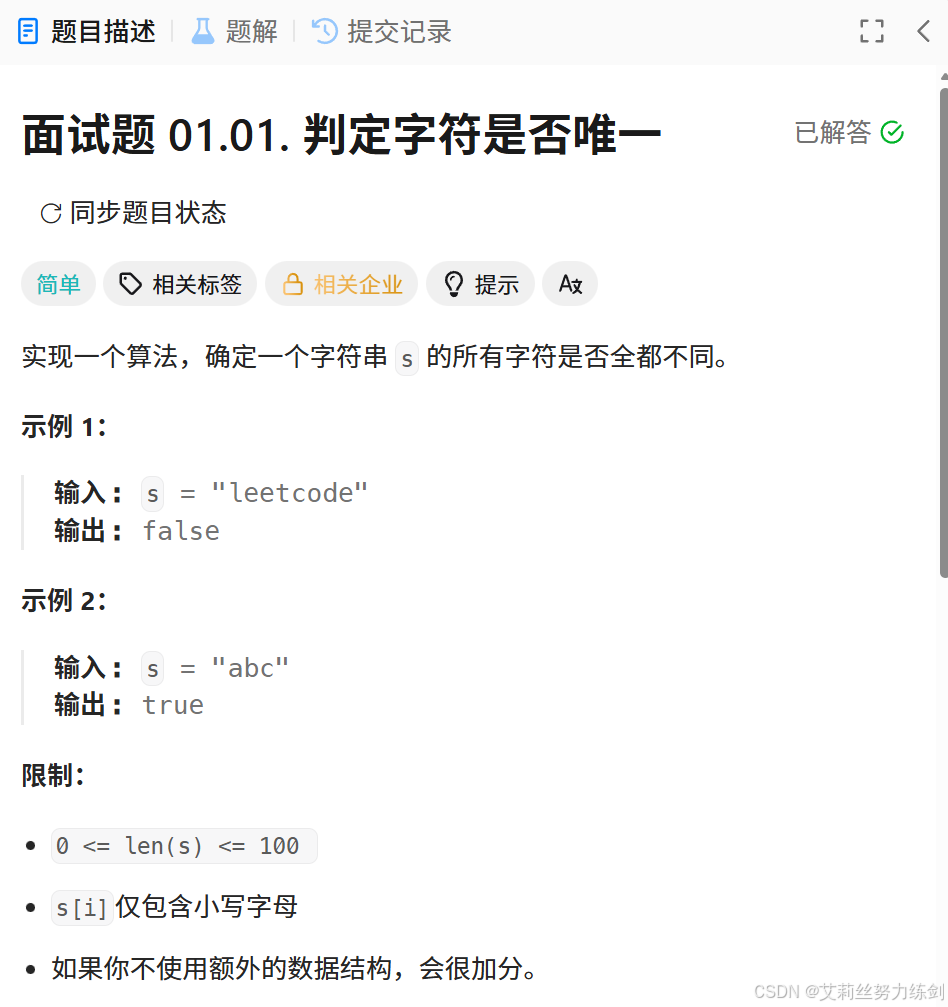
力扣链接: 面试题 01.01. 判定字符是否唯一
题目描述:
1.1 解法(位图的思想):
利用「位图」的思想,每一个【比特位】代表一个【字符】,一个int类型的变量的32位足够表示所有的小写字母。比特位里面如果是0,表示这个字符没有出现过。比特位里面的值是1,表示该字符出现过。
那么我们就可以用一个【整数】来充当【哈希表】。
1.2 算法实现
cpp
class Solution {
public:
bool isUnique(string astr) {
// 利用鸽巢原理做优化
if(astr.size() > 26) return false;
// 搞定位图
int bitMap = 0;
// 遍历字符串
for(auto ch : astr)
{
int i = ch - 'a';
// 先把重复的字符处理一下
if((bitMap >> i) & 1 == 1) return false;
// 说明字符没有出现过,添加到位图中
bitMap |= 1 << i;
}
return true;
}
};
1.3 博主手记
本题整个的思路、算法原理、解题过程博主在纸上推导了一遍,大家可以参考一下手记的推导过程!最好做题的过程中自己也推导一遍!!!自己能够推导很重要!

034 丢失的数字
力扣链接: 268. 丢失的数字
题目描述:

2.1 解法:位运算
设数组的大小为n,那么缺失之前的数就是[0 , n],数组中是在[0,n]中缺失一个数形成的序列。
如果我们把数组中的所有数,以及[0 , n]中的所有数全部【异或】在一起,那么根据【异或】运算的【消消乐】规律,最终的异或结果应该就是缺失的数。
2.2 算法实现
cpp
class Solution {
public:
int missingNumber(vector<int>& nums) {
// 用ret表示确实的那个数字
int ret = 0;
// 把数组中的数异或在一起
for(auto x : nums) ret ^= x;
// 把0~n中的数异或在一起
for(int i = 0;i <= nums.size();i++)
ret ^= i;
return ret;
}
};
2.3 博主手记
本题整个的思路、算法原理、解题过程博主在纸上推导了一遍,大家可以参考一下手记的推导过程!最好做题的过程中自己也推导一遍!!!自己能够推导很重要!

035 两整数之和
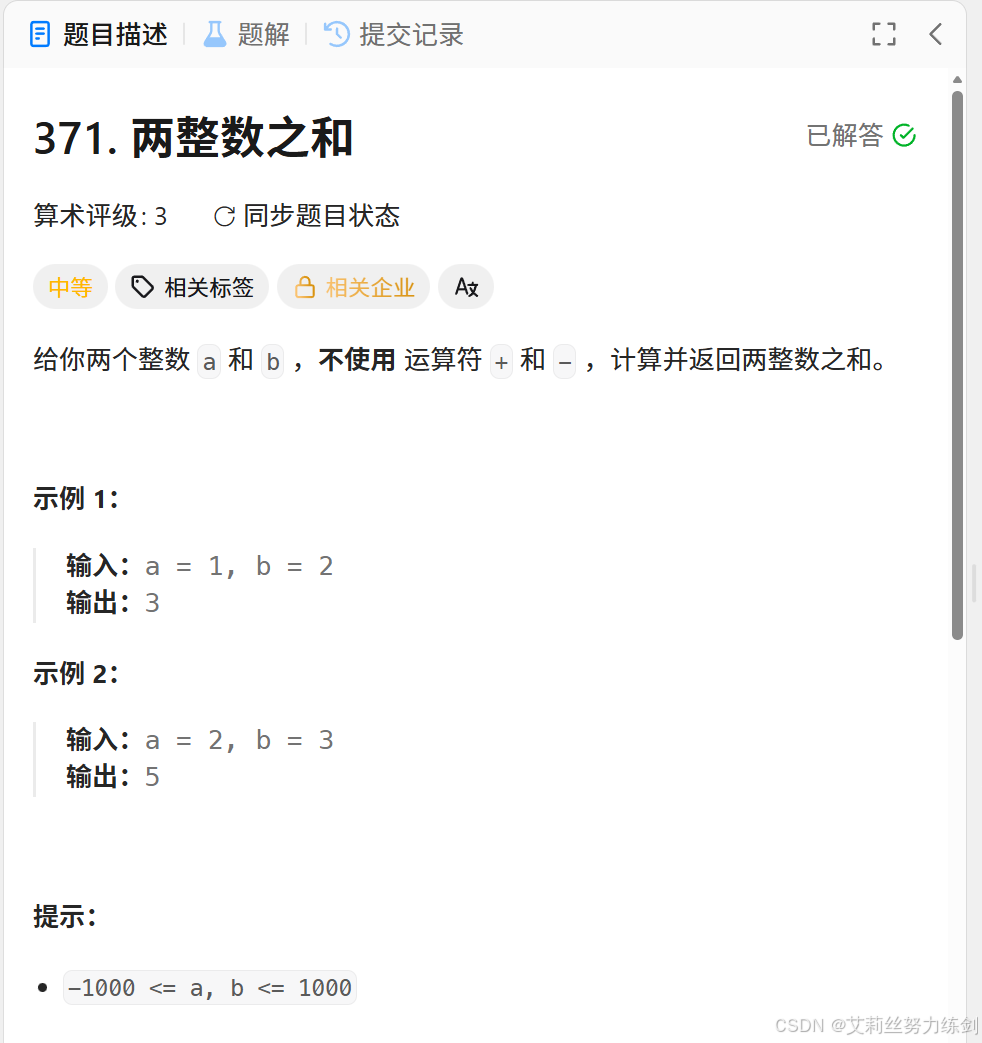
力扣链接: 371. 两整数之和
题目描述:
3.1 位运算解法的算法思路
-
异或
^运算本质是【无进位加法】; -
按位与
&操作能够得到【进位】; -
然后一直循环进行,直到【进位】变成
0为止。
3.2 算法实现
cpp
class Solution {
public:
int getSum(int a, int b) {
while(b != 0) // 一直重复这个操作
{
int x = a ^ b; // 先算出无进位相加的结果
unsigned int carry = (unsigned int)(a & b) << 1; // 算出算出进位
// 这里用unsigned int是考虑到a & b如果是-1的话,此时左移操作是没有定义的,用这种方式处理一下-1的情况(把-1当成无符号的整数)
a = x; // 把无进位相加结果给a
b = carry; // 把进位相加结果给b
}
return a;
}
};
笔试场上可以不讲武德,面试官不看,而且代码也是会通过的:
cpp
class Solution {
public:
int getSum(int a, int b) {
return a + b;
}
};3.3 博主手记
本题整个的思路、算法原理、解题过程博主在纸上推导了一遍,大家可以参考一下手记的推导过程!最好做题的过程中自己也推导一遍!!!自己能够推导很重要!

036 只出现一次的数字 II
力扣链接: 137. 只出现一次的数字 II
题目描述:

4.1 解法思路:比特位计数
设要找的数位ret。
由于整个数组中,需要找的元素只出现了【一次】,其余的数都出现的【三次】,因此我们可以根据所有数的【某一个比特位】的总和%3的结果,快速定位到ret的【一个比特位上】的值是0还是1。
这样,我们通过ret的每一个比特位上的值,就可以将ret给还原出来。
4.2 算法实现
cpp
class Solution {
public:
int singleNumber(vector<int>& nums) {
int ret = 0;
for(int i = 0;i < 32;i++) // 依次去修改 ret 中的每一位
{
int sum = 0;
for(int x : nums) // 计算 nums 中所有的数的第 i 位的和
if(((x >> i) & 1) == 1)
sum++;
sum %= 3;
if(sum == 1) ret |= (1 << i);
}
return ret;
}
};
4.3 博主手记
本题整个的思路、算法原理、解题过程博主在纸上推导了一遍,大家可以参考一下手记的推导过程!最好做题的过程中自己也推导一遍!!!自己能够推导很重要!

037 消失的两个数字
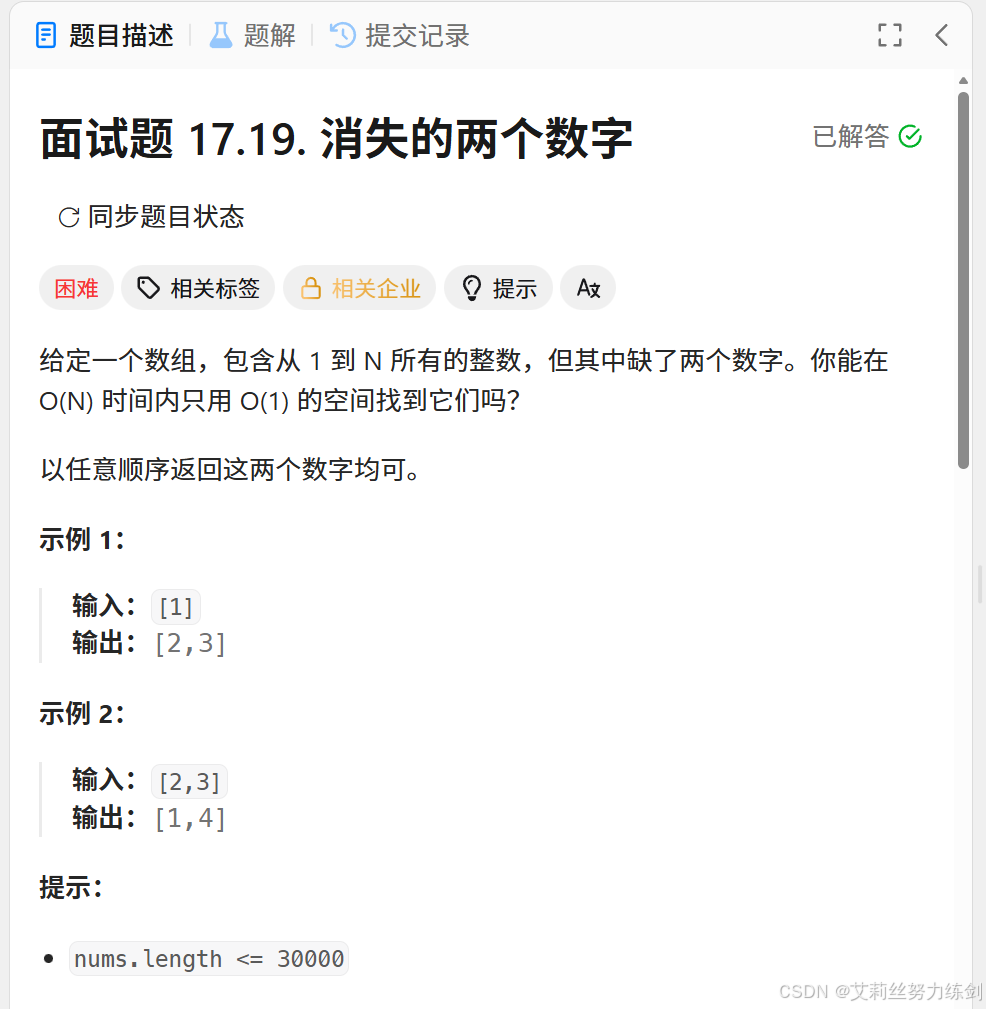
力扣链接: 面试题 17.19. 消失的两个数字
题目描述:
5.1 解法:位运算
本题就是268. 丢失的数字 + 260. 只出现一次的数字 III组合起来的题。
先将数组中的数和[1 , n + 2]区间内的所有数【异或】在一起,问题就变成了:有两个数出现了【一次】,其余所有的数出现了【两次】。进而变成了260. 只出现一次的数字 III这道题。
5.2 算法实现
cpp
class Solution {
public:
vector<int> missingTwo(vector<int>& nums) {
// 1、将所有的数异或在一起
int tmp = 0;
for(auto x : nums) tmp ^= x; // 异或原数组中的数
// 异或1 ~ N
for(int i = 1;i <= nums.size() + 2;i++) tmp ^= i;
// 2、找出a,b中比特位不同的那一位
int diff = 0;
while(1)
{
if(((tmp >> diff) & 1) == 1) break;
else diff++;
}
// 3、根据diff位的不同,将所有的数划分为两类来异或
int a = 0,b = 0;
for(int x : nums)
if(((x >> diff) & 1) == 1) b ^= x;
else a ^= x;
for(int i = 1;i <= nums.size() + 2;i++)
if(((i >> diff) & 1) == 1) b ^= i;
else a ^= i;
return {a,b};
}
};
5.3 博主手记
本题整个的思路、算法原理、解题过程博主在纸上推导了一遍,大家可以参考一下手记的推导过程!最好做题的过程中自己也推导一遍!!!自己能够推导很重要!

结尾
uu们,本文的内容到这里就全部结束了,艾莉丝再次感谢您的阅读!
结语:希望对学习算法相关内容的uu有所帮助,不要忘记给博主"一键四连"哦!
往期回顾:
【优选算法必刷100题】第031~32题(前缀和算法):连续数组、矩阵区域和
🗡博主在这里放了一只小狗,大家看完了摸摸小狗放松一下吧!🗡 ૮₍ ˶ ˊ ᴥ ˋ˶₎ა
