此分类用于记录吴恩达深度学习课程的学习笔记。

课程相关信息链接如下：

原课程视频链接：[双语字幕]吴恩达深度学习deeplearning.ai
github课程资料，含课件与笔记:吴恩达深度学习教学资料
课程配套练习（中英）与答案：吴恩达深度学习课后习题与答案

本篇为第五课的第一周内容，1.10的内容以及一些相关基础的补充。

本周为第五课的第一周内容，与 CV 相对应的，这一课所有内容的中心只有一个：自然语言处理（Natural Language Processing，NLP） 。

应用在深度学习里，它是专门用来进行文本与序列信息建模 的模型和技术，本质上是在全连接网络与统计语言模型基础上的一次"结构化特化"，也是人工智能中最贴近人类思维表达方式 的重要研究方向之一。
这一整节课同样涉及大量需要反复消化的内容，横跨机器学习、概率统计、线性代数以及语言学直觉。

语言不像图像那样"直观可见"，更多是抽象符号与上下文关系的组合，因此理解门槛反而更高 。

因此，我同样会尽量补足必要的背景知识，尽可能用比喻和实例降低理解难度。

本篇的内容关于长短期记忆 LSTM，它和 GRU 一样，是成功缓解 RNN 的长距离依赖问题且流行至今的技术。

1. 什么是 LSTM（Long Short-Term Memory）？

在 GRU 中，我们已经看到：通过门控机制对信息流进行选择性控制，确实可以显著缓解传统 RNN 的长距离依赖问题 。

无论是更新门对历史信息的保留，还是重置门对当前输入的强调，本质上都是在回答同一个问题：哪些信息值得被继续传递，哪些可以被遗忘。

然而，从更长时间跨度的建模需求来看，GRU 仍然存在一个结构上的局限 ：它依然只有单一的隐藏状态 来同时承担"短期计算结果"和"长期记忆载体"这两种角色。

这意味着，即便引入了门控机制，不同时间尺度的信息仍然被迫混合在同一条状态通道中传递，在极长序列或精细时序控制的场景下，这种耦合仍可能限制模型的表达能力。

而LSTM 便能应对这类问题，早在 1997 年，Hochreiter 和 Schmidhuber 在论文：Long Short-Term Memory中，便从理论层面系统性地分析了 RNN 中梯度消失的问题，并给出了一种结构性解决方案 ：通过显式引入一条专门用于长期信息传递的记忆单元（cell state），并配合精细设计的门控结构，使得关键信息可以在长时间跨度内几乎不受干扰地向前传播。

这里要说明一点，你会发现：从时间顺序上看，LSTM 的提出早于 GRU 。

LSTM 是最早从结构层面系统性解决 RNN 长距离依赖问题的门控循环单元。

而在上一篇我们说 GRU 可以看作 LSTM 的一种简化形式，正是因为它在 LSTM 的基础上合并了部分门控结构，取消了显式的记忆单元，用更紧凑的形式实现了相似的建模目标。

也正因为这种简化，GRU 在参数数量、计算开销以及工程实现复杂度上都更为友好。

因此，在许多实际任务中，当序列长度并未极端拉长，或对长期记忆的精细控制要求不高时，GRU 往往能够以更低的成本获得与 LSTM 接近的性能 。这也是为什么，尽管 LSTM 在理论上具备更强的表达与记忆能力，结构更简单的 GRU 仍然在大量 NLP 与时序建模场景中被广泛采用。

同样简单过了过历史，下面我们来展开介绍。

1.1 GRU 的理论局限

在 GRU 中，我们已经看到：通过引入更新门和重置门，模型不再被动地"记住一切"，而是学会了选择性保留与选择性使用历史信息 。

这使得 RNN 在长序列建模中的表现得到了显著改善。

但如果我们继续追问一个问题：这些被"精心筛选"的历史信息，到底被存放在哪里？

答案是：仍然在同一个隐藏状态里。

也就是说，在 GRU 中：隐藏状态既承担当前计算结果 ，又承担长期记忆载体 。

这样做的结果就是我们刚刚提到的：所有信息，无论时间尺度长短，最终都要"挤"在同一个向量中传递，可能限制模型的表达能力。

在多数任务中，这已经足够有效，但在极长序列、精细时序控制或长期语义一致性要求很高 的场景下，这种"混合存储"仍然可能成为瓶颈。

1.2 LSTM 的记忆细胞

实际上，LSTM 的设计就能很好的解决刚刚的混合存储问题。

它引入了一个结构层面的改变 ：不再让同一个状态同时负责"长期记忆"和"短期计算"。

为此，LSTM 明确区分了两条信息通道：

细胞状态（cell state） \(c^{}\) → 专门负责长期信息的存储与传递。
隐藏状态（hidden state） \(a^{}\) → 负责当前时刻的输出与短期计算。

你可以把它理解为：

隐藏状态是"当前脑子里在想什么"，

细胞状态是"一条几乎不被打扰的长期备忘录"。

这也是 LSTM 名字中 Long Short-Term 的含义： 长期信息（Long-Term）和短期信息（Short-Term）在结构上被显式区分了。

打个比方来总结 GRU 和 LSTM 的差别：GRU像是在一张纸上反复修改内容 ，LSTM则像是单独准备了一本笔记本。

1.3 LSTM 的门控机制

既然引入了专门的记忆细胞来作为 LSTM 中的长期记忆通道，新的问题自然出现了：这条记忆，什么时候该保留？什么时候该更新？什么时候该输出给当前计算使用？

答案依然是：门控机制 。

简单来说，LSTM 通过三道门来精细控制长期记忆：

遗忘门（Forget Gate）：决定旧记忆保留多少。
输入门（Input Gate）：决定新信息写入多少。
输出门（Output Gate）：决定当前时刻对外暴露多少记忆。

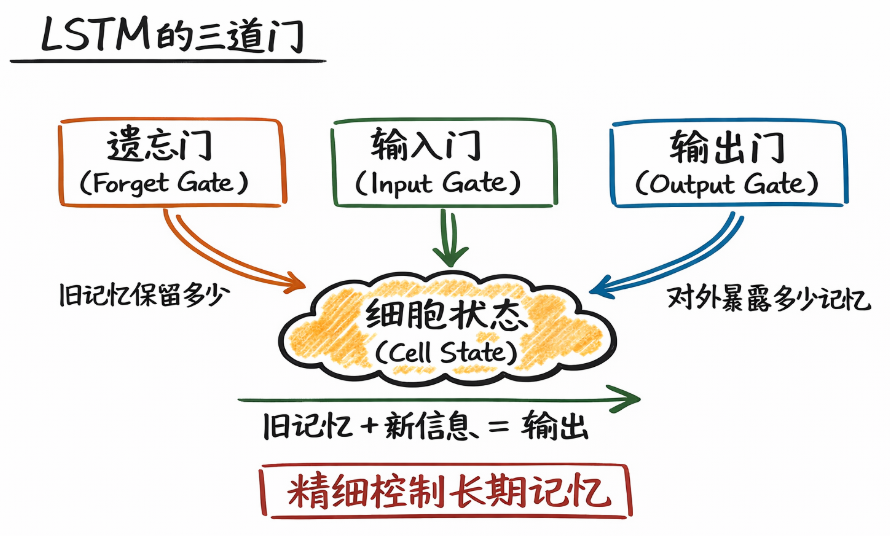
也正是因为这些门的存在， cell state 才能够在时间维度上稳定流动，而不被频繁改写 。

有了 GRU 的基础后，我们就不再单独逐个展开每道门的语义了，在下面的实现部分再来详细展开它们的作用逻辑。

2. 如何实现 LSTM？

在之前的 GRU 中，我们已经看到：门控的本质不是增加复杂度，而是为"信息是否继续存在"提供可学习的选择权。

LSTM 在这个思想上更进一步：它不再试图让同一个状态 同时承担"长期记忆"和"当前计算"，而是显式引入了一条几乎线性传播的长期记忆通道------细胞状态 \(c^{\langle t \rangle}\) ，并通过遗忘门，输入门和输出门来控制细胞状态。

了解了基本原理后，现在就来看看，在一个时间步 \(t\)，一个标准 LSTM 单元是如何实现的。

实际上，它只是比 GRU 多了些步骤，在有了 GRU 的基础后，LSTM 的实现并不难理解，先摆出它的单元结构图如下：

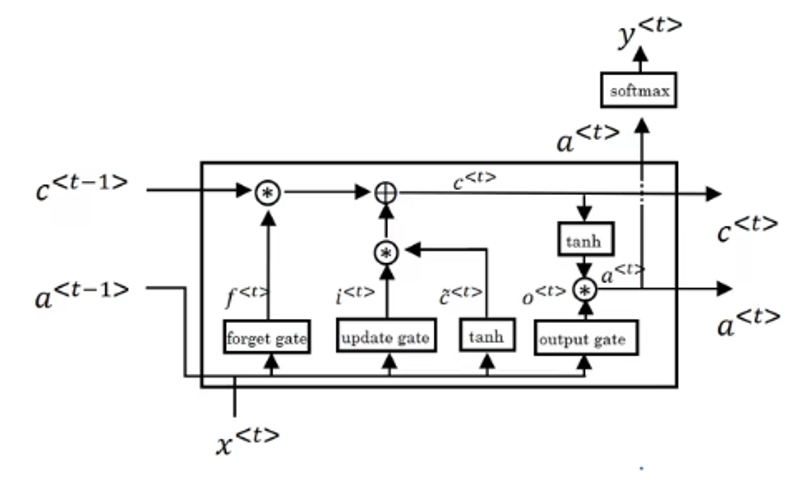
要强调的还是我们介绍的计算顺序是逻辑上的先后顺序，实际上很多步骤都是可以同步计算的。

2.1 计算遗忘门（Forget Gate）

LSTM 的第一步，是计算 遗忘门 \(f^{\langle t \rangle}\)。

它的作用就相当于 GRU 的重置门：对上一时刻的细胞状态 \(c^{\langle t-1 \rangle}\) 进行"按比例保留"。

但要注意，这里是"细胞状态 " 而不是 "隐藏状态 "。

过程如下：

计算公式还是是线性组合：

\[f^{\langle t \rangle} = sigmoid\big( W_{xf} x^{\langle t \rangle} + W_{af} a^{\langle t-1 \rangle} + b_f \big) \]

遗忘门值的含义是这样的：

\(f^{\langle t \rangle}_i \approx 1\)：第 \(i\) 个记忆单元几乎完全保留。
\(f^{\langle t \rangle}_i \approx 0\)：第 \(i\) 个记忆单元被主动遗忘。

这里出现了新的内容需要说明：细胞状态 \(c^{\langle t \rangle}\) 与隐藏状态 \(a^{\langle t \rangle}\) 在维度上是一致的 。

若隐藏状态是一个 \(d\) 维向量，那么细胞状态同样包含 \(d\) 个记忆单元 。

因此，遗忘门 \(f^{\langle t \rangle}\) 的每一个分量 \(f_i^{\langle t \rangle}\)，并不是控制"一整段记忆"，而是独立控制第 \(i\) 个记忆单元在时间维度上的保留比例。

再结合一下 GRU ，你会发现，这段逻辑在GRU中以重置门的形式完整保留了。

2.2 计算输入门（Input Gate）

LSTM 的第二步，是计算 输入门 \(i^{\langle t \rangle}\)。

它的作用是：决定当前步生成的新信息有多少可以写入细胞状态 \(c^{\langle t \rangle}\) 。

换句话说，它控制了"新记忆更新比例"，在功能上类似 GRU 的更新门，但在 LSTM 中，它只负责 新信息写入，而历史信息保留由遗忘门控制。

过程如下：

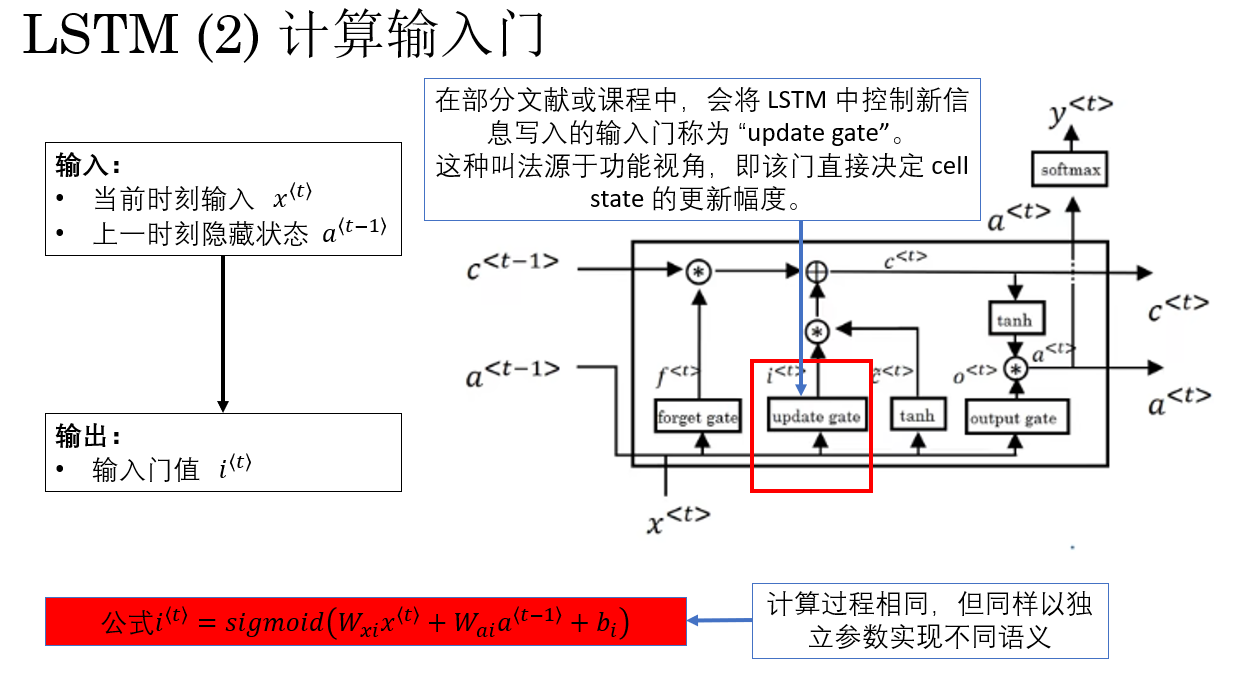
公式表示为：

\[i^{\langle t \rangle} = sigmoid\big( W_{xi} x^{\langle t \rangle} + W_{ai} a^{\langle t-1 \rangle} + b_i \big) \]

输入门值的语义同样清晰：

\(i_i^{\langle t \rangle} \approx 1\)：第 \(i\) 个记忆单元几乎全部接收新信息。
\(i_i^{\langle t \rangle} \approx 0\)：第 \(i\) 个记忆单元几乎不写入新信息。

同样地，输入门 \(i^{\langle t \rangle}\) 与细胞状态 \(c^{\langle t \rangle}\) 的维度一致，每个分量独立控制对应记忆单元的写入比例。

这样做可以保证 长期记忆在时间维度上既保留重要信息，又按需更新新内容，实现更精细的记忆管理。

2.3 计算候选细胞状态（Candidate Cell State）

还是要先强调一点，这是"候选细胞状态 "，不是"候选隐藏状态"。到这一步，隐藏状态还没有出场。

在计算完输入门 \(i^{\langle t \rangle}\) 之后，LSTM 的下一步是生成 候选细胞状态 \(\tilde{c}^{\langle t \rangle}\)。

它的作用是：表示当前步的新信息内容 ，由当前输入 \(x^{\langle t \rangle}\) 和上一时刻隐藏状态 \(a^{\langle t-1 \rangle}\) 共同决定，但尚未写入细胞状态 \(c^{\langle t \rangle}\)。

换句话说，候选细胞状态就是 准备好可以写入的"新记忆" 。

计算过程如下：

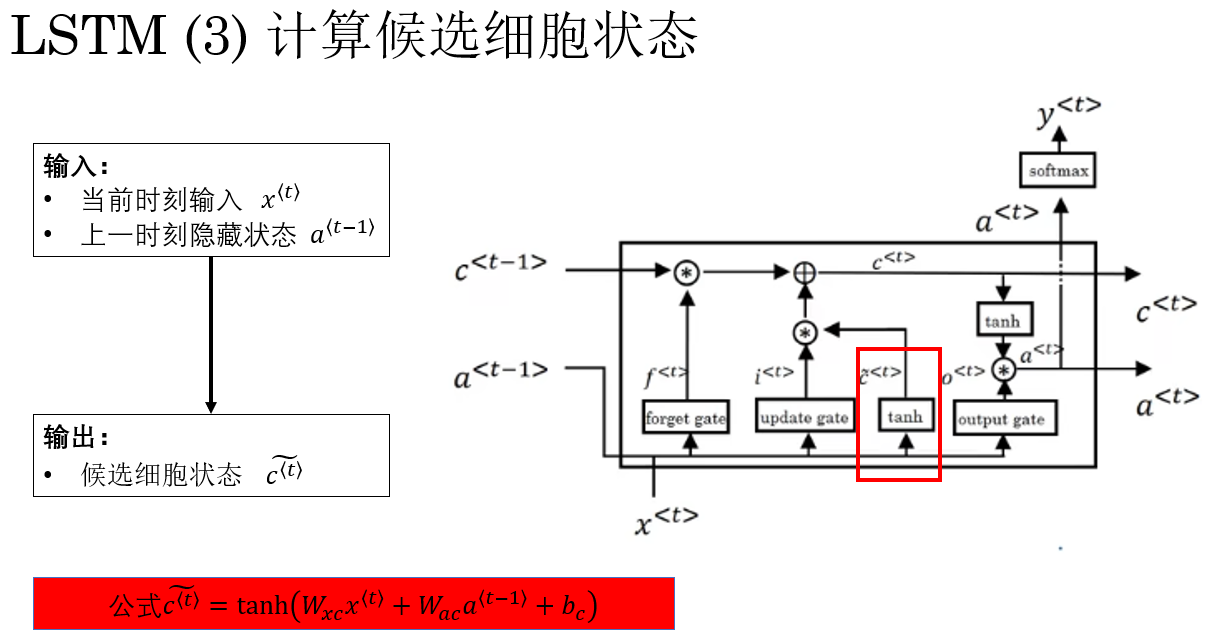
公式表示为：

\[\tilde{c}^{\langle t \rangle} = \tanh\big( W_{xc} x^{\langle t \rangle} + W_{ac} a^{\langle t-1 \rangle} + b_c \big) \]

到后下一步你就会发现：候选状态本身并不直接影响最终输出，它只是表示"有多少新记忆"，而输入门 \(i^{\langle t \rangle}\) 才决定"写入多少新记忆"。

这段设计不同于 GRU：LSTM 将"新信息生成"和"新信息写入"明确分离，方便通过门控精细控制记忆更新。

2.4 更新细胞状态

现在我们已经有了这样东西：

上一时刻的细胞状态 \(c^{\langle t-1 \rangle}\)（旧长期记忆）
遗忘门 \(f^{\langle t \rangle}\)（保留比例）
输入门 \(i^{\langle t \rangle}\) 与候选记忆 \(\tilde{c}^{\langle t \rangle}\)（新信息）
LSTM 会用下面这个核心公式来更新长期记忆：

\[c^{\langle t \rangle} = f^{\langle t \rangle} \odot c^{\langle t-1 \rangle} + i^{\langle t \rangle} \odot \tilde{c}^{\langle t \rangle} \]

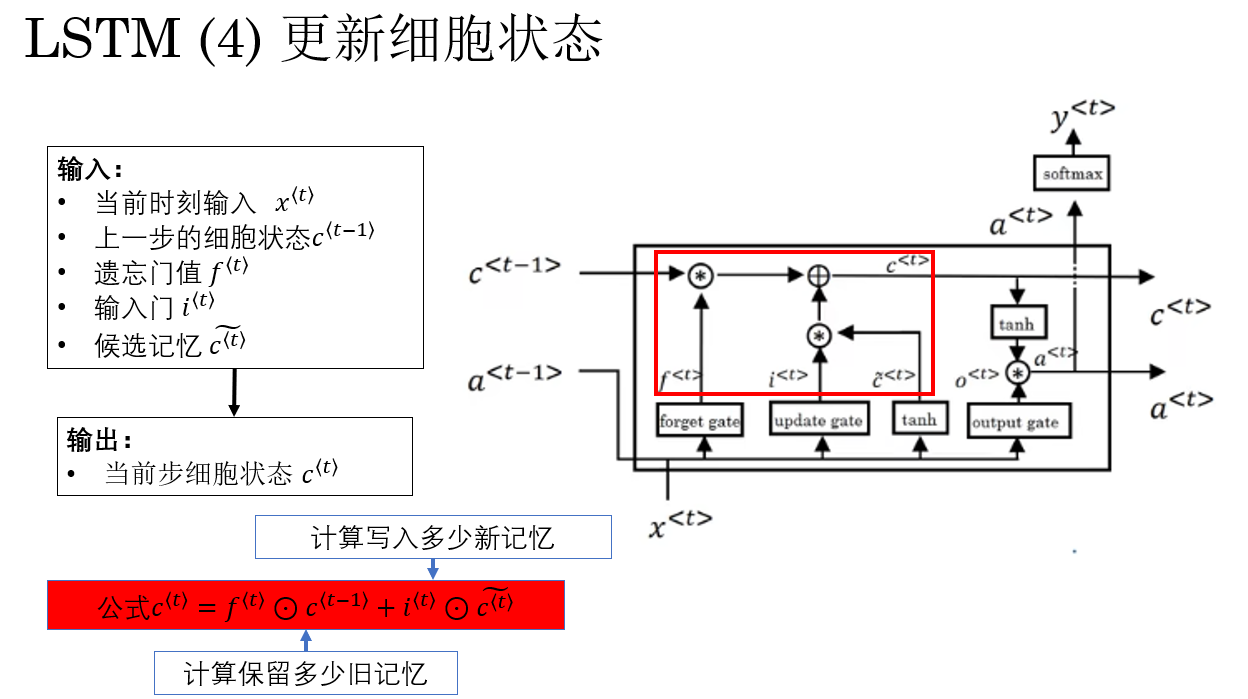
这个公式的意义也非常直观：

第一项：保留多少旧记忆。
第二项：写入多少新记忆 。
也正是因为这里存在一条近似"直通"的路径，让梯度可以直接从 \(c^{\langle t \rangle}\) 回传到 \(c^{\langle t-1 \rangle}\) ， 细胞状态才能在时间维度上稳定传播，梯度也不容易衰减。

3.5 计算输出门（Output Gate）

需要特别强调的是： 细胞状态并不直接作为模型输出。

在之前几步完成了对细胞状态的更新，我们到这里才开始进行与模型输出相关的隐藏状态计算。

在更新完细胞状态 \(c^{\langle t \rangle}\) 之后，LSTM 的下一步是计算 输出门 \(o^{\langle t \rangle}\)

输出门的作用是：控制细胞状态中的信息有多少被"暴露"给下一层或下一时间步使用 。

换句话说，输出门决定了"长期记忆通道中的信息如何影响当前计算"。

计算过程已经看了很多遍了：

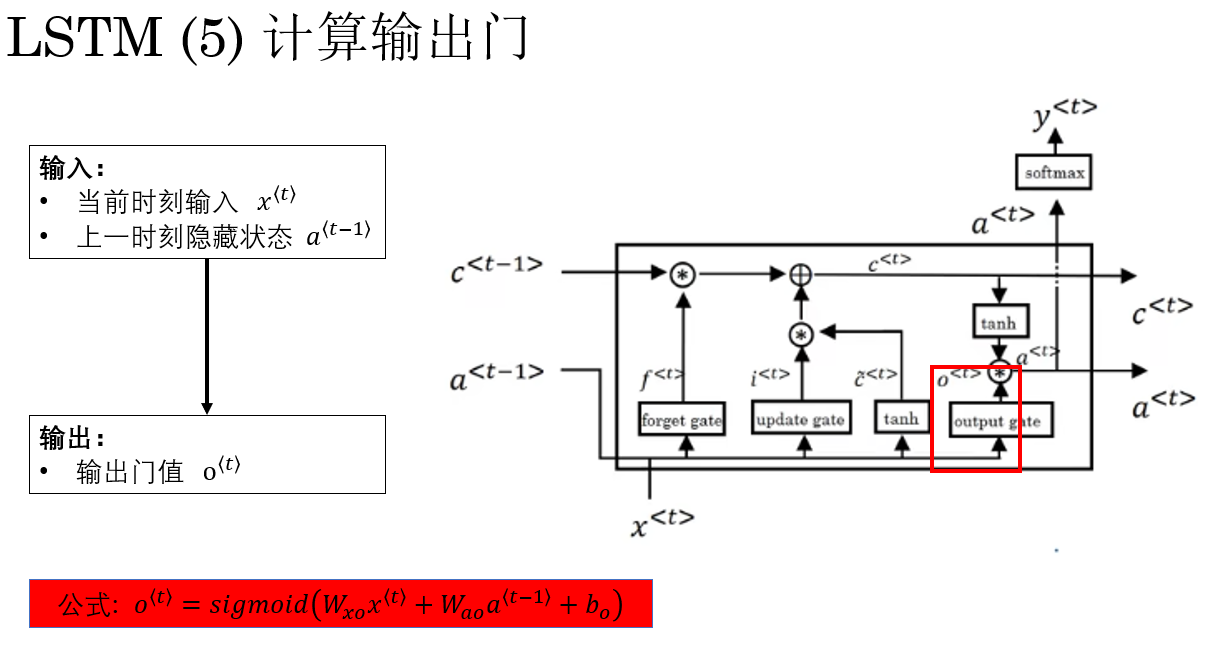
门的计算都是相同的，公式为：

\[o^{\langle t \rangle} = sigmoid\big( W_{xo} x^{\langle t \rangle} + W_{ao} a^{\langle t-1 \rangle} + b_o \big) \]

当 \(o_i^{\langle t \rangle} \approx 1\) 时，第 \(i\) 个记忆单元的长期信息几乎全部暴露给隐藏状态。
当 \(o_i^{\langle t \rangle} \approx 0\) 时，第 \(i\) 个记忆单元的长期信息几乎完全屏蔽。

3.6 更新隐藏状态

有了输出门 \(o^{\langle t \rangle}\) 和更新后的细胞状态 \(c^{\langle t \rangle}\) 后，就可以生成当前时刻的隐藏状态 \(a^{\langle t \rangle}\)，这也是 LSTM 的实际输出，用于传递到下一时间步或下一层网络。

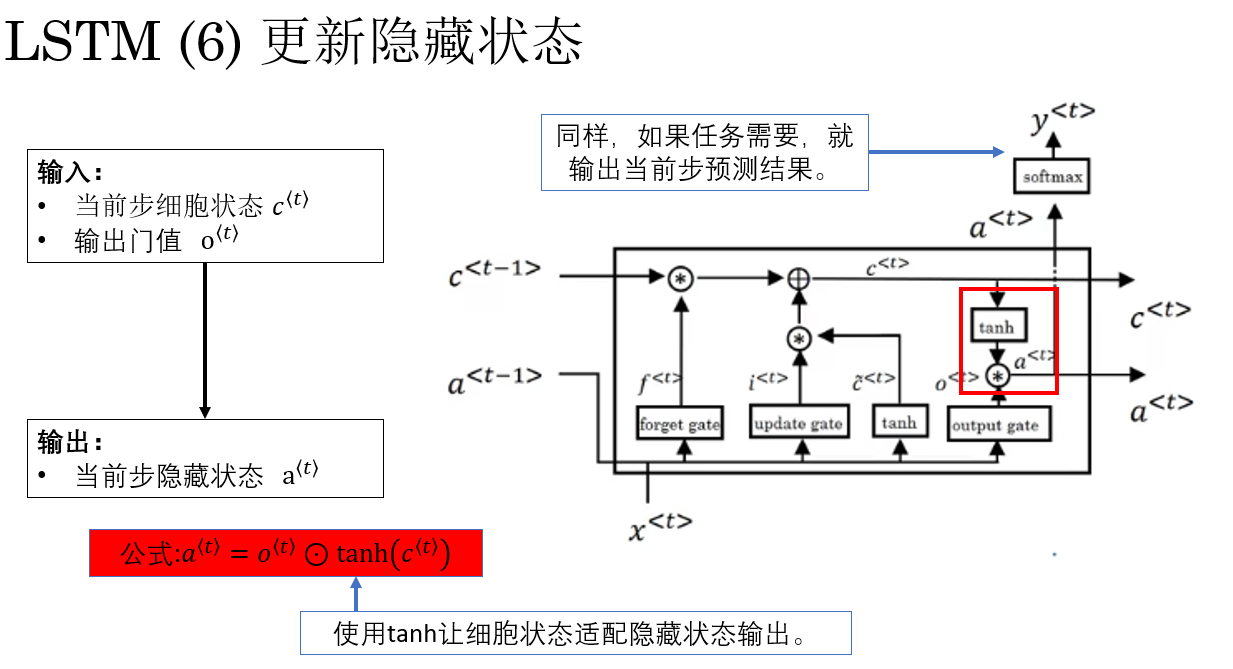
生成公式为：

\[a^{\langle t \rangle} = o^{\langle t \rangle} \odot \tanh(c^{\langle t \rangle}) \]

最终，输出门与细胞状态、隐藏状态维度一致，每个分量独立控制对应记忆单元的输出 ，实现对长期记忆的选择性读取 。

最后，看到长期记忆，你可能会再次想到 GRU 中不仅有长期记忆，还有短期记忆，那 LSTM 的短期记忆被隐含在哪一步了？

实际上，在 LSTM 中，短期记忆 就是当前步的隐藏状态 \(a^{\langle t \rangle}\)，它会传给下一时间步或下一层参与计算，而不像 GRU 那样把长期记忆和短期记忆合并在同一状态中。

至此，一个 LSTM 单元计算就完成了。

3.7 小结：LSTM 的完整计算流程

在时间步 \(t\)，一个标准 LSTM 单元的计算顺序可以总结为：

遗忘门：决定旧记忆保留多少。

\[ f^{\langle t \rangle} = \sigma(W_{xf} x^{\langle t \rangle} + W_{af} a^{\langle t-1 \rangle} + b_f) \]

输入门：决定新信息写入多少。

\[ i^{\langle t \rangle} = \sigma(W_{xi} x^{\langle t \rangle} + W_{ai} a^{\langle t-1 \rangle} + b_i) \]

候选记忆：生成新记忆内容。

\[ \tilde{c}^{\langle t \rangle} = \tanh(W_{xc} x^{\langle t \rangle} + W_{ac} a^{\langle t-1 \rangle} + b_c) \]

更新细胞状态：长期记忆融合。

\[ c^{\langle t \rangle} = f^{\langle t \rangle} \odot c^{\langle t-1 \rangle} + i^{\langle t \rangle} \odot \tilde{c}^{\langle t \rangle} \]

输出门与隐藏状态：生成当前输出。

\[o^{\langle t \rangle} = \sigma(W_{xo} x^{\langle t \rangle} + W_{ao} a^{\langle t-1 \rangle} + b_o) \]

\[ a^{\langle t \rangle} = o^{\langle t \rangle} \odot \tanh(c^{\langle t \rangle}) \]

至此，这两篇我们完成了对门控机制的一些相关技术的了解，你会发现，门控机制并没有创新网络本身的结构，而是通过网络关系和计算逻辑为全连接层赋予了全新的语义：实现了对记忆的选择性保留、更新与输出 。

这种设计的巧妙之处在于：网络可以自主决定哪些信息值得长期记忆，哪些信息只用于当前计算，使梯度在时间维度上稳定传播，同时让模型能够精细管理短期与长期记忆，从而显著提升序列数据建模的能力。

同时，也给了我们关于创新的新的灵感：不要一味增加复杂结构，而是赋予已有机制新的语义与控制能力。

3. 总结

概念	原理	比喻
LSTM（Long Short-Term Memory）	为了解决 RNN/GRU 在长序列中长期依赖的问题，引入显式的记忆单元（cell state），并配合遗忘门、输入门、输出门进行精细控制，实现长期信息的稳定传递。	隐藏状态像"当前脑子里在想什么"，细胞状态像"一本几乎不被打扰的长期备忘录"。
GRU 的局限	GRU 只有单一隐藏状态，既承担短期计算，又承担长期记忆，使不同时间尺度的信息混合在同一向量中，长序列或精细时序场景可能受限。	GRU 像是在"一张纸上反复修改内容"，长期与短期信息混合存储。
细胞状态（Cell State \(c^{\langle t \rangle}\)）	专门存储长期信息，可近似线性传播，梯度不易消失。通过遗忘门控制保留，输入门控制写入。	"长期备忘录"，可以长期保存关键信息，不被频繁改写。
隐藏状态（Hidden State \(a^{\langle t \rangle}\)）	表示当前时刻的输出和短期计算结果，传递到下一时间步或下一层。	"脑子里当前正在处理的内容"。
遗忘门（Forget Gate \(f^{\langle t \rangle}\)）	决定旧记忆保留比例：\(f^{\langle t \rangle} \odot c^{\langle t-1 \rangle}\)。	"决定把哪些旧信息保留下来，哪些丢掉"。
输入门（Input Gate \(i^{\langle t \rangle}\)）	决定新信息写入比例：\(i^{\langle t \rangle} \odot \tilde{c}^{\langle t \rangle}\)。	"决定新记忆写入多少到长期备忘录"。
候选细胞状态（\(\tilde{c}^{\langle t \rangle}\)）	当前步生成的新信息，由当前输入与上一隐藏状态计算，但尚未写入细胞状态。	"准备好可以写入的新记忆"。
更新细胞状态（\(c^{\langle t \rangle}\)）	结合遗忘门与输入门更新长期记忆：\(c^{\langle t \rangle} = f^{\langle t \rangle} \odot c^{\langle t-1 \rangle} + i^{\langle t \rangle} \odot \tilde{c}^{\langle t \rangle}\)。	"旧备忘录保留多少 + 新信息写入多少"。
输出门（Output Gate \(o^{\langle t \rangle}\)）	决定细胞状态暴露给隐藏状态的比例：\(a^{\langle t \rangle} = o^{\langle t \rangle} \odot \tanh(c^{\langle t \rangle})\)。	"决定长期记忆中哪些内容现在被使用"。
短期记忆	LSTM 的短期记忆即当前时刻的隐藏状态 \(a^{\langle t \rangle}\)，用于计算当前输出和下一步传递。	"脑子里当前想的东西"。
长期记忆	LSTM 的长期记忆即细胞状态 \(c^{\langle t \rangle}\)，稳定传递关键历史信息，梯度不易消失。	"长期备忘录"，可跨时间步保存信息。

吴恩达深度学习课程五：自然语言处理 第一周：循环神经网络 （六）长短期记忆 LSTM