竖直四子棋 - 技术栈

一、题目描述

竖直四子棋的棋盘是竖立起来的，双方轮流选择棋盘的一列下子，棋子因重力落到棋盘底部或者其他棋子之上，当一列的棋子放满时，无法再在这列上下子。

一方的4个棋子横、竖或者斜方向连成一线时获胜。

现给定一个棋盘和红蓝对弈双方的下子步骤，判断红方或蓝方是否在某一步获胜。

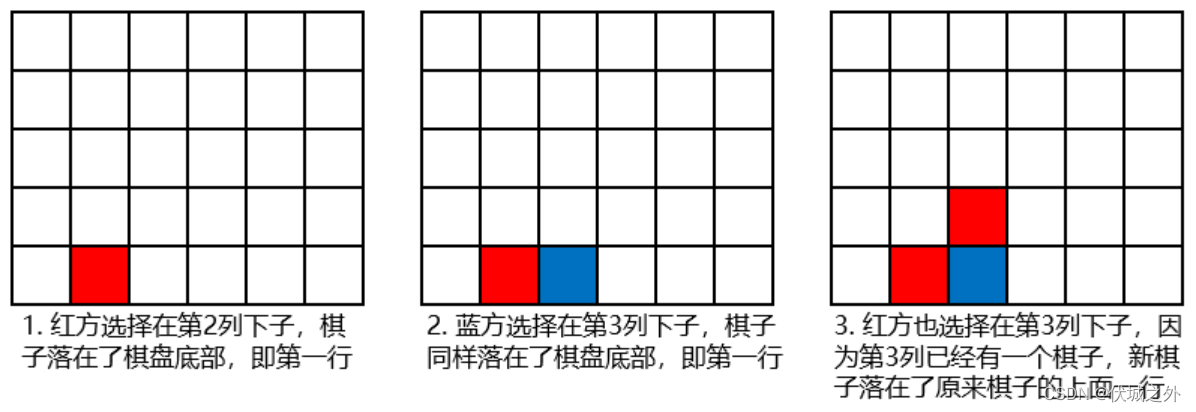
下面以一个6×5的棋盘图示说明落子过程：

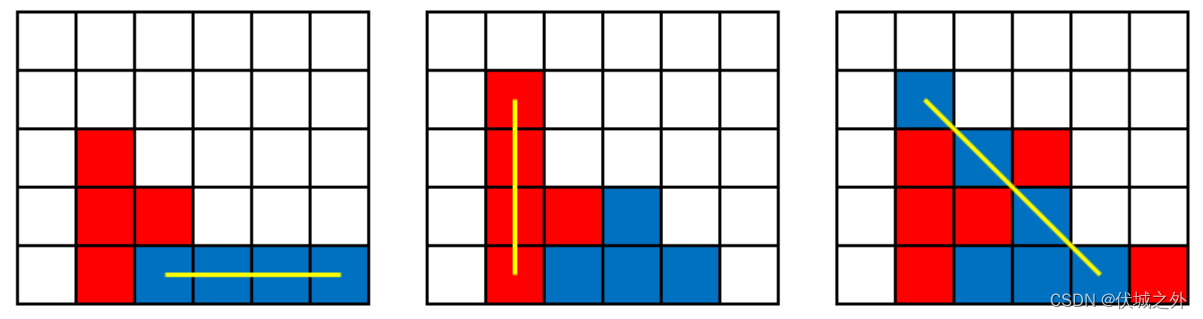
下面给出横、竖和斜方向四子连线的图示：

二、输入输出描述

输入描述

第一行：由空格分隔的两个整数，表示棋盘的宽和高；
第二行：由空格分隔的一组整数，每个数字为落子的列的编号（最左边的列编号为1，往右递增），同时也表示红蓝双方的落子步骤，第1步为红方的落子，第2步为蓝方的落子，第3步为红方的落子，以此类推。

输出描述

如果落子过程中红方获胜，输出 N,red ；

如果落子过程中蓝方获胜，输出 N,blue ；

如果出现非法的落子步骤，输出 N,error。

N为落子步骤的序号，从1开始。如果双方都没有获胜，输出 0,draw 。

非法落子步骤有两种，一是列的编号超过棋盘范围，二是在一个已经落满子的列上落子。

N和单词red、blue、draw、error之间是英文逗号连接。

三、示例

|----|-------------------------------------------------|
| 输入 | 5 5 1 1 2 2 3 3 4 4 |
| 输出 | 7,red |
| 说明 | 在第7步，红方在第4列落下一子后，红方的四个子在第一行连成一线，故红方获胜，输出 7,red。 |

|----|-----------------------------------|
| 输入 | 5 5 0 1 2 2 3 3 4 4 |
| 输出 | 1,error |
| 说明 | 第1步的列序号为0，超出有效列编号的范围，故输出 1,error。 |

四、解题思路

核心思想

采用逐步模拟落子 + 即时合法性校验 + 定向连线判定的策略，按顺序模拟每一步落子，先校验落子合法性（非法则终止），合法落子后检查是否形成四子连线（获胜则终止），最终根据过程输出结果。核心是 "模拟真实落子规则，定向检查减少计算量，即时终止提升效率"。

问题本质分析

表层问题：模拟四子棋落子过程，判断落子合法性与获胜结果；
深层问题：

落子模拟的真实性：需实现 "重力落子"（棋子落到列最下方空位置），符合四子棋的物理规则；
合法性校验的即时性：每一步落子后先校验合法性，非法则立即终止并输出结果，无需后续计算；
连线判定的高效性：仅检查落子位置的 4 条直线（而非全局），且仅当步数≥7 时触发，减少无效计算；
方向覆盖的完整性：通过 4 个基础方向 + 反方向，覆盖所有可能的四子连线方向（竖、横、两条对角线），无遗漏。
核心逻辑

输入解析：读取棋盘规格和落子列序列；
逐步落子：

合法性校验：列号是否合法、列是否已满，非法则返回错误；
重力落子：找到列最下方的空位置，标记当前玩家的棋子；
获胜判定：步数≥7 时，检查落子位置的 4 条直线是否有四子连线，有则返回获胜结果；

结果输出：所有落子完成后无获胜 / 错误，返回平局。

步骤拆解
输入预处理
- 读取棋盘规格（n 列 m 行）和落子列序列；
- 初始化棋盘数组（维度[m+1][n+1]，索引 0 闲置）。
逐步落子处理对每一步落子（索引 i，对应第 i+1 步）：
- 步骤 1：校验列号是否在[1,n]范围内，非法则输出 "i+1,error" 并终止；
- 步骤 2：确定当前玩家（红方 / 蓝方）；
- 步骤 3：从列的最底部（第 m 行）往上找空位置，若列已满则输出 "i+1,error" 并终止；
- 步骤 4：在空位置标记当前玩家的棋子；
- 步骤 5：若步数≥7，调用isFour方法检查四子连线：
  - 遍历 4 个基础方向，每个方向检查其反方向，统计同色棋子长度；
  - 任意方向长度≥4，输出 "i+1,red/blue" 并终止；
平局处理
- 所有落子完成且无非法 / 获胜，输出 "0,draw"。

五、代码实现

java 复制代码

import java.util.Arrays;
import java.util.Scanner;

public class Main {
  public static void main(String[] args) {
    Scanner sc = new Scanner(System.in);

    int[] tmp = Arrays.stream(sc.nextLine().split(" ")).mapToInt(Integer::parseInt).toArray();
    int n = tmp[0];
    int m = tmp[1];

    int[] cols = Arrays.stream(sc.nextLine().split(" ")).mapToInt(Integer::parseInt).toArray();

    System.out.println(getResult(n, m, cols));
  }

  /**
   * @param n 宽 ，矩阵列数
   * @param m 高，矩阵行数
   * @param cols 落子的列的编号
   */
  public static String getResult(int n, int m, int[] cols) {
    int r = m;
    int c = n;

    // 构造棋盘，注意棋盘长宽都+1了，方便后面棋子获取
    int[][] matrix = new int[r + 1][c + 1];

    // 这里i对应第几步，由于题目是从第1步开始算，而这里 i 从0开始算，因此最终返回要i+1
    for (int i = 0; i < cols.length; i++) {
      // cols[i]代表第 i 步下在第几列
      if (cols[i] < 1 || cols[i] > c) return i + 1 + ",error";

      // player落子颜色：1代表红色，2代表蓝色
      int player = i % 2 == 0 ? 1 : 2;

      // 落子逻辑
      int x = m;
      int y = cols[i];
      while (matrix[x][y] > 0) {
        x--; // 如果当前列底部有棋子，则需要往上查找
        if (x < 1) return i + 1 + ",error"; // 如果当前列已经放满棋子，则报错
      }
      matrix[x][y] = player; // 如果当前列底部没有棋子，则可以放入

      // i >= 6，即第七步及之后落子时，才可能产生四连击
      if (i >= 6 && isFour(x, y, player, matrix, r, c)) {
        return i + 1 + "," + (player == 1 ? "red" : "blue");
      }
    }

    // 双方都没有获胜
    return "0,draw";
  }

  // 上，左，左上，左下
  static int[][] offsets = {{-1, 0}, {0, -1}, {-1, -1}, {-1, 1}};

  public static boolean isFour(int x, int y, int player, int[][] matrix, int r, int c) {
    for (int[] offset : offsets) {
      int len = 1;

      // 向着某个方向延申判断是否存在相同子
      int x1 = x, y1 = y;
      while (true) {
        x1 += offset[0];
        y1 += offset[1];

        if (x1 >= 1 && x1 <= r && y1 >= 1 && y1 <= c && matrix[x1][y1] == player) {
          len++;
        } else {
          break;
        }
      }

      // 向着上面方向的反方向延申判断是否存在相同子（两个相反方向其实处于一条线上）
      int x2 = x, y2 = y;
      while (true) {
        x2 -= offset[0];
        y2 -= offset[1];

        if (x2 >= 1 && x2 <= r && y2 >= 1 && y2 <= c && matrix[x2][y2] == player) {
          len++;
        } else {
          break;
        }
      }

      // 如果此线可以形成四子连击，则直接返回true
      if (len >= 4) return true;
    }

    return false;
  }
}