介绍
相机是结构光、飞行时间(ToF)等3D传感技术中获取光信息的核心工具。本文从光学与计算机视觉的基础原理出发,系统阐述3D成像技术中的相机模型,将其拆解为三个核心模块:
-
几何成像模型:描述三维场景向二维图像的几何映射过程;
-
辐射度量模型:表征场景亮度向像素辐射照度的辐射量化传递过程;
-
光子转移模型:揭示像素接收的辐射照度转换为图像灰度的物理机制,并完成相机噪声建模。
深入理解这三个模型,对3D测量系统设计、深度与点云的精准重建,以及测距精度的优化提升具有至关重要的意义。
一、相机构成
在展开相机模型的详细介绍前,首先明确相机的核心构成:镜头、滤光片与图像传感器是组成相机光学系统与感光系统的三大关键部件。
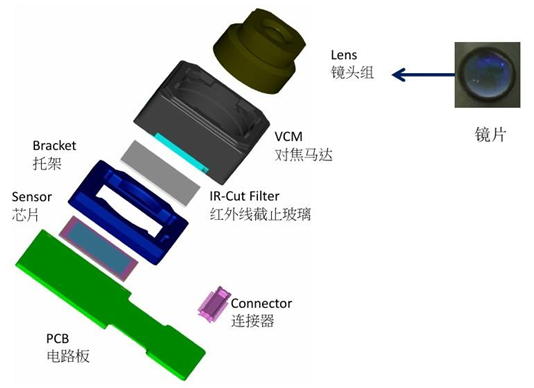
1.1 镜头
镜头的核心作用是收集场景反射的光线,并将其精准聚焦于图像传感器上,形成清晰的光学影像。其功能可概括为两点:一是"聚光",通过多片光学镜片的组合,汇聚不同方向的散射光线,确保充足光量到达传感器;二是"成像矫正",优质镜头会采用非球面镜、低色散镜等特殊镜片修正光学畸变,使聚焦后的影像更贴近真实场景的几何形态。
镜头的核心参数为焦距( f f f)与光圈F数( F F F)。在图像传感器尺寸固定时,焦距越长,视场角越小,成像放大倍数越大,适用于远距离拍摄;焦距越短,视场角越大,可容纳更广场景,适用于广角成像。光圈F数定义为镜头有效焦距与入瞳有效直径的比值( F = f / D F = f/D F=f/D),是无量纲参数,也是描述镜头通光能力、控制进光量与景深的关键指标。当焦距f固定时,F数越小,入瞳面积越大,通光能力越强;反之,F数越大,通光能力越弱。
1.2 滤光片
滤光片位于镜头与图像传感器之间,核心功能是选择性过滤光线,仅允许特定波长的光线到达传感器,从而优化成像效果、消除干扰光。根据过滤波长的差异,常用滤光片可分为可见光滤光片与红外滤光片两大类:
-
可见光滤光片:广泛应用于消费级相机(手机、单反等),核心作用是过滤对彩色成像无用的红外光------由于图像传感器本身对红外光敏感,若不过滤会导致色彩严重偏差(如画面偏红、偏暖)。这类滤光片仅允许400~760nm波长的可见光通过,确保传感器接收的光线与人类视觉系统感知一致,还原真实色彩;部分专业型号还可进一步减少眩光、提升色彩饱和度。
-
红外滤光片:与可见光滤光片功能相反,可过滤可见光,仅允许特定波长(如850nm、940nm)的红外光通过,主要用于红外成像场景。在3D视觉领域,由于通常采用红外波段光源,配合红外带通滤光片可有效降低环境光干扰,提升信号稳定性。
1.3 图像传感器
CMOS(Complementary Metal-Oxide-Semiconductor,互补金属氧化物半导体)图像传感器是相机的"核心感光部件",其作用是将镜头聚焦后的光学信号转换为电信号,经后续放大量化后生成数字图像的灰度信息。相较于传统CCD(电荷耦合器件)传感器,CMOS传感器具有功耗低、集成度高、成本低的优势,现已成为主流相机(手机、单反、工业相机)的首选感光器件。
图像传感器的核心参数包括分辨率(水平与竖直方向的像素数量)、像素大小、量子效率、暗噪声水平等。
二、几何成像模型
相机的核心功能是将三维物理空间中的物体投射为二维图像平面的像素信息,而几何成像模型正是连接三维空间与二维图像的关键桥梁。本节从基础的单透镜成像规律出发,引入景深、超焦距概念,再逐步展开计算机视觉中的针孔模型与畸变模型。
2.1 单透镜成像
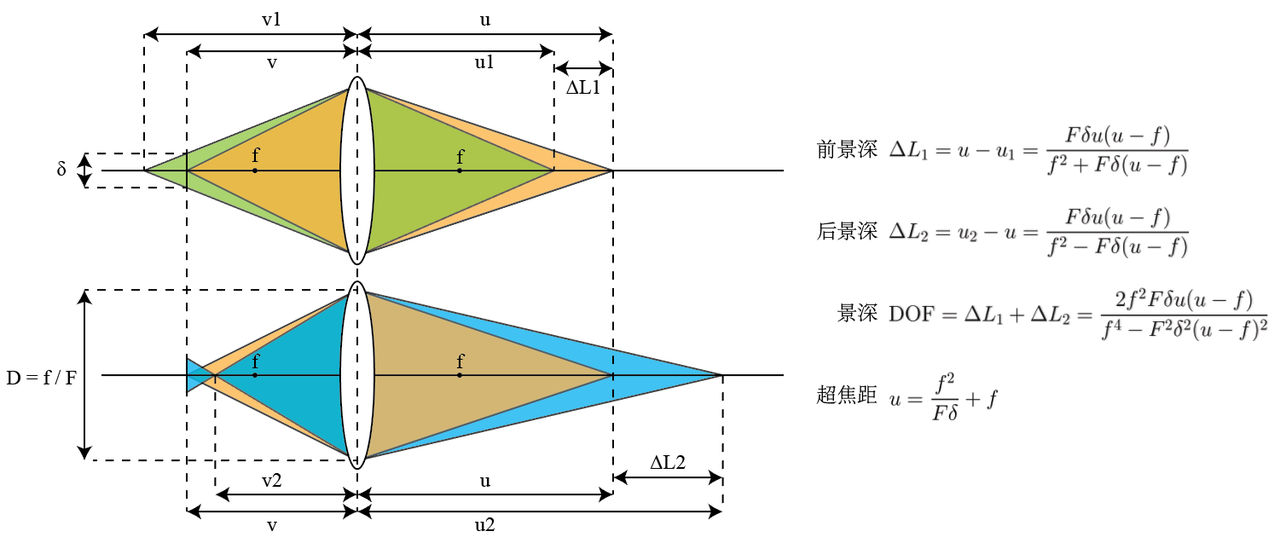
对于焦距为 f f f、光阑直径为 D D D、F数为 F = f / D F=f/D F=f/D的透镜,若图像传感器位于像距 v v v处,根据高斯成像公式 1 u + 1 v = 1 f \frac{1}{u} + \frac{1}{v} = \frac{1}{f} u1+v1=f1,可推导得出清晰成像的物距为 u = f v v − f u = \frac{fv}{v-f} u=v−ffv。需注意的是,未处于对应像距的点,在传感器靶面会弥散形成圆形光斑,即弥散圆。
若规定靶面允许的弥散圆直径为 δ \delta δ,根据三角形相似原理,可推导得出清晰成像对应的两个临界像距:
v 1 = D v D − δ , v 2 = D v D + δ v_1=\frac{Dv}{D-\delta}, \quad v_2=\frac{Dv}{D+\delta} v1=D−δDv,v2=D+δDv对应的临界物距为:
u 1 = f v 1 v 1 − f , u 2 = f v 2 v 2 − f u_1=\frac{fv_1}{v_1-f}, \quad u_2=\frac{fv_2}{v_2-f} u1=v1−ffv1,u2=v2−ffv2基于临界物距,可定义前景深 Δ L 1 \Delta L_1 ΔL1与后景深 Δ L 2 \Delta L_2 ΔL2:
Δ L 1 = u − u 1 = F δ u ( u − f ) f 2 + F δ ( u − f ) \Delta L_1 = u-u_1=\frac{F\delta u(u-f)}{f^2+F\delta(u-f)} ΔL1=u−u1=f2+Fδ(u−f)Fδu(u−f) Δ L 2 = u 2 − u = F δ u ( u − f ) f 2 − F δ ( u − f ) \Delta L_2 = u_2-u=\frac{F\delta u(u-f)}{f^2-F\delta(u-f)} ΔL2=u2−u=f2−Fδ(u−f)Fδu(u−f)景深(Depth of Field, DOF)则为前景深与后景深之和: DOF = Δ L 1 + Δ L 2 = 2 f 2 F δ u ( u − f ) f 4 − F 2 δ 2 ( u − f ) 2 \text{DOF} = \Delta L_1+\Delta L_2 = \frac{2f^2F\delta u(u-f)}{f^4-F^2\delta^2(u-f)^2} DOF=ΔL1+ΔL2=f4−F2δ2(u−f)22f2Fδu(u−f)当后景深趋于无穷大时, u 1 u_1 u1之后的所有点均可清晰成像,此时的对焦距离 u u u称为超焦距(Hyperfocal Distance)。令 Δ L 2 → ∞ \Delta L_2 \to \infty ΔL2→∞,可推导得出: f 2 = F δ ( u − f ) ⟹ u = f 2 F δ + f f^2=F\delta(u-f) \implies u = \frac{f^2}{F\delta}+f f2=Fδ(u−f)⟹u=Fδf2+f在3D测量中,需确保被测物体处于相机景深范围内。事实上,除条纹结构光系统外,散斑结构光、ToF等多数3D测量系统在设计时均处于超焦距状态。以iToF相机为例,若镜头焦距 f = 2.6 mm f=2.6\ \text{mm} f=2.6 mm、光圈 F = 1.2 F=1.2 F=1.2,图像传感器像素大小为 5 μ m 5\ \mu\text{m} 5 μm,允许的弥散圆直径为2个像素(即 δ = 10 μ m \delta=10\ \mu\text{m} δ=10 μm),代入公式计算可得超焦距约为 566 mm 566\ \text{mm} 566 mm。此时将相机对焦于该距离,从 283 mm 283\ \text{mm} 283 mm(超焦距的1/2)到无穷远的物体均可清晰成像,且传感器对应的像距约为 2.612 mm 2.612\ \text{mm} 2.612 mm,近似等于焦距。
2.2 针孔模型
计算机视觉中的针孔模型是单透镜成像模型的简化与抽象,其核心假设是被测物体位于景深范围内,可忽略镜头光圈导致的成像弥散。由于3D测量时相机对焦距离通常远大于焦距,此时像距 v ≈ f v \approx f v≈f,针孔模型直接将传感器置于焦距位置,用焦距替代像距;同时,假定成像平面位于镜头光心前的焦点处,避免透镜倒置成像引入的正负号繁琐表述。
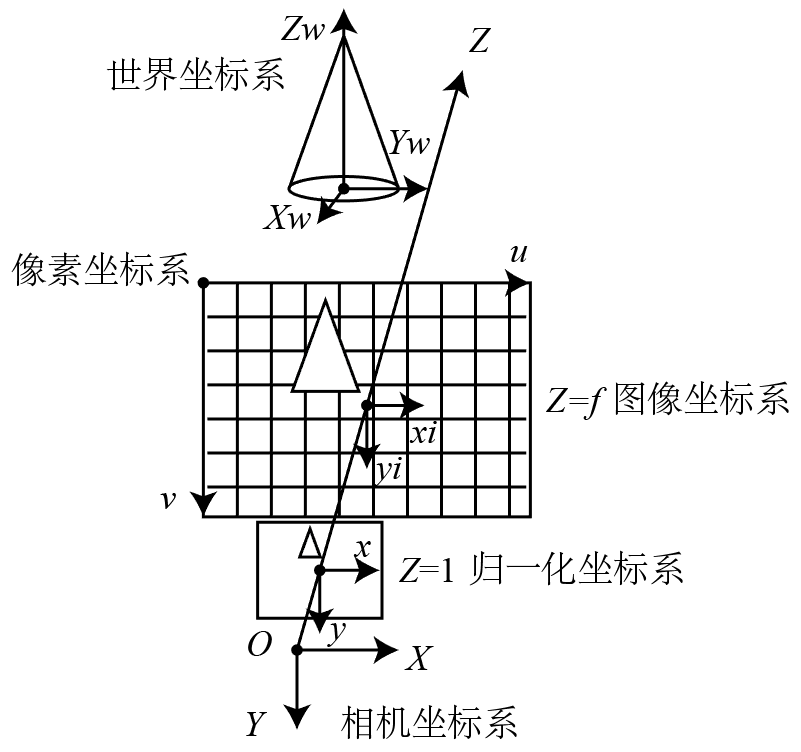
针孔模型涉及五个坐标系:世界坐标系、相机坐标系、归一化坐标系、图像坐标系与像素坐标系,其中相机坐标系、归一化坐标系与像素坐标系是核心坐标系,各坐标系定义如下:
世界坐标系与相机坐标系:均为三维坐标系。世界坐标系是公共坐标基准,位置与姿态可任意定义,用于统一不同物体与相机的三维坐标。若世界坐标系在相机坐标系中的姿态由旋转矩阵 R R R与平移矩阵 T T T描述,则世界坐标系中的点 P w = [ X w , Y w , Z w ] T P_w=[X_w,Y_w,Z_w]^T Pw=[Xw,Yw,Zw]T转换为相机坐标系中的点 P = [ X , Y , Z ] T P=[X,Y,Z]^T P=[X,Y,Z]T的关系为: [ X Y Z ] = [ r 11 r 12 r 13 r 21 r 22 r 23 r 31 r 32 r 33 ] [ X w Y w Z w ] + [ t 1 t 2 t 3 ] \begin{bmatrix}X\\Y\\Z\end{bmatrix}=\begin{bmatrix}r_{11}&r_{12}&r_{13}\\r_{21}&r_{22}&r_{23}\\r_{31}&r_{32}&r_{33}\end{bmatrix}\begin{bmatrix}X_w\\Y_w\\Z_w\end{bmatrix}+\begin{bmatrix}t_1\\t_2\\t_3 \end{bmatrix} XYZ = r11r21r31r12r22r32r13r23r33 XwYwZw + t1t2t3 相机坐标系的 Z Z Z轴为成像光轴, X X X轴平行于传感器水平方向(向右为正), Y Y Y轴平行于传感器竖直方向(向下为正),相机通过透视投影将相机坐标系中的三维点映射至垂直于 Z Z Z轴的二维平面。
归一化坐标系、图像坐标系与像素坐标系:均为二维坐标系, X X X轴与 Y Y Y轴方向与相机坐标系一致。
- 归一化坐标系位于相机坐标系 Z = 1 Z=1 Z=1平面,原点为光轴与该平面的交点。相机坐标系中的点经透视投影后,在归一化坐标系中的坐标为 x = X Z , y = Y Z x = \frac{X}{Z}, \ y = \frac{Y}{Z} x=ZX, y=ZY;
- 图像坐标系位于相机坐标系 Z = f Z=f Z=f平面,原点为光轴与该平面的交点。相机坐标系中的点经透视投影后,在图像坐标系中的坐标为 x i = f ⋅ X Z = f ⋅ x , y i = f ⋅ Y Z = f ⋅ y x_i = f\cdot\frac{X}{Z} = f \cdot x, \ y_i = f\cdot\frac{Y}{Z} = f \cdot y xi=f⋅ZX=f⋅x, yi=f⋅ZY=f⋅y
- 像素坐标系位于相机坐标系 Z = f Z=f Z=f平面,原点为传感器左上角像素中心。设水平与竖直方向的像素大小为 Δ x , Δ y \Delta_x,\Delta_y Δx,Δy,光轴与像素坐标系的交点(主点)坐标为 ( c x , c y ) (c_x,c_y) (cx,cy),则像素坐标系与图像坐标系、归一化坐标系的转换关系为: u = x i Δ x + c x = f Δ x ⋅ x + c x , v = y i Δ y + c y = f Δ y ⋅ y + c y u = \frac{x_i}{\Delta_x}+c_x = \frac{f}{\Delta_x}\cdot x+c_x, \quad v = \frac{y_i}{\Delta_y}+c_y = \frac{f}{\Delta_y}\cdot y+c_y u=Δxxi+cx=Δxf⋅x+cx,v=Δyyi+cy=Δyf⋅y+cy定义 f x = f / Δ x , f y = f / Δ y f_x=f/\Delta_x, f_y=f/\Delta_y fx=f/Δx,fy=f/Δy为针孔模型中水平与竖直方向的像素焦距,上述转换过程可表示为齐次矩阵形式:
u v 1 \] ⋍ \[ f x 0 c x 0 f y c y 0 0 1 \] \[ r 11 r 12 r 13 t 1 r 21 r 22 r 23 t 2 r 31 r 32 r 33 t 3 \] \[ X w Y w Z w 1 \] \\begin{bmatrix}u\\\\v\\\\1\\end{bmatrix}\\backsimeq\\begin{bmatrix}f_x\&0\&c_x\\\\0\&f_y\&c_y\\\\0\&0\&1\\end{bmatrix}\\begin{bmatrix}r_{11}\&r_{12}\&r_{13}\&t_1\\\\r_{21}\&r_{22}\&r_{23}\&t_2\\\\r_{31}\&r_{32}\&r_{33}\&t_3\\end{bmatrix}\\begin{bmatrix}X_w\\\\Y_w\\\\Z_w\\\\1\\end{bmatrix} uv1 ⋍ fx000fy0cxcy1 r11r21r31r12r22r32r13r23r33t1t2t3 XwYwZw1 其中 ⋍ \\backsimeq ⋍表示透视投影后的等价关系,即左侧向量等于右侧矩阵运算结果向量除以其最后一个元素。
针孔模型是理想的几何成像抽象,假定直线经透视投影后仍为直线,但实际镜头存在光学畸变,导致直线投影后发生弯曲,这一现象无法通过针孔模型表征。畸变模型是修正这一偏差的关键数学工具,与针孔模型共同构成相机真实成像的完整几何描述。
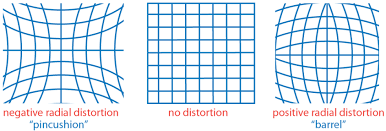
Brown畸变模型由Brown D.C.于1966年提出,是融合径向畸变与切向畸变的联合模型,也是计算机视觉与机器视觉领域描述镜头几何畸变的经典模型。该模型能精准拟合绝大多数普通光学镜头的畸变特性,是相机标定(如张正友标定法)的核心基础,也是3D成像与视觉测量中畸变校正的关键依据。
Brown模型定义于归一化坐标系,将畸变拆解为径向畸变与切向畸变两部分,通过多项式公式量化偏差,实现畸变的数学描述与矫正。其中,径向距离 r r r定义为归一化坐标到原点的距离,即 r 2 = x 2 + y 2 r^2 = x^2 + y^2 r2=x2+y2。
- 径向畸变:由镜头镜片的球面加工误差与装配偏差导致,呈径向对称分布,偏差量由关于径向距离的奇次多项式描述:
{ Δ x r a d = x ⋅ ( k 1 r 2 + k 2 r 4 + k 3 r 6 ) Δ y r a d = y ⋅ ( k 1 r 2 + k 2 r 4 + k 3 r 6 ) \begin{cases} \Delta x_{rad} = x \cdot (k_1 r^2 + k_2 r^4 + k_3 r^6) \\ \Delta y_{rad} = y \cdot (k_1 r^2 + k_2 r^4 + k_3 r^6) \end{cases} {Δxrad=x⋅(k1r2+k2r4+k3r6)Δyrad=y⋅(k1r2+k2r4+k3r6)式中 k 1 , k 2 , k 3 k_1, k_2, k_3 k1,k2,k3为径向畸变系数,根据系数符号可分为两种畸变类型:桶形畸变(Barrel Distortion): k 1 < 0 k_1 < 0 k1<0,图像向中心收缩,边缘被压缩,常见于广角镜头;枕形畸变(Pincushion Distortion): k 1 > 0 k_1 > 0 k1>0,图像从中心向外拉伸,边缘被放大,常见于长焦镜头。 - 切向畸变:由镜头镜片装配不平行(光轴与像平面不垂直)或镜片非球面误差导致,呈非径向对称分布,表现为像素的切向偏移,影响通常小于径向畸变,偏差量由关于径向距离的二次多项式描述: { Δ x t a n = 2 p 1 x y + p 2 ( r 2 + 2 x 2 ) Δ y t a n = p 1 ( r 2 + 2 y 2 ) + 2 p 2 x y \begin{cases} \Delta x_{tan} = 2p_1 x y + p_2 (r^2 + 2x^2) \\ \Delta y_{tan} = p_1 (r^2 + 2y^2) + 2p_2 x y \end{cases} {Δxtan=2p1xy+p2(r2+2x2)Δytan=p1(r2+2y2)+2p2xy式中 p 1 , p 2 p_1, p_2 p1,p2为切向畸变系数,分别描述不同方向的切向偏移偏差。
将径向畸变与切向畸变的偏差量叠加,可得Brown模型的核心公式:
{ x d i s t = x + Δ x r a d + Δ x t a n = x ( 1 + k 1 r 2 + k 2 r 4 + k 3 r 6 ) + 2 p 1 x y + p 2 ( r 2 + 2 x 2 ) y d i s t = y + Δ y r a d + Δ y t a n = y ( 1 + k 1 r 2 + k 2 r 4 + k 3 r 6 ) + p 1 ( r 2 + 2 y 2 ) + 2 p 2 x y \begin{cases} x_{dist} = x + \Delta x_{rad} + \Delta x_{tan} = x(1 + k_1 r^2 + k_2 r^4 + k_3 r^6) + 2p_1 x y + p_2 (r^2 + 2x^2) \\ y_{dist} = y + \Delta y_{rad} + \Delta y_{tan} = y(1 + k_1 r^2 + k_2 r^4 + k_3 r^6) + p_1 (r^2 + 2y^2) + 2p_2 x y \end{cases} {xdist=x+Δxrad+Δxtan=x(1+k1r2+k2r4+k3r6)+2p1xy+p2(r2+2x2)ydist=y+Δyrad+Δytan=y(1+k1r2+k2r4+k3r6)+p1(r2+2y2)+2p2xy模型的核心参数为 k 1 , k 2 , k 3 k_1, k_2, k_3 k1,k2,k3(径向畸变系数)与 p 1 , p 2 p_1, p_2 p1,p2(切向畸变系数),共5个参数。将归一化坐标系的畸变后坐标 x d i s t , y d i s t x_{dist}, y_{dist} xdist,ydist代入针孔模型,即可得到从三维空间点到畸变像素坐标的完整映射:
{ u d i s t = f x ⋅ x d i s t + c x v d i s t = f y ⋅ y d i s t + c y \begin{cases} u_{dist} = f_x \cdot x_{dist} + c_x \\ v_{dist} = f_y \cdot y_{dist} + c_y \end{cases} {udist=fx⋅xdist+cxvdist=fy⋅ydist+cy相机的像素焦距 f x , f y f_x,f_y fx,fy、主点坐标 c x , c y c_x,c_y cx,cy,以及径向畸变系数 k 1 , k 2 , k 3 k_1, k_2, k_3 k1,k2,k3、切向畸变系数 p 1 , p 2 p_1, p_2 p1,p2共同构成相机内参,是针孔+畸变模型的核心参数,可通过相机标定实验获取。关于相机标定的原理与C++代码实现,可参考【张正友标定法解析与C++代码实现】、【基于三维标定物的相机标定】。其它畸变模型,还有迭代去畸变算法,可以参考【相机畸变:Brown-Conrady、Kanala-Brandt畸变模型与迭代去畸变】
三、辐射度量模型
3.1 辐射度量学基础概念
阐述相机辐射度量模型前,需明确辐射度量学的核心概念,下表汇总了关键术语的定义、单位与核心关系(详细内容可参考笔者此前的辐射度量学博客【辐射度量学基础概念汇总】):
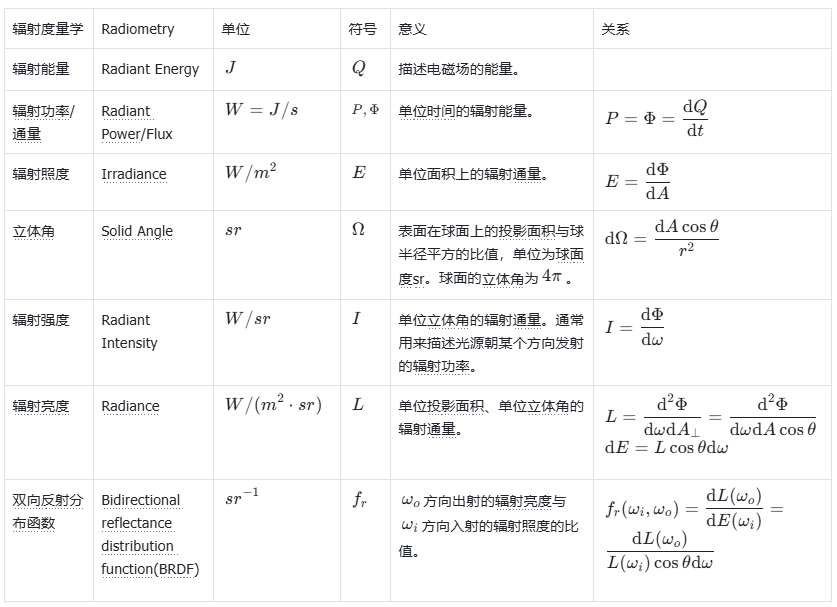
借助上述概念,可定量描述3D传感中"光源发光---物体反射---相机成像"的完整光信号传递过程,具体分为两个核心阶段:物体表面反射光线的辐射亮度计算,以及相机对反射光线的收集与辐射照度转换。
3.2 物体表面反射光线的辐射亮度
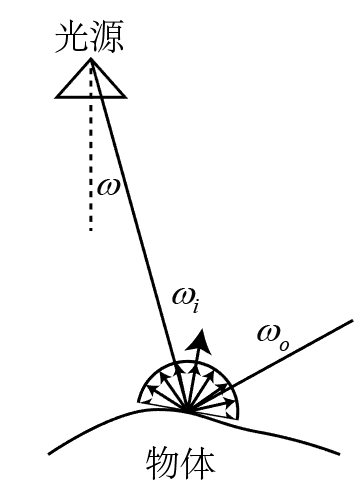
光源的核心辐射参数为辐射通量 P P P,表征单位时间内发射的总辐射能量。光源朝某一方向 ω \omega ω的辐射特性由辐射强度 I ( ω ) I(\omega) I(ω)描述,即该方向 d ω \text{d}\omega dω立体角内的辐射通量 d P \text{d}P dP,对全空间积分可得到总辐射通量: P = ∫ I ( ω ) d ω P = \int I(\omega)\text{d}\omega P=∫I(ω)dω设光源到物体表面某点的距离为 d d d,光源方向与该点表面法向的夹角为 ω i \omega_i ωi,则光源在该点产生的入射辐射照度为: E i = I ( ω ) cos ( ω i ) d 2 E_i = \frac{I(\omega)\cos(\omega_i)}{d^2} Ei=d2I(ω)cos(ωi)若该点的双向反射分布函数为 f r ( ω i , ω o ) f_r(\omega_i,\omega_o) fr(ωi,ωo)( ω o \omega_o ωo为反射方向),则其朝 ω o \omega_o ωo方向反射的光线辐射亮度为: L o = E i ⋅ f r ( ω i , ω o ) L_o=E_i\cdot f_r(\omega_i,\omega_o) Lo=Ei⋅fr(ωi,ωo)
3.3 相机对反射光线的收集与辐射照度
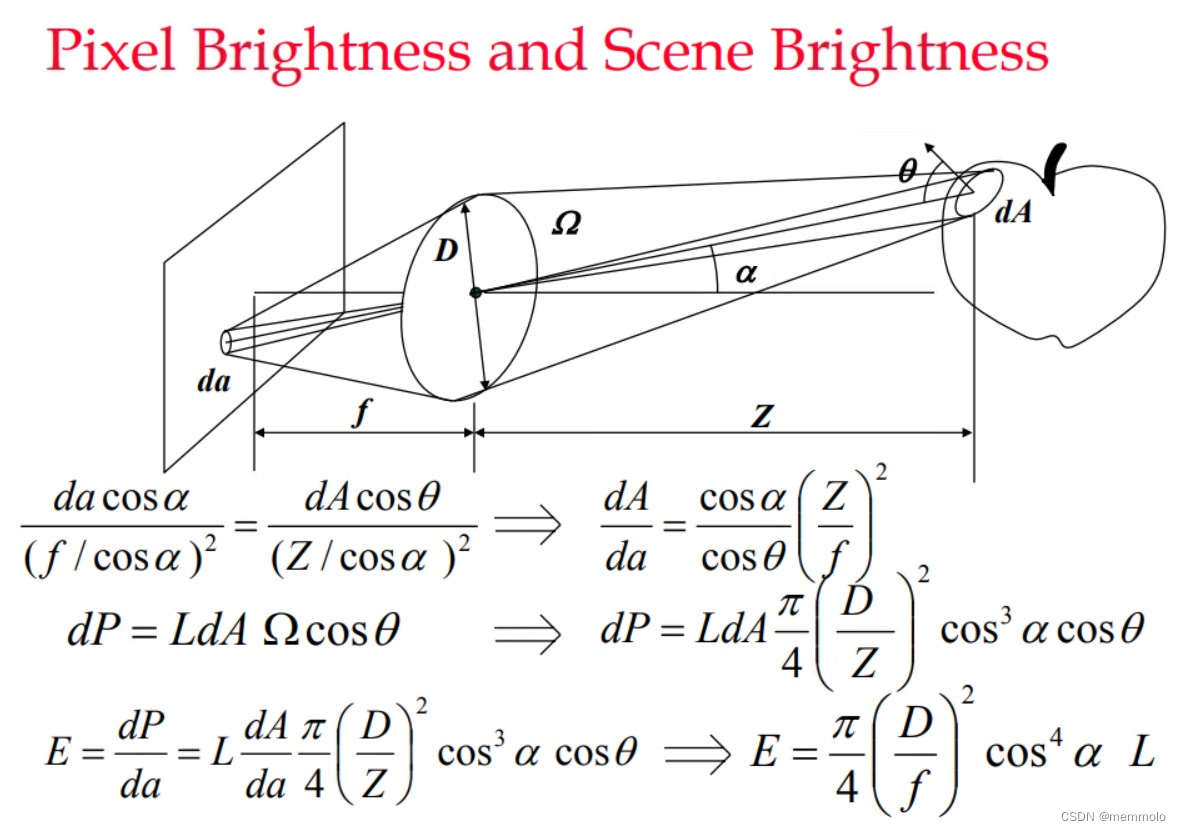
设物体表面微元面积为 d A \text{d}A dA,反射光线与表面法向的夹角为 θ \theta θ,与相机光轴的夹角为 α \alpha α,物体到相机光心的光轴方向距离为 Z Z Z。根据三角形相似原理,该微元在焦距为 f f f的相机传感器靶面上对应的成像面积 d a \text{d}a da为:
d a = f 2 cos θ Z 2 cos α d A \text{d}a = \frac{f^2\cos\theta}{Z^2\cos{\alpha}}\text{d}A da=Z2cosαf2cosθdA对于光阑直径为 D D D的镜头,其对物体表面微元所张的立体角 Ω \Omega Ω为:
Ω = π D 2 4 ⋅ cos α ( Z / cos α ) 2 = π 4 ( D Z ) 2 cos 3 α \Omega = \frac{\frac{\pi D^2}{4}\cdot\cos\alpha}{(Z/\cos\alpha)^2}=\frac{\pi}{4}(\frac{D}{Z})^2\cos^3\alpha Ω=(Z/cosα)24πD2⋅cosα=4π(ZD)2cos3α镜头在光阑处收集的辐射通量 d P \text{d}P dP,等于垂直于光线方向的微元面积( d A cos θ \text{d}A\cos\theta dAcosθ)、辐射亮度 L L L与立体角 Ω \Omega Ω的乘积: d P = L ⋅ Ω ⋅ d A cos θ = L ⋅ π 4 ( D Z ) 2 cos 3 α ⋅ d A cos θ \text{d}P = L\cdot\Omega\cdot\text{d}A\cos\theta=L\cdot\frac{\pi}{4}(\frac{D}{Z})^2\cos^3\alpha\cdot\text{d}A\cos\theta dP=L⋅Ω⋅dAcosθ=L⋅4π(ZD)2cos3α⋅dAcosθ该辐射通量在靶面微元面积 d a \text{d}a da上产生的辐射照度 E E E为:
E = d P d a = π 4 ( D f ) 2 cos 4 α ⋅ L E = \frac{\text{d}P}{\text{d}a}=\frac{\pi}{4}(\frac{D}{f})^2\cos^4\alpha\cdot L E=dadP=4π(fD)2cos4α⋅L
由上述公式可得出核心结论:像素接收的辐射照度与物体距离 Z Z Z无关,仅与反射光线的辐射亮度 L L L呈线性正相关;结合光圈F数定义 F = f / D F=f/D F=f/D,可知辐射照度与 F 2 F^2 F2呈反比(F数越小,通光能力越强,辐射照度越高);理想情况下,辐射照度随反射光线与光轴夹角 α \alpha α呈 cos 4 \cos^4 cos4规律衰减,即边缘区域的辐射照度低于中心区域。
四、光子转移模型
光子转移模型基于EMVA1288标准,系统描述了相机将入射到图像传感器靶面的光子转化为数字图像灰度的物理过程,并对该过程中的各类噪声进行建模,是分析图像灰度波动与测距精度关系的核心依据。
4.1 物理转化过程
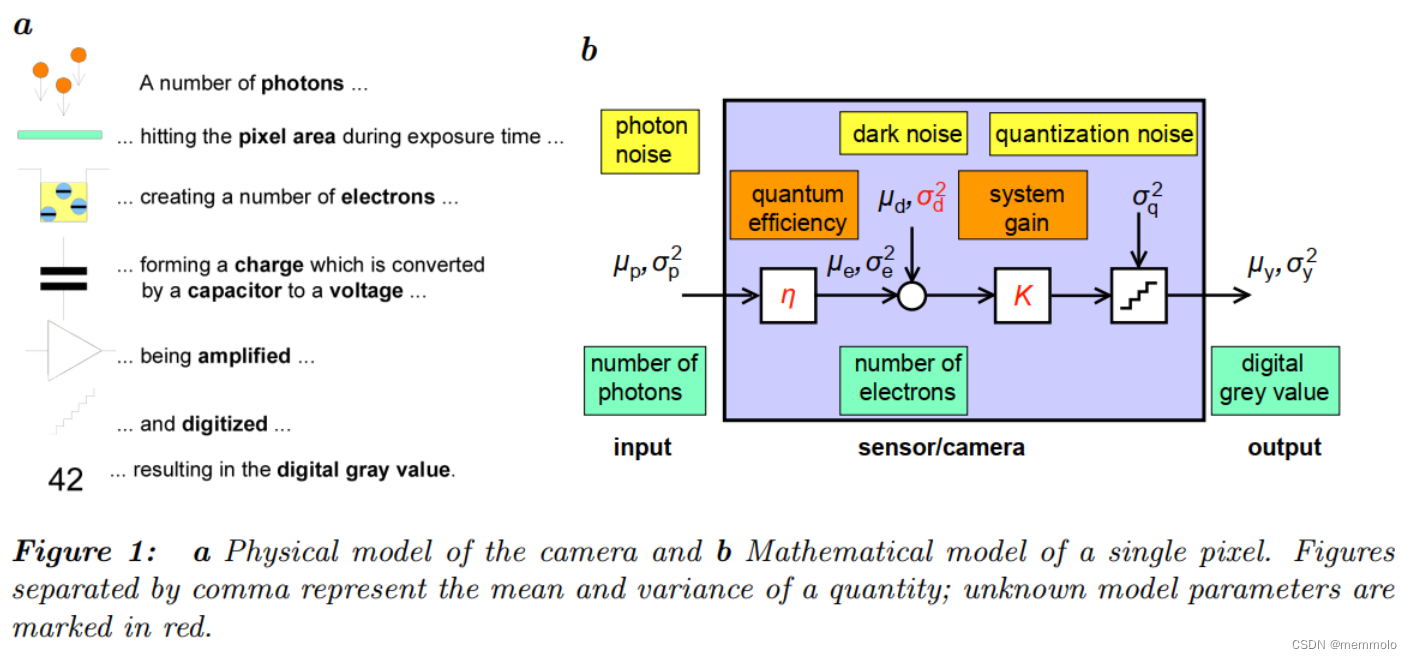
光子从入射到转化为图像灰度,需经历三个核心阶段:
- 光子到达像素后,通过光电效应转化为光生电子;
- 曝光时间内产生的光生电子被像素电容收集,形成电压信号;
- 电压信号经放大、模数转换(量化)后,生成数字图像的灰度值。
4.2 各阶段的定量建模
(1)光子数建模
曝光时间 t e x p t_{exp} texp内,到达单个像素的光子数期望为: μ p = A ⋅ E ⋅ t e x p h c / λ \mu_p=\frac{A\cdot E\cdot t_{exp}}{hc/\lambda} μp=hc/λA⋅E⋅texp式中, A A A为像素面积, E E E为像素接收的辐射照度, h h h为普朗克常量, c c c为光速, λ \lambda λ为入射光波长。由于光子的量子随机性,到达像素的光子数服从泊松分布,其方差等于期望,即 σ p 2 = μ p \sigma_p^2=\mu_p σp2=μp这种随机性导致的噪声称为散粒噪声。
(2)电子数建模
每个光子被转化为光生电子的概率称为量子效率( η \eta η),因此光生电子数的期望为: μ e = η ⋅ μ p \mu_e=\eta\cdot\mu_p μe=η⋅μp。光生电子数同样服从泊松分布,方差为 σ e 2 = μ e = η ⋅ μ p \sigma_e^2=\mu_e=\eta\cdot\mu_p σe2=μe=η⋅μp证明过程参考【EMVA1288 相机噪声模型】
(3)图像灰度建模
光生电子数 μ e \mu_e μe经系统增益 K K K(灰度/电子)缩放后,叠加相机暗信号 μ d a r k \mu_{dark} μdark(无光照时的灰度均值),最终输出图像灰度的期望 μ y \mu_y μy:
μ y = K ⋅ μ e + μ d a r k \mu_y=K\cdot\mu_e+\mu_{dark} μy=K⋅μe+μdark图像灰度的方差 σ y 2 \sigma_y^2 σy2由三部分组成:经增益缩放的散粒噪声方差、暗噪声方差 σ y , d a r k 2 \sigma_{y,dark}^2 σy,dark2(无光照时的灰度波动),以及量化噪声方差 σ q 2 = 1 / 12 \sigma_q^2=1/12 σq2=1/12(统计上呈均匀分布),即:
σ y 2 = K 2 ⋅ σ e 2 + σ y , d a r k 2 + σ q 2 \sigma_y^2=K^2\cdot\sigma_e^2+\sigma_{y,dark}^2+\sigma_q^2 σy2=K2⋅σe2+σy,dark2+σq2结合 σ e 2 = μ e \sigma_e^2=\mu_e σe2=μe与 μ e = μ y − μ d a r k K \mu_e=\frac{\mu_y-\mu_{dark}}{K} μe=Kμy−μdark,可推导得出灰度期望与方差的线性关系: σ y 2 = K ⋅ ( μ y − μ d a r k ) + σ y , d a r k 2 + σ q 2 \sigma_y^2=K\cdot(\mu_y-\mu_{dark})+\sigma_{y,dark}^2+\sigma_q^2 σy2=K⋅(μy−μdark)+σy,dark2+σq2利用这一线性关系,通过拟合灰度期望与方差的关系曲线,可求解系统增益 K K K,该方法称为光子转移法。
4.3 噪声对测距精度的影响
3D传感的测距结果通常由多帧或多个像素灰度值经非线性运算得到,若用函数 f f f表示灰度值到距离的映射关系( d = f ( y 1 , . . . , y N ) d = f(y_1,...,y_N) d=f(y1,...,yN), y 1 , . . . , y N y_1,...,y_N y1,...,yN为多帧或多个像素图像灰度),根据误差传递公式,测距结果的方差为:
σ d 2 = ∑ n ( ∂ f ∂ y n ) 2 σ y n 2 \sigma^2_d = \sum_n (\frac{\partial f}{\partial y_n})^2\sigma^2_{y_n} σd2=n∑(∂yn∂f)2σyn2该方差的大小直接表征测距精度,因此光子转移模型通过量化灰度噪声,为表征和优化3D测距精度提供了理论依据。