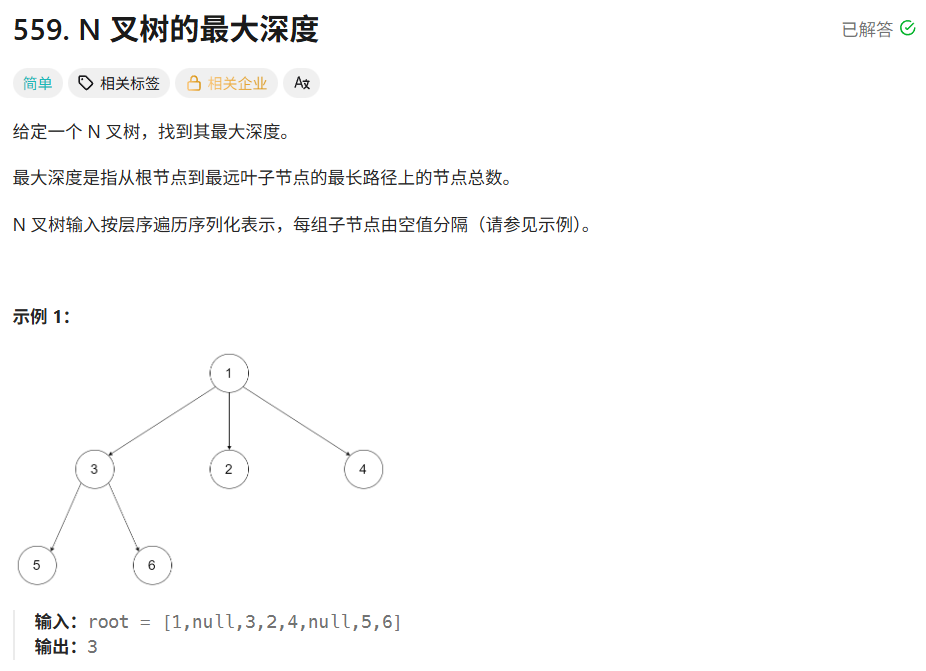
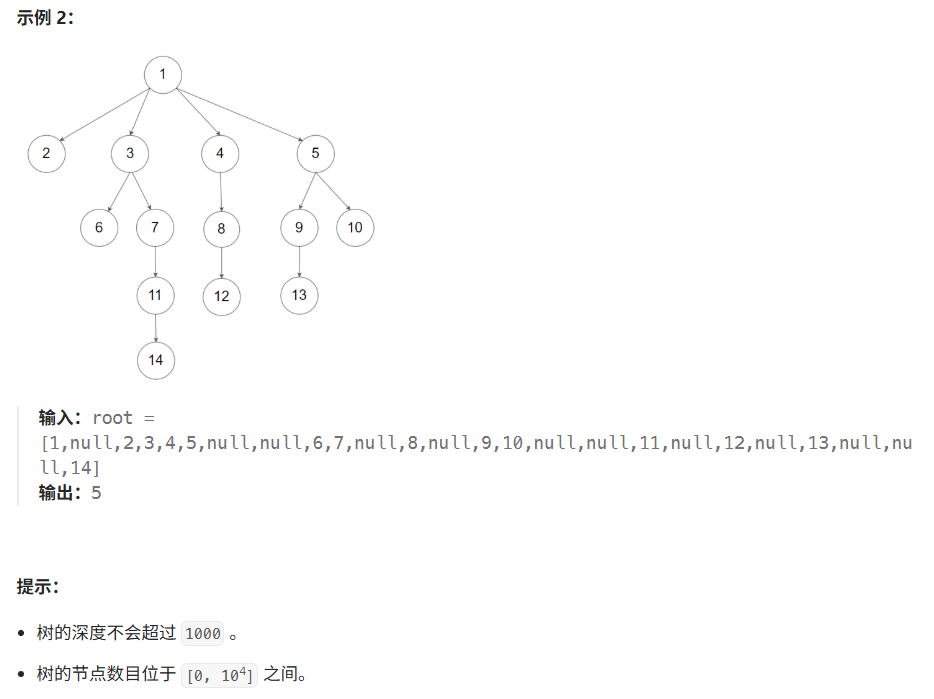
二叉树递归(后序遍历)
cpp
class Solution {
public:
// 计算N叉树的最大深度
int maxDepth(Node* root) {
// 递归终止条件:如果当前节点为空,深度为0
// 注意:这里用0表示空指针,通常写作nullptr更清晰
if (root == 0) return 0;
// 初始化当前节点的子树最大深度为0
int depth = 0;
// 遍历当前节点的所有子节点
for (int i = 0; i < root->children.size(); i++) {
// 递归计算每个子树的深度
// 更新depth为所有子树深度的最大值
depth = max (depth, maxDepth(root->children[i]));
}
// 返回当前节点的深度 = 子树最大深度 + 1
return depth + 1;
}
};-
if (root == 0) return 0;-
递归基准情况:空节点深度为0
-
在C++中,
0、NULL、nullptr都可以表示空指针 -
推荐使用
if (root == nullptr)或if (!root)更清晰
-
-
int depth = 0;-
初始化变量,用于记录当前节点的子节点中的最大深度
-
注意:这不是最终返回的深度,最终要加1
-
-
for (int i = 0; i < root->children.size(); i++)-
遍历当前节点的所有子节点
-
使用索引循环,也可以用范围for循环:
for (Node* child : root->children)
-
-
depth = max(depth, maxDepth(root->children[i]));-
递归计算每个子节点的深度
-
用
max函数不断更新找到的最大子节点深度 -
这行代码会递归展开整个子树
-
-
return depth + 1;-
关键步骤:当前节点的深度 = 子节点的最大深度 + 1
-
加1代表当前节点本身的一层深度
-
举例
1
/ | \
2 3 4
/ \ \
5 6 7步骤1:处理节点1
cpp
maxDepth(1):
if (1 == 0) return 0; // false,if语句不成立,继续执行下一行代码
int depth = 0; // depth = 0
// 开始分别遍历子节点 [2, 3, 4]
// 第【0】个子节点:节点2
for (int i = 0; i < 1->children.size(); i++): // i = 0
depth = max(depth, maxDepth(1->children[0])); // 调用 maxDepth(2)步骤2:处理节点2(递归调用)
cpp
maxDepth(2):
if (2 == 0) return 0; // false,直接执行下一条语句
int depth = 0; // depth = 0
// 遍历节点2的子节点 [5, 6]
// 第【0】个子节点:节点5
depth = max(depth, maxDepth(5)); // 调用 maxDepth(5)步骤3:处理节点5
cpp
maxDepth(5):
if (5 == 0) return 0; // false
int depth = 0; // depth = 0
// 遍历子节点:5->children.size() = 0 ,所以0<0不成立
// for循环不执行
return depth + 1; // return 0 + 1 = 1
// 节点5返回深度1所以maxDepth(5)=1
步骤4:继续处理节点2
cpp
// 回到 maxDepth(2):
depth = max(0, maxDepth(5)=1); // depth = max(0, 1) = 1
// for循环下一个子节点,第【1】节点:节点6
depth = max(1, maxDepth(6)); // 调用 maxDepth(6)步骤5:处理节点6
cpp
maxDepth(6):
if (6 == 0) return 0; // false
int depth = 0; // depth = 0
// 遍历子节点:6->children.size() = 0,0<0,所以不执行for循环
return depth + 1; // return 0 + 1 = 1
// 节点6返回深度1所以maxDepth(6)=1
步骤6:完成节点2的计算
cpp
// 回到 maxDepth(2):
depth = max(1, maxDepth(6)=1); // depth = max(1, 1) = 1
// 节点2的所有孩子节点均已遍历过,for循环结束
return depth + 1; // return 1 + 1 = 2
// 节点2返回深度2步骤7:回到节点1继续处理
cpp
// 回到 maxDepth(1):
depth = max(0, maxDepth(2)=2); // depth = max(0, 2) = 2
// 下一个子节点:节点3
depth = max(2, maxDepth(3)); // 调用 maxDepth(3)步骤8:处理节点3
cpp
maxDepth(3):
if (3 == 0) return 0; // false
int depth = 0; // depth = 0
// 遍历子节点:3->children.size() = 0
return depth + 1; // return 0 + 1 = 1
// 节点3返回深度1步骤9:继续处理节点1
cpp
// 回到 maxDepth(1):
depth = max(2, maxDepth(3)=1); // depth = max(2, 1) = 2
// 下一个子节点:节点4
depth = max(2, maxDepth(4)); // 调用 maxDepth(4)步骤10:处理节点4
cpp
maxDepth(4):
if (4 == 0) return 0; // false
int depth = 0; // depth = 0
// 遍历子节点 [7]
depth = max(depth, maxDepth(7)); // 调用 maxDepth(7)步骤11:处理节点7
cpp
maxDepth(7):
if (7 == 0) return 0; // false
int depth = 0; // depth = 0
return depth + 1; // return 0 + 1 = 1
// 节点7返回深度1步骤12:完成节点4的计算
cpp
// 回到 maxDepth(4):
depth = max(0, maxDepth(7)=1); // depth = max(0, 1) = 1
return depth + 1; // return 1 + 1 = 2
// 节点4返回深度2步骤13:完成节点1的计算
cpp
// 回到 maxDepth(1):
depth = max(2, maxDepth(4)=2); // depth = max(2, 2) = 2
// for循环结束,所有子节点处理完毕
return depth + 1; // return 2 + 1 = 3
// 节点1返回深度3maxDepth(1) = 3
├── maxDepth(2) = 2
│ ├── maxDepth(5) = 1
│ └── maxDepth(6) = 1
├── maxDepth(3) = 1
└── maxDepth(4) = 2
└── maxDepth(7) = 1最终结果 maxDepth(1) = 3
层序遍历
cpp
class Solution {
public:
int maxDepth(Node* root) {
queue<Node*> que;
if (root != NULL) que.push(root);
int depth = 0;
while (!que.empty()) {
int size = que.size();
depth++; // 记录深度
for (int i = 0; i < size; i++) {
Node* node = que.front();
que.pop();
for (int j = 0; j < node->children.size(); j++) {
if (node->children[j]) que.push(node->children[j]);
}
}
}
return depth;
}
};