能源之星案例

1 能源之星案例需求

能源之星（Energy Star），是一项由美国政府主导，主要针对消费性电子产品的能源节约计划。能源之星计划于1992年由美国环保署（EPA）和美国能源部(DOE)所启动，目的是为了降低能源消耗及减少温室气体排放。该计划后来又被澳大利亚、加拿大、日本、中国台湾、新西兰及欧盟采纳。该计划为自愿性，能源之星标准通常比美国联邦标准节能20-30%。最早配合此计划的产品主要是电脑等资讯电器，之后逐渐延伸到电机、办公室设备、照明、家电等等。后来还扩展到了建筑，美国环保署于1996年起积极推动能源之星建筑物计划，由环保署协助自愿参与业者评估其建筑物能源使用状况（包括照明、空调、办公室设备等）、规划该建筑物之能源效率改善行动计划以及后续追踪作业，所以有些导入环保新概念的住家或工商大楼中也能发现能源之星的标志。

某市公共可用建筑能源数据（建筑物能耗数据，涉及环保专业名词），使用能源数据建立一个模型，进行建筑能源利用率得分预测，简称能源之星(energy star score)评分，并剖析结果以找出影响评分的因素（分析特征和目标值关系，特征重要性）。

建筑物能耗数据简介：

地理位置
建筑物本身属性, 建筑年份, 物业性质(住宅, 酒店, 商业, 写字楼)
能耗情况(电力, 天然气, 燃油, 水)
用量(总量)
EUI 使用强度(单位面积用量，总量/单位面积)
温室气体排放
比较建筑物能效的相对度量
- Energy Star Score字段
- 根据年度报告中，能源使用情况进行1~100百分位排名，100最高分，得分越高（越好）越是能源之星
- 目标值是连续值，是一个回归问题

2 能源之星数据集介绍

通过程序认识能源数据

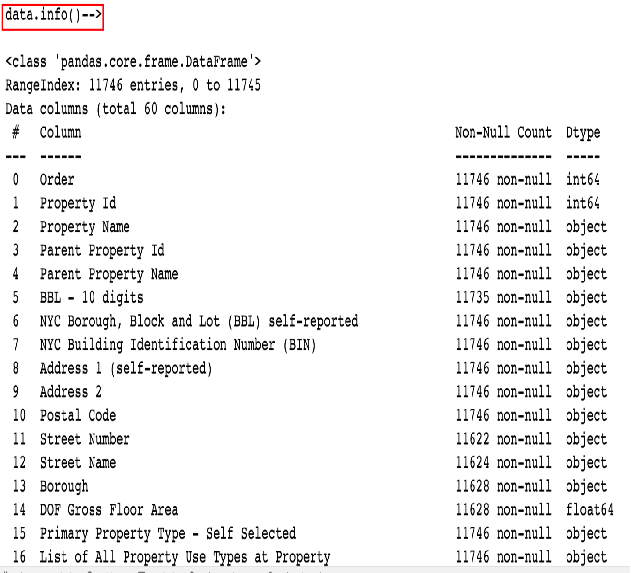
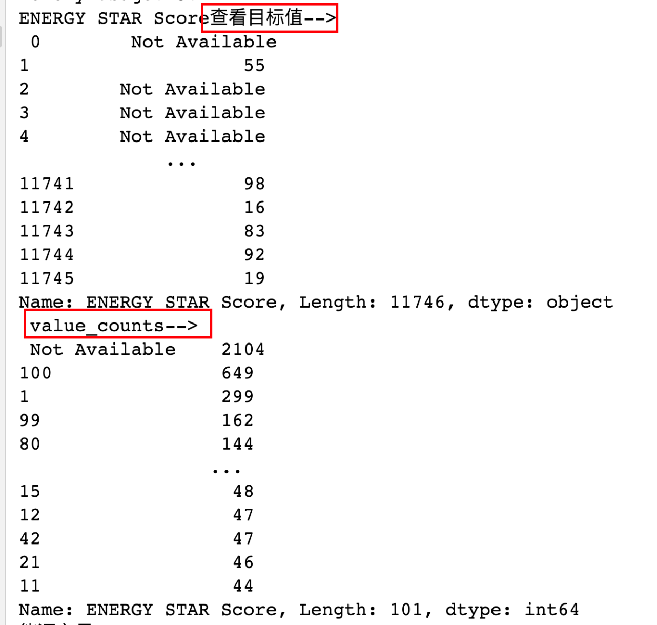
python 复制代码

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from IPython.core.pylabtools import figsize # 用来设置图片大小
import seaborn as sns
from sklearn.model_selection import train_test_split  # 训练集测试集划分
import warnings

warnings.filterwarnings('ignore')
# 设置显示所有列
# pd.set_option('display.max_columns', None)
sns.set(font_scale = 2)
plt.rcParams['font.size'] = 24 # 设置默认字体大小
def dm01_业务数据():
    # 1 加载数据
    data = pd.read_csv('data/Energy_and_Water_Data_Disclosure_for_Local_Law_84_2017__Data_for_Calendar_Year_2016_.csv')
    # 2 查看数据x
    print('data-->', data.shape) # (11746, 60)
    print('\ndata-->', data)
    print('data.describe-->\n', data.describe())
    print('data.info()-->\n') 
    data.info()
    # 3 查看数据y y存在缺失值/异常值
    print('ENERGY STAR Score查看目标值-->\n', data['ENERGY STAR Score'])
    print(' value_counts-->\n', data['ENERGY STAR Score'].value_counts())

字段介绍

python 复制代码

 0   Order                          11746 non-null  int64   唯一ID  
 1   Property Id                    11746 non-null  int64   地理位置  
 2   Property Name                  11746 non-null  object  地理位置     
 3   Parent Property Id             11746 non-null  object 
 4   Parent Property Name           11746 non-null  object 
 5   BBL - 10 digits                11735 non-null  object 
 6   NYC Borough, Block and Lot (BBL) self-reported 11746 non-null  object  属于那个区
 7   NYC Building Identification Number (BIN)       11746 non-null  object  区编号
 8   Address 1 (self-reported)      11746 non-null  object 
 9   Address 2                      11746 non-null  object 
 10  Postal Code                    11746 non-null  object 
 11  Street Number                  11622 non-null  object 
 12  Street Name                    11624 non-null  object 
 13  Borough                        11628 non-null  object  行政区
 14  DOF Gross Floor Area           11628 non-null  float64 以上是建筑地理位置信息
 15  Primary Property Type - Self Selected  11746 non-null  object  建筑类型基本属性自选
 16  List of All Property Use Types at Property   11746 non-null  object 
 17  Largest Property Use Type      11746 non-null  object  最大的应用场景
 18  Largest Property Use Type - Gross Floor Area (ft²)   11746 non-null  object 
 19  2nd Largest Property Use Type  11746 non-null  object 
 20  2nd Largest Property Use - Gross Floor Area (ft²)    11746 non-null  object 
 21  3rd Largest Property Use Type                        11746 non-null  object 
 22  3rd Largest Property Use Type - Gross Floor Area (ft²) 11746 non-null  object 
 23  Year Built                     11746 non-null  int64  
 24  Number of Buildings - Self-reported       11746 non-null  int64  
 25  Occupancy                      11746 non-null  int64  
 26  Metered Areas (Energy)         11746 non-null  object 
 27  Metered Areas  (Water)         11746 non-null  object 
 28  ENERGY STAR Score              11746 non-null  object 目标值 有异常值
 29  Site EUI (kBtu/ft²)            11746 non-null  object 能源使用强度 总量/面积
 30  Weather Normalized Site EUI (kBtu/ft²) 11746 non-null  object 天气能源使用强度
 31  Weather Normalized Site Electricity Intensity (kWh/ft²)   11746 non-null  object 电力能源使用强度
 32  Weather Normalized Site Natural Gas Intensity (therms/ft²)  11746 non-null  object 天然气能源使用强度
 33  Weather Normalized Source EUI (kBtu/ft²) 11746 non-null  object 水能源使用强度
 34  Fuel Oil  #1 Use (kBtu)        11746 non-null  object 使用汽油  
 35  Fuel Oil  #2 Use (kBtu)        11746 non-null  object  
 36  Fuel Oil  #4 Use (kBtu)        11746 non-null  object  
 37  Fuel Oil   #5 & 6 Use (kBtu)   11746 non-null  object  
 38  Diesel  #2 Use (kBtu)  柴油     11746 non-null  object  
 39  District Steam Use (kBtu)      11746 non-null  object 地区蒸汽使用量（kBtu）
 40  Natural Gas Use (kBtu)         11746 non-null  object 天然气使用量（kBtu）
 41  Weather Normalized Site Natural Gas Use (therms)  11746 non-null  object 天气标准化现场天然气使用
 42  Electricity Use - Grid Purchase (kBtu)    11746 non-null  object 电力使用-电网购买（kBtu）
 43  Weather Normalized Site Electricity (kWh) 11746 non-null  object 天气标准化现场电力（kWh）
 44  Total GHG Emissions (Metric Tons CO2e)    11746 non-null  object 温室气体排放总量
 45  Direct GHG Emissions (Metric Tons CO2e)   11746 non-null  object 直接GHG排放量
 46  Indirect GHG Emissions (Metric Tons CO2e) 11746 non-null  object 间接GHG排放量
 47  Property GFA - Self-Reported (ft²)        11746 non-null  int64  物业总建筑面积-自行报告
 48  Water Use (All Water Sources) (kgal)      11746 non-null  object 用水（所有水源）（kgal）
 49  Water Intensity (All Water Sources) (gal/ft²)  11746 non-null  object 水强度（所有水源）
 50  Source EUI (kBtu/ft²)             11746 non-null  object
 51  Release Date                      11746 non-null  object 发布日期
 52  Water Required?                   11628 non-null  object 需要水吗
 53  DOF Benchmarking Submission Status  11716 non-null  object 基准提交状态
 54  Latitude                          9483 non-null   float64 纬度
 55  Longitude                         9483 non-null   float64 经度
 56  Community Board                   9483 non-null   float64 社区委员会
 57  Council District                  9483 non-null   float64 议会选区
 58  Census Tract                      9483 non-null   float64 人口普查区
 59  NTA                               9483 non-null   object  国家统计局
dtypes: float64(6), int64(6), object(48)
memory usage: 5.4+ MB

3 能源之星机器学习工作流程

数据加载与清洗
- 熟悉业务和数据
- 清洗：缺失值, 异常值, 重复值
探索性数据分析（EDA）
- 探索目标值y、特征值x有无异常（通过直方图）eg：删除异常值
- 探索x和y的关系（线性关系或非线性关系，通过KDE图）
- x和x之间的关系，即计算特征相关性（通过散点图）
特征工程和选择
- 对数值型数据、离散值型数据处理
- 相关联非常近的特征挑选和删除
- 数据划分
比较不同机器学习模型
- 建立一个建立基线模型
- 4类模型：LR模型、训练随机森林模型、训练GBDT模型、训练KNN模型
对最佳模型执行超参数调整
- RandomizedSearchCV粗调
- GridSearchCV细调
最佳模型评估
- 默认模型和精调模型效果展示
模型结果解读
- 有的场景下, 模型只需要输出预测结果
- 有的场景下需给出业务建议来(特征重要性)

4 数据清洗

观察业务数据存在的问题:

很多数值类型的数据被处理成了object，需要处理
有些列数据缺失比例超过50%，需要处理

python 复制代码

#  缺失值的模板，通用的
#  定义一个函数，传进来一个DataFrame
def missing_values_table(df):
	# python的pandas库中有一个十分便利的isnull()函数,它可以用来判断缺失值,把每列的缺失值算一下总和
	mis_val = df.isnull().sum()

	# 100相当于%，每列的缺失值的占比
	mis_val_percent = mis_val / len(df) * 100

	# 每列缺失值的个数、每列缺失值的占比做成表
	mis_val_table = pd.concat([mis_val, mis_val_percent], axis=1)

	# 重命名指定列的名称
	mis_val_table_ren_columns = mis_val_table.rename(
		columns={0: 'Missing Values', 1: '% of Total Values'})

	# 对含有缺失值的列根据缺失值占比进行降序，从大到小
	mis_val_table_ren_columns = mis_val_table_ren_columns[
		mis_val_table_ren_columns['% of Total Values'] != 0].sort_values(
		'% of Total Values', ascending=False).round(1)
	return mis_val_table_ren_columns


def dm02_加载和清洗():
    # 1 加载数据 data(11746, 60)
    data = pd.read_csv('Energy_and_Water_Data_Disclosure_for_Local_Law_84_2017__Data_for_Calendar_Year_2016_.csv')
    # print('data.shape-->', data.shape)
    print('data.info-->1')
    data.info()
    # 2 数据类型转换.replace 'Not Available'替换成 np.nan, 把object转成float64
    data = data.replace({'Not Available':np.nan})
    # 2-1 # 遍历所有列, 处理本来是数值型,被当做object列 for col in list(data.columns)
    for col in data.columns:
        if ('ft²' in col or 'kBtu' in col or 'Metric Tons CO2e' in col or 'kWh' in
            col or 'therms' in col or 'gal' in col or 'Score' in col):
            # 转换成float类型
            data[col] = data[col].astype(float)
    # print('data.info-->2')
    data.info()
    # 3 缺失值处理, 删除缺失比例超过50%的列 missing_df[46, 2]
    # data.dropna(thresh=len(data)*0.5, axis=1, inplace=True)
    # 3-1 检索大于50%的列 missing_columns / missing_df[missing_df['% of Total Values'] > 50].index
    missing_df = missing_values_table(data)
    missing_columns = missing_df[missing_df['% of Total Values'] > 50].index
    print('缺失比例超过50%的列-->\n',missing_columns)
    # 3-2 data.drop( list(missing_columns) ), data(11746,60)-->data(11746,49) 删除了11列特征
    data = data.drop(columns=missing_columns)
    # 返回 修改数据类型 删除缺失比例超过50%的列的data
    return data

5 探索性数据分析EDA

探索性数据分析(Exploratory Data Analysis，EDA)概念：

主要工作：对数据进行清洗，对数据进行描述（描述统计量，图表），查看数据的分布，比较数据之间的关系，培养对数据的直觉，对数据进行总结等。
是数据分析或数据科学项目中的重要一步，调查数据集以发现关系和异常并根据我们对数据集的理解形成假设的过程。是一个开放式的话题

能源之星案例EDA的主要工作：

通过直方图探索目标值y、特征值x数值分布
通过四分位距(IQR)删除异常值
通过KDE图探索x和y的关系
通过相关系数和散点图计算x和x的相关性

5.1 删除异常值

IQR = 3/4分位数 - 1/4分位数

1/4分位数 - 3IQR 极小值的阈值；小于该阈值数据判断为异常

3/4分位数 + 3IQR 极大值的阈值；大于该阈值数据判断为异常

python 复制代码

def eda01_删除异常值(data):
    # 1 对目标值y画直方图分析, 重命名{'ENERGY STAR Score': 'score'}
    data = data.rename(columns={'ENERGY STAR Score': 'score'})  # 分数重命名
    
    # 2 画图 plt.hist(data['score'].dropna(), bins=100, edgecolor='k') figsize(8, 8)
    # 从直方图看1和100比例过高, 部分信息是自己上报的作弊的成分 plt.xlabel() .ylabel() .title()
    figsize(12, 8)
    plt.style.use('fivethirtyeight')
    plt.hist(data['score'].dropna(), bins=100, edgecolor='black')
    plt.xlabel('Score')
    plt.ylabel('Number of Buildings')
    plt.title('Energy Star Score Distribution')
    plt.show()
    
    # 3 绘制能源使用强度(EUI)，即总能源使用量/建筑面积
    # 3-1 能源使用强度的直方图.hist(data['Site EUI (kBtu/ft²)'].dropna(), bins=20, edgecolor='black')
    figsize(8, 8)
    plt.hist(data['Site EUI (kBtu/ft²)'].dropna(), bins=20, edgecolor='black')
    plt.xlabel('Site EUI')
    plt.ylabel('Count')
    plt.title('Site EUI Distribution')
    plt.show()
    # 3-2 从图中看, 数据中包含异常点
    # 查看描述信息data['Site EUI (kBtu/ft²)'].describe() / .dropna().sort_values().tail(10))
    print("data['Site EUI (kBtu/ft²)'].describe()-->\n", data['Site EUI (kBtu/ft²)'].describe())
    print('sort_values前10条数据\n', data['Site EUI (kBtu/ft²)'].dropna().sort_values().tail(10))
    # 查看data.loc[data['Site EUI (kBtu/ft²)'] == 869265, :] outlier_data信息
    outlier_data = data.loc[data['Site EUI (kBtu/ft²)'] == 869265, :]
    # print('Site EUI (kBtu/ft²) 异常点数据 outlier_data-->\n', outlier_data)
	
    # 4 通过四分位距(nterquartile range,IQR)-四分差识别异常值 删除异常值
    # 策略: IQR = 3/4分位数 - 1/4分位数; 1/4分位数- 3IQR 极小值的阈值; 3/4分位数+ 3IQR 极大值的阈值
    # 4-1 计算iqr, first_quartile, third_quartile, iqr / data['Site EUI (kBtu/ft²)'].describe()['25%']
    first_quartile = data['Site EUI (kBtu/ft²)'].describe()['25%']
    third_quartile = data['Site EUI (kBtu/ft²)'].describe()['75%']
    iqr = third_quartile - first_quartile # 计算iqr
    # 4-2 删除异常数据 # data(11746, 49) --> data(11319, 49)
    # 挑选符合条件的数据 EUI数据>(first_quartile - 3*iqr)) & EUE数据<(third_quartile + 3*iqr)
    # print('按照分位数处理数据之前data.shape', data.shape)  # (11746, 49)
    data = data[(data['Site EUI (kBtu/ft²)'] > (first_quartile - 3 * iqr)) &
                (data['Site EUI (kBtu/ft²)'] < (third_quartile + 3 * iqr))]
    # print('按照分位数处理数据后data.shape', data.shape)  # (11319, 49)
    # 4-3 再次绘制能源使用强度 (EUI)
    figsize(8, 8)
    plt.hist(data['Site EUI (kBtu/ft²)'].dropna(), bins=20, edgecolor='black')
    plt.xlabel('Site EUI')
    plt.ylabel('Count')
    plt.title('Site EUI Distribution')
    plt.show()
    
    # 5 返回最新data(11319, 49) score重命名/删除异常数据 
    return data

当前数据目标值y存在的问题
- Energy star score 是一个满分为100分的分数
- 按照能源使用效率从高到低排序。从直方图看出：1和100在所有的分数中比例过高
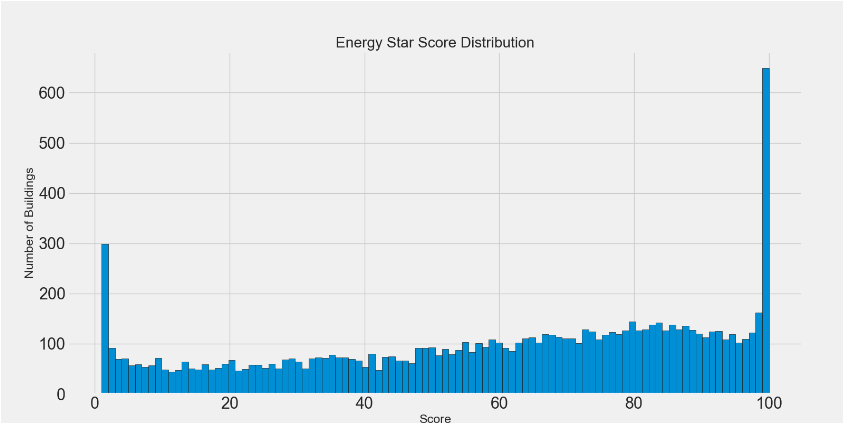
个别特征值x存在异常值问题
- 查看能源使用强度 (EUI)，即总能源使用量/建筑面积
- 该特征值存在异常值

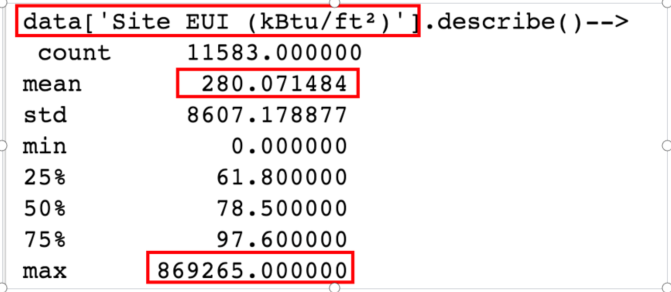
去掉异常值之后, EUI的数据接近正态分布，可以看到效果

说明：出现异常值的原因有很多：信息录入错误、测量设备故障、单位不正确，或者它们可能是合法但极端的值。在建模时要去掉异常值

5.2 探索特征值x与目标值y关系

python 复制代码

def eda02_特征值x与目标值y关系(data):
    # 1 探索最大物业特征['Largest Property Use Type']x与y的关系  data[11319,49]->types[,49]
    # 1-1 探索关系前,y的nan数据去除得types / data.dropna(subset=['score'])
    types = data.dropna(subset=['score'])  # 去除
    print('score列去除nan后的数据types-->1\n', types.shape)
    # 1-2 数据分组types / types['Largest Property Use Type'].value_counts()
    types = types['Largest Property Use Type'].value_counts()
    print('挑选分组types-->2\n', types)
    # 1-3 分组条目数大于100的分组 list(types[types.values > 100].index)
    # ['Multifamily Housing', 'Office', 'Hotel', 'Non-Refrigerated Warehouse'] : ['多户住宅'、'办公室'、'酒店'、'非冷藏仓库']
    types = types[types.values > 100].index
    print('挑选分组值大于100之后的types-->3\n', types)
    # 1-4 绘制每种类型的建筑与y(score)的KDE图
    # 准备4种建筑的数据,调用sns.kdeplot()函数 从图可看出,4种物业类型对sorce评分影响很大
    # 1-5 绘制4种建筑的KDE图
    figsize(12, 10)
    for b_type in types:
        # 选中不同建筑类型
        subset = data[data['Largest Property Use Type'] == b_type]
        # 绘制KDE图
        sns.kdeplot(subset['score'].dropna(), label=b_type)
    plt.xlabel('Energy Star Score', size=20)
    plt.ylabel('Density', size=20)
    plt.title('Density Plot of Energy Star Scores by Building Type', size=28)
    plt.legend()
    plt.show()
        
	# 2 探索自治市镇boroughs特征x与y之间的关系, KDE图
    # 2-1 探索关系前,y的nan数据去除得boroughs /data.dropna(subset=['score'])
    boroughs = data.dropna(subset=['score'])
    # 2-2 对数据分组boroughs / boroughs['Borough'].value_counts()
    boroughs = boroughs['Borough'].value_counts()  # 数据分组
    # 2-3 分组条目数大于100的分组
    boroughs = boroughs[boroughs.values > 100].index
    # print('boroughs挑选分组值大于100之后的types-->2\n', boroughs)
    # ['Manhattan', 'Brooklyn', 'Queens', 'Bronx', 'Staten Island'] # '曼哈顿'、'布鲁克林'、'皇后区'、'布朗克斯'、'斯塔滕岛'
    # 2-4 绘制每种类型的建筑与y(score)的KDE图
    # 2-5 绘制4种地区的KDE图
    # 准备4种地区的数据,调用sns.kdeplot()函数 从图可看出,4种地区对sorce评分影响不大
    figsize(12, 10)
    for borough in boroughs:
        subset = data[data['Borough'] == borough]
        sns.kdeplot(subset['score'].dropna(), label=borough)
    plt.xlabel('Energy Star Score', size=20)
    plt.ylabel('Density', size=20)
    plt.title('Density Plot of Energy Star Scores by Borough', size=28)
    plt.legend()
    plt.show()
    # 返回data data没有发生变化
    return data

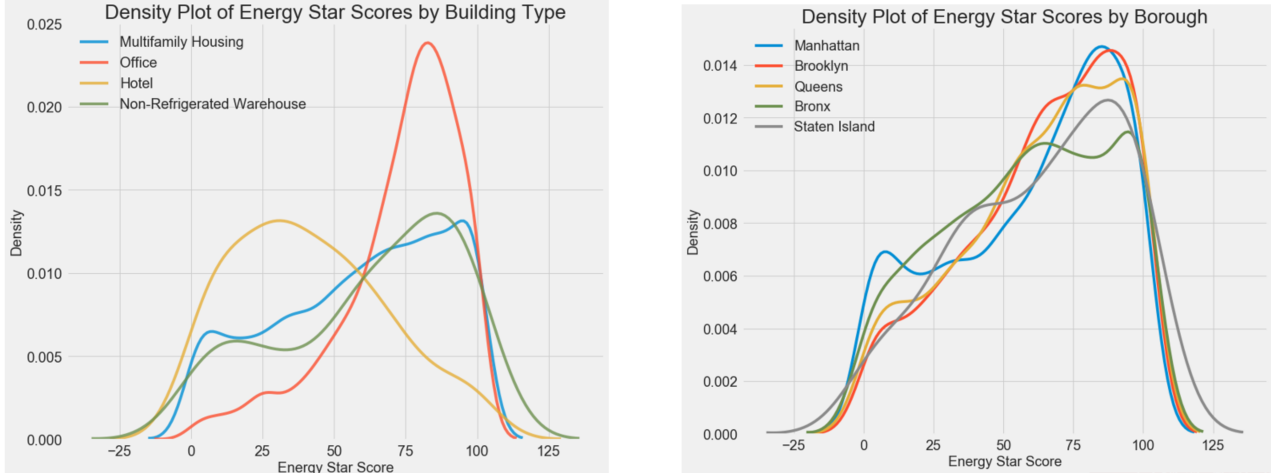
通过KDE图来查看特征值x和特征值y之间的关系，分析特征x对y的影响
- 可以查看数值型特征对y的影响，也可查看离散型数据对y的影响，KDE图连续变量中不同数值的概率密度。举个栗子：人的身高分布
- 本案例探索最大物业特征data['Largest Property Use Type']与y的KDE图
- 本案例探索自治市镇data['boroughs']特征与y的KDE图
- 从图分析：自治市镇特征对目标值y的影响没有最大物业特征大

5.3 计算相关性(皮尔逊相关系数)

python 复制代码

def eda03_计算相关性(data):
    # 1 计算两两数据相关性 eg:特征x与y的相关性correlations_data / data.corr()['score'].sort_values()
    # 分析数据可知:建筑能耗越大 sorce分越低 相当于越不环保 # print('两两数据相关性-->\n', data.corr())
    corr_data = data.select_dtypes('number').corr()['score'].sort_values()  # 数据排序
    corr_data.to_csv('111.csv')
    print('\ncorr_data-->\n', corr_data)  # 建筑能耗越大 建筑能源利用率得分越低
    # print('\ncorr_data.head(15)-->\n', corr_data.head(15))
    # print('\ncorr_data.tail(15)-->\n', corr_data.tail(15))
    
    # 2 探索特征值x与y是不是存在非线性关系 
    # 方法: 对每一列x特征求平方根和对数, 然后再观察相关系数变化, 相关系数变大说明x与y存在非线性关系
    # 2-1 numeric_subset 选择数值型特征 / data.select_dtypes('number')
    numeric_subset = data.select_dtypes('number')
    # 2-2 数值特征列做平方根和log变换 numeric_subset['sqrt_'+col]=np.sqrt(numeric_subset[col])
    for col in numeric_subset.columns:
        if col == 'score':
            next
        else:
            numeric_subset['sqrt_' + col] = np.sqrt(numeric_subset[col])
            numeric_subset['log_' + col] = np.log(numeric_subset[col])
            
    # 3-1 选择类别型特征 categorical_subset两个列data[['Borough', 'Largest Property Use Type']]
    categorical_subset = data[['Borough', 'Largest Property Use Type']]
    # 3-2 对类别型特征one-hot编码 / pd.get_dummies(categorical_subset)
    categorical_subset = pd.get_dummies(categorical_subset)
    
    # 4 数值型特征 和列表型特征拼接到一起features / pd.concat([numeric_subset, categorical_subset], axis=1)
    features = pd.concat([numeric_subset, categorical_subset], axis=1)
    # 4-2 去掉features中score为nan的行 [11319, 138] --> [9461, 138]f eatures.dropna(subset=['score'])
    features = features.dropna(subset=['score'])
    # 5 再次计算features中x和y的相关性 correlations / features.corr()['score'].dropna().sort_values()
    # 对比观察 corr_data2 和 corr_data 排序前后变化 corr_data.to_csv('1111.csv')
    # dropna():log(x<0)->nan 
    corr_data2 = features.corr()['score'].dropna().sort_values()
    print('corr_data2-->\n', corr_data2)
    # print('corr_data2.head(15)-->\n', corr_data2.head(15))
    # print('corr_data2.tail(15)-->\n', corr_data2.tail(15))
    corr_data2.to_csv('222.csv')
    
    # 6 观察数据 整体上数据排序没有发生多大变化
    # 6-1 相关性好的 plt.scatter(features['Site EUI (kBtu/ft²)'], features['score'])
    # figsize(12, 12)  # 用量越大 分数越低 有明显的线性相关性
    # plt.scatter(features['Site EUI (kBtu/ft²)'], features['score'])
    # plt.show()
    # 6-2 相关性不好的 plt.scatter(features['Weather Normalized Site Electricity Intensity (kWh/ft²)'], features['score'] )
    # figsize(12, 12)  # 相关性不是太好 但总体分数变化不大
    # plt.scatter(features['Weather Normalized Site Electricity Intensity (kWh/ft²)'], features['score'])
    # plt.show()
    
    # 7 实战经验: 若所有特征x和目标y之间的相关性没有超过30%, 做回归效果就不好; 想办法做出相关性比较强的特征
    # 返回 数值型和类别型组合在一起的特征 features [11319, 138] --> [9461, 138]
    return features

通过计算皮尔逊相关系数，量化特征（变量）与目标之间的相关性
- 观察数据能源使用强度 (EUI)、站点 EUI (kBtu/ft²)与目标值y最负相关
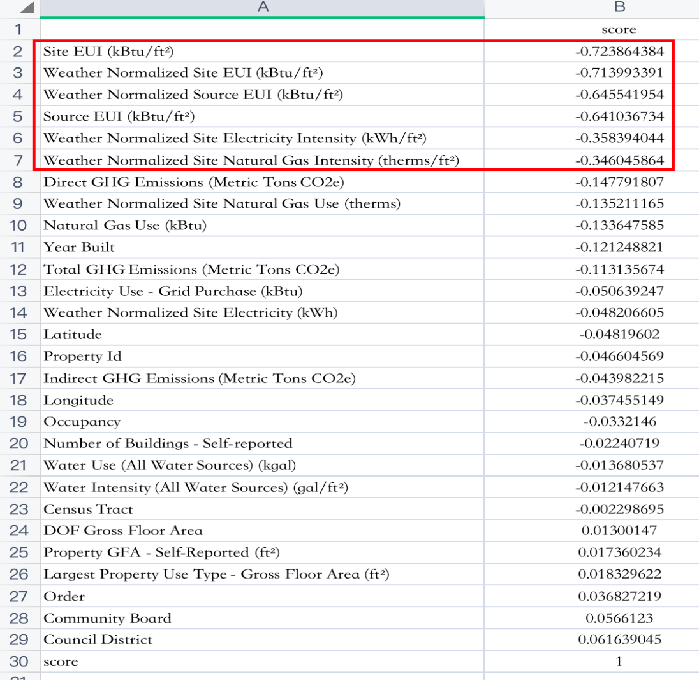
进一步对相关系数数据进行处理来探索x和y之间是否存在线性关系、非线性关系
- 探索特征值x与y
- 方法:是不是存在非线性关系对每一列x特征求平方根和对数, 然后再观察相关系数前后排名变化

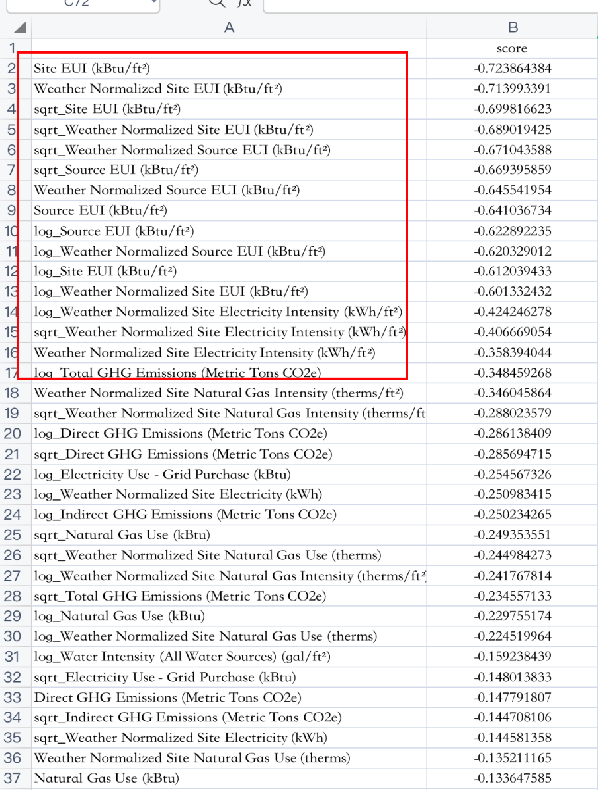
5.4 双变量关系图

python 复制代码

def eda04_计算双变量关系(data, features):
    # 1-1  最大物业特征超过100条的 名称列表 [前面已经写过的代码]
    types = data.dropna(subset=['score'])  # 去除
    types = types['Largest Property Use Type'].value_counts()
    # ['Multifamily Housing', 'Office', 'Hotel', 'Non-Refrigerated Warehouse'] : ['多户住宅'、'办公室'、'酒店'、'非冷藏仓库']
    types = types[types.values > 100].index
    # print('types-->', types)
    # 1-2 features中增加最大物业特征列，使用散点图可视化两个变量的关系并加上颜色分类; 提取building types数据[9461,138] --> [9461,139]
    features['Largest Property Use Type'] = data.dropna(subset=['score'])['Largest Property Use Type']
    # 1-3 提取4大物业的数据 [9461, 139] --> [8979, 139]
    features = features[features['Largest Property Use Type'].isin(types)]
    # 1-4 绘制4大物业与sorce之间的散点图
    # Seaborn绘制散点图 alpha:图形的透明度 s:点的大小 fit_reg:是否画出拟合直线 hue:根据分类 不同颜色显示
    figsize(12, 10)
    sns.lmplot(x='Site EUI (kBtu/ft²)', y='score',
               hue='Largest Property Use Type', 
               data=features,
               scatter_kws={'alpha': 0.8, 's': 60}, 
               fit_reg=False,
               height=15, 
               aspect=1.2) 
    # size:高度 aspect:宽高比
    # 调整坐标轴上的标签和标题
    plt.xlabel('Site EUI', size=28)
    plt.ylabel('Energy Star Score', size=28)
    plt.title('Energy Star Score vs Site EUI', size=36)
    plt.show() 

    # 2 成对关系图 有关画图: 出报告的时画图: 1业务不熟悉想看元素和元素之间的关系画图 2业务熟了意义不大
    # 2-1提取要绘制的特征
    plot_data = features[['score', 'Site EUI (kBtu/ft²)',
                          'Weather Normalized Source EUI (kBtu/ft²)',
                          'log_Total GHG Emissions (Metric Tons CO2e)']]
    # 2-2 将inf替换成nan
    # np.log(0)->-inf np.log(x),x非常大,计算内存溢出->inf
    plot_data = plot_data.replace({np.inf: np.nan, -np.inf: np.nan})
    # 2-3重命名列
    plot_data = plot_data.rename(columns={'Site EUI (kBtu/ft²)': 'Site EUI',
                                          'Weather Normalized Source EUI (kBtu/ft²)': 'Weather Norm EUI',
                                          'log_Total GHG Emissions (Metric Tons CO2e)': 'log GHG Emissions'})
    # 2-4 去掉缺失值
    plot_data = plot_data.dropna()
    def corr_func(x, y, **kwargs):  # 计算相关系数
        r = np.corrcoef(x, y)[0][1] # 根据数据格式把r提取出来 print('\n-->', np.corrcoef(x, y))
        """
        array([[ 1.        , -0.74116006],
       [-0.74116006,  1.        ]])
        """
        # Get Current Axes，获取当前坐标轴， 如果没有会创建新的坐标轴
        ax = plt.gca()  
        # 在图形的指定位置添加文本注释
        # xy：文本注释的位置， x轴位置是 20% 处， y轴位置是 80% 处
        # xycoords：ax.transAxes 坐标系是基于轴的坐标系（轴坐标系），即 xy=(0, 0) 是坐标轴的左下角，xy=(1, 1) 是右上角
        ax.annotate('r={:.2f}'.format(r), # 数据2位小数
                    xy=(.2, .8), xycoords=ax.transAxes, 
                    size=20)
    # 2-5 绘制成对关系图
    # 创建成对关系图对象
    grid = sns.PairGrid(data=plot_data, height=3)
    grid.map_upper(plt.scatter, color='red', alpha=0.6) # 右上绘制散点图
    grid.map_diag(plt.hist, color='red', edgecolor='black') # 对角线绘制直方图
    grid.map_lower(corr_func) # 左下显示相关性绘制density plot
    grid.map_lower(sns.kdeplot, cmap=plt.cm.Reds)
    # 设置标题
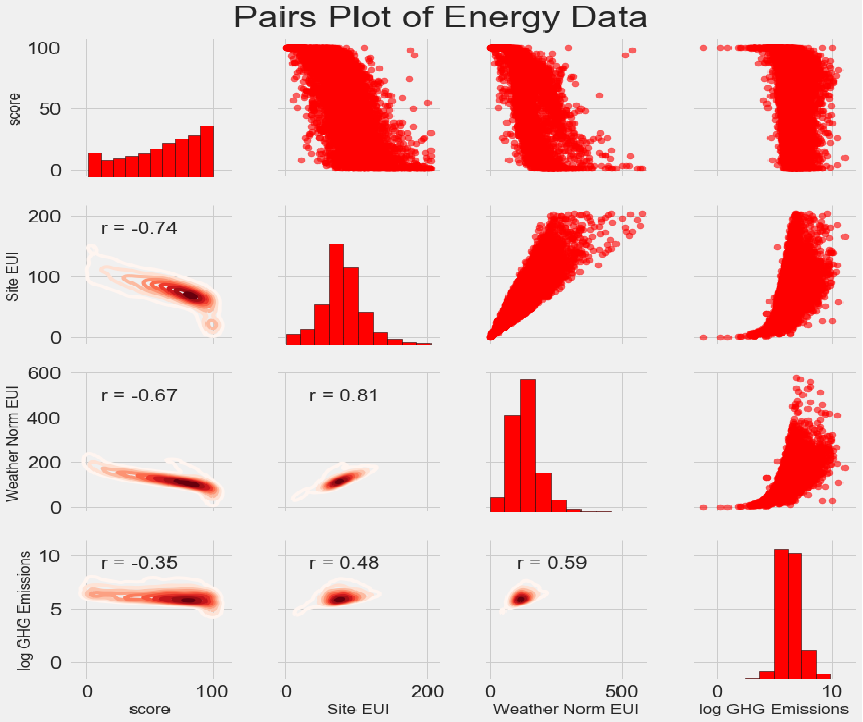
    plt.suptitle('Pairs Plot of Energy Data', size=36, y=1.02)
    plt.show()

使用散点图可视化两个变量的关系并加上颜色分类，更方便的理解业务数据
- 站点 EUI 与分数之间存在明显的负相关关系。这种关系不是完全线性的（看起来相关系数为-0.7，但看起来这个特征对于预测建筑物的得分很重要。
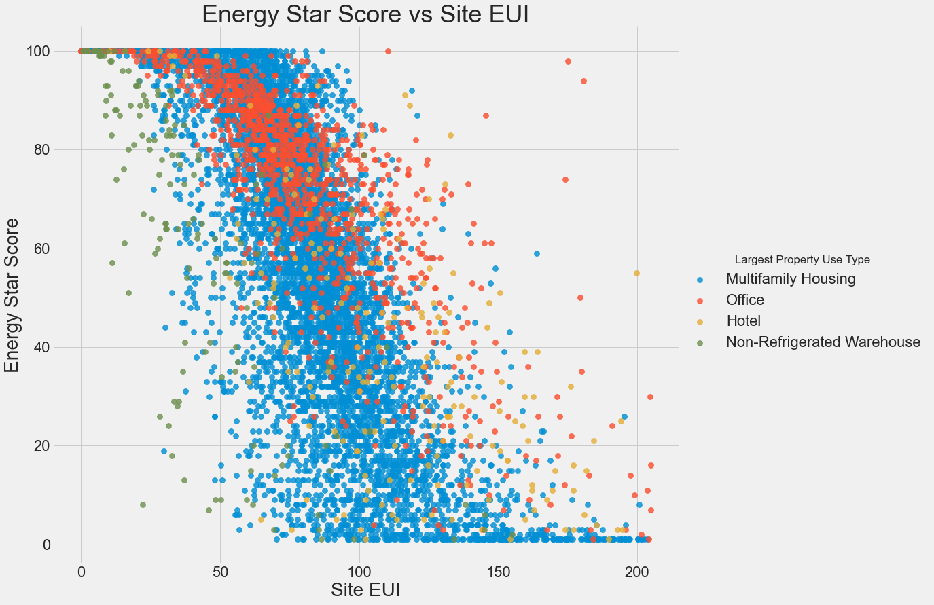
几个不同的变量之间绘制成对关系图，也可更方便的理解业务数据
- 可控制成对关系的显示方式. 使用 seaborn PairGrid 函数；
- 将不同类型的图形映射到网格的三个部分：
  - 上三角显示散点图
  - 对角线显示直方图
  - 下三角显示两个变量之间的相关系数和两个变量的二维核密度估计

5.5 EDA结论

目标值score的分布与建筑类型有很强的相关性
目标值在不同的行政区域也有略微的不同
对特征进行对数变换不会导致特征与分数之间的线性相关性显着增加

6 特征工程

本案例特征选择要做的工作
- 仅选择数值变量和两个分类变量（自治市镇和物业使用类型）
- 对数值变量进行对数变换，对类别型特征进行One-hot编码
- 组合上述特征，讨论共线性（也称为多重共线性），删除
其他特征工程：数据集划分、数据标准按照正常流程

删除共线性特征方法

python 复制代码

def remove_collinear_features(x, threshold):
    y = x['score']   # 在原始数据X中'score'当做y值
    x = x.drop(columns = ['score'])  # 除去标签值以外的当做特征
    # 多长运行，直到相关性小于阈值才稳定结束
    while True:
        # 计算一个矩阵，两两的相关系数
        corr_matrix = x.corr() 
        for i in range(len(corr_matrix)):
            corr_matrix.iloc[i, i] = 0  # 将对角线上的相关系数置为0。避免自己跟自己计算相关系数一定大于阈值
        # 定义待删除的特征
        drop_cols = []
        # col返回的是列名
        for col in corr_matrix.columns:
            if col not in drop_cols:  # A和B比，B和A比的相关系数一样，避免AB全删了
                # 取相关系数的绝对值
                v = np.abs(corr_matrix[col])  # 取的是每一列的相关系数
                # 如果相关系数大于设置的阈值    
                if np.max(v) > threshold:
                    # 取出最大值对应的索引
                    name = v.index[np.argmax(v)]  # 找到最大值的的列名
                    drop_cols.append(name)
         # 列表不为空，就删除，列表为空，符合条件，退出循环           
        if drop_cols:
            # 删除想删除的列
            x = x.drop(columns=drop_cols)
        else:
            break
    # 删除共线性特征后的x增加y标签
    x['score'] = y        
    return x

特征工程方法

python 复制代码

def dm03_特征工程(data):
    # 1准备数据 删除异常值后的data
    # 1-1 复制原始数据features / data.copy()
    features = data.copy()
    # 1-2 选择数值类特征
    numeric_subset = features.select_dtypes('number')
    for col in numeric_subset.columns:
        if col == 'score':
            next
        else:
            numeric_subset['log_' + col] = np.log(numeric_subset[col])
    # 1-3 选中类别型特征
    categorical_subset = features[['Borough', 'Largest Property Use Type']]
    categorical_subset = pd.get_dummies(categorical_subset)
    # 1-4 数值型/类别型特征拼接在一起
    features = pd.concat([numeric_subset, categorical_subset], axis=1)
    print('数值型/类别型特征拼接在一起features.shape-->', features.shape)  # [11319, 110]
    # 1-5 移除相关特征- 线性相关性画图 - 小实验
    # plot_data = data[['Weather Normalized Site EUI (kBtu/ft²)', 'Site EUI (kBtu/ft²)']].dropna()
    # print(plot_data.corr())
    # plt.plot(plot_data['Site EUI (kBtu/ft²)'], plot_data['Weather Normalized Site EUI (kBtu/ft²)'], 'bo')
    # plt.xlabel('Site EUI')
    # plt.ylabel('Weather Norm EUI')
    # plt.title('Weather Norm EUI vs Site EUI')
    # plt.show() 
    
    # 2-1根据阈值删除强相关的特征 remove_collinear_features(features, 0.6)
    features = remove_collinear_features(features, 0.6)
    # 2-2 对特征值nan列数据进行处理 features.dropna(axis=1, how='all')
    # Longitude列的值都小于0, 进行log计算时都为nan值
    features = features.dropna(axis=1, how='all')
    print('features.shape-->', features.shape)
    # 2-3 去掉目标值为np.nan的数据 score/ features[features['score'].notnull()]
    score = features[features['score'].notnull()]
    print('score.shape-->', score.shape)
    # 3 训练集和测试集划分
    # 3-1 构建特征与目标 features,targets /score.drop(columns='score') /targets = pd.DataFrame(score['score'])
    features = score.drop(columns='score')
    targets = pd.DataFrame(score['score'])
    # 3-2 替换inf和-inf为nan / features.replace({np.inf: np.nan, -np.inf: np.nan})
    # np.log(0)->-inf np.log(x),x非常大,计算内存溢出->inf
    features = features.replace({np.inf: np.nan, -np.inf: np.nan})
    # 3-3 训练集测试集划分
    X, X_test, y, y_test = train_test_split(features, targets, test_size=0.3, random_state=42)
    print('X.shape-->', X.shape)
    print('X_test.shape-->', X_test.shape)
    print('y.shape-->', y.shape)
    print('y_test.shape-->', y_test.shape)

    # 4 保存到文件 X,training_features.csv /X_test,testing_features.csv /y,training_labels.csv/y_test/testing_labels.csv
    X.to_csv('feature/training_features.csv', index=False)
    X_test.to_csv('feature/testing_features.csv', index=False)
    y.to_csv('feature/training_labels.csv', index=False)
    y_test.to_csv('feature/testing_labels.csv', index=False)
    return X, X_test, y, y_test

建立baseline模型

训练集上预测值的平均值作为基础指标
基础指标与测试集的目标值求MAE

python 复制代码

def dm03_特征工程(data):
    ...
    # 5 建立baseline模型
    # 训练集上的预测值的平均值作为baseline指标 baseline_guess = np.median(y)
    # 计算MAE值 mae(y_test, baseline_guess) / def mae(y_true, y_pred): return np.mean(abs(y_true - y_pred))
    def mae(y_true, y_pred):
        return np.mean(abs(y_true - y_pred))

    baseline_guess = np.median(y)  # y的中位数作为baseline_guess指标 - 训练集/测试集上预测值的平均值
    print('baseline guess 预测的score为 of %0.2f' % baseline_guess)
    print("Baseline 在测试集上的表现: MAE = %0.4f" % mae(y_test, baseline_guess))

7 模型训练和参数调优

7.1 导入工具包

python 复制代码

import pandas as pd
import numpy as np
import warnings
import matplotlib.pyplot as plt #数据可视化
from IPython.core.pylabtools import figsize
import seaborn as sns   # Seaborn 可视化
# 特征值标准化和缺失值填充
from sklearn.preprocessing import MinMaxScaler
from sklearn.impute import SimpleImputer
# 机器学习模型
from sklearn.linear_model import LinearRegression
from sklearn.ensemble import RandomForestRegressor, GradientBoostingRegressor
from sklearn.neighbors import KNeighborsRegressor
# 参数调整
from sklearn.model_selection import RandomizedSearchCV, GridSearchCV

# %matplotlib inline
warnings.filterwarnings('ignore')
# pd.set_option('display.max_columns', 60)
# 设置默认字体
plt.rcParams['font.size'] = 24
sns.set(font_scale=2)

7.2 缺失值填充和数据标准化

本案例缺失值填充
- 采用中位值填充缺失值；填充方法可以根据业务要求采用不同的方案
- 核心代码 imputer = SimpleImputer(strategy='median')
本案例数据标准化
- 采用归一化的方法
- 核心代码 scaler = MinMaxScaler(feature_range=(0, 1))

python 复制代码

def dm01_数据填充特征归一化():
    # 1 根据文件读数据到内存
    train_features = pd.read_csv('feature/training_features.csv')
    test_features = pd.read_csv('feature/testing_features.csv')
    train_labels = pd.read_csv('feature/training_labels.csv')
    test_labels = pd.read_csv('feature/testing_labels.csv')
    # 显示数据形状
    print('Training Feature Size:', train_features.shape)
    print('Testing Feature Size:', test_features.shape)
    print('Training Labels Size:', train_labels.shape)
    print('Testing Labels Size:', test_labels.shape)
    
    # 2 缺失值填充 - 策略使用中位数去填充缺失值
    # 2-1 实例化并fit中位数 imputer /SimpleImputer(strategy='median') /.fit(train_features)
    imputer = SimpleImputer(strategy='median')
    imputer.fit(train_features)
    # 2-2 使用中位数来填充数据得X X_test/ imputer.transform(train_features) imputer.transform(test_features)
    X = imputer.transform(train_features)
    X_test = imputer.transform(test_features)
    # 2-3 确认是否有缺失值 np.isnan(X) / Xtest
    print('确认X是否还有缺失值:', np.sum(np.isnan(X)))
    print('确认X_test是否还有缺失值:', np.sum(np.isnan(X_test)))
    
    # 3 数据归一化 MinMaxScaler(feature_range=(0, 1))
    # 3-1 实例化scaler, 训练fit
    # 3-2 对X X_test进行归一化 scaler.transform(X) /X_test
    scaler = MinMaxScaler(feature_range=(0, 1))
    scaler.fit(X)
    X = scaler.transform(X)
    X_test = scaler.transform(X_test) 
    
    # 4 对标签值进行形状调形 train_labels(6622,1)->(6622,) test_labels(2839,1)->(2839,)
    y = train_labels.values.reshape(-1,)
    y_test = test_labels.values.reshape(-1,)
    
    # 5 返回处理好的数据
    # print(X.shape, X_test.shape, y.shape, y_test.shape)
    return X, X_test, y, y_test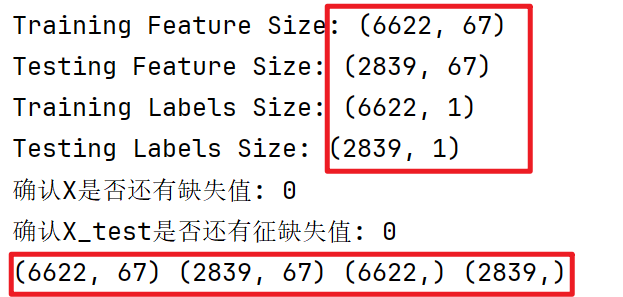

7.3 模型训练

本案例模型选中采用的方法如下
- 测试4个不同模型在当前问题上的表现
  - LR模型、随机森林模型、GBDT模型、KNN模型
- 先不做参数调整根据模型的表现，再选择最优模型做参数调整

python 复制代码

# 在这里的损失函数是MAE ，abs()是绝对值
def mae(y_true, y_pred):
    return np.mean(abs(y_true - y_pred))


# 制作一个模型 ，训练模型和在验证集上验证模型的参数
def fit_and_evaluate(X, X_test, y, y_test, model):
    # 训练模型
    model.fit(X, y)
    # 训练模型开始在测试数据上训练
    model_pred = model.predict(X_test)
    model_mae = mae(y_test, model_pred)
    return model_mae


def dm02_modeltrain(X, X_test, y, y_test):
    # 1 训练LR模型 lr/ LinearRegression()
    lr = LinearRegression()
    lr_mae = fit_and_evaluate(X, X_test, y, y_test, lr)
    print('lr_mae-->', lr_mae)
    # 2 训练随机森林模型 random_forest/ RandomForestRegressor(random_state=60)
    random_forest = RandomForestRegressor(random_state=60)
    random_forest_mae = fit_and_evaluate(X, X_test, y, y_test, random_forest)
    print('random_forest_mae-->', random_forest_mae)
    # 3 训练GBDT模型 gradient_boosted/ GradientBoostingRegressor(random_state=60)
    gradient_boosted = GradientBoostingRegressor(random_state=60)
    gradient_boosted_mae = fit_and_evaluate(X, X_test, y, y_test, gradient_boosted)
    print('gradient_boosted_mae-->', gradient_boosted_mae)
    # 4 训练KNN模型 knn/ KNeighborsRegressor(n_neighbors=10)
    knn = KNeighborsRegressor(n_neighbors=10)
    knn_mae = fit_and_evaluate(X, X_test, y, y_test, knn)
    print('knn_mae-->', knn_mae)
    # 5 绘图比较mae值
    # 5-1 创建DataFrame来保存结果
    model_comparison = pd.DataFrame({'model': ['Linear Regression',  'Random Forest', 'Gradient Boosted','K-Nearest Neighbors'],'mae': [lr_mae,  random_forest_mae, gradient_boosted_mae, knn_mae]})
    # 5-2 # 绘制横向柱状图
    figsize(8, 6)
    plt.style.use('fivethirtyeight')
    model_comparison.sort_values('mae', ascending=False).plot(x='model', y='mae', kind='barh', color='red', edgecolor='black')
    # 5-3 图片格式调整 添加坐标轴的标签以及标题
    plt.ylabel('')
    plt.yticks(size=14)
    plt.xlabel('Mean Absolute Error')
    plt.xticks(size=14)
    plt.title('Model Comparison on Test MAE', size=20)
    plt.show()

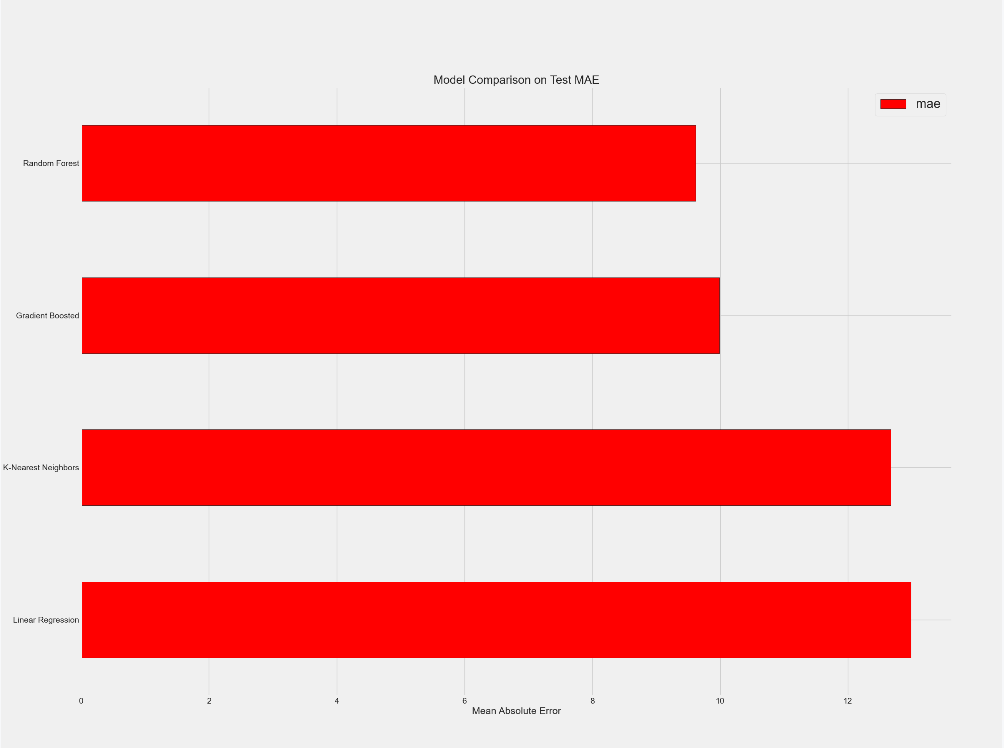
从图运行结果分析：集成学习模型的效果最好。后续的超参数调整主要针对两个集成学习模型。

7.4 参数调优

模型调优意味着为特定问题找到最佳的超参数组合
- 通过训练更复杂的模型可以解决欠拟合问题
  - 比如：随机森林中使用更多树，欠拟合的模型具有高偏差
- 通过限制模型的复杂性和应用正则化可以纠正过拟合
  - 味着降低多项式回归的高次项，限制树的深度。过拟合的模型具有高方差
- 欠拟合和过拟合都会导致测试集的泛化性能差
- 调整模型超参数可控制模型中欠拟合与过拟合的平衡
本案例模型参数调优粗调和精调想结合
- RandomizedSearchCV为通过随机参数组合提供粗调最佳超参数
  - 随机搜索是SKlearn提供的超参数调优方法
  - 优点速度快：RandomizedSearchCV是缩小要尝试的可能超参数的好方法
  - 我们不知道哪种组合效果最好，通过随机搜索我们可以缩小超参数的选择范围
- GridSearchCV为模型提供精调最佳超参数
- 全面细致搜索参数组合
- 缺点：速度慢

粗调代码

python 复制代码

def dm03_modelparam(X, y):
    # 1 设置超参数
    # 1-1  准备参数 n_estimators max_depth min_samples_leaf min_samples_split max_features
    n_estimators = [30, 60, 90, 100, 150]  # 有多少棵树 
    max_depth = [1, 2, 3, 4, 5]  # 树的最大深度
    min_samples_leaf = [2, 4, 6, 8]  # 每个叶子节点的最少样本数量
    min_samples_split = [2, 4, 6, 10]  # 节点分裂需满足的最少样本数量
    max_features = [1.0, 'sqrt', 'log2', None]  # 建树使用的最大特征
    # 1-2 定义要搜索的参数
    hyperparameter_grid = {'n_estimators': n_estimators,
        'max_depth': max_depth,
        'min_samples_leaf': min_samples_leaf,
        'min_samples_split': min_samples_split,
        'max_features': max_features}
    # 2 实例化模型 GradientBoostingRegressor
    model = GradientBoostingRegressor(random_state=42)
    # 3 随机超参数RandomizedSearchCV() estimator, param_distributions, cv=4, 	# n_iter=25，随机选取25个超参数组合进行实验
    # scoring='neg_mean_absolute_error', 负平均绝对误差, sklearn评分越大模型越好, MAE越小表示模型越好
    # n_jobs=-1, 使用所有可用的 CPU 核心进行计算
    # verbose=1, 显示每次迭代的信息
    # return_train_score=True，在返回的结果中包含训练集的评分。这样可以帮助你分析模型是否存在过拟合问题。
    random_cv = RandomizedSearchCV(estimator=model,
                                   param_distributions=hyperparameter_grid,
                                   cv=4, n_iter=25,
                                   scoring='neg_mean_absolute_error',
                                   n_jobs=-1, verbose=1,
                                   return_train_score=True,
                                   random_state=42)
    random_cv.fit(X, y)
    
    # 4 查看结果
    # 4-1 查看交叉验证结果 random_cv.cv_results_是一个字典转pd.DataFrame(random_cv.cv_results_).to_csv
    # random_results = pd.DataFrame(random_cv.cv_results_).sort_values('mean_test_score', ascending=False)
    # print('random_results.head(10)-->\n', random_results.head(10))
    pd.DataFrame(random_cv.cv_results_).to_csv('./cv_results.csv')
    # 4-2 查看最佳模型参数 random_cv.best_estimator_, random_cv.best_score_
    print('random_cv.best_estimator_-->\n', random_cv.best_estimator_)
    print('random_cv.best_score_-->', random_cv.best_score_)

细调代码

python 复制代码

def dm04_modelparam(X, X_test, y, y_test):
    # 1 对n_estimator参数进行精调
    # trees_grid = {'n_estimators': [100, 150, 200, 250, 300, 350, 400, 450, 500, 550, 600, 650, 700, 750]}
    trees_grid = {'n_estimators': [100, 150, 200, 250, 300, 350, 400]}
    
    # 2 用粗调模型参数实例化GradientBoostingRegressor max_depth=5 min_samples_leaf=4  min_samples_split=2 max_features=None
    model = GradientBoostingRegressor(max_depth=5,
                                      min_samples_leaf=4,
                                      min_samples_split=2,
                                      max_features=None)
    
    # 3 使用grid_search / GridSearchCV()实例化, 并fit(X, y)
    # 参数:estimator=, param_grid=,cv=4,scoring='neg_mean_absolute_error', n_jobs=-1, return_train_score=True,verbose=1,
    grid_cv = GridSearchCV(estimator=model, param_grid=trees_grid, cv=4,
                               scoring='neg_mean_absolute_error', verbose=1,
                               n_jobs=-1, return_train_score=True)
    grid_cv.fit(X, y)
    
    # 4 训练集误差, 测试集误差, 随树数量变化趋势图
    # 重点观察: results['param_n_estimators']; results['mean_test_score']; results['mean_train_score']
    results = pd.DataFrame(grid_cv.cv_results_)
    figsize(8, 8)
    plt.style.use('fivethirtyeight')
    plt.plot(results['param_n_estimators'], -1 * results['mean_test_score'], label='Testing Error')
    plt.plot(results['param_n_estimators'], -1 * results['mean_train_score'], label='Training Error')
    plt.xlabel('Number of Trees')
    plt.ylabel('Mean Abosolute Error')
    plt.legend()
    plt.title('Performance vs Number of Trees')
    plt.show()
    
    # 5 比较默认模型和最佳模型在测试集的MAE表现
    # 5-1 实例化默认模型 default_model / GradientBoostingRegressor()
    # 实例化最佳模型 final_model/ grid_search.best_estimator_
    default_model = GradientBoostingRegressor(random_state=60)
    final_model = grid_cv.best_estimator_
    print('final_model-->\n', final_model)
    # 5-2 模型训练和预测default_pred,final_pred / fit(X, y),predict(X_test)
    default_model.fit(X, y)
    final_model.fit(X, y)
    default_pred = default_model.predict(X_test)
    final_pred = final_model.predict(X_test)
    # 5-3 计算 mae(y_test, default_pred) /final_pred
    # 精调模型MAE效果会更好
    print('默认模型test set: MAE = %0.4f.' % mae(y_test, default_pred))
    print('精调模型test set: MAE = %0.4f.' % mae(y_test, final_pred))
    
    # 6 绘制真实值与预测值的Kde图
    figsize(8, 8)
    sns.kdeplot(final_pred, label='Predictions')
    sns.kdeplot(y_test, label='Values')
    plt.xlabel('Energy Star Score')
    plt.ylabel('Density')
    plt.title('Test Values and Predictions')   
    plt.show()
    
    # 7 绘制预测误差分布图, 如果残差符合正态分布, 说明模型效果不错
    figsize(8, 8)
    residuals = final_pred - y_test # 计算预测误差
    plt.hist(residuals, color='red', bins=20, edgecolor='black') # 绘制残差的直方图
    plt.xlabel('Error')
    plt.ylabel('Count')
    plt.title('Distribution of Residuals')
    plt.show()

模型会有过拟合现象

随着estimator数量的增加，过度拟合程度也会增加

随着estimator数量的增加，测试和训练误差都会减少

但训练误差会更快地减少

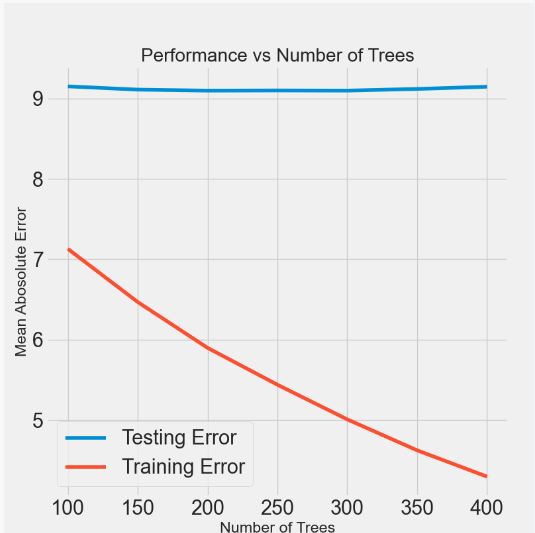
精调模型MAE效果比默认模型要好

测试数据上评估最终模型

真实值与预测值的Kde图：从分布形状上来看整体误差不大, 但是在预测极值上能力欠佳

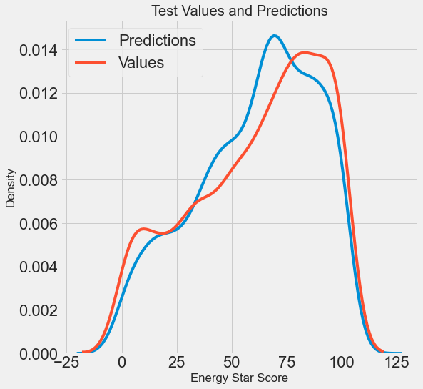
预测误差柱状图：从残差接近正态分布

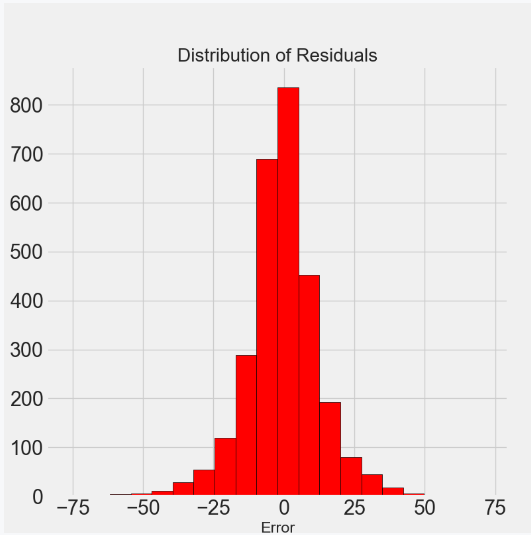
8 模型特征解读

缺失值填充和数据标准化代码

这个代码和以前的函数非常类似，只不过增加了返回值feature_columns，因要探索特征重要性，所以返回此项

python 复制代码

def dm01_数据填充特征归一化():
    # 1 根据文件读数据到内存
    train_features = pd.read_csv('feature/training_features.csv')
    test_features = pd.read_csv('feature/testing_features.csv')
    train_labels = pd.read_csv('feature/training_labels.csv')
    test_labels = pd.read_csv('feature/testing_labels.csv')
    # 显示数据形状
    print('Training Feature Size: ', train_features.shape)
    print('Testing Feature Size:  ', test_features.shape)
    print('Training Labels Size:  ', train_labels.shape)
    print('Testing Labels Size:   ', test_labels.shape)
    # 2 缺失值填充 - 策略使用中位数去填充缺失值
    # 2-1 实例化并fit中位数 imputer /SimpleImputer(strategy='median') /.fit(train_features)
    imputer = SimpleImputer(strategy='median')
    imputer.fit(train_features)
    # 2-2 使用中位数来填充数据得X X_test/ imputer.transform(train_features) imputer.transform(test_features)
    X = imputer.transform(train_features)
    X_test = imputer.transform(test_features)
    # 2-3 确认是否有缺失值 np.isnan(X) / Xtest
    print('确认X是否还有缺失值:', np.sum(np.isnan(X)))
    print('确认X_test是否还有征缺失值:', np.sum(np.isnan(X_test)))
    # 3 数据归一化 MinMaxScaler(feature_range=(0, 1))
    # 3-1 实例化scaler, 训练fit
    # 3-2 对X X_test进行归一化 scaler.transform(X) /X_test
    scaler = MinMaxScaler(feature_range=(0, 1))
    scaler.fit(X)
    X = scaler.transform(X)
    X_test = scaler.transform(X_test) 
    # 4 对标签值进行形状调形 train_labels(6622,1)->(6622,) test_labels(2839,1)->(2839,)
    y = np.array(train_labels).reshape((-1,))
    y_test = np.array(test_labels).reshape((-1,))
    # 5 返回处理好的数据 返回特征列
    # print(X.shape, X_test.shape, y.shape, y_test.shape)
    feature_columns = train_features.columns
    return X, X_test, y, y_test, feature_columns

获取模型特征代码

python 复制代码

def dm02_modelfeature(X, X_test, y, y_test, feature_columns):
    # 1 训练最佳模型
    # 1-1 实例化gdbmodel GradientBoostingRegressor
    # 参数max_depth=5, max_features=None,  min_samples_leaf=4, min_samples_split=2, n_estimators=200, random_state=42
    model = GradientBoostingRegressor(max_depth=5, max_features=None,min_samples_leaf=4, min_samples_split=2, n_estimators=200, random_state=42)
    # 1-2 训练fit(X, y)模型
    model.fit(X, y)
    # 1-3 模型测试集预测 mae评估
    model_pred = model.predict(X_test)
    print(mae(y_test, model_pred))
    
    # 2 模型特征重要性查看
    # 2-1 feature_results 转成DataFrame 参数{'feature': list(feature_columns), 'importance': model.feature_importances_}
    feature_results = pd.DataFrame({'feature': list(feature_columns), 'importance': model.feature_importances_})
    # 2-2 特征重要性排序 显示前十个最重要的特征
    # 重设索引drop=True,删除原来的索引值 .sort_values('importance', ascending=False).reset_index(drop=True)
    feature_results = feature_results.sort_values('importance', ascending=False).reset_index(drop=True)
    print('最重要的10个特征-->\n', feature_results.head(10))
    
    # 3 绘图横向条形图, 显示前十个重要特征
    # figsize(12, 10)
    # plt.style.use('fivethirtyeight')
    # feature_results.loc[:9, :].plot(x='feature', y='importance', edgecolor='k',  kind='barh', color='blue')
    # plt.xlabel('Relative Importance', size=20)
    # plt.ylabel('')
    # plt.title('Feature Importances from Random Forest', size=30)
    # plt.show()   
    
    # 4 大多数特征重要程度都很低, 尝试去掉一部分特征, 看看模型效果是否有变化 准备特征前10名的数据
    # 4-1 取出前10名特征 most_important_features / feature_results['feature'][:10]
    most_important_features = feature_results['feature'][:10]
    # 4-2 找到最重要的特征对应的列indices / [list(feature_columns).index(x) for x in most_important_features]
    indices = [list(feature_columns).index(x) for x in most_important_features]
    # 4-3 准备新的数据X_reduced, X_test_reduced / X[:, indices], X_test[:, indices]
    X_reduced = X[:, indices]
    X_test_reduced = X_test[:, indices]
    print('X_reduced.shape-->', X_reduced.shape)
    print('X_test_reduced.shape-->', X_test_reduced.shape)
    
    # 5 线性回归训模型训练和预测,MAE评估
    # 5-1 训练线性回归 LinearRegression()
    # 5-2 使用60个特征列的数据训练模型并预测lr_full_pred  / lr.fit(X, y), lr.predict(X_test)
    # 5-3 使用10个特征列的数据训练模型并预测lr_reduced_pred / lr.fit(X_reduced, y), lr.predict(X_test_reduced)
    # 5-4 对比mae评估 mae(y_test, lr_full_pred) / mae(y_test, lr_reduced_pred)
    lr = LinearRegression()
    lr.fit(X, y)
    lr_full_pred = lr.predict(X_test)
    lr.fit(X_reduced, y)
    lr_reduced_pred = lr.predict(X_test_reduced)
    print('线性回归训练全部特征的mae-->', mae(y_test, lr_full_pred))
    print('线性回归训练10特征的mae-->', mae(y_test, lr_reduced_pred))
    
    # 6 gbdt模型训练和预测,MAE评估
    # 6-1 实例化 GradientBoostingRegressor()
    # 参数 max_depth=5, max_features=None,min_samples_leaf=4, min_samples_split=2, n_estimators=200, random_state=42
    model_reduced = GradientBoostingRegressor(max_depth=5, max_features=None, min_samples_leaf=4, min_samples_split=2, n_estimators=200, random_state=42)
    # 6-2 训练模型model_reduced / fit(X_reduced, y)
    model_reduced.fit(X_reduced, y)
    # 6-3 模型预测 model_reduced_pred / predict(X_test_reduced) 模型评估 mae(y_test, model_reduced_pred)  
    model_reduced_pred = model_reduced.predict(X_test_reduced)
    print('gbdt训练10个特征的mae-->', mae(y_test, model_reduced_pred))

从图中分析：Site EUI (kBtu/ft²),log_Weather Normalized Site Electricity Intensity (kWh/ft²) 这两个特征, 重要性比较显著, 其余特征均不是很重要

近40个特征得分接近0

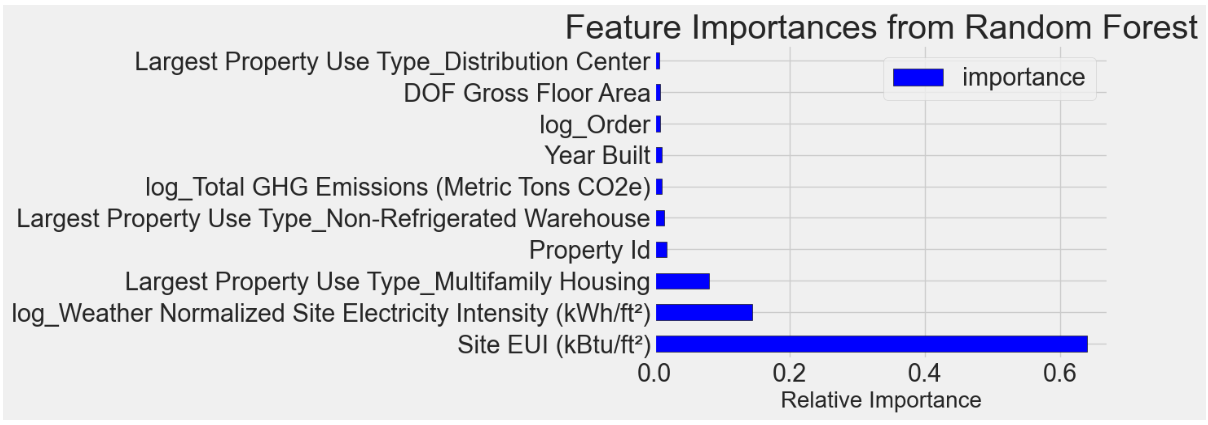
随着特征的减少模型结果稍差，我们将保留最终模型的所有特征

尝试减少特征数量，是因为我们的目标是在保证性能的前提下构建最简单的模型

简单模型：模型特征较少，训练速度更快，并且可解释性更强

', mae(y_test, lr_reduced_pred))

复制代码

  # 6 gbdt模型训练和预测,MAE评估
  # 6-1 实例化 GradientBoostingRegressor()
  # 参数 max_depth=5, max_features=None,min_samples_leaf=4, min_samples_split=2, n_estimators=200, random_state=42
  model_reduced = GradientBoostingRegressor(max_depth=5, max_features=None, min_samples_leaf=4, min_samples_split=2, n_estimators=200, random_state=42)
  # 6-2 训练模型model_reduced / fit(X_reduced, y)
  model_reduced.fit(X_reduced, y)
  # 6-3 模型预测 model_reduced_pred / predict(X_test_reduced) 模型评估 mae(y_test, model_reduced_pred)  
  model_reduced_pred = model_reduced.predict(X_test_reduced)
  print('gbdt训练10个特征的mae-->', mae(y_test, model_reduced_pred))


从图中分析：Site EUI (kBtu/ft²),log_Weather Normalized Site Electricity Intensity (kWh/ft²) 这两个特征, 重要性比较显著, 其余特征均不是很重要

近40个特征得分接近0

<img src="https://i-blog.csdnimg.cn/img_convert/387fbf32b76c80d65054b60a87aca835.png"  style="zoom:70%;" />

随着特征的减少模型结果稍差，我们将保留最终模型的所有特征

尝试减少特征数量，是因为我们的目标是在保证性能的前提下构建最简单的模型

简单模型：模型特征较少，训练速度更快，并且可解释性更强

<img src="https://ltwhahaha.oss-cn-beijing.aliyuncs.com/%E7%9B%AE%E5%BD%951/1736520074353.png"  style="zoom:70%;" />