排序算法-选择排序

排序算法（sorting algorithm）用于对一组数据按照特定顺序进行排列。排序算法有着广泛的应用，因为有序 数据通常能够被更高效地查找、分析和处理。

选择排序

选择排序（selection sort）的工作原理非常简单：开启一个循环，每轮从未排序区间选择最小的元素，将其放 到已排序区间的末尾。

步骤

1. 初始状态下，所有元素未排序，即未排序（索引）区间为 0, 𝑛 − 1 。

2. 选取区间 0, 𝑛 − 1 中的最小元素，将其与索引 0 处的元素交换。完成后，数组前 1 个元素已排序。

3. 选取区间 1, 𝑛 − 1 中的最小元素，将其与索引 1 处的元素交换。完成后，数组前 2 个元素已排序。

4.以此类推。经过 n-1 轮选择与交换后，数组前 n-1 个元素已排序。

5.仅剩的一个元素必定是最大元素，无须排序，因此数组排序完成。

演示流程

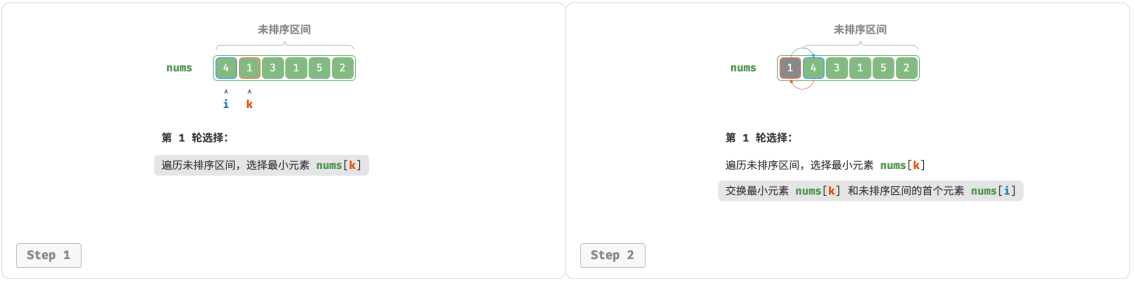
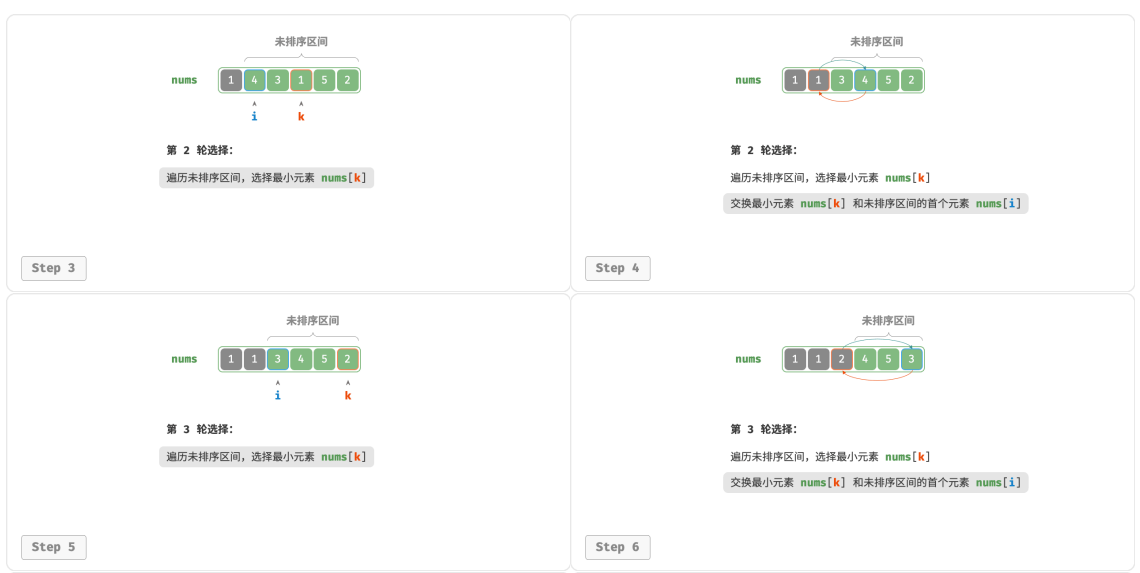
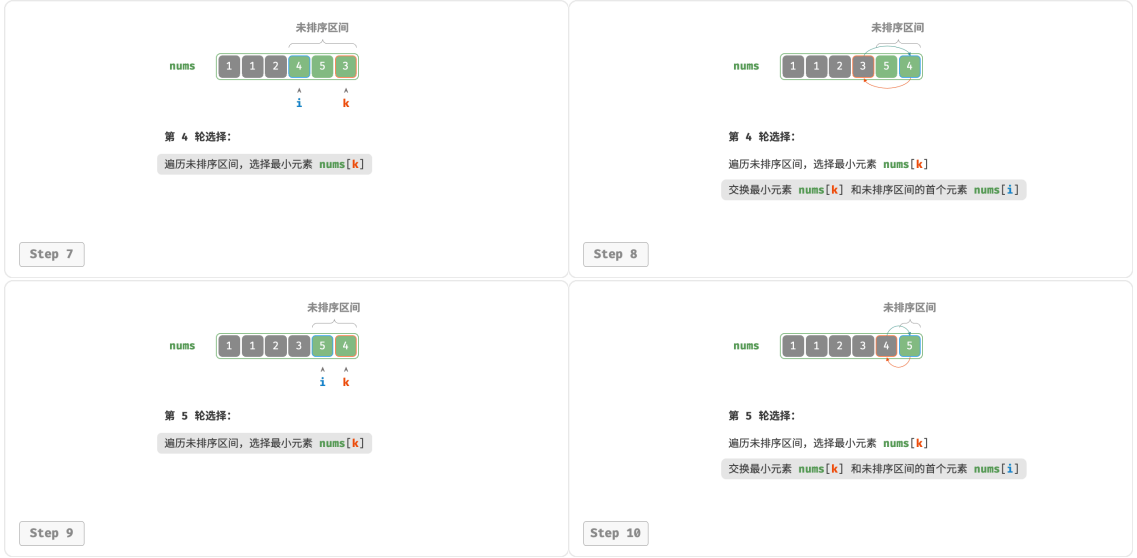
python代码实现

def selection_sort(nums: list[int]):
    """选择排序"""
    n = len(nums)
    # 外循环：未排序区间为 [i, n-1]
    for i in range(n - 1):
        # 内循环：找到未排序区间内的最小元素
        k = i
        for j in range(i + 1, n):
            if nums[j] < nums[k]:
                k = j  # 记录最小元素的索引
        # 将该最小元素与未排序区间的首个元素交换
        nums[i], nums[k] = nums[k], nums[i]

算法特性

• 时间复杂度为 、非自适应排序 ：外循环共 n-1轮，第一轮的未排序区间长度为 n ，最后一轮的未排序区间长度为 2，即各轮外循环分别包含n、n-1、...、3、 2轮内循环，求和为 。
• 空间复杂度为 、原地排序：指针 i 和 j 使用常数大小的额外空间。
• 非稳定排序 ：元素 nums[i] 有可能被交换至与其相等的元素的右边，导致两者的相对顺序发生改变。