在计算机组成原理的学习中,移位运算 是一个看似简单却内涵丰富的操作。它不仅是实现乘除法的基础,更是理解数据表示、硬件设计与数值精度的关键窗口。很多同学初学时觉得"不就是左右移动几位嘛",但一旦深入定点数的三种编码(原码、反码、补码),就会发现:不同的编码方式,移位时的"补位规则"竟大相径庭。
更令人困惑的是,除了"算术移位",还有"逻辑移位"和"循环移位"------它们各自适用什么场景?为什么补码右移要补 1 而不是 0?RGB 颜色值拼接为何要用逻辑移位?带进位的循环移位又是什么?
本文将带你从十进制直觉出发,层层递进到二进制定点数的三种移位方式,结合具体数值示例、硬件实现逻辑与实际应用场景
一、移位的本质:改变位权,等效乘除
1.1 从十进制说起:小数点移动的魔法
我们从小就知道:
- 将 985.211 的小数点右移一位 → 9852.11 ,相当于 ×10
- 右移两位 → 98521.1 ,相当于 ×100 = ×10²
- 小数点左移一位 → 98.5211 ,相当于 ÷10
- 左移两位 → 9.85211 ,相当于 ÷100 = ÷10²
为什么? 因为每个数码位的"权重"是以小数点为基准的。移动小数点,就改变了每一位的实际贡献值。
例如,原数中 "9" 在百位(权重 10²),右移后变成千位(权重 10³),数值扩大 10 倍。

1.2 二进制的困境与突破
但在定点数 中,小数点位置是固定的(如定点整数的小数点在最低位右侧,定点小数在最高位左侧)。我们无法像十进制那样"移动小数点"。
怎么办?山不转,水转 ------既然不能动小数点,那就移动数值本身!
通过整体左移或右移数值位 ,改变每一位与小数点的相对位置,从而改变其位权,达到等效乘除的效果。
- 左移 1 位 → 每一位权重 ×2 → 整体 ×2
- 右移 1 位 → 每一位权重 ÷2 → 整体 ÷2
这就是算术移位的核心思想。
🔑 关键结论 :
对二进制定点数进行算术移位,左移等效于乘以 2,右移等效于除以 2。
但问题来了:移出去的位怎么办?空出来的位又该填什么?
答案取决于数的编码方式------原码、反码还是补码。
二、算术移位:符号敏感的精密操作
算术移位的核心要求是:保持数值的符号不变,并尽可能精确地实现乘除效果。因此,补位策略必须考虑符号位。
2.1 原码的算术移位:符号位不动,数值位移
原码表示中,最高位是符号位(0 正,1 负),其余是数值位。
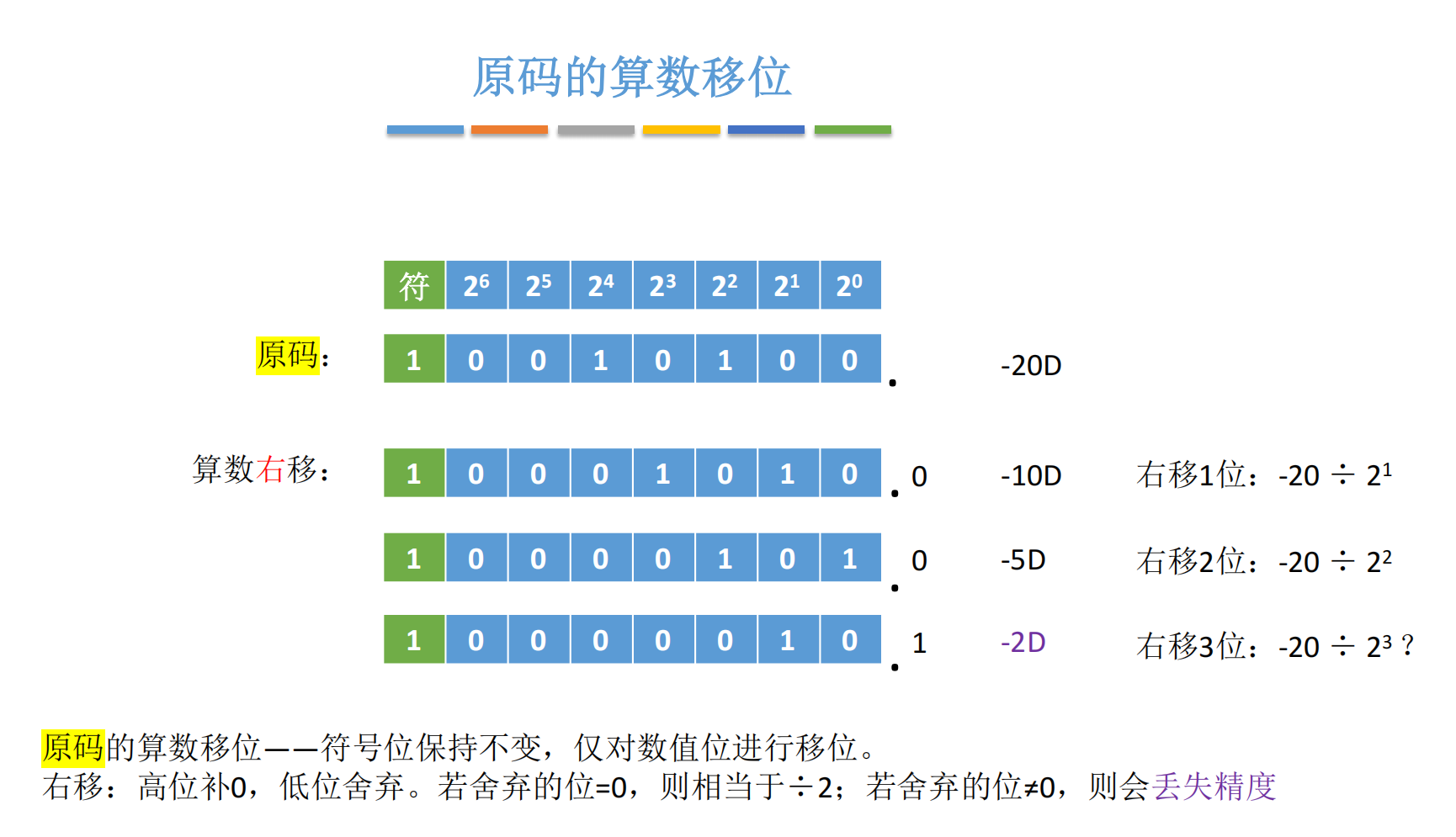
(1)算术右移(÷2)
- 规则 :符号位不变,数值位右移 ,高位补 0 ,低位舍弃
- 效果 :
- 若舍弃位为 0 → 精确 ÷2
- 若舍弃位为 1 → 丢失精度
示例 :−20-20−20 的 8 位原码为 10010100
- 右移 1 位 →
10001010= −10-10−10 ✅(精确) - 再右移 1 位 →
10000101= −5-5−5 ✅(精确) - 再右移 1 位 →
10000010= −2-2−2 ❌(应为 −2.5-2.5−2.5,但舍弃了最低位的 1,丢失 2−12^{-1}2−1 精度)
⚠️ 注意 :原码负数右移时,高位补 0 是因为数值位本身是正的,只是加了符号。
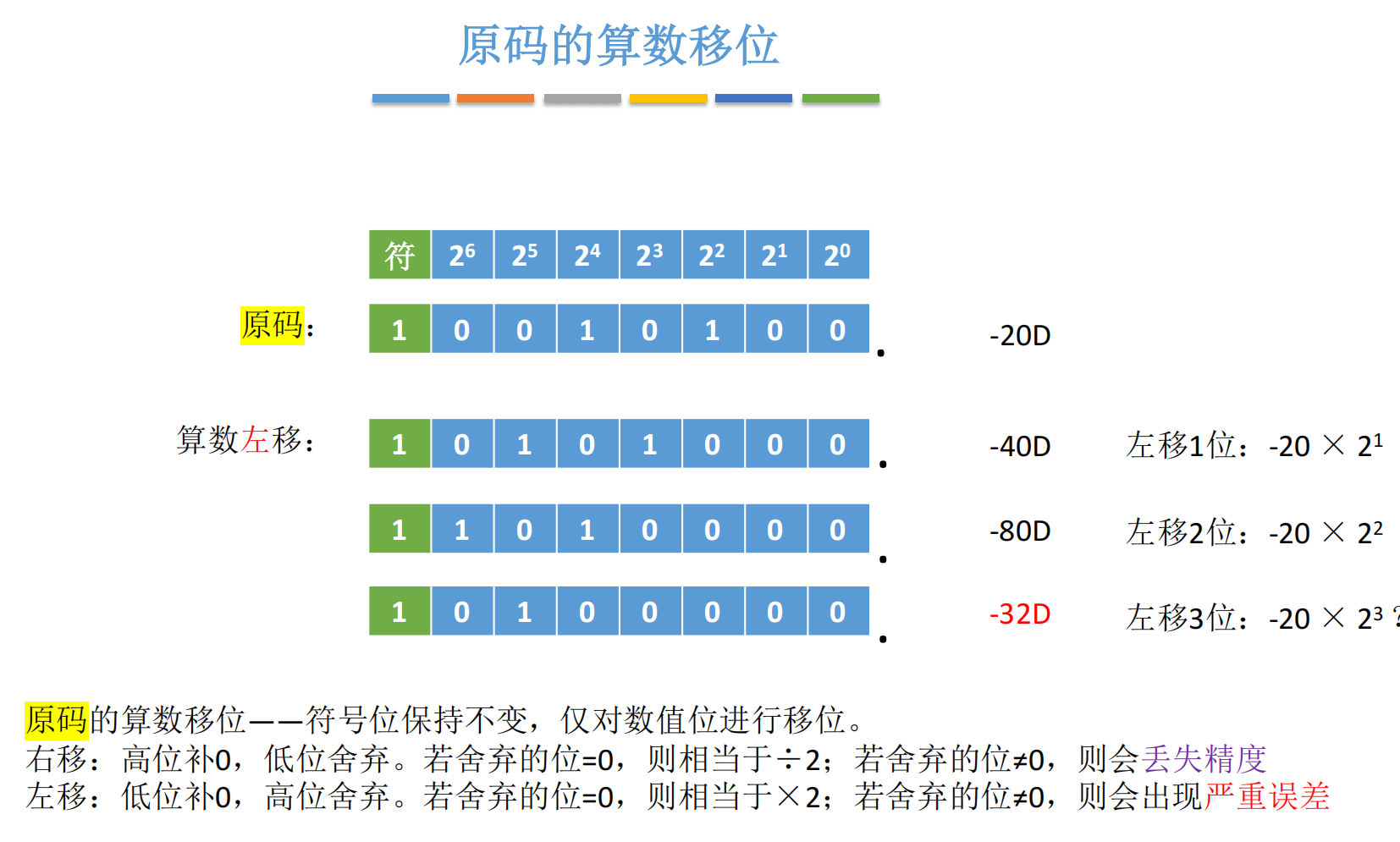
(2)算术左移(×2)
- 规则 :符号位不变,数值位左移 ,低位补 0 ,高位舍弃
- 效果 :
- 若舍弃位为 0 → 精确 ×2
- 若舍弃位为 1 → 溢出错误
示例 :−20-20−20 原码 10010100
- 左移 1 位 →
10101000= −40-40−40 ✅ - 左移 2 位 →
11010000= −80-80−80 ✅ - 再左移 1 位 →
10100000= −32-32−32 ❌(应为 −160-160−160,但 7 位数值位最大只能表示 127,160>127160 > 127160>127,最高位 1 被舍弃,结果严重错误)
💡 启示 :算术移位不能无限制使用,需警惕溢出与精度损失。
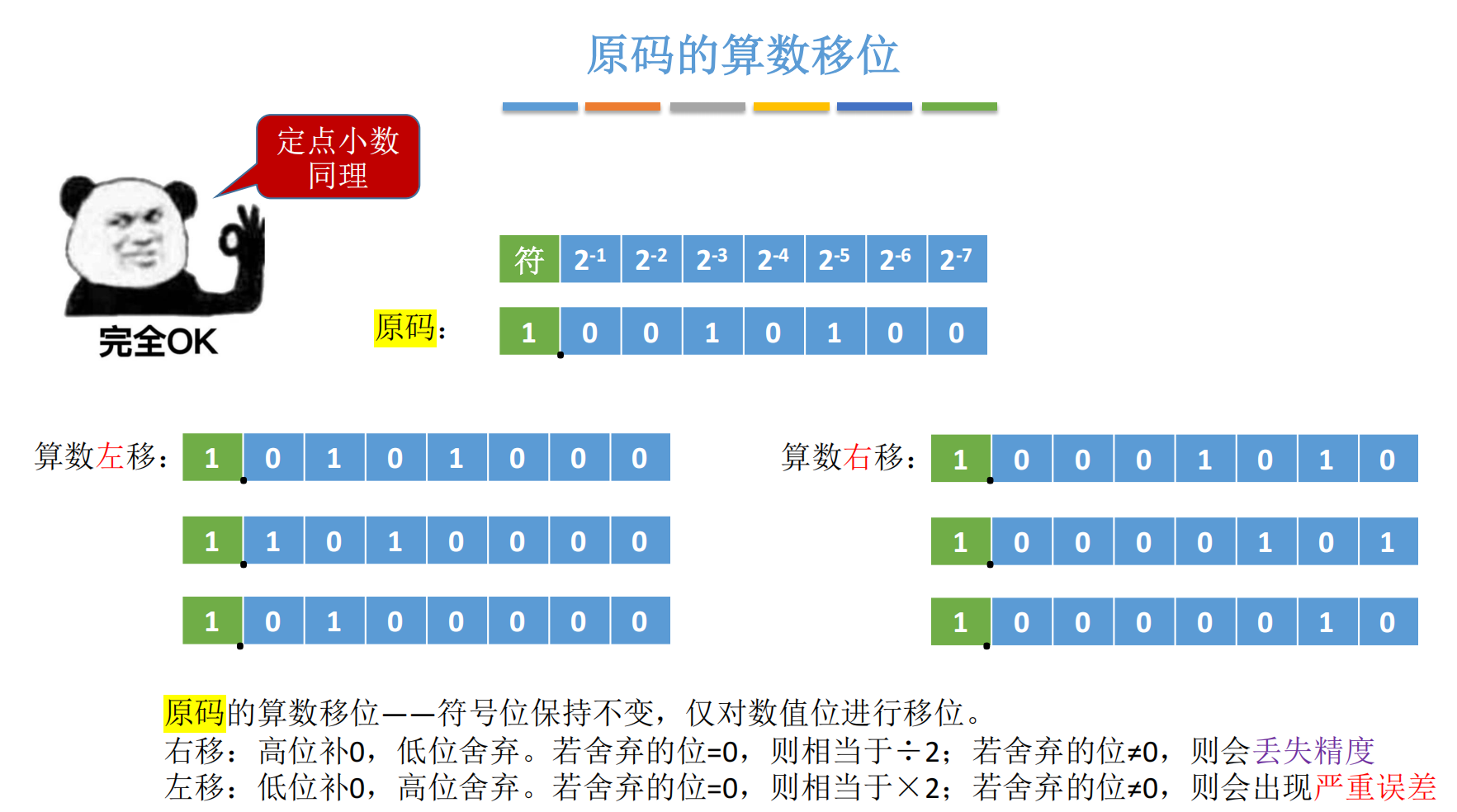
(3)定点小数同理
对于定点小数(如 Q7.8 格式),算术左移仍 ×2,右移仍 ÷2,规则一致。
2.2 反码的算术移位:负数全补 1
反码中,正数与原码相同;负数是符号位为 1,数值位按位取反。
- +20+20+20 反码:
00010100 - −20-20−20 反码:
11101011(原码10010100→ 数值位取反)
移位规则:
- 正数 :与原码相同,补 0
- 负数 :无论左移还是右移,空位均补 1
为什么?
因为反码的数值位是"取反"后的形式。若补 0,会破坏其与原码的对应关系,导致数值错误。
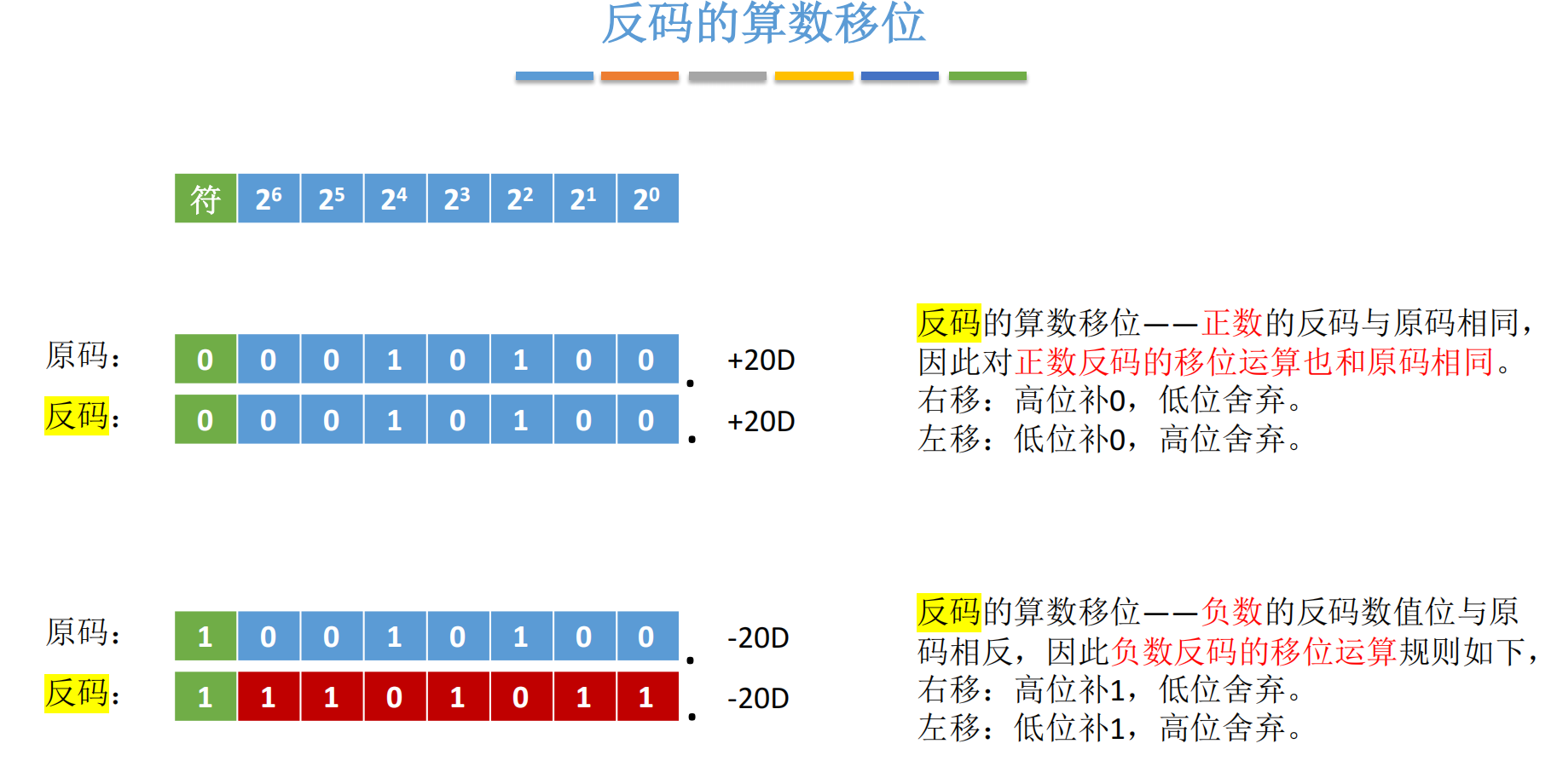
示例 :−20-20−20 反码 11101011
- 右移 1 位 →
11110101(高位补 1) - 左移 1 位 →
11010110(低位补 1)
✅ 补 1 能保证移位后数值仍符合反码定义。
2.3 补码的算术移位:左补 0,右补 1
补码是现代计算机的主流表示法。其负数由"反码 + 1"得到。
- +20+20+20 补码:
00010100 - −20-20−20 补码:
11101100(反码11101011+ 1)
关键观察:补码的结构特性
对负数补码,从最右边的 1 开始:
- 该 1 及其右侧:与原码相同
- 该 1 左侧:与反码相同
例如 −20-20−20 补码 11101100:
- 最右 1 在第 2 位(从 0 计)
- 右侧(第 0-1 位):
00= 原码00 - 左侧(第 3-7 位):
11101= 反码11101
移位规则:
- 正数:补 0(同原码)
- 负数 :
- 右移 :高位补 1(因左侧同反码)
- 左移 :低位补 0(因右侧同原码)
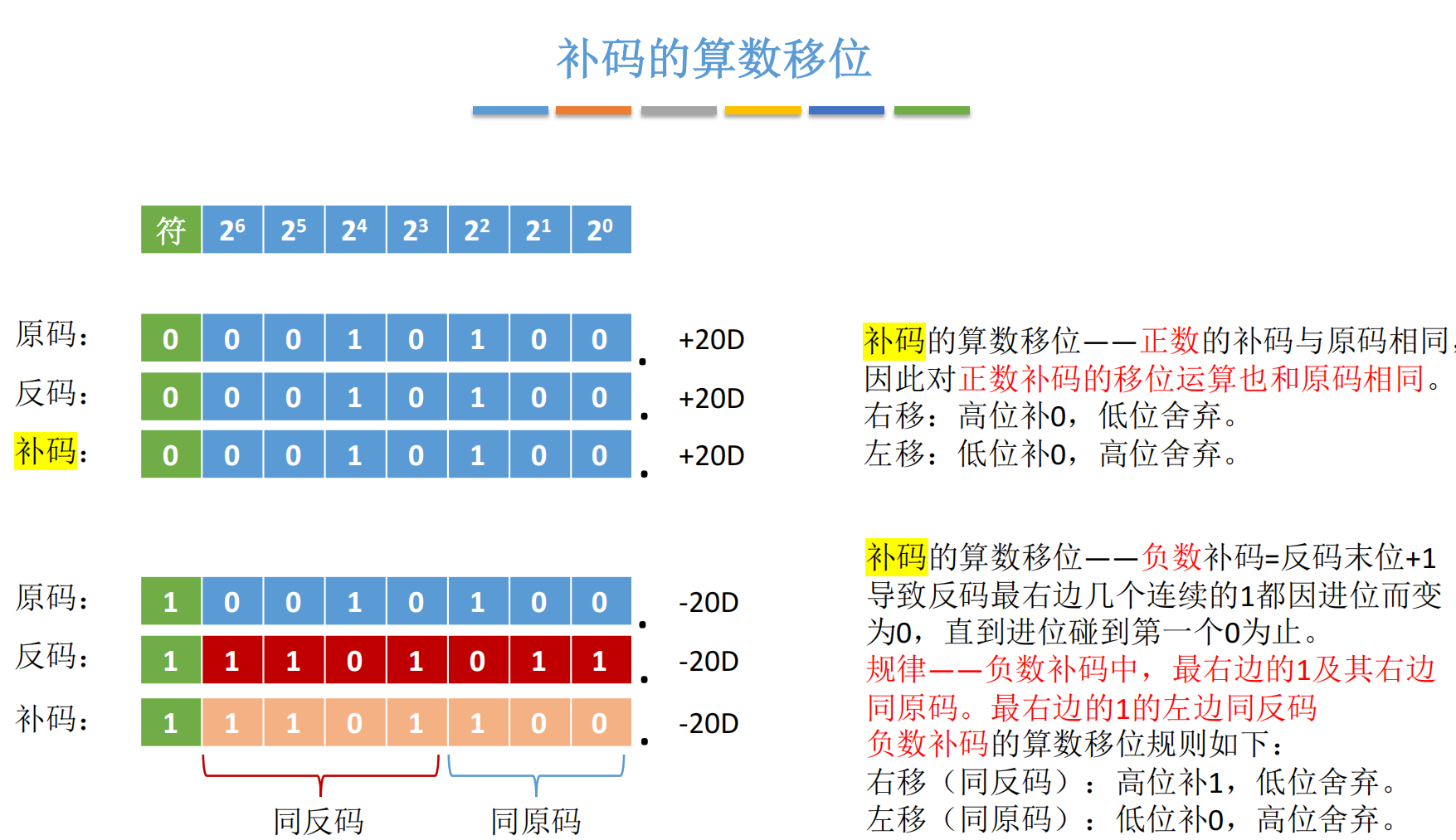
示例 :−20-20−20 补码 11101100
- 算术右移 1 位 →
11110110(高位补 1)= −10-10−10 ✅ - 算术左移 1 位 →
11011000(低位补 0)= −40-40−40 ✅
🔑 记忆口诀 :
补码负数,右移补 1,左移补 0。
2.4 算术移位总结表
| 编码 | 正数补位 | 负数补位 |
|---|---|---|
| 原码 | 补 0 | 补 0(仅数值位移,符号不动) |
| 反码 | 补 0 | 左/右均补 1 |
| 补码 | 补 0 | 左移补 0,右移补 1 |
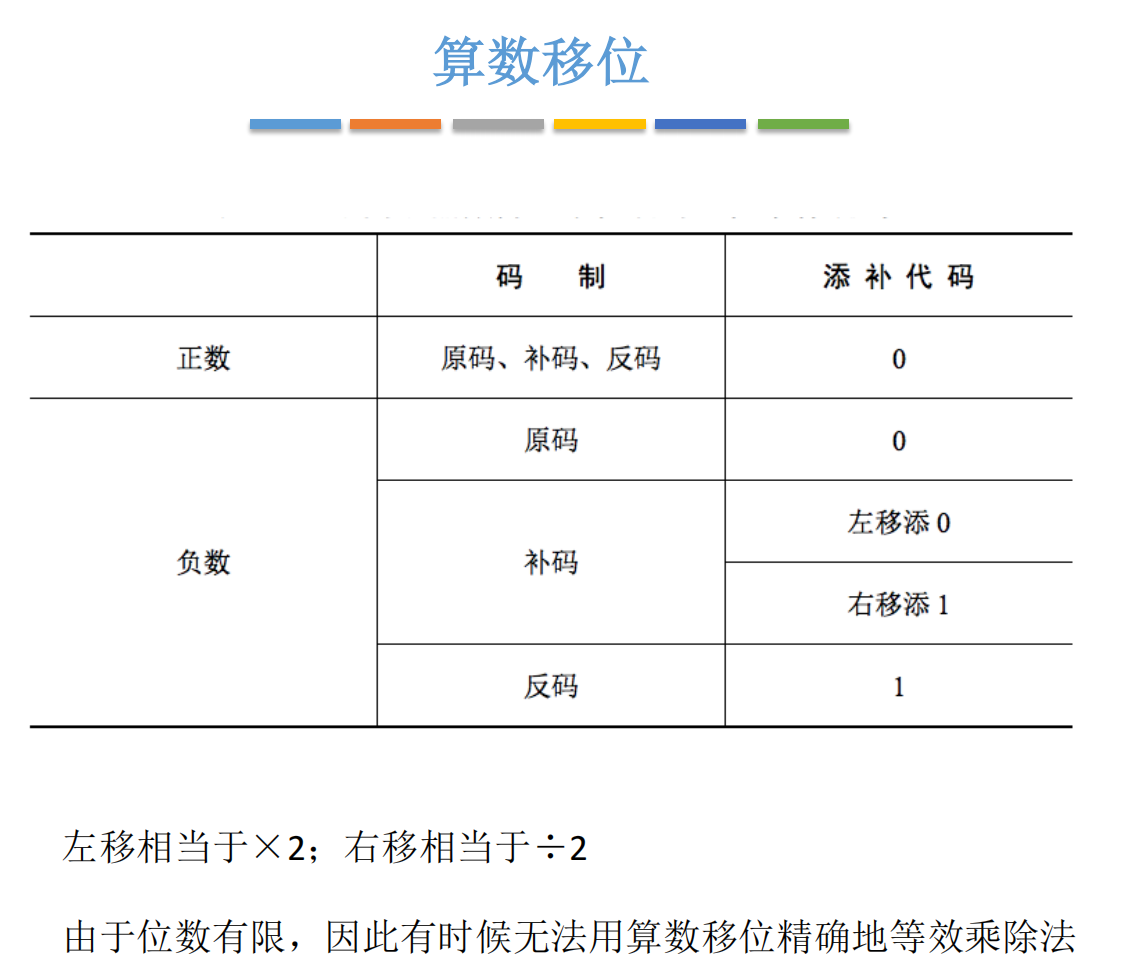 |
✅ 通用效果:算术左移 ≈ ×2,右移 ≈ ÷2(可能有误差)
2.5 应用:用移位实现乘法
计算机如何计算 −20×7-20 \times 7−20×7?
注意到:
7=20+21+22=1+2+4 7 = 2^0 + 2^1 + 2^2 = 1 + 2 + 4 7=20+21+22=1+2+4
所以:
−20×7=(−20×1)+(−20×2)+(−20×4) -20 \times 7 = (-20 \times 1) + (-20 \times 2) + (-20 \times 4) −20×7=(−20×1)+(−20×2)+(−20×4)
而:
- −20×1-20 \times 1−20×1 = 不移位
- −20×2-20 \times 2−20×2 = 左移 1 位
- −20×4-20 \times 4−20×4 = 左移 2 位
硬件只需:
- 对 −20-20−20 进行 0 位、1 位、2 位左移
- 将三个结果相加
💡 优势:移位电路比乘法器简单得多,这是早期 CPU 实现乘法的基础。
三、逻辑移位:无符号数的简单规则
逻辑移位不关心符号 ,适用于无符号数 或位操作。
3.1 规则极其简单:
- 左移:低位补 0,高位舍弃
- 右移:高位补 0,低位舍弃
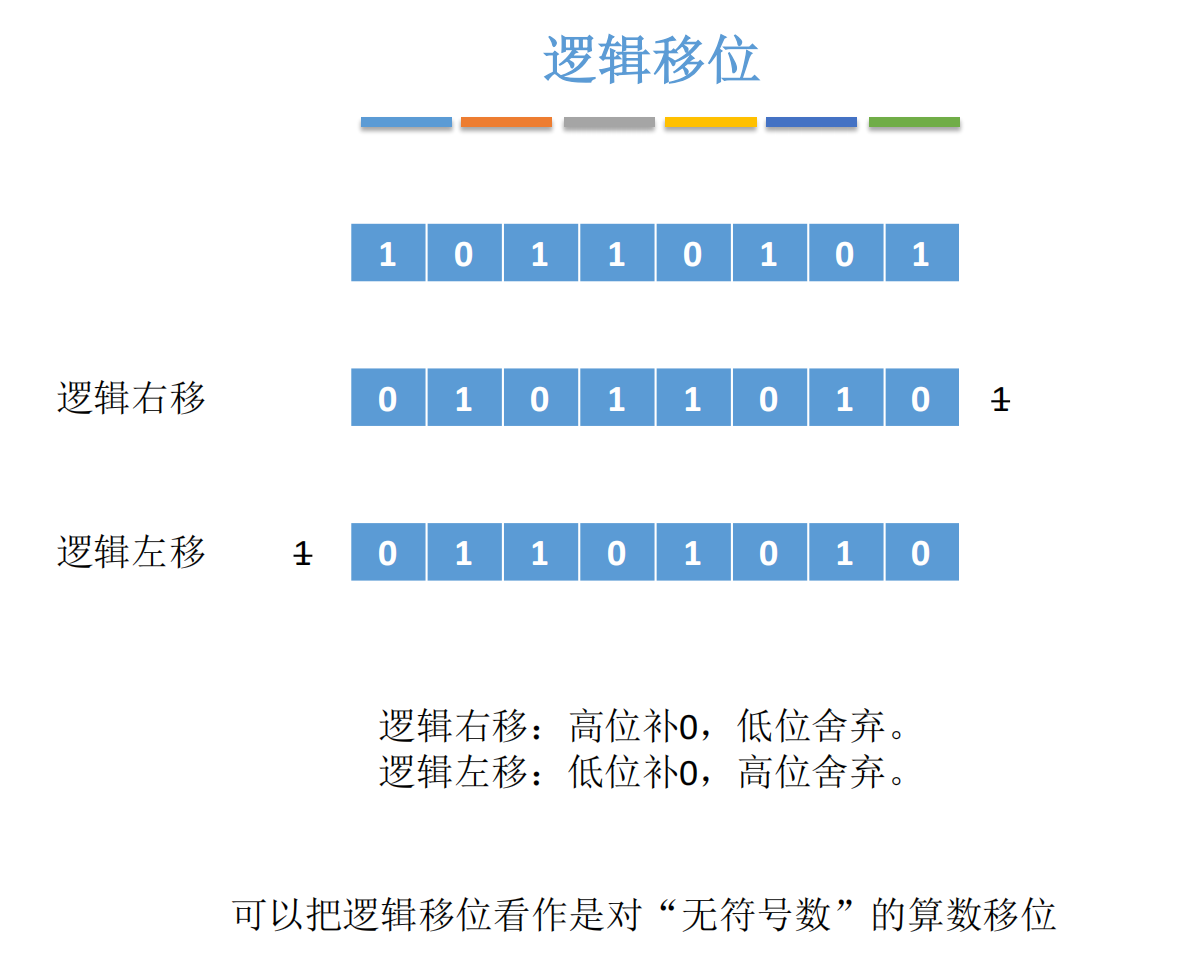
示例 :10110101(无符号数 181)
- 逻辑左移 1 位 →
01101010(106) - 逻辑右移 1 位 →
01011010(90)
📌 本质:逻辑移位 = 无符号数的算术移位。
3.2 应用:RGB 颜色值拼接
颜色常用 RGB 三通道表示,如 PaleTurquoise4 的 RGB = (102, 139, 139)。
要将其存入一个 24 位寄存器(高 8 位 R,中 8 位 G,低 8 位 B):
- R = 102 → 逻辑左移 16 位 →
01100110 00000000 00000000 - G = 139 → 逻辑左移 8 位 →
00000000 10001011 00000000 - B = 139 → 不移位 →
00000000 00000000 10001011
三者相加 → 01100110 10001011 10001011 = 0x668B8B
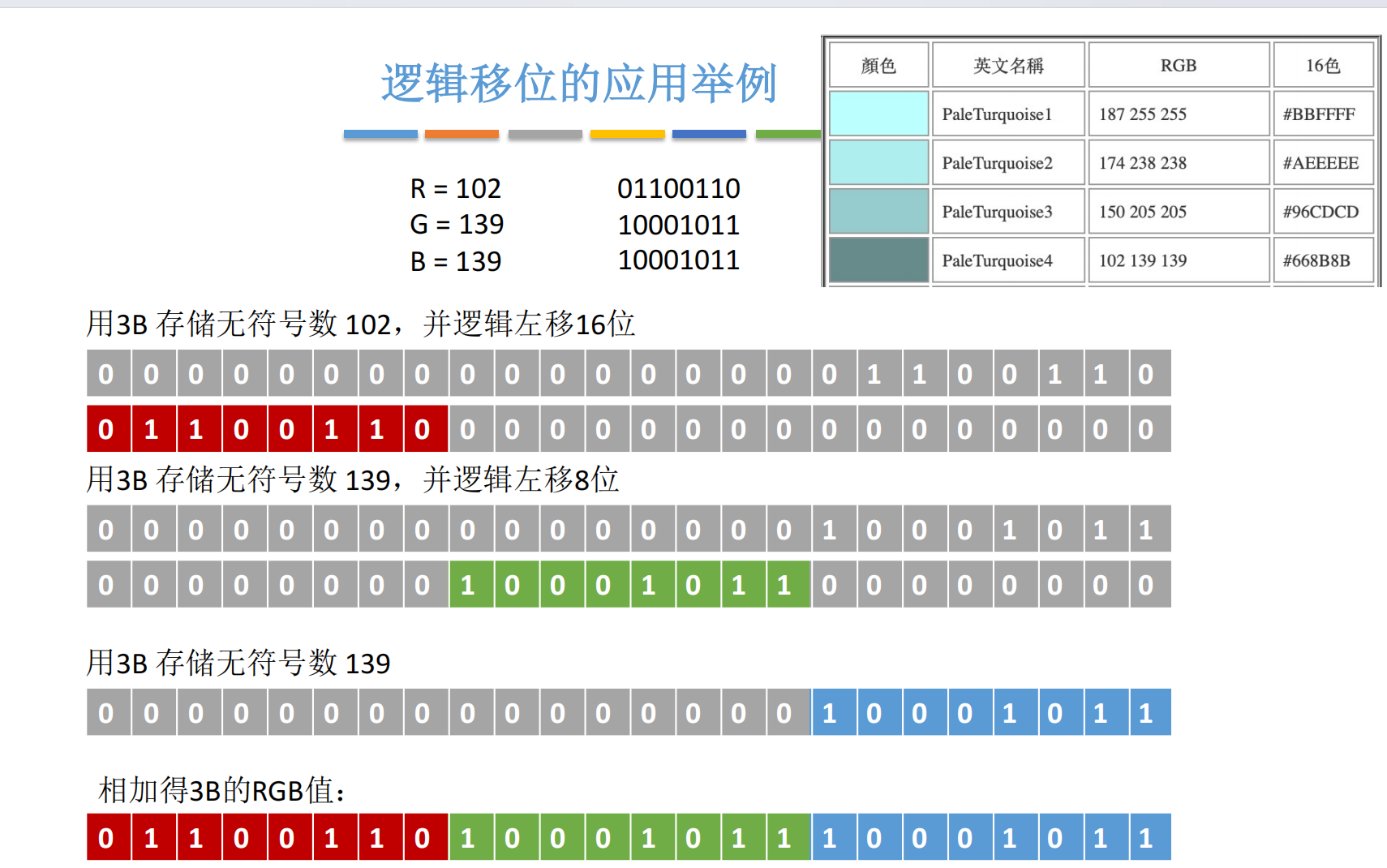
✅ 为什么用逻辑移位?
因为 R、G、B 是无符号整数,无需保留符号,高位补 0 正好形成拼接。
四、循环移位:移出的位"绕回来"
循环移位不丢弃任何位,而是将移出的位填补到空缺处 ,形成"循环"。
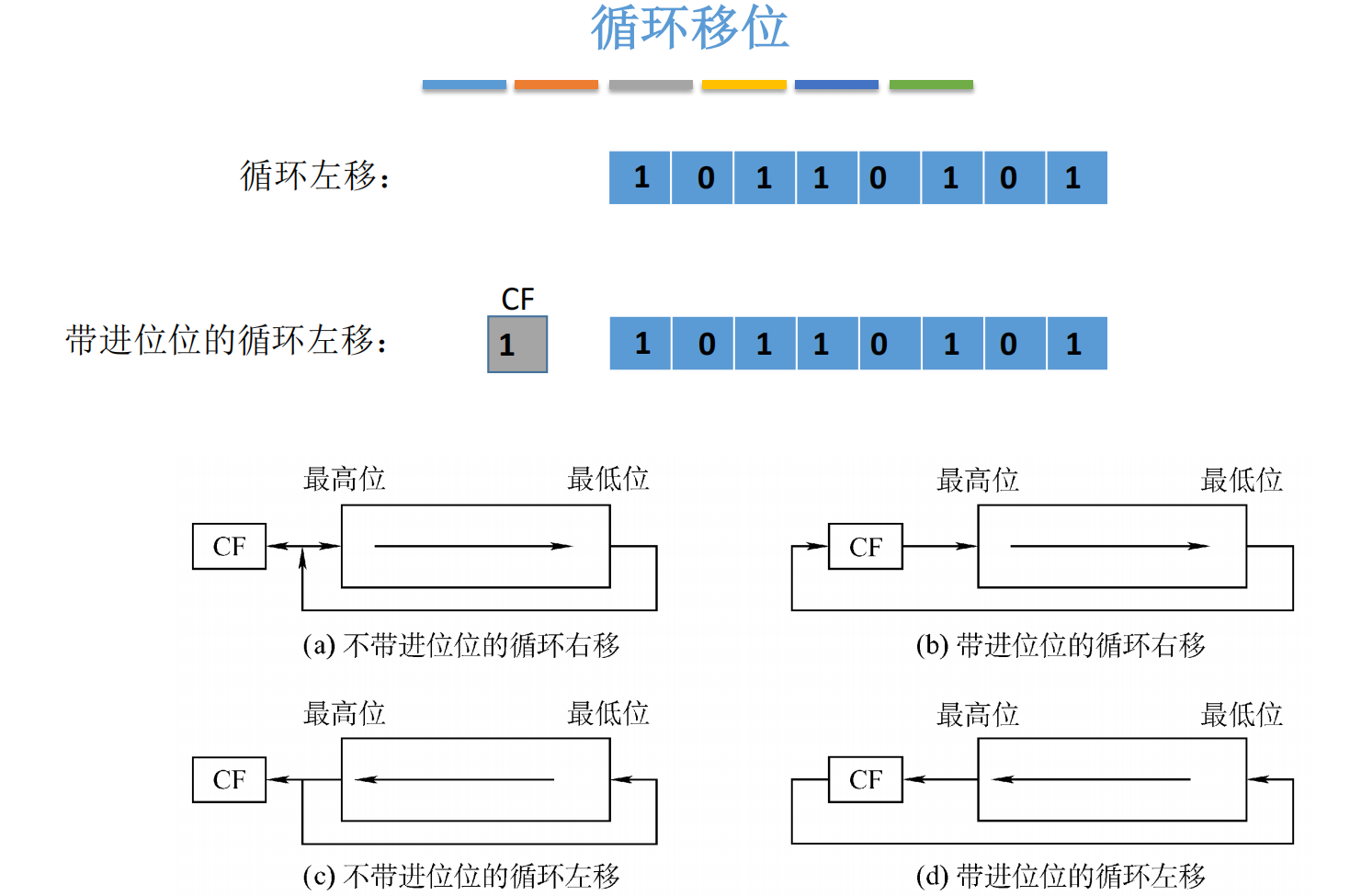
4.1 普通循环移位
- 循环左移:最高位 → 最低位
- 循环右移:最低位 → 最高位
示例 :10110101
- 循环左移 1 位 →
01101011 - 循环右移 1 位 →
11011010
🌟 用途:加密算法、哈希函数、位域旋转。
4.2 带进位位的循环移位
引入 进位标志位(CF),用于多字节运算。
- 带进位循环左移 :
- 数值最高位 → CF
- 原 CF → 数值最低位
- 带进位循环右移 :
- 数值最低位 → CF
- 原 CF → 数值最高位
示例 :CF=1,数值=10110101
- 带进位循环左移 → CF=1,数值=
01101011 - 带进位循环右移 → CF=1,数值=
11011010
💡 用途:实现超过寄存器宽度的大数移位。
五、总结与注意事项
-
算术移位是核心考点:
- 左移 ≈ ×2,右移 ≈ ÷2
- 补码负数:左移补 0,右移补 1
- 注意溢出与精度丢失
-
逻辑移位 规则统一:总是补 0,用于无符号数或位拼接
-
循环移位保留所有位,带进位版本用于大数运算
-
重要提醒 :
由于机器字长有限,移位不能完全等效乘除!
- 右移可能丢失小数部分
- 左移可能溢出高位