图像滤波:手撕五大经典滤波(均值 / 高斯 / 中值 / 双边 / 导向)【计算机视觉】
- [图像滤波(Image Filtering)](#图像滤波(Image Filtering))
-
- Ⅰ、引言
-
- [1. 图像滤波的作用](#1. 图像滤波的作用)
- [2. 五大经典滤波](#2. 五大经典滤波)
- Ⅱ、线性滤波
-
- [一、均值滤波(Mean Filter)](#一、均值滤波(Mean Filter))
-
- [1. 均值滤波核心概述](#1. 均值滤波核心概述)
- [2. 均值滤波的数学原理](#2. 均值滤波的数学原理)
- [3. 具体例题手动计算(直观理解核心逻辑)](#3. 具体例题手动计算(直观理解核心逻辑))
- [4. Python 代码实现均值滤波](#4. Python 代码实现均值滤波)
- [5. cv2.blur()函数](#5. cv2.blur()函数)
- 6.总结
- [二、高斯滤波(Gauss Filter)](#二、高斯滤波(Gauss Filter))
-
- [1. 高斯噪声](#1. 高斯噪声)
- [2. 高斯滤波器核心概述](#2. 高斯滤波器核心概述)
- [3. 高斯滤波的数学原理](#3. 高斯滤波的数学原理)
- [4. Python 代码实现高斯滤波](#4. Python 代码实现高斯滤波)
- 5.cv2.GaussianBlur()函数
- [6. 总结](#6. 总结)
- [均值滤波 vs 高斯滤波(处理高斯噪声)对比表](#均值滤波 vs 高斯滤波(处理高斯噪声)对比表)
- Ⅲ、非线性滤波
-
- [三、中值滤波(Median Filter)](#三、中值滤波(Median Filter))
-
- [1. 椒盐噪声](#1. 椒盐噪声)
- [2. 中值滤波器核心概述](#2. 中值滤波器核心概述)
- [3. 中值滤波的数学原理](#3. 中值滤波的数学原理)
-
- (1)核心数学表达式
- [(2)3×3 中值滤波分步实现](#(2)3×3 中值滤波分步实现)
- [(3)5×5 中值滤波补充说明](#(3)5×5 中值滤波补充说明)
- [4. Python 代码实现中值滤波](#4. Python 代码实现中值滤波)
- [5. cv2.medianBlur() 函数](#5. cv2.medianBlur() 函数)
- 6.总结
- [四、双边滤波(Bilateral Filter)](#四、双边滤波(Bilateral Filter))
-
- [1. 双边滤波器核心概述](#1. 双边滤波器核心概述)
- [2. 双边滤波的数学原理](#2. 双边滤波的数学原理)
-
- (1)核心数学表达式
- [(2)3×3 双边滤波分步实现](#(2)3×3 双边滤波分步实现)
- (3)大窗口双边滤波补充说明
- [3. 双边滤波主要应用场景](#3. 双边滤波主要应用场景)
- [4.Python 代码实现双边滤波](#4.Python 代码实现双边滤波)
-
- [(1)强高斯噪声滤波对比实验(双边滤波 vs 高斯滤波)](#(1)强高斯噪声滤波对比实验(双边滤波 vs 高斯滤波))
- [(2)强椒盐噪声滤波(双边滤波 vs 中值滤波)](#(2)强椒盐噪声滤波(双边滤波 vs 中值滤波))
- [5. cv2.bilateralFilter()函数](#5. cv2.bilateralFilter()函数)
- [6. 总结](#6. 总结)
- [五、导向滤波(Guided Filter)](#五、导向滤波(Guided Filter))
-
- [1. 导向滤波核心概述](#1. 导向滤波核心概述)
- [2. 导向滤波的数学原理](#2. 导向滤波的数学原理)
-
- (1)核心数学表达式
- [(2)3×3 导向滤波分步实现](#(2)3×3 导向滤波分步实现)
- (3)大窗口导向滤波补充说明
- [3. 高斯噪声环境下导向滤波与双边滤波的保边去噪性能对比实验](#3. 高斯噪声环境下导向滤波与双边滤波的保边去噪性能对比实验)
- [4. Python 代码实现导向滤波](#4. Python 代码实现导向滤波)
- [5. cv2.ximgproc.guidedFilter() 函数](#5. cv2.ximgproc.guidedFilter() 函数)
- [6. 总结](#6. 总结)
- 非线性滤波对比表格
- Ⅳ、图像滤波总结
图像滤波(Image Filtering)
图像滤波:用一个固定大小的滑动窗口(卷积核)遍历图像,根据窗口内邻域像素的统计或加权信息,重新计算并更新中心像素值的过程。
Ⅰ、引言
1. 图像滤波的作用
图像滤波的主要作用是提升图像质量 ,让后续任务更可靠。实际图像常包含噪声、纹理干扰或光照不均,这些都会影响检测、分割、识别等算法的性能。滤波能有效抑制噪声 、突出关键结构 ,是计算机视觉系统中不可或缺的预处理步骤。
2. 五大经典滤波
| 滤波类型 | 具体算法 | 核心原理 | 特点与适用场景 |
|---|---|---|---|
| 线性滤波 | 均值滤波 | 用邻域内所有像素的平均值替换中心像素 | 简单快速,计算高效;但会模糊图像边缘,细节丢失明显,适用于高斯噪声抑制、对图像模糊度要求不高的场景 |
| 线性滤波 | 高斯滤波 | 根据高斯分布给邻域像素分配不同权重,再进行加权平均 | 权重符合正态分布,图像模糊更自然柔和,边缘模糊程度低于均值滤波;是最常用的平滑滤波,广泛适用于各类高斯噪声抑制、图像预处理平滑场景 |
| 非线性滤波 | 中值滤波 | 取邻域像素的中位数作为中心像素新值 | 对椒盐噪声(黑白亮点/暗点)特别有效;能较好保留图像边缘细节,无线性模糊的拖影;适用于椒盐噪声去除、需要保留边缘的平滑场景 |
| 非线性滤波 | 双边滤波 | 同时考虑空间距离(邻域远近)和像素值相似度(色彩差异),进行加权平滑 | 兼具平滑降噪和边缘保留的特性(保边去噪);模糊程度低,细节保留好,适用于需要降噪且不希望边缘模糊的场景(如人像磨皮、景物细节保留) |
| 非线性滤波 | 导向滤波 | 利用引导图(通常为原图)计算局部线性模型,基于模型实现平滑加权 | 保边平滑效果更精确,优于双边滤波,且具有可解释性;常用于图像增强、抠图、去雾、边缘保留平滑等高精度图像处理任务 |
Ⅱ、线性滤波
一、均值滤波(Mean Filter)
1. 均值滤波核心概述
均值滤波(Mean Filter)是一种最基础的线性空间域滤波方法,核心思想是用图像中某像素点周围邻域内所有像素的灰度平均值,来替代该像素点的原始灰度值,从而实现对图像噪声的平滑(抑制)效果,尤其对高斯噪声有较好的处理表现。
2. 均值滤波的数学原理
(1)核心数学公式
均值滤波的数学表达分为离散域像素计算 和卷积核表达两种形式,本质等价。
(2)离散域像素直接计算
对于图像中的任意像素点 ( x , y ) (x, y) (x,y),其经过均值滤波后的输出灰度值 g ( x , y ) g(x, y) g(x,y) 计算公式为:
g ( x , y ) = 1 M × N ∑ i = − a a ∑ j = − b b f ( x + i , y + j ) g(x, y) = \frac{1}{M \times N} \sum_{i=-a}^{a} \sum_{j=-b}^{b} f(x+i, y+j) g(x,y)=M×N1i=−a∑aj=−b∑bf(x+i,y+j)
其中:
- f ( x , y ) f(x, y) f(x,y):图像的原始灰度值(输入图像)
- g ( x , y ) g(x, y) g(x,y):均值滤波后的灰度值(输出图像)
- M × N M \times N M×N:邻域窗口的尺寸(通常取奇数,如 3 × 3 3 \times 3 3×3、 5 × 5 5 \times 5 5×5, M = 2 a + 1 M=2a+1 M=2a+1, N = 2 b + 1 N=2b+1 N=2b+1)
- 1 M × N \frac{1}{M \times N} M×N1:归一化系数(保证滤波后图像灰度值范围不溢出)
(3)卷积核(模板)表达
均值滤波本质是一种卷积运算,对应的卷积核(均值模板)是一个所有元素值相等且满足归一化的矩阵。
以最常用的 3 × 3 3 \times 3 3×3 均值卷积核为例,其形式为:
K = 1 9 [ 1 1 1 1 1 1 1 1 1 ] K = \frac{1}{9} \begin{bmatrix} 1 & 1 & 1 \\ 1 & 1 & 1 \\ 1 & 1 & 1 \end{bmatrix} K=91 111111111
再如 5 × 5 5 \times 5 5×5 均值卷积核:
K = 1 25 [ 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 ] K = \frac{1}{25} \begin{bmatrix} 1 & 1 & 1 & 1 & 1 \\ 1 & 1 & 1 & 1 & 1 \\ 1 & 1 & 1 & 1 & 1 \\ 1 & 1 & 1 & 1 & 1 \\ 1 & 1 & 1 & 1 & 1 \end{bmatrix} K=251 1111111111111111111111111
卷积运算过程 :将卷积核中心与图像像素 ( x , y ) (x, y) (x,y) 对齐,卷积核各元素与对应位置的图像像素相乘,求和后得到的结果即为 g ( x , y ) g(x, y) g(x,y)(由于卷积核元素均为1,相乘求和等价于直接求和,再除以窗口像素总数)。
(4)边界处理说明
当卷积核滑动到图像边缘时,会出现邻域超出图像范围 的问题(比如图像左上角像素, 3 × 3 3 \times 3 3×3 邻域有一半在图像外),常用解决方法有:
- 边界填充(最常用):在图像边缘填充0(零填充)、重复边缘像素(复制填充)、镜像填充等,使卷积核能够完整滑动;
- 忽略边缘像素:直接舍弃图像边缘无法完整计算的像素,输出图像尺寸略小于输入图像;
- 裁剪卷积核:边缘位置使用缩小的邻域窗口计算(不推荐,会导致边缘效果不一致)。
3. 具体例题手动计算(直观理解核心逻辑)
为了更清晰地掌握均值滤波的计算过程,我们以 3 × 3 3 \times 3 3×3 邻域窗口为例,进行手动分步计算,无边界问题(选取图像内部像素,无需填充)。
(1)例题条件
给定一张 5 × 5 5 \times 5 5×5 的灰度图像(像素值为0-255之间的整数),如下所示(矩阵形式,行号0-4,列号0-4):
f ( x , y ) = [ 10 20 30 40 50 15 25 35 45 55 20 30 40 50 60 25 35 45 55 65 30 40 50 60 70 ] f(x, y) = \begin{bmatrix} 10 & 20 & 30 & 40 & 50 \\ 15 & 25 & 35 & 45 & 55 \\ 20 & 30 & \textbf{40} & 50 & 60 \\ 25 & 35 & 45 & 55 & 65 \\ 30 & 40 & 50 & 60 & 70 \end{bmatrix} f(x,y)= 10152025302025303540303540455040455055605055606570
要求:使用 3 × 3 3 \times 3 3×3 均值滤波,计算中心像素 ( 2 , 2 ) (2, 2) (2,2)(像素值为40,加粗标注)的滤波后输出值 g ( 2 , 2 ) g(2, 2) g(2,2)。
(2)分步计算过程
步骤1:确定邻域窗口范围
根据 3 × 3 3 \times 3 3×3 窗口要求,中心像素 ( 2 , 2 ) (2, 2) (2,2) 对应的邻域窗口为行号1-3、列号1-3的像素区域,提取该邻域窗口的像素值:
邻域窗口 = [ 25 35 45 30 40 50 35 45 55 ] \text{邻域窗口} = \begin{bmatrix} 25 & 35 & 45 \\ 30 & 40 & 50 \\ 35 & 45 & 55 \end{bmatrix} 邻域窗口= 253035354045455055
步骤2:计算邻域窗口内所有像素的总和
将窗口内9个像素值依次相加:
S = 25 + 35 + 45 + 30 + 40 + 50 + 35 + 45 + 55 = 360 S = 25 + 35 + 45 + 30 + 40 + 50 + 35 + 45 + 55=360 S=25+35+45+30+40+50+35+45+55=360
步骤3:除以窗口像素总数(归一化),得到滤波结果
3 × 3 3 \times 3 3×3 窗口的像素总数为9,因此均值为:
g ( 2 , 2 ) = S 9 = 360 9 = 40 g(2, 2) = \frac{S}{9} = \frac{360}{9} = 40 g(2,2)=9S=9360=40
(3)例题扩展说明
- 本例题中中心像素滤波后值仍为40,是因为邻域像素呈均匀递增分布,平均值恰好等于原始像素值,实际含噪图像中这种情况极少;
- 若中心像素原始值为60(模拟噪声干扰),邻域总和仍为360,则滤波后值为40,可见均值滤波会将噪声像素拉回到邻域平均水平,实现噪声抑制;
- 若使用 5 × 5 5 \times 5 5×5 窗口计算该像素,邻域总和为1000,均值为 1000 / 25 = 40 1000/25=40 1000/25=40,同样可得到稳定结果,但窗口越大,越容易抹平周边像素的差异。
(4)例题代码验证
python
import numpy as np
# 1. 构建例题中的5x5原始图像矩阵
original_image = np.array([
[10, 20, 30, 40, 50],
[15, 25, 35, 45, 55],
[20, 30, 40, 50, 60],
[25, 35, 45, 55, 65],
[30, 40, 50, 60, 70]
], dtype=np.uint8)
# 2. 提取3x3邻域窗口(对应中心像素(2,2),行1-3,列1-3)
neighborhood = original_image[1:4, 1:4] # 切片:左闭右开,1:4对应索引1、2、3
# 3. 计算邻域窗口的总和与平均值(模拟均值滤波核心计算)
neighborhood_sum = np.sum(neighborhood)
neighborhood_mean = np.mean(neighborhood)
# 4. 打印结果,验证手动计算
print("=== 均值滤波例题验证结果 ===")
print(f"3x3邻域窗口像素矩阵:\n{neighborhood}")
print(f"邻域窗口像素总和:{neighborhood_sum}")
print(f"邻域窗口像素平均值(滤波后结果):{neighborhood_mean}")
4. Python 代码实现均值滤波
python
import numpy as np
import cv2
import matplotlib.pyplot as plt
# -------- 核心:添加Matplotlib中文显示配置 --------
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
def manual_mean_filter(image, kernel_size=3):
if kernel_size % 2 == 0:
raise ValueError("卷积核尺寸必须为奇数,请修改kernel_size参数")
h, w = image.shape
pad_size = kernel_size // 2
padded_image = np.pad(image, pad_width=pad_size, mode='edge')
output_image = np.zeros_like(image)
for y in range(h):
for x in range(w):
neighborhood = padded_image[y:y+kernel_size, x:x+kernel_size]
output_image[y, x] = np.mean(neighborhood)
return output_image.astype(np.uint8)对def manual_mean_filter(image, kernel_size=3):的解析
python
if kernel_size % 2 == 0:
raise ValueError("卷积核尺寸必须为奇数,请修改kernel_size参数")- 逻辑:使用取模运算
%判断kernel_size是否为偶数(对2取模结果为0即为偶数)。 - 作用:
- 均值滤波窗口需要有唯一的中心像素(如3×3窗口中心是第2行第2列),偶数尺寸窗口无明确中心,会导致滤波逻辑混乱。
- 传入偶数时抛出明确异常,避免后续代码运行出现未知问题。
python
h, w = image.shape
pad_size = kernel_size // 2h, w = image.shape:从输入灰度图像的shape属性中解包出图像高度(h)和宽度(w)。pad_size = kernel_size // 2:- 核心作用:保证滤波后输出图像尺寸与输入图像完全一致,避免尺寸缩小。
- 示例:kernel_size=3时pad_size=1,kernel_size=5时pad_size=2。
python
padded_image = np.pad(image, pad_width=pad_size, mode='edge')- 功能:调用
numpy.pad()对原始图像进行边界填充。 - 参数说明:
pad_width=pad_size:上下左右四个方向各填充pad_size个像素。mode='edge':填充模式为「边缘复制」,使用图像边缘像素值填充边界,减少边缘滤波失真。
- 核心作用:
- 解决卷积核滑动到图像边缘时无法提取完整邻域窗口的问题。
- 保证输出图像尺寸与输入图像一致,避免尺寸损失。
python
output_image = np.zeros_like(image)- 创建与输入图像
image形状相同、数据类型相同的全零数组,用于存储滤波结果。
python
for y in range(h):
for x in range(w):
neighborhood = padded_image[y:y+kernel_size, x:x+kernel_size]
output_image[y, x] = np.mean(neighborhood)- 核心逻辑:「滑动窗口遍历」+「邻域像素求平均」,对应均值滤波的数学原理。
- 逐行解析:
- 双重循环遍历:外层循环遍历图像每一行,内层循环遍历图像每一列,实现卷积核逐行逐列滑动。
- 提取邻域窗口:通过numpy切片从填充后图像中提取
kernel_size×kernel_size的邻域像素。 - 邻域求平均:调用
np.mean()计算邻域内像素平均值,赋值给输出图像对应位置,实现噪声「拉平」降噪。
python
return output_image.astype(np.uint8)- 将输出图像转换为
uint8类型(8位无符号整数),符合图像存储和显示的标准格式。
python
img_gray = cv2.imread("img/lena.jpeg", cv2.IMREAD_GRAYSCALE)
if img_gray is None:
raise FileNotFoundError("未找到测试图像,请确保img/test_image.jpg在对应目录下")
# 添加高斯噪声
np.random.seed(42)
noise = np.random.normal(0, 20, img_gray.shape).astype(np.uint8)
noisy_img = cv2.add(img_gray, noise)
# 执行均值滤波
filtered_img_3 = manual_mean_filter(noisy_img, kernel_size=3)
filtered_img_5 = manual_mean_filter(noisy_img, kernel_size=5)
# 可视化(中文标题可正常显示,无乱码)
plt.figure(figsize=(16, 8))
plt.subplot(2, 2, 1)
plt.imshow(img_gray, cmap='gray')
plt.title("原始灰度图像", fontsize=12) # 中文标题
plt.axis('off')
plt.subplot(2, 2, 2)
plt.imshow(noisy_img, cmap='gray')
plt.title("添加高斯噪声后的图像", fontsize=12) # 中文标题
plt.axis('off')
plt.subplot(2, 2, 3)
plt.imshow(filtered_img_3, cmap='gray')
plt.title("手动实现3x3均值滤波结果", fontsize=12) # 中文标题
plt.axis('off')
plt.subplot(2, 2, 4)
plt.imshow(filtered_img_5, cmap='gray')
plt.title("手动实现5x5均值滤波结果", fontsize=12) # 中文标题
plt.axis('off')
plt.tight_layout()
plt.show()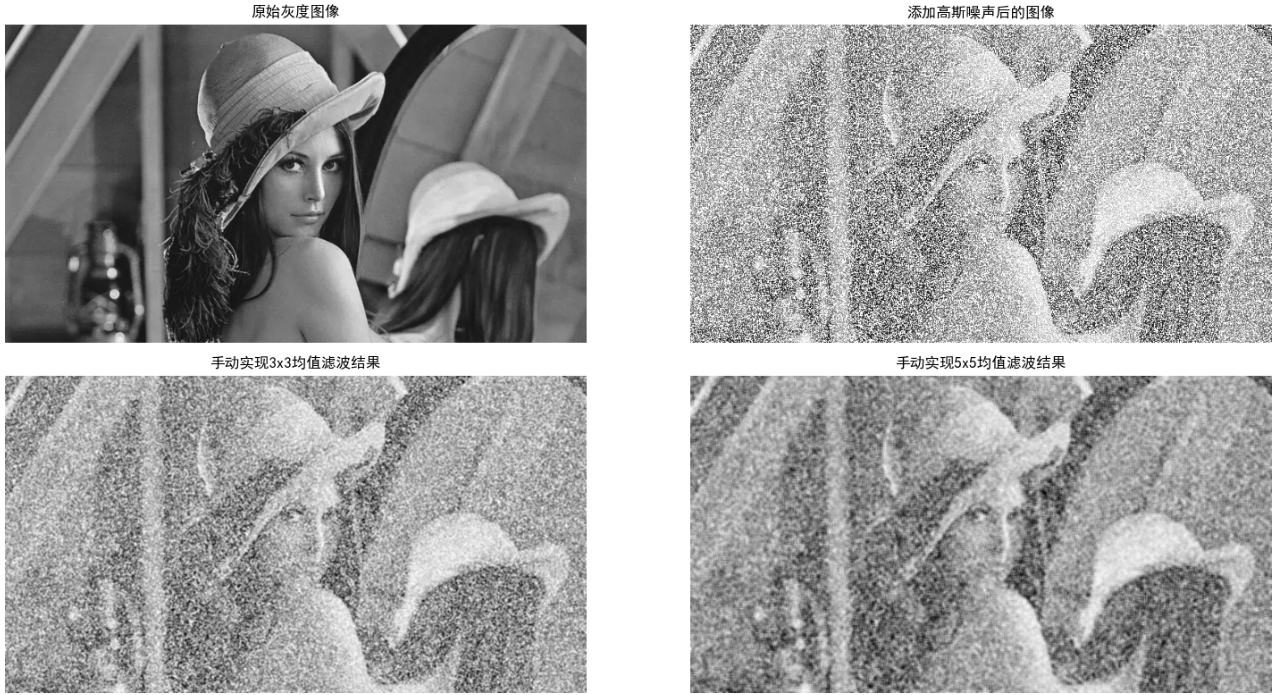
5. cv2.blur()函数
cv2.blur() 是 OpenCV 库中专门用于实现「均值滤波」的内置函数,核心作用是对图像进行降噪和平滑处理,底层采用 C++ 优化实现,运行高效,是图像处理中抑制高斯噪声、弱化图像细节边缘的常用工具。
python
dst = cv2.blur(src, ksize, anchor=None, borderType=None)核心必选参数(实际开发中最常用)
| 参数 | 含义与说明 |
|---|---|
src |
输入图像(待滤波的图像),支持 uint8、float32 等数据类型,OpenCV 读取的灰度图 / 彩色图均可直接传入。 |
ksize |
滤波窗口(又称卷积核)尺寸,格式为 (width, height)(宽度 × 高度),要求为正整数。 常用正方形奇数窗口:(3, 3)、(5, 5)、(7, 7),窗口越大,降噪 / 平滑效果越强,图像细节丢失越多。 |
可选参数(默认值满足常规需求)
| 参数 | 含义与说明 |
|---|---|
anchor |
窗口锚点(滤波时的参考中心),默认值 (-1, -1),表示锚点位于窗口中心,无需手动修改。 |
borderType |
边界填充方式,默认值 cv2.BORDER_DEFAULT(等价于边缘复制填充),解决图像边缘无法提取完整窗口的问题,避免边缘像素滤波失效。 |
返回值 dst
滤波后的输出图像,格式、尺寸与输入图像 src 完全一致:
- 输入灰度图,返回灰度图;输入 BGR 彩色图,返回 BGR 彩色图。
- 像素值已完成邻域平均更新,保留 OpenCV 默认图像格式,可直接用于后续其他 OpenCV 图像处理函数。
这时我们就可以对上面的代码进行优化
python
# 转换为灰度图(可选,也可直接处理彩色图)
img_gray = cv2.imread("img/lena.jpeg", cv2.IMREAD_GRAYSCALE)
# BGR 转 RGB(适配Matplotlib显示彩色图像)
img_rgb = cv2.cvtColor(img, cv2.COLOR_BGR2RGB)
# 添加高斯噪声
np.random.seed(42)
noise = np.random.normal(0, 20, img.shape).astype(np.uint8)
noisy_img = cv2.add(img, noise)
noisy_img_rgb = cv2.cvtColor(noisy_img, cv2.COLOR_BGR2RGB)
# 执行OpenCV均值滤波
filtered_img_3 = cv2.blur(noisy_img, ksize=(3, 3))
filtered_img_3_rgb = cv2.cvtColor(filtered_img_3, cv2.COLOR_BGR2RGB)
filtered_img_5 = cv2.blur(noisy_img, ksize=(5, 5))
filtered_img_5_rgb = cv2.cvtColor(filtered_img_5, cv2.COLOR_BGR2RGB)- 先通过
cv2.imread()完成图像读取(含可选灰度图、核心彩色图),再通过cv2.cvtColor()将OpenCV默认的BGR格式转换为Matplotlib兼容的RGB格式(适配可视化); - 接着通过
np.random.normal()生成高斯噪声、cv2.add()将噪声叠加到彩色原图制造带噪图像; - 最后通过核心滤波函数
cv2.blur()分别以3×3和5×5窗口执行均值滤波实现降噪,并再次通过cv2.cvtColor()将带噪图、滤波图统一转换为RGB格式 - 「图像读取→格式适配→噪声添加→均值滤波→显示适配」,为后续可视化对比降噪效果做好准备。
python
plt.figure(figsize=(16, 8))
plt.subplot(2, 2, 1)
plt.imshow(img_rgb)
plt.title("原始彩色图像(Lena)", fontsize=12)
plt.axis('off')
plt.subplot(2, 2, 2)
plt.imshow(noisy_img_rgb)
plt.title("添加高斯噪声后的Lena图像", fontsize=12)
plt.axis('off')
plt.subplot(2, 2, 3)
plt.imshow(filtered_img_3_rgb)
plt.title("OpenCV 3x3均值滤波结果", fontsize=12)
plt.axis('off')
plt.subplot(2, 2, 4)
plt.imshow(filtered_img_5_rgb)
plt.title("OpenCV 5x5均值滤波结果", fontsize=12)
plt.axis('off')
plt.tight_layout()
plt.show()
6.总结
- 均值滤波主要解决图像中的高斯噪声 (又称正态噪声)干扰问题,同时可辅助解决图像中微小纹理、杂点带来的视觉杂乱问题
- 均值滤波的核心逻辑是 「滑动窗口 + 邻域等权平均」,通过cv2.blur()函数自动实现,无需手动干预
- 均值滤波的数学本质是 「邻域像素的算术平均值计算」,通过对局部窗口内的像素值进行等权求和再平均,用统计平均结果抵消单个噪声像素的极端值,从而抹平像素值的剧烈波动,实现降噪和平滑,其数学表达简洁且易于理解。
二、高斯滤波(Gauss Filter)
1. 高斯噪声
python
# 单元格1:导入依赖库 + 创建img文件夹(若不存在,避免路径报错)+ 新增高斯噪声函数
import numpy as np
import cv2
import matplotlib.pyplot as plt
# 配置Matplotlib中文显示(可选,避免图表中文乱码)
plt.rcParams["font.sans-serif"] = ["SimHei"]
plt.rcParams["axes.unicode_minus"] = False
python
def add_gaussian_noise(image, mean=0, var=0.005):
image_float = np.array(image, dtype=np.float32) / 255.0
noise = np.random.normal(mean, np.sqrt(var), image_float.shape)
noisy_image_float = np.clip(image_float + noise, 0, 1)
noisy_image = np.uint8(noisy_image_float * 255.0)
noise_normalized = np.zeros_like(noise)
if len(noise.shape) == 3: # 彩色图(H,W,3)
for channel in range(3):
channel_noise = noise[..., channel]
chan_min, chan_max = np.min(channel_noise), np.max(channel_noise)
if chan_max - chan_min != 0:
noise_normalized[..., channel] = (channel_noise - chan_min) / (chan_max - chan_min)
else:
noise_normalized[..., channel] = channel_noise
else: # 灰度图(H,W)
noise_min, noise_max = np.min(noise), np.max(noise)
if noise_max - noise_min != 0:
noise_normalized = (noise - noise_min) / (noise_max - noise_min)
else:
noise_normalized = noise
noise_uint8 = np.uint8(noise_normalized * 255.0)
return noisy_image, noise_uint8-
add_gaussian_noise函数解析该函数用于给灰度/彩色图像添加高斯噪声,返回带噪声的图像和可单独可视化的归一化噪声矩阵。
-
- 图像预处理:转换为浮点型并归一化
将输入图像转换为float32类型,并除以 255 归一化到 [0, 1] 区间,避免噪声计算时出现溢出或失真问题。
- 图像预处理:转换为浮点型并归一化
python
image_float = np.array(image, dtype=np.float32) / 255.0-
- 生成高斯噪声矩阵
利用np.random.normal生成符合高斯分布的噪声,噪声的尺寸与预处理后的图像完全一致(彩色图自动适配 3 通道,灰度图适配 2 维尺寸),其中:
- 生成高斯噪声矩阵
mean:高斯噪声的均值,默认 0,避免图像整体明暗偏移np.sqrt(var):高斯噪声的标准差,由方差开方得到,控制噪声强度
python
noise = np.random.normal(mean, np.sqrt(var), image_float.shape)-
- 图像添加噪声并裁剪合法范围
将预处理后的图像与高斯噪声相加,再通过np.clip裁剪到 [0, 1] 区间,确保数值不会超出浮点型图像的合法范围,避免出现异常明暗区域。
- 图像添加噪声并裁剪合法范围
python
noisy_image_float = np.clip(image_float + noise, 0, 1)-
- 转换回 uint8 格式图像(用于后续处理)
将浮点型带噪声图像乘以 255 还原到 [0, 255] 区间,再转换为uint8类型(OpenCV 图像默认格式),得到可直接用于后续滤波等处理的带噪声图像。
- 转换回 uint8 格式图像(用于后续处理)
python
noisy_image = np.uint8(noisy_image_float * 255.0) -
- 初始化噪声归一化矩阵
创建一个与原始噪声矩阵尺寸、类型完全一致的全 0 矩阵,用于存储后续归一化后的噪声数据,为单独可视化噪声做准备。
- 初始化噪声归一化矩阵
python
noise_normalized = np.zeros_like(noise)-
- 彩色图噪声归一化(多通道独立处理)
针对 3 通道彩色图像(形状为 H,W,3),遍历每个颜色通道进行独立归一化:
- 彩色图噪声归一化(多通道独立处理)
- 提取当前通道的噪声数据
- 计算该通道噪声的最大值和最小值
- 若最大值与最小值不相等,通过 Min-Max 归一化将通道噪声转换到 [0, 1] 区间
- 若最大值与最小值相等(无有效噪声),直接保留原始噪声数据
python
if len(noise.shape) == 3: # 彩色图(H,W,3)
for channel in range(3):
channel_noise = noise[..., channel]
chan_min, chan_max = np.min(channel_noise), np.max(channel_noise)
if chan_max - chan_min != 0:
noise_normalized[..., channel] = (channel_noise - chan_min) / (chan_max - chan_min)
else:
noise_normalized[..., channel] = channel_noise-
- 灰度图噪声归一化(单通道处理)
针对 2 维灰度图像(形状为 H,W),直接对整个噪声矩阵进行 Min-Max 归一化:
- 灰度图噪声归一化(单通道处理)
- 计算灰度噪声的最大值和最小值
- 若最大值与最小值不相等,转换到 [0, 1] 区间
- 若最大值与最小值相等,直接保留原始噪声数据
python
else: # 灰度图(H,W)
noise_min, noise_max = np.min(noise), np.max(noise)
if noise_max - noise_min != 0:
noise_normalized = (noise - noise_min) / (noise_max - noise_min)
else:
noise_normalized = noise-
- 转换噪声矩阵为可可视化格式
将归一化到 [0, 1] 区间的噪声矩阵乘以 255,再转换为uint8类型,得到可直接用plt.imshow可视化的噪声图像。
- 转换噪声矩阵为可可视化格式
python
noise_uint8 = np.uint8(noise_normalized * 255.0)-
- 函数返回结果
返回两个核心结果,满足不同使用需求:
- 函数返回结果
noisy_image:带高斯噪声的原始格式图像(uint8 类型),可用于后续滤波、检测等图像处理流程noise_uint8:归一化后的单独噪声图像(uint8 类型),可用于直观展示高斯噪声的分布样貌
python
return noisy_image, noise_uint82. 高斯滤波器核心概述
高斯滤波是一种基于高斯函数(正态分布)的线性平滑滤波,常用于消除高斯噪声(如相机传感器噪声)。
它的核心特点是:对图像中距离中心点越近的像素,赋予越高的权重,既平滑图像又能更好地保留边缘细节(比均值滤波更柔和)。

3. 高斯滤波的数学原理
(1)核心数学公式
高斯滤波的权重核(卷积核)由二维高斯函数 生成:
G ( x , y ) = 1 2 π σ 2 e − x 2 + y 2 2 σ 2 G(x,y) = \frac{1}{2\pi\sigma^2} e^{-\frac{x^2 + y^2}{2\sigma^2}} G(x,y)=2πσ21e−2σ2x2+y2
- x , y x,y x,y:核内像素相对于中心点的坐标(如3×3核的中心点坐标为(0,0),周围为(±1,±1));
- σ \sigma σ:高斯分布的标准差, σ \sigma σ越大,核的"模糊程度"越强。
当 σ = 1 \sigma=1 σ=1 时,公式简化为:
G ( x , y ) = 1 2 π e − x 2 + y 2 2 G(x,y) = \frac{1}{2\pi} e^{-\frac{x^2 + y^2}{2}} G(x,y)=2π1e−2x2+y2
其中: ( x , y ) (x,y) (x,y):核内像素相对于中心 ( 0 , 0 ) (0,0) (0,0) 的坐标
(2)高斯核权重计算
步骤1:确定 3×3 核坐标
中心为 ( 0 , 0 ) (0,0) (0,0),只需要算 3 种位置(其余位置值相同):
- 中心点: ( 0 , 0 ) (0,0) (0,0)(1 个)
- 相邻点: ( 1 , 0 ) (1,0) (1,0)、 ( 0 , 1 ) (0,1) (0,1)(共 4 个)
- 对角点: ( 1 , 1 ) (1,1) (1,1)(共 4 个)
步骤2:获取原始权重(σ=1)
用高斯公式 G ( x , y ) = 1 2 π e − x 2 + y 2 2 G(x,y)=\frac{1}{2\pi}e^{-\frac{x^2+y^2}{2}} G(x,y)=2π1e−2x2+y2 代入坐标,得到近似值:
- 中心点 ( 0 , 0 ) (0,0) (0,0): x 2 + y 2 = 0 x^2+y^2=0 x2+y2=0 → G ≈ 0.159 G≈0.159 G≈0.159
- 相邻点 ( 1 , 0 ) (1,0) (1,0): x 2 + y 2 = 1 x^2+y^2=1 x2+y2=1 → G ≈ 0.092 G≈0.092 G≈0.092
- 对角点 ( 1 , 1 ) (1,1) (1,1): x 2 + y 2 = 2 x^2+y^2=2 x2+y2=2 → G ≈ 0.059 G≈0.059 G≈0.059
步骤3:计算权重总和
总和 = 0.159 + 4 × 0.092 + 4 × 0.059 ≈ 0.876 总和 = 0.159 + 4×0.092 + 4×0.059 ≈ 0.876 总和=0.159+4×0.092+4×0.059≈0.876
步骤4:归一化(让权重和为 1,避免图像变暗)
每个权重除以总和 0.876 0.876 0.876,取近似值:
- 中心点: 0.159 ÷ 0.876 ≈ 0.256 0.159 ÷ 0.876 ≈ 0.256 0.159÷0.876≈0.256
- 相邻点: 0.092 ÷ 0.876 ≈ 0.129 0.092 ÷ 0.876 ≈ 0.129 0.092÷0.876≈0.129
- 对角点: 0.059 ÷ 0.876 ≈ 0.065 0.059 ÷ 0.876 ≈ 0.065 0.059÷0.876≈0.065
步骤5:最终 3×3 高斯核
0.065 0.129 0.065 0.129 0.256 0.129 0.065 0.129 0.065 \] \\begin{bmatrix} 0.065 \& 0.129 \& 0.065 \\\\ 0.129 \& 0.256 \& 0.129 \\\\ 0.065 \& 0.129 \& 0.065 \\end{bmatrix} 0.0650.1290.0650.1290.2560.1290.0650.1290.065 ##### 4. Python 代码实现高斯滤波 ```python def create_gaussian_kernel(kernel_size=3, sigma=1.0): # 校验核尺寸为奇数 if kernel_size % 2 == 0: raise ValueError("核尺寸必须为奇数,请修改kernel_size参数") # 确定核中心坐标,生成网格坐标 center = kernel_size // 2 x, y = np.meshgrid(np.arange(-center, center+1), np.arange(-center, center+1)) # 实现二维高斯函数公式 gaussian = np.exp(-(x**2 + y**2) / (2 * sigma**2)) / (2 * np.pi * sigma**2) # 归一化处理:保证核权重和为1,避免滤波后图像变暗 gaussian_kernel = gaussian / np.sum(gaussian) return gaussian_kernel ``` * 核尺寸合法性校验 检查输入的核尺寸是否为偶数,若为偶数则抛出 ValueError 异常,因为高斯核必须为奇数尺寸(保证存在唯一中心像素,符合卷积滤波的对称性要求)。 ```python if kernel_size % 2 == 0: raise ValueError("核尺寸必须为奇数,请修改kernel_size参数") ``` * 生成高斯核网格坐标 1. 计算核中心位置:通过整数除法 `kernel_size // 2` 得到核的中心索引 2. 生成网格坐标:利用 `np.meshgrid` 生成二维网格数组 `x` 和 `y`,坐标范围从 `-center` 到 `center`,对应高斯核中每个像素相对于中心像素的坐标偏移 ```python center = kernel_size // 2 x, y = np.meshgrid(np.arange(-center, center+1), np.arange(-center, center+1)) ``` * 实现二维高斯函数计算 按照二维高斯分布的数学公式进行计算,生成未归一化的高斯核矩阵: * 公式核心:`G(x,y) = (1/(2πσ²)) * e^(-(x²+y²)/(2σ²))` * `x² + y²`:计算每个网格点到中心的欧式距离的平方 * `np.exp(...)`:计算指数部分,实现高斯分布的衰减特性 * `1/(2 * np.pi * sigma**2)`:高斯分布的先验归一化系数,保证分布的概率密度特性 ```python gaussian = np.exp(-(x**2 + y**2) / (2 * sigma**2)) / (2 * np.pi * sigma**2) ``` * 高斯核权重归一化处理 将未归一化的高斯核矩阵除以其所有元素的总和,保证高斯核的权重和为 1,避免卷积滤波后图像的整体亮度变暗或过曝,确保滤波仅改变图像的模糊程度,不改变整体明暗。 ```python gaussian_kernel = gaussian / np.sum(gaussian) ``` * 函数返回结果 返回归一化后的二维高斯核矩阵,可直接用于后续的图像卷积滤波操作。 ```python return gaussian_kernel ``` ```python from scipy.signal import convolve2d def manual_gaussian_filter(gray_img, kernel_size=3, sigma=1.0): # 步骤1:生成归一化高斯核 g_kernel = create_gaussian_kernel(kernel_size, sigma) # 步骤2:强制转换为二维灰度图,解决维度异常问题 if gray_img.ndim == 3: gray_img = cv2.cvtColor(gray_img, cv2.COLOR_BGR2GRAY) elif gray_img.ndim != 2: raise ValueError("输入图像仅支持二维灰度图或三维彩色图(自动转灰度)") # 步骤3:二维卷积运算(保持输出尺寸与输入一致,边界填充0) result_img = convolve2d( gray_img, g_kernel, mode='same', boundary='fill', fillvalue=0 ) # 步骤4:裁剪数值范围+转换为uint8,避免溢出/类型异常 result_img = np.clip(result_img, 0, 255) result_img = np.uint8(np.round(result_img)) return result_img ``` * 步骤1:生成归一化高斯核 调用已定义的 `create_gaussian_kernel` 函数,根据输入的核尺寸和标准差,生成符合要求的归一化二维高斯核,为后续卷积运算准备权重模板。 ```python g_kernel = create_gaussian_kernel(kernel_size, sigma) ``` * 步骤2:输入图像维度校验与转换 针对输入图像的维度进行判断和处理,确保后续卷积运算仅作用于二维灰度图: 1. 若输入为3通道彩色图(ndim==3),通过 `cv2.cvtColor` 转换为二维灰度图(BGR格式转灰度格式) 2. 若输入既不是2维也不是3维,抛出 ValueError 异常,明确支持的图像格式 3. 若输入已是2维灰度图,直接保留原始数据,不进行额外处理 ```python if gray_img.ndim == 3: gray_img = cv2.cvtColor(gray_img, cv2.COLOR_BGR2GRAY) elif gray_img.ndim != 2: raise ValueError("输入图像仅支持二维灰度图或三维彩色图(自动转灰度)") ``` * 步骤3:执行二维卷积运算实现高斯滤波 利用 `scipy.signal.convolve2d` 进行二维卷积运算,将高斯核与灰度图像进行卷积,实现图像去噪模糊: * `mode='same'`:保证卷积输出图像的尺寸与输入图像完全一致,便于后续结果对比和处理 * `boundary='fill'`:指定图像边界的填充方式为填充固定值 * `fillvalue=0`:边界填充的固定值为0(黑色填充),解决图像边缘像素无法完整卷积的问题 ```python result_img = convolve2d( gray_img, g_kernel, mode='same', boundary='fill', fillvalue=0 ) ``` * 步骤4:数值范围裁剪与数据类型转换 处理卷积运算后的结果,避免出现数值溢出和数据类型异常,保证图像可正常显示和后续处理: 1. `np.clip(result_img, 0, 255)`:将卷积结果中的数值裁剪到 \[0, 255\] 区间,超出该范围的数值分别强制设为0和255,避免出现过暗或过曝的异常区域 2. `np.round(result_img)`:对卷积结果的浮点数值进行四舍五入,转换为整数型数值,符合图像像素值的整数特性 3. `np.uint8(...)`:将处理后的数值转换为 `uint8` 类型(OpenCV和Matplotlib支持的图像像素类型),得到可直接可视化的灰度图像 ```python result_img = np.clip(result_img, 0, 255) result_img = np.uint8(np.round(result_img)) ``` * 函数返回结果 返回处理完成的去噪灰度图像,该图像为 `uint8` 类型,尺寸与输入图像一致,可直接用于可视化、差异对比等后续操作。 ```python return result_img ``` 全局配置参数(可根据需求修改) ```python img_path = "img/wuhues.jpg" # 图像路径 noise_var = 0.008 # 高斯噪声强度 kernel_3x3 = 3 # 小核尺寸 sigma_3x3 = 1.0 # 小核标准差 kernel_15x15 = 15 # 大核尺寸 sigma_15x15 = 5.0 # 大核标准差 # 读取原始图像(BGR格式,OpenCV默认) img_original_bgr = cv2.imread(img_path) ``` ```python # 生成彩色噪声图像和单独噪声矩阵 img_noisy_bgr, gaussian_noise_color = add_gaussian_noise(img_original_bgr, var=noise_var) # 转换色彩空间(OpenCV BGR → Matplotlib RGB,解决颜色偏差) img_original_rgb = cv2.cvtColor(img_original_bgr, cv2.COLOR_BGR2RGB) img_noisy_rgb = cv2.cvtColor(img_noisy_bgr, cv2.COLOR_BGR2RGB) # 可视化:原始彩色图 + 单独彩色噪声 + 带噪声彩色图 plt.figure(figsize=(18, 6)) # 子图1:原始彩色图像 plt.subplot(1, 3, 1) plt.imshow(img_original_rgb) plt.title("原始彩色图像(无噪声)") plt.axis("off") # 子图2:单独的彩色高斯噪声 plt.subplot(1, 3, 2) plt.imshow(gaussian_noise_color) plt.title("单独的彩色高斯噪声(归一化后)") plt.axis("off") # 子图3:添加噪声后的彩色图像 plt.subplot(1, 3, 3) plt.imshow(img_noisy_rgb) plt.title("添加高斯噪声后的彩色图像") plt.axis("off") plt.tight_layout() plt.show() ```  ```python # 生成3×3和15×15高斯核 gaussian_3x3 = create_gaussian_kernel(kernel_3x3, sigma_3x3) gaussian_15x15 = create_gaussian_kernel(kernel_15x15, sigma_15x15) # 打印高斯核详细信息,验证归一化效果 print("=== 3×3高斯核 ===") print("高精度高斯核:") print(gaussian_3x3) print("\n保留3位小数高斯核:") print(np.round(gaussian_3x3, 3)) print("\n高斯核权重总和(验证是否≈1):", np.sum(gaussian_3x3)) print("\n=== 15×15高斯核 ===") print(f"15×15高斯核权重总和(验证是否≈1):{np.sum(gaussian_15x15):.6f}") ```  ```python # 转换为灰度图并添加高斯噪声 gray_img_original = cv2.cvtColor(img_original_bgr, cv2.COLOR_BGR2GRAY) gray_img_noisy, _ = add_gaussian_noise(gray_img_original, var=noise_var) # 执行手动高斯滤波(3×3小核 + 15×15大核) blur_manual_3x3 = manual_gaussian_filter(gray_img_noisy, kernel_3x3, sigma_3x3) blur_manual_15x15 = manual_gaussian_filter(gray_img_noisy, kernel_15x15, sigma_15x15) ``` * 执行手动高斯滤波(3×3小核 + 15×15大核) 1. 3×3 小核滤波:调用 `manual_gaussian_filter` 函数,以带噪声的灰度图为输入,传入 3×3 核尺寸和对应标准差,执行轻量高斯滤波,保留图像更多细节,仅做轻微去噪 2. 15×15 大核滤波:同样调用 `manual_gaussian_filter` 函数,传入更大的 15×15 核尺寸和对应标准差,执行重度高斯滤波,对图像进行大幅模糊(炸裂效果),去噪效果更强但细节丢失更多 3. 两个滤波结果分别存储,用于后续可视化对比和与 OpenCV 滤波结果的差异分析 ```python # 可视化灰度图滤波结果(2×2布局) plt.figure(figsize=(12, 12)) # 子图1:原始灰度图像 plt.subplot(2, 2, 1) plt.imshow(gray_img_original, cmap="gray") plt.title("原始灰度图像(无噪声)") plt.axis("off") # 子图2:添加噪声后的灰度图像 plt.subplot(2, 2, 2) plt.imshow(gray_img_noisy, cmap="gray") plt.title("添加高斯噪声后的图像") plt.axis("off") # 子图3:3×3小核去噪结果 plt.subplot(2, 2, 3) plt.imshow(blur_manual_3x3, cmap="gray") plt.title("3×3小核去噪(保留细节)") plt.axis("off") # 子图4:15×15大核去噪结果 plt.subplot(2, 2, 4) plt.imshow(blur_manual_15x15, cmap="gray") plt.title("15×15大核去噪(炸裂模糊)") plt.axis("off") plt.tight_layout() plt.show() ```   ```python # 彩色图OpenCV高斯滤波 blur_cv2_3x3 = cv2.GaussianBlur(img_noisy_bgr, (kernel_3x3, kernel_3x3), sigmaX=sigma_3x3) blur_cv2_15x15 = cv2.GaussianBlur(img_noisy_bgr, (kernel_15x15, kernel_15x15), sigmaX=sigma_15x15) # 转换彩色滤波结果为RGB格式(用于Matplotlib可视化) blur_cv2_3x3_rgb = cv2.cvtColor(blur_cv2_3x3, cv2.COLOR_BGR2RGB) blur_cv2_15x15_rgb = cv2.cvtColor(blur_cv2_15x15, cv2.COLOR_BGR2RGB) ``` * 彩色图OpenCV高斯滤波 1. 调用OpenCV内置的`cv2.GaussianBlur`函数,直接对带噪声的BGR格式彩色图进行高斯滤波,无需手动实现卷积,效率更高且优化更完善 2. 第一个参数:输入带噪声的彩色图`img_noisy_bgr` 3. 第二个参数:高斯核尺寸,以元组形式传入`(kernel_size, kernel_size)`,要求宽和高相等且为奇数(与手动实现的高斯核要求一致) 4. 第三个参数`sigmaX`:X方向的高斯标准差,此处传入预设的`sigma_3x3`/`sigma_15x15`,Y方向未指定则默认与X方向相等 5. 分别执行3×3小核和15×15大核滤波,得到对应的彩色模糊图像 * 转换彩色滤波结果为RGB格式(用于Matplotlib可视化) 1. OpenCV默认读取和处理的彩色图为BGR格式,而Matplotlib可视化时识别的是RGB格式,直接显示BGR图会出现颜色偏差 2. 调用`cv2.cvtColor`函数,传入转换标识`cv2.COLOR_BGR2RGB`,将OpenCV滤波后的BGR格式图像转换为RGB格式 3. 转换后的结果用于后续Matplotlib的图像展示,保证颜色显示正常 ```python # 可视化彩色图滤波结果(2×2布局) plt.figure(figsize=(12, 12)) # 子图1:原始彩色图像 plt.subplot(2, 2, 1) plt.imshow(img_original_rgb) plt.title("原始彩色图像(无噪声)") plt.axis("off") # 子图2:添加噪声后的彩色图像 plt.subplot(2, 2, 2) plt.imshow(img_noisy_rgb) plt.title("添加高斯噪声后的彩色图像") plt.axis("off") # 子图3:3×3小核OpenCV去噪结果 plt.subplot(2, 2, 3) plt.imshow(blur_cv2_3x3_rgb) plt.title("3×3小核去噪(保留细节)") plt.axis("off") # 子图4:15×15大核OpenCV去噪结果 plt.subplot(2, 2, 4) plt.imshow(blur_cv2_15x15_rgb) plt.title("15×15大核强去噪(全模糊)") plt.axis("off") plt.tight_layout() plt.show() ```   ```python # 灰度图OpenCV高斯滤波(用于后续差异对比) blur_cv2_gray_3x3 = cv2.GaussianBlur(gray_img_noisy, (kernel_3x3, kernel_3x3), sigmaX=sigma_3x3) blur_cv2_gray_15x15 = cv2.GaussianBlur(gray_img_noisy, (kernel_15x15, kernel_15x15), sigmaX=sigma_15x15) # 统一数据类型+裁剪数值范围,解决差异值异常问题 blur_manual_3x3 = np.uint8(np.clip(blur_manual_3x3, 0, 255)) blur_cv2_gray_3x3 = np.uint8(np.clip(blur_cv2_gray_3x3, 0, 255)) blur_manual_15x15 = np.uint8(np.clip(blur_manual_15x15, 0, 255)) blur_cv2_gray_15x15 = np.uint8(np.clip(blur_cv2_gray_15x15, 0, 255)) # 计算像素差异 diff_3x3 = np.abs(blur_manual_3x3 - blur_cv2_gray_3x3) max_diff_3x3 = np.max(diff_3x3) mean_diff_3x3 = np.mean(diff_3x3) diff_15x15 = np.abs(blur_manual_15x15 - blur_cv2_gray_15x15) max_diff_15x15 = np.max(diff_15x15) mean_diff_15x15 = np.mean(diff_15x15) # 打印量化差异结果 print("=== 3×3小核 手动实现 vs OpenCV封装函数 去噪结果对比 ===") print(f"像素差异最大值:{max_diff_3x3}") print(f"像素差异平均值:{mean_diff_3x3:.4f}") print("\n=== 15×15大核(炸裂效果) 手动实现 vs OpenCV封装函数 去噪结果对比 ===") print(f"像素差异最大值:{max_diff_15x15}") print(f"像素差异平均值:{mean_diff_15x15:.4f}") ``` * 灰度图OpenCV高斯滤波(用于后续差异对比) 1. 针对带噪声的灰度图`gray_img_noisy`执行OpenCV内置高斯滤波,与手动实现的灰度图滤波保持输入、核尺寸、标准差一致,确保差异对比的公平性和有效性 2. 调用`cv2.GaussianBlur`函数,输入二维灰度图,核尺寸以元组`(kernel_size, kernel_size)`传入,`sigmaX`指定对应标准差,得到OpenCV优化后的灰度滤波结果 3. 分别生成3×3和15×15核的滤波结果,用于后续与手动滤波结果逐一对比 ```python blur_cv2_gray_3x3 = cv2.GaussianBlur(gray_img_noisy, (kernel_3x3, kernel_3x3), sigmaX=sigma_3x3) blur_cv2_gray_15x15 = cv2.GaussianBlur(gray_img_noisy, (kernel_15x15, kernel_15x15), sigmaX=sigma_15x15) ``` * 统一数据类型+裁剪数值范围,解决差异值异常问题 1. `np.clip(..., 0, 255)`:将滤波结果中的数值裁剪到\[0, 255\]合法像素区间,消除卷积运算或OpenCV内部优化带来的数值溢出(小于0或大于255)问题 2. `np.uint8(...)`:将所有滤波结果统一转换为`uint8`数据类型,避免手动实现与OpenCV实现的数据类型不匹配(如`float32`与`uint8`)导致的差异计算异常 3. 对4个滤波结果(3×3手动/OpenCV、15×15手动/OpenCV)统一处理,保证后续像素差异计算的准确性 ```python blur_manual_3x3 = np.uint8(np.clip(blur_manual_3x3, 0, 255)) blur_cv2_gray_3x3 = np.uint8(np.clip(blur_cv2_gray_3x3, 0, 255)) blur_manual_15x15 = np.uint8(np.clip(blur_manual_15x15, 0, 255)) blur_cv2_gray_15x15 = np.uint8(np.clip(blur_cv2_gray_15x15, 0, 255)) ``` * 计算像素差异 1. `np.abs(...)`:计算手动滤波与OpenCV滤波结果对应像素值的绝对差,得到差异矩阵,消除正负差值相互抵消的问题 2. `np.max(...)`:提取差异矩阵中的最大值,反映两种实现方式的最大像素偏差 3. `np.mean(...)`:计算差异矩阵的平均值,反映两种实现方式的整体像素偏差水平 4. 分别计算3×3核和15×15核对应的差异矩阵、最大值、平均值,为量化对比提供数据支撑 ```python diff_3x3 = np.abs(blur_manual_3x3 - blur_cv2_gray_3x3) max_diff_3x3 = np.max(diff_3x3) mean_diff_3x3 = np.mean(diff_3x3) diff_15x15 = np.abs(blur_manual_15x15 - blur_cv2_gray_15x15) max_diff_15x15 = np.max(diff_15x15) mean_diff_15x15 = np.mean(diff_15x15) ```  ```python plt.figure(figsize=(12, 12)) # 子图1:3×3手动去噪结果 plt.subplot(2, 2, 1) plt.imshow(blur_manual_3x3, cmap="gray") plt.title("3×3手动实现去噪结果") plt.axis("off") # 子图2:15×15手动去噪结果 plt.subplot(2, 2, 2) plt.imshow(blur_manual_15x15, cmap="gray") plt.title("15×15手动实现去噪(炸裂效果)") plt.axis("off") # 子图3:3×3差异图 plt.subplot(2, 2, 3) plt.imshow(diff_3x3, cmap="gray", vmin=0, vmax=np.min([max_diff_3x3, 50])) plt.title(f"3×3去噪结果差异图(最大值:{max_diff_3x3})") plt.axis("off") # 子图4:15×15差异图 plt.subplot(2, 2, 4) plt.imshow(diff_15x15, cmap="gray", vmin=0, vmax=np.min([max_diff_15x15, 50])) plt.title(f"15×15去噪结果差异图(最大值:{max_diff_15x15})") plt.axis("off") plt.tight_layout() plt.show() ```   ##### 5.cv2.GaussianBlur()函数 `cv2.GaussianBlur()` 是 OpenCV 库中专门用于实现「高斯滤波」的内置函数,核心作用是对图像进行高斯模糊去噪,同时最大程度保留图像的边缘细节(相比均值滤波更柔和、细节丢失更少),底层采用 C++ 优化实现,运行高效,是图像处理中抑制高斯噪声、平滑图像的核心工具。 ```python dst = cv2.GaussianBlur(src, ksize, sigmaX, sigmaY=None, borderType=None) ``` 核心必选参数(实际开发中最常用) | 参数 | 含义与说明 | |----------|-------------------------------------------------------------------------------------------------------| | `src` | 输入图像(待滤波的图像),支持 uint8、float32 等数据类型,OpenCV 读取的灰度图 / BGR 彩色图均可直接传入,彩色图会对每个通道独立进行高斯滤波。 | | `ksize` | 高斯核尺寸,格式为 (width, height)(宽度 × 高度),要求为正奇数且宽高相等(常用:(3, 3)、(5, 5)、(15, 15)),核尺寸越大,模糊 / 去噪效果越强,图像细节丢失越多。 | | `sigmaX` | X 方向的高斯标准差,控制高斯分布的离散程度(即模糊程度),与核尺寸配套使用;若设置为 0,OpenCV 会自动根据核尺寸计算对应的最优标准差,推荐手动指定以精准控制模糊效果。 | 可选参数(默认值满足常规需求) | 参数 | 含义与说明 | |--------------|---------------------------------------------------------------------------------------------| | `sigmaY` | Y 方向的高斯标准差,默认值为 None(等价于 0),此时与 `sigmaX` 取值相等,实现「各向同性高斯滤波」;若需实现「各向异性高斯滤波」(如仅横向模糊),可单独设置非零值。 | | `borderType` | 图像边界填充方式,默认值为 cv2.BORDER_DEFAULT,采用边缘插值填充方式解决图像边缘无法提取完整高斯核的问题,减少边缘像素的滤波失真,优于固定值填充。 | 返回值 `dst` 滤波后的输出图像,格式、尺寸与输入图像 `src` 完全一致: * 输入灰度图,返回二维灰度图;输入 BGR 彩色图,返回 BGR 格式彩色图,各通道独立完成滤波且颜色信息保持一致。 * 像素值已完成高斯加权平均更新,保留 OpenCV 默认的 uint8 图像格式,可直接用于后续的图像裁剪、边缘检测等其他 OpenCV 处理流程。 这时我们就可以对上面的代码进行优化 ```python # 读取原始图像(OpenCV默认BGR格式) img = cv2.imread("img/wuhues.jpg") # BGR 转 RGB(适配Matplotlib可视化,解决颜色偏差问题) img_rgb = cv2.cvtColor(img, cv2.COLOR_BGR2RGB) # 为图像添加高斯噪声(模拟真实场景中的噪声干扰) np.random.seed(42) noise = np.random.normal(0, 0.05, img.shape).astype(np.float32) img_float = img.astype(np.float32) / 255.0 noisy_img_float = img_float + noise noisy_img = np.clip(noisy_img_float * 255.0, 0, 255).astype(np.uint8) noisy_img_rgb = cv2.cvtColor(noisy_img, cv2.COLOR_BGR2RGB) # 执行OpenCV高斯滤波(两种核尺寸对比) # 3×3 小核高斯滤波(轻量模糊,保留更多细节) filtered_img_3 = cv2.GaussianBlur(noisy_img, ksize=(3, 3), sigmaX=1.0) filtered_img_3_rgb = cv2.cvtColor(filtered_img_3, cv2.COLOR_BGR2RGB) # 15×15 大核高斯滤波(重度模糊,强去噪效果) filtered_img_15 = cv2.GaussianBlur(noisy_img, ksize=(15, 15), sigmaX=5.0) filtered_img_15_rgb = cv2.cvtColor(filtered_img_15, cv2.COLOR_BGR2RGB) ``` * 先通过`cv2.imread()`读取原始图像,再通过`cv2.cvtColor()`转换为 RGB 格式,为后续 Matplotlib 可视化做准备; * 接着通过`np.random.normal()`生成高斯噪声,将图像转换为浮点型后叠加噪声,再裁剪回 uint8 格式,得到带噪图像且避免数值溢出; * 最后通过核心函数`cv2.GaussianBlur()`分别以 3×3/15×15 核尺寸执行高斯滤波,再转换为 RGB 格式,实现「图像读取→格式适配→噪声添加→高斯滤波→可视化适配」的完整流程; * 小核与大核滤波结果形成对比,便于后续观察不同模糊程度的去噪效果和细节保留情况。 ```python plt.figure(figsize=(16, 12)) plt.subplot(2, 2, 1) plt.imshow(img_rgb) plt.title("原始彩色图像", fontsize=12) plt.axis('off') plt.subplot(2, 2, 2) plt.imshow(noisy_img_rgb) plt.title("添加高斯噪声后的图像", fontsize=12) plt.axis('off') plt.subplot(2, 2, 3) plt.imshow(filtered_img_3_rgb) plt.title("OpenCV 3×3 高斯滤波结果(轻量模糊)", fontsize=12) plt.axis('off') plt.subplot(2, 2, 4) plt.imshow(filtered_img_15_rgb) plt.title("OpenCV 15×15 高斯滤波结果(重度模糊)", fontsize=12) plt.axis('off') plt.tight_layout() plt.show() ```  ##### 6. 总结 1. 高斯滤波主要解决图像中的**高斯噪声** (又称**正态噪声**)干扰问题,同时可实现图像平滑处理,相较于均值滤波更能保留图像边缘细节,减少边缘模糊失真。 2. 高斯滤波的核心逻辑是 **「高斯核加权 + 滑动窗口卷积」**,通过构建符合二维高斯分布的归一化权重核,对邻域像素进行不等权加权求和,核心权重集中在窗口中心,向四周指数衰减。 3. 高斯滤波的数学本质是 **「二维高斯分布的邻域加权平均计算」** ,通过 G ( x , y ) = 1 2 π σ 2 e − x 2 + y 2 2 σ 2 G(x,y) = \\frac{1}{2\\pi\\sigma\^2} e\^{-\\frac{x\^2 + y\^2}{2\\sigma\^2}} G(x,y)=2πσ21e−2σ2x2+y2 构建权重分布,归一化后避免图像明暗变化,最终通过卷积运算实现噪声抵消和图像平滑,工程中可通过 `cv2.GaussianBlur()` 快速落地。 #### 均值滤波 vs 高斯滤波(处理高斯噪声)对比表 | 对比维度 | 均值滤波(`cv2.blur`) | 高斯滤波(`cv2.GaussianBlur`) | |:------------|:------------------------------|:------------------------------------------------------------| | 能否处理高斯噪声 | 可以(有基础抑制效果) | 可以(抑制效果更优,处理高斯噪声首选) | | 核心计算逻辑 | 邻域内等权重算术平均,所有像素权重完全一致,无优先级区分 | 邻域内加权平均,权重服从二维高斯分布(钟形曲线),近大远小(中心像素权重最高,越边缘权重越低) | | 对高斯噪声匹配度 | 一般(无针对性,仅通过平均压制随机像素波动) | 极高("高斯对高斯",数学上高度匹配,去噪更彻底且更柔和) | | 边缘/细节保留能力 | 差(严重模糊图像边缘、纹理细节,滤波核越大模糊越明显) | 好(加权平均逻辑更贴合图像像素分布,更好保留边缘和纹理,模糊程度更柔和) | | OpenCV 实现函数 | `cv2.blur()` | `cv2.GaussianBlur()` | | 核心参数 | 滤波核大小(如 `(3,3)`、`(5,5)`,奇数为宜) | 1. 滤波核大小(必须为奇数,如 `(5,5)`);2. `sigmaX`(X方向高斯标准差,设为0时自动适配核大小) | | 相同核大小模糊程度 | 较重,整体偏糊,细节丢失较多 | 较轻,视觉效果更自然,细节保留更完整 | | 适用场景 | 对图像细节要求不高的简单去噪场景,快速压制噪声 | 对图像细节要求较高的高斯噪声去噪场景,是处理高斯噪声的主流首选方案 | ### Ⅲ、非线性滤波 #### 三、中值滤波(Median Filter) ##### 1. 椒盐噪声 1. 定义:椒盐噪声(又称脉冲噪声)是数字图像中最常见的噪声类型之一,因噪声表现为图像上随机分布的白色亮点(盐噪声)和黑色暗点(椒噪声),类似撒了一层盐和黑胡椒而得名。 2. 像素值特征(针对8位灰度/彩色图像,像素值范围0-255): * 盐噪声(Salt Noise):对应像素极端高值,通常赋值为255(纯白色),模拟图像中的亮斑干扰; * 椒噪声(Pepper Noise):对应像素极端低值,通常赋值为0(纯黑色),模拟图像中的暗斑干扰。 3. 常见产生原因: * 图像采集阶段:传感器受电磁干扰、光线突变、设备硬件故障; * 图像传输阶段:网络信号丢失、数据传输错误; * 图像存储阶段:存储介质损坏、文件格式异常。 4. 核心特点: * 噪声为离散孤立点,不连续分布,无规律可循; * 噪声像素值与正常像素值差异显著,易与图像内容区分; * 可控制总噪声比例,通常盐噪声和椒噪声各占一半,避免图像整体明暗偏移; * 对图像视觉效果影响大,严重时会掩盖图像细节,干扰后续图像分析(如边缘检测、目标识别) > 椒盐噪声的实现核心是生成随机噪声掩码,通过掩码定位噪声像素并赋值,主要分为两种场景:给原始图像叠加噪声、生成独立的纯噪声图。 给原始图像叠加椒盐噪声 ```python def add_salt_pepper_noise(image, prob=0.05): output = np.copy(image) h, w = image.shape[:2] single_prob = prob / 2 # 单种噪声比例(盐、椒各占一半) noise_mask = np.random.rand(h, w) # 统一噪声掩码,避免叠加 # 盐噪声(白色) output[noise_mask < single_prob] = 255 # 椒噪声(黑色) output[noise_mask > 1 - single_prob] = 0 return output ``` ##### 2. 中值滤波器核心概述 中值滤波是一种**基于像素值排序统计** 的非线性平滑滤波,常用于**消除椒盐噪声** (如图像中的黑白斑点、传输过程中的脉冲干扰)。 它的核心特点是:对图像滑动窗口内的所有像素按灰度值排序,取**中间值**作为窗口中心点像素的新值,既能有效去除脉冲噪声,又能较好地保留图像边缘细节(无加权平均带来的模糊失真)。  ##### 3. 中值滤波的数学原理 ###### (1)核心数学表达式 中值滤波的核心是**中值运算** ,数学上用**中位数函数 m e d ( ⋅ ) med(\\cdot) med(⋅)** 表示,对于尺寸为 n × n n×n n×n( n n n 为奇数)的滑动窗口,其数学表达式为: g ( x , y ) = m e d { f ( x + i , y + j ) ∣ ( i , j ) ∈ W } g(x,y) = med\\left\\{ f(x+i, y+j) \\mid (i,j) \\in W \\right\\} g(x,y)=med{f(x+i,y+j)∣(i,j)∈W} 其中各参数含义: * g ( x , y ) g(x,y) g(x,y):中值滤波后,图像在 ( x , y ) (x,y) (x,y) 坐标(窗口中心点)的像素灰度值; * f ( x + i , y + j ) f(x+i, y+j) f(x+i,y+j):原始图像在滑动窗口内的像素灰度值, ( x , y ) (x,y) (x,y) 为窗口中心点; * W W W: n × n n×n n×n 大小的滑动窗口(如 3×3、5×5), ( i , j ) (i,j) (i,j) 为窗口内像素相对于中心点的坐标偏移量(如 3×3 窗口中, i , j ∈ { − 1 , 0 , 1 } i,j \\in \\{-1,0,1\\} i,j∈{−1,0,1}); * m e d ( ⋅ ) med(\\cdot) med(⋅):中位数函数,对输入的一组像素值进行排序后,返回中间位置的数值。 * a 1 , a 2 , . . . , a N a_1, a_2, ..., a_N a1,a2,...,aN:窗口内按升序排序后的像素灰度值; * N N N:窗口内像素总数(如 3×3 窗口 N = 9 N=9 N=9,5×5 窗口 N = 25 N=25 N=25)。 > 灰度值:用来表示**灰度图像单个像素明暗程度的数值** ,灰度图无色彩,仅靠灰度值呈现内容。 > > 常用取值范围(uint8格式):**0 \~ 255** > > * 0:纯黑色(最暗) > * 255:纯白色(最亮) > * 中间值:不同深浅的灰色,数值越大越亮。 > 与彩色图的关系:彩色图可通过公式转换为灰度图,最终每个像素浓缩为一个灰度值(简化图像处理)。 > 核心作用:作为图像处理(滤波、边缘检测等)的基础,降低计算复杂度。 > 补充:对于窗口内像素总数 N N N( N = n 2 N=n\^2 N=n2, n n n 为奇数),排序后中间值的位置为第 N + 1 2 \\frac{N+1}{2} 2N+1 位(从 1 开始计数),对应数学表达式可细化为: > m e d { a 1 , a 2 , . . . , a N } = a N + 1 2 ( 其中 a 1 ≤ a 2 ≤ . . . ≤ a N ) med\\left\\{ a_1, a_2, ..., a_N \\right\\} = a_{\\frac{N+1}{2}} \\quad (其中\\ a_1 \\le a_2 \\le ... \\le a_N) med{a1,a2,...,aN}=a2N+1(其中 a1≤a2≤...≤aN) ###### (2)3×3 中值滤波分步实现 步骤1:确定 3×3 滑动窗口及像素值 假设图像中某一 3×3 窗口内的像素灰度值如下(模拟含椒盐噪声的区域,黑白斑点为极端值): \[ 12 15 13 14 255 16 11 17 18 \] \\begin{bmatrix} 12 \& 15 \& 13 \\\\ 14 \& 255 \& 16 \\\\ 11 \& 17 \& 18 \\end{bmatrix} 1214111525517131618 * 窗口内存在椒盐噪声:255(白斑,极端高值),其余为正常图像灰度值(10\~20 之间); * 3×3 窗口像素总数 N = 9 N=9 N=9(奇数),根据公式,排序后取第 9 + 1 2 = 5 \\frac{9+1}{2}=5 29+1=5 个值作为中间值。 步骤2:对窗口内像素值进行升序排序 将 3×3 窗口内的 9 个像素值提取出来,按从小到大的顺序排列,得到有序数组 a 1 ≤ a 2 ≤ . . . ≤ a 9 a_1 \\le a_2 \\le ... \\le a_9 a1≤a2≤...≤a9: \[ 11 , 12 , 13 , 14 , 15 , 16 , 17 , 18 , 255 \] \[11, 12, 13, 14, 15, 16, 17, 18, 255\] \[11,12,13,14,15,16,17,18,255
- 排序后极端值(255)被排至末尾,正常灰度值集中在前面,有效分离噪声与正常像素;
- 排序是中值滤波的核心步骤,为后续提取中间值提供基础。
步骤3:提取中间值(代入数学公式)
根据中值运算的数学表达式,取排序后第 5 个值( a 5 a_5 a5)作为中间值:
m e d { 11 , 12 , 13 , 14 , 15 , 16 , 17 , 18 , 255 } = a 5 = 15 med\left\{ 11,12,13,14,15,16,17,18,255 \right\} = a_5 = 15 med{11,12,13,14,15,16,17,18,255}=a5=15
- 本次窗口的中间值为:15,该值为窗口内正常像素的典型灰度值,无噪声干扰。
步骤4:替换窗口中心点像素值
将 3×3 窗口中心点的原像素值(255,椒盐噪声)替换为提取的中间值(15),替换后窗口像素值更新为:
12 15 13 14 15 16 11 17 18 \] \\begin{bmatrix} 12 \& 15 \& 13 \\\\ 14 \& 15 \& 16 \\\\ 11 \& 17 \& 18 \\end{bmatrix} 121411151517131618 * 替换后椒盐噪声(255)被消除,窗口内像素值恢复为正常范围,无明显灰度值突变; * 窗口中心点周围的像素值未发生变化,保留了图像的边缘和纹理细节。 步骤5:滑动窗口遍历整个图像 将 3×3 窗口按从左到右、从上到下的顺序遍历整个图像,对每个窗口重复"排序→代入公式取中间值→替换中心点"的操作,最终得到完整的中值滤波处理图像。 ###### (3)5×5 中值滤波补充说明 对于 5×5 更大尺寸的窗口(像素总数 N = 25 N=25 N=25),核心数学逻辑与 3×3 窗口一致: 1. 提取 5×5 窗口内的 25 个像素灰度值,组成原始数据组; 2. 对 25 个像素值进行升序排序,得到有序数组 a 1 ≤ a 2 ≤ . . . ≤ a 25 a_1 \\le a_2 \\le ... \\le a_{25} a1≤a2≤...≤a25; 3. 代入中值公式,取排序后第 25 + 1 2 = 13 \\frac{25+1}{2}=13 225+1=13 个值( a 13 a_{13} a13)作为中间值; 4. 替换窗口中心点像素值,滑动遍历整个图像; 5. 特点:窗口尺寸越大,降噪效果越强,但图像细节保留程度略有下降,运行速度也会变慢。 ##### 4. Python 代码实现中值滤波 ```python # 转换为RGB格式(用于matplotlib正确显示,OpenCV默认读取为BGR) img_rgb = cv2.cvtColor(img, cv2.COLOR_BGR2RGB) # 2. 给图像添加椒盐噪声(提高噪声比例,更易观察去噪效果) noisy_img = add_salt_pepper_noise(img, prob=0.08) noisy_img_rgb = cv2.cvtColor(noisy_img, cv2.COLOR_BGR2RGB) # 3. 中值滤波去噪(两种窗口尺寸对比) ## 3.1 3×3窗口中值滤波(细节保留最优) median_filter_3x3 = cv2.medianBlur(noisy_img, 3) # 第二个参数为窗口尺寸,必须为奇数 median_3x3_rgb = cv2.cvtColor(median_filter_3x3, cv2.COLOR_BGR2RGB) ## 3.2 5×5窗口中值滤波(去噪效果更强,轻微模糊) median_filter_5x5 = cv2.medianBlur(noisy_img, 5) median_5x5_rgb = cv2.cvtColor(median_filter_5x5, cv2.COLOR_BGR2RGB) ``` `add_salt_pepper_noise(img, prob=0.08):`调用自定义的椒盐噪声添加函数,给原始 BGR 图像叠加总比例为 8% 的椒盐噪声(其中盐噪声 \<白色,255\>、椒噪声 \< 黑色,0 \> 各占 4%),返回带噪声的 BGR 格式图像。 3×3 窗口中值滤波(细节保留最优) ```python median_filter_3x3 = cv2.medianBlur(noisy_img, 3) ``` * 利用非线性滤波消除椒盐噪声,同时最大程度保留图像边缘和纹理细节。 5×5 窗口中值滤波(去噪效果更强,轻微模糊) ```python median_filter_5x5 = cv2.medianBlur(noisy_img, 5) ``` * 更强力消除密集 / 连续椒盐噪声,适用于重度噪声场景。 ```python plt.figure(figsize=(12, 12)) # 子图1:原始图像 plt.subplot(2, 2, 1) plt.imshow(img_rgb) plt.title("1. 原始图像") plt.axis("off") # 子图2:添加椒盐噪声后的图像 plt.subplot(2, 2, 2) plt.imshow(noisy_img_rgb) plt.title("2. 添加椒盐噪声后的图像(8%噪声比例)") plt.axis("off") # 子图3:3×3窗口中值滤波去噪结果 plt.subplot(2, 2, 3) plt.imshow(median_3x3_rgb) plt.title("3. 3×3 中值滤波去噪结果(细节保留最优)") plt.axis("off") # 子图4:5×5窗口中值滤波去噪结果 plt.subplot(2, 2, 4) plt.imshow(median_5x5_rgb) plt.title("4. 5×5 中值滤波去噪结果(去噪更强,轻微模糊)") plt.axis("off") # 自动调整子图间距,避免重叠 plt.tight_layout() # 显示图像 plt.show() ```   ##### 5. cv2.medianBlur() 函数 ```python cv2.medianBlur(src, ksize) ``` * 核心作用:实现中值滤波(非线性滤波),高效消除椒盐噪声,同时尽可能保留图像边缘细节。 * 关键说明:ksize 为窗口尺寸(必须为奇数),窗口越大去噪能力越强,图像轻微模糊感也越明显。 ##### 6.总结 中值滤波属于非线性滤波,区别于均值、高斯滤波的线性加权求和。 > 核心逻辑是「**滑动窗口遍历→像素排序→取中值替换窗口中心点」**。 核心优势:对 **椒盐噪声(脉冲噪声) 具有近乎 "根治" 的效果**,去噪过程中能最大程度保留图像的边缘、纹理等细节,无明显边缘模糊失真。 关键参数(窗口尺寸):窗口尺寸需为奇数(3×3、5×5 为主),3×3 窗口优先选择(保细节、无明显模糊),5×5 窗口适用于密集 / 重度椒盐噪声(去噪更强,但伴随轻微模糊)。 #### 四、双边滤波(Bilateral Filter) ##### 1. 双边滤波器核心概述 双边滤波是一种非线性滤波,兼具「噪声去除」和「边缘保留」的双重优势,解决了传统高斯滤波等线性滤波去噪同时模糊边缘的痛点  ##### 2. 双边滤波的数学原理 ###### (1)核心数学表达式 双边滤波的核心是**双重高斯加权求和运算** ,属于非线性加权平均滤波,数学上通过**空间高斯核** 和**值域高斯核** 的乘积实现权重分配,对于图像中任意像素点 ( x , y ) (x,y) (x,y),其数学表达式为: g ( x , y ) = 1 W p ( x , y ) ∑ ( i , j ) ∈ Ω f ( i , j ) ⋅ G s ( ∥ ( x , y ) − ( i , j ) ∥ ) ⋅ G r ( ∣ f ( x , y ) − f ( i , j ) ∣ ) g(x,y) = \\frac{1}{W_{p}(x,y)} \\sum_{(i,j) \\in \\Omega} f(i,j) \\cdot G_s(\\\|(x,y)-(i,j)\\\|) \\cdot G_r(\|f(x,y)-f(i,j)\|) g(x,y)=Wp(x,y)1(i,j)∈Ω∑f(i,j)⋅Gs(∥(x,y)−(i,j)∥)⋅Gr(∣f(x,y)−f(i,j)∣) 其中各参数含义: * g ( x , y ) g(x,y) g(x,y):双边滤波后,图像在 ( x , y ) (x,y) (x,y) 坐标的像素灰度值/颜色值; * f ( i , j ) f(i,j) f(i,j):原始图像在邻域窗口内 ( i , j ) (i,j) (i,j) 坐标的像素灰度值/颜色值; * Ω \\Omega Ω:以 ( x , y ) (x,y) (x,y) 为中心的邻域窗口(如直径为9的圆形窗口、3×3/5×5矩形窗口); * W p ( x , y ) W_{p}(x,y) Wp(x,y):归一化权重系数(保证滤波后像素值在合理范围),其表达式为 W p ( x , y ) = ∑ ( i , j ) ∈ Ω G s ( ∥ ( x , y ) − ( i , j ) ∥ ) ⋅ G r ( ∣ f ( x , y ) − f ( i , j ) ∣ ) W_{p}(x,y) = \\sum_{(i,j) \\in \\Omega} G_s(\\\|(x,y)-(i,j)\\\|) \\cdot G_r(\|f(x,y)-f(i,j)\|) Wp(x,y)=(i,j)∈Ω∑Gs(∥(x,y)−(i,j)∥)⋅Gr(∣f(x,y)−f(i,j)∣) * G s ( ⋅ ) G_s(\\cdot) Gs(⋅):**空间距离高斯核**(简称空间核),衡量邻域像素与中心点的空间位置差异; * G r ( ⋅ ) G_r(\\cdot) Gr(⋅):**像素值相似性高斯核**(简称值域核),衡量邻域像素与中心点的灰度/颜色值差异; * ∥ ( x , y ) − ( i , j ) ∥ \\\|(x,y)-(i,j)\\\| ∥(x,y)−(i,j)∥:邻域像素 ( i , j ) (i,j) (i,j) 与中心点 ( x , y ) (x,y) (x,y) 的欧几里得距离(空间距离); * ∣ f ( x , y ) − f ( i , j ) ∣ \|f(x,y)-f(i,j)\| ∣f(x,y)−f(i,j)∣:邻域像素 ( i , j ) (i,j) (i,j) 与中心点 ( x , y ) (x,y) (x,y) 的像素值绝对差(灰度/颜色差异)。 > 补充:高斯核(正态分布核)的通用表达式为 G ( t ) = 1 2 π σ e − t 2 2 σ 2 G(t) = \\frac{1}{\\sqrt{2\\pi}\\sigma} e\^{-\\frac{t\^2}{2\\sigma\^2}} G(t)=2π σ1e−2σ2t2,其中 σ \\sigma σ 为标准差,决定高斯核的衰减速度。 > > 1. 空间高斯核 G s G_s Gs 对应的标准差为 σ s \\sigma_s σs(对应OpenCV中`sigmaSpace`),空间距离越远, G s G_s Gs 权重衰减越快; > 2. 值域高斯核 G r G_r Gr 对应的标准差为 σ r \\sigma_r σr(对应OpenCV中`sigmaColor`),像素值差异越大, G r G_r Gr 权重衰减越快; > 3. 双边滤波的最终权重是 G s × G r G_s \\times G_r Gs×Gr,只有"空间距离近**且**像素值相似"的像素,才会获得较高权重。 进一步细化两个核心高斯核的数学表达式: 1. **空间高斯核(衡量空间距离)** G s ( d ) = 1 2 π σ s 2 e − d 2 2 σ s 2 G_s(d) = \\frac{1}{2\\pi\\sigma_s\^2} e\^{-\\frac{d\^2}{2\\sigma_s\^2}} Gs(d)=2πσs21e−2σs2d2 其中 d = ∥ ( x , y ) − ( i , j ) ∥ d = \\\|(x,y)-(i,j)\\\| d=∥(x,y)−(i,j)∥ 为空间欧几里得距离,对于二维图像, d 2 = ( x − i ) 2 + ( y − j ) 2 d\^2 = (x-i)\^2 + (y-j)\^2 d2=(x−i)2+(y−j)2。 2. **值域高斯核(衡量像素值差异)** G r ( Δ ) = 1 2 π σ r 2 e − Δ 2 2 σ r 2 G_r(\\Delta) = \\frac{1}{2\\pi\\sigma_r\^2} e\^{-\\frac{\\Delta\^2}{2\\sigma_r\^2}} Gr(Δ)=2πσr21e−2σr2Δ2 其中 Δ = ∣ f ( x , y ) − f ( i , j ) ∣ \\Delta = \|f(x,y)-f(i,j)\| Δ=∣f(x,y)−f(i,j)∣ 为像素值绝对差,灰度图中为单个灰度值的差异,彩色图中为各通道颜色值差异的综合。 ###### (2)3×3 双边滤波分步实现 步骤1:确定 3×3 邻域窗口及像素值 假设图像中某一 3×3 窗口内的像素灰度值如下(模拟含高斯噪声的边缘区域,左侧为暗区、右侧为亮区,边缘清晰): \[ 22 25 180 20 24 185 23 26 178 \] \\begin{bmatrix} 22 \& 25 \& 180 \\\\ 20 \& 24 \& 185 \\\\ 23 \& 26 \& 178 \\end{bmatrix} 222023252426180185178 * 窗口内存在**高斯噪声** (如22略偏离24、180略偏离185),同时存在明显边缘(左侧20~26,右侧178~185,像素值突变); * 窗口中心点为 ( x , y ) (x,y) (x,y),对应像素值 f ( x , y ) = 24 f(x,y)=24 f(x,y)=24,邻域窗口 Ω \\Omega Ω 包含9个像素, ( i , j ) (i,j) (i,j) 为窗口内像素相对于中心点的坐标偏移量( i , j ∈ { − 1 , 0 , 1 } i,j \\in \\{-1,0,1\\} i,j∈{−1,0,1}); * 设定滤波参数:空间标准差 σ s = 1.0 \\sigma_s=1.0 σs=1.0,值域标准差 σ r = 10.0 \\sigma_r=10.0 σr=10.0(经验值,保证边缘保留效果)。 步骤2:计算每个邻域像素的双重高斯权重 **双边滤波的每一个权重 Wi,j,都是 "邻域像素 (i,j) 相对于中心点 (x,y) 的空间距离" 和 "像素值差异" 共同决定的** 对窗口内每个像素 ( i , j ) (i,j) (i,j),分别计算空间高斯权重 G s G_s Gs、值域高斯权重 G r G_r Gr,最终权重 W = G s × G r W=G_s \\times G_r W=Gs×Gr,以3个典型像素为例(其余像素同理): 1. 中心点像素 ( x , y ) (x,y) (x,y)(值=24): * 空间距离 d = 0 d=0 d=0,代入 G s G_s Gs 得 G s = e − 0 2 2 × 1.0 2 = 1.0 G_s=e\^{-\\frac{0\^2}{2×1.0\^2}}=1.0 Gs=e−2×1.0202=1.0; * 像素值差异 Δ = ∣ 24 − 24 ∣ = 0 \\Delta=\|24-24\|=0 Δ=∣24−24∣=0,代入 G r G_r Gr 得 G r = e − 0 2 2 × 10.0 2 = 1.0 G_r=e\^{-\\frac{0\^2}{2×10.0\^2}}=1.0 Gr=e−2×10.0202=1.0; * 最终权重 W = 1.0 × 1.0 = 1.0 W=1.0×1.0=1.0 W=1.0×1.0=1.0。 2. 左侧邻域像素 ( x − 1 , y ) (x-1,y) (x−1,y)(值=20): * 空间距离 d = ( − 1 ) 2 + 0 2 = 1 d=\\sqrt{(-1)\^2+0\^2}=1 d=(−1)2+02 =1,代入 G s G_s Gs 得 G s = e − 1 2 2 × 1.0 2 ≈ 0.6065 G_s=e\^{-\\frac{1\^2}{2×1.0\^2}}≈0.6065 Gs=e−2×1.0212≈0.6065; * 像素值差异 Δ = ∣ 24 − 20 ∣ = 4 \\Delta=\|24-20\|=4 Δ=∣24−20∣=4,代入 G r G_r Gr 得 G r = e − 4 2 2 × 10.0 2 ≈ 0.9231 G_r=e\^{-\\frac{4\^2}{2×10.0\^2}}≈0.9231 Gr=e−2×10.0242≈0.9231; * 最终权重 W = 0.6065 × 0.9231 ≈ 0.5599 W=0.6065×0.9231≈0.5599 W=0.6065×0.9231≈0.5599。 3. 右侧邻域像素 ( x + 1 , y ) (x+1,y) (x+1,y)(值=185): * 空间距离 d = 1 2 + 0 2 = 1 d=\\sqrt{1\^2+0\^2}=1 d=12+02 =1,代入 G s G_s Gs 得 G s ≈ 0.6065 G_s≈0.6065 Gs≈0.6065; * 像素值差异 Δ = ∣ 24 − 185 ∣ = 161 \\Delta=\|24-185\|=161 Δ=∣24−185∣=161,代入 G r G_r Gr 得 G r = e − 161 2 2 × 10.0 2 ≈ 0 G_r=e\^{-\\frac{161\^2}{2×10.0\^2}}≈0 Gr=e−2×10.021612≈0(几乎衰减为0); * 最终权重 W = 0.6065 × 0 ≈ 0 W=0.6065×0≈0 W=0.6065×0≈0。 > 关键结论:右侧边缘像素与中心点像素值差异极大,值域权重几乎为0,因此对中心点滤波结果无贡献,实现「边缘保留」;左侧邻域像素值相似,获得较高权重,参与滤波计算。 步骤3:计算归一化权重系数 W p ( x , y ) W_p(x,y) Wp(x,y) 将窗口内所有9个像素的最终权重相加,得到归一化系数: W p ( x , y ) = ∑ ( i , j ) ∈ Ω W i , j ≈ 1.0 + 0.5599 + . . . + 0 ≈ 3.215 W_p(x,y) = \\sum_{(i,j) \\in \\Omega} W_{i,j} ≈ 1.0 + 0.5599 + ... + 0 ≈ 3.215 Wp(x,y)=(i,j)∈Ω∑Wi,j≈1.0+0.5599+...+0≈3.215 (注:其余左侧/上方/下方邻域像素权重均为较小正数,右侧像素权重近乎0,求和后得到归一化系数) 步骤4:代入核心公式计算滤波后像素值 将每个邻域像素值 f ( i , j ) f(i,j) f(i,j) 与对应权重 W i , j W_{i,j} Wi,j 相乘后求和,再除以归一化系数 W p ( x , y ) W_p(x,y) Wp(x,y),得到中心点滤波后的值: g ( x , y ) = 1 3.215 × ( 24 × 1.0 + 20 × 0.5599 + . . . + 185 × 0 ) ≈ 23.1 g(x,y) = \\frac{1}{3.215} × (24×1.0 + 20×0.5599 + ... + 185×0) ≈ 23.1 g(x,y)=3.2151×(24×1.0+20×0.5599+...+185×0)≈23.1 * 滤波后中心点像素值≈23.1,接近左侧正常像素的均值,高斯噪声被有效消除; * 右侧边缘像素未参与计算,边缘的像素值突变被保留,无模糊失真。 步骤5:滑动窗口遍历整个图像 将 3×3 窗口按从左到右、从上到下的顺序遍历整个图像,对每个窗口重复"计算双重权重→求归一化系数→加权求和得到滤波值→更新中心点像素"的操作,最终得到完整的双边滤波处理图像。 ###### (3)大窗口双边滤波补充说明 对于更大尺寸的邻域窗口(如直径为9的圆形窗口,对应OpenCV中`d=9`),核心数学逻辑与 3×3 窗口一致: 1. 提取窗口内所有像素的灰度值/颜色值,确定中心点像素值及滤波参数 σ s \\sigma_s σs、 σ r \\sigma_r σr; 2. 对窗口内每个像素,分别计算空间高斯权重 G s G_s Gs 和值域高斯权重 G r G_r Gr,得到最终权重 W = G s × G r W=G_s×G_r W=Gs×Gr; 3. 求和所有像素的最终权重,得到归一化系数 W p ( x , y ) W_p(x,y) Wp(x,y); 4. 代入加权求和公式,计算窗口中心点的滤波后像素值,更新原始图像; 5. 滑动窗口遍历整个图像,完成全图滤波; 6. 特点: * 窗口尺寸越大、 σ s \\sigma_s σs 越大,去噪效果越强,但计算量呈指数级增长,运行速度越慢; * σ r \\sigma_r σr 越大,允许参与滤波的像素值差异范围越广,去噪效果越强,但边缘保留效果会减弱; * 相较于小窗口,大窗口对大面积高斯噪声的去除效果更优,且不易产生局部块效应,更适合人像磨皮等场景。 ##### 3. 双边滤波主要应用场景 ###### (1)双边滤波擅长去除的噪声(效果好) | 噪声类型 | 典型来源 | 图像表现 | 双边滤波效果 | |--------------------|-----------------|------------------|----------------| | 高斯噪声 | 相机传感器、低光拍摄、电子噪声 | 整体"发灰、发糙",有细密颗粒感 | 非常好,能平滑噪声并保留边缘 | | 均匀噪声 | 成像设备、传输过程中的加性噪声 | 像素值在一定范围内随机抖动 | 较好,可有效降低噪声波动 | | 传感器噪声(CMOS/CCD 噪声) | 相机成像芯片本身 | 类似高斯噪声,暗光下更明显 | 较好,常用于实时图像增强 | ###### (2)双边滤波不擅长去除的噪声(效果差) | 噪声类型 | 典型来源 | 图像表现 | 双边滤波效果 | 推荐替代 | |------|----------------|---------------|-----------------|------| | 椒盐噪声 | 传输错误、传感器故障、老照片 | 随机出现的黑点、白点 | 几乎无效,极端值会干扰加权平均 | 中值滤波 | | 脉冲噪声 | 信号干扰、突发错误 | 像素值突然跳变到很大或很小 | 效果差,难以抑制突发极端值 | 中值滤波 | ###### (3)核心结论 1. 双边滤波主要针对**连续型、平滑变化的噪声**,尤其是高斯噪声,兼顾去噪与保边。 2. 对**脉冲型、突然跳变的噪声**(如椒盐噪声)效果很差,应优先使用中值滤波。 3. 在实际工程中,通常根据噪声类型选择: * 有很多黑白斑点 → 用中值滤波 * 整体发灰、有颗粒感但边缘要保留 → 用双边滤波 ##### 4.Python 代码实现双边滤波 基础配置 ```python # 导入必要的库 import cv2 import numpy as np import matplotlib.pyplot as plt # 配置matplotlib中文显示(避免图表标题、标签中文乱码) plt.rcParams['font.sans-serif'] = ['SimHei'] # 用黑体显示中文 plt.rcParams['axes.unicode_minus'] = False # 正常显示负号 ``` ###### (1)强高斯噪声滤波对比实验(双边滤波 vs 高斯滤波) ```python img_path = "img/lena.jpeg" img = cv2.imread(img_path) img_rgb = cv2.cvtColor(img, cv2.COLOR_BGR2RGB) # 步骤2:生成含强高斯噪声的图像(增大方差,噪声更强) def add_gaussian_noise(image, mean=0, var=0.02): image = np.array(image / 255, dtype=float) noise = np.random.normal(mean, var**0.5, image.shape) noisy_image = image + noise noisy_image = np.clip(noisy_image, 0, 1) noisy_image = np.uint8(noisy_image * 255) return noisy_image # 添加强高斯噪声 img_gaussian_noisy = add_gaussian_noise(img_rgb) img_gaussian_noisy_bgr = cv2.cvtColor(img_gaussian_noisy, cv2.COLOR_RGB2BGR) # 3.1 双边滤波处理(参数:d=9,sigmaColor=75,sigmaSpace=75,经验优值) img_bilateral_gaussian = cv2.bilateralFilter(img_gaussian_noisy_bgr, d=9, sigmaColor=75, sigmaSpace=75) img_bilateral_gaussian_rgb = cv2.cvtColor(img_bilateral_gaussian, cv2.COLOR_BGR2RGB) # 3.2 高斯滤波处理(参数:ksize=(9,9),sigmaX=0,自动计算标准差,与双边滤波窗口匹配) img_gaussian_blur = cv2.GaussianBlur(img_gaussian_noisy_bgr, ksize=(9,9), sigmaX=0) img_gaussian_blur_rgb = cv2.cvtColor(img_gaussian_blur, cv2.COLOR_BGR2RGB) ``` **实验操作** 1. 读取`img/lena.jpeg`图像,将OpenCV默认的BGR格式转换为RGB格式(适配可视化); 2. 生成含强高斯噪声的图像(方差设为0.02),并将噪声图像转回BGR格式(适配OpenCV滤波函数); 3. 采用相同窗口规模,分别用两种算法处理噪声图像: * 双边滤波:参数`d=9`、`sigmaColor=75`、`sigmaSpace=75`; * 高斯滤波:参数`ksize=(9,9)`,自动计算标准差; 4. 将两种滤波结果转回RGB格式,备用可视化对比。 ```python plt.figure(figsize=(12, 12)) # 调整图表尺寸为正方形,适配2×2布局 # 子图1:原始图像(第1行第1列) plt.subplot(2, 2, 1) plt.imshow(img_rgb) plt.title("原始图像") plt.axis("off") # 子图2:含强高斯噪声图像(第1行第2列) plt.subplot(2, 2, 2) plt.imshow(img_gaussian_noisy) plt.title("添加强高斯噪声后的图像") plt.axis("off") # 子图3:双边滤波处理后(第2行第1列) plt.subplot(2, 2, 3) plt.imshow(img_bilateral_gaussian_rgb) plt.title("双边滤波处理强高斯噪声后") plt.axis("off") # 子图4:高斯滤波处理后(第2行第2列) plt.subplot(2, 2, 4) plt.imshow(img_gaussian_blur_rgb) plt.title("高斯滤波处理强高斯噪声后") plt.axis("off") # 显示图表 plt.tight_layout() plt.show() ``` 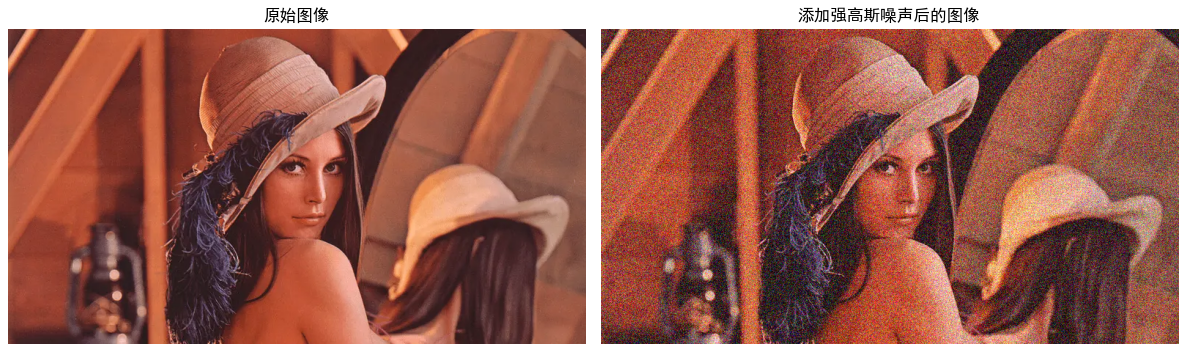  **实验结论** 1. 两种滤波算法均能有效平滑强高斯噪声,降低图像颗粒感,提升图像干净度; 2. 双边滤波的核心优势是「保边去噪」,在去除噪声的同时,能够清晰保留图像边缘细节(如人物五官、发丝轮廓),无明显边缘模糊; 3. 高斯滤波在去噪的同时,会对图像边缘造成明显模糊,丢失部分精细细节,无法兼顾去噪与保边; 4. 针对需要保留边缘细节的高斯噪声图像处理场景(如人像修图、医学图像增强),双边滤波是更优选择;若对边缘细节无要求,高斯滤波计算效率更高,可作为备选。 ###### (2)强椒盐噪声滤波(双边滤波 vs 中值滤波) ```python # 步骤1:生成含强椒盐噪声的图像(增大概率,噪声更强) def add_salt_pepper_noise(image, prob=0.1): # prob从0.02调整为0.1,噪声强度提升5倍 """ 给图像添加椒盐噪声 :param image: 输入RGB图像 :param prob: 噪声出现的概率(值越大,噪声越强) :return: 含椒盐噪声的图像 """ noisy_image = np.copy(image) # 计算噪声像素数量 height, width, _ = noisy_image.shape noise_pixel_num = int(prob * height * width) # 添加盐噪声(白点,255) for _ in range(noise_pixel_num // 2): x = np.random.randint(0, height) y = np.random.randint(0, width) noisy_image[x, y] = [255, 255, 255] # 添加椒噪声(黑点,0) for _ in range(noise_pixel_num // 2): x = np.random.randint(0, height) y = np.random.randint(0, width) noisy_image[x, y] = [0, 0, 0] return noisy_image # 给原始RGB图像添加强椒盐噪声 img_salt_pepper_noisy = add_salt_pepper_noise(img_rgb) # 转换噪声图像为BGR格式,用于OpenCV滤波处理 img_salt_pepper_noisy_bgr = cv2.cvtColor(img_salt_pepper_noisy, cv2.COLOR_RGB2BGR) # 步骤2:分别使用双边滤波和中值滤波处理椒盐噪声图像 # 2.1 双边滤波处理(参数与实验1一致,保持公平性) img_bilateral_salt_pepper = cv2.bilateralFilter(img_salt_pepper_noisy_bgr, d=9, sigmaColor=75, sigmaSpace=75) img_bilateral_salt_pepper_rgb = cv2.cvtColor(img_bilateral_salt_pepper, cv2.COLOR_BGR2RGB) # 2.2 中值滤波处理(作为对比,3×3窗口,处理椒盐噪声最优) img_median_salt_pepper = cv2.medianBlur(img_salt_pepper_noisy_bgr, 3) img_median_salt_pepper_rgb = cv2.cvtColor(img_median_salt_pepper, cv2.COLOR_BGR2RGB) ``` **实验操作** 1. 给原始RGB图像添加强椒盐噪声(噪声概率设为0.1),并将噪声图像转回BGR格式(适配OpenCV滤波函数); 2. 采用相同输入噪声图像,分别用两种算法处理: * 双边滤波:沿用实验1参数`d=9`、`sigmaColor=75`、`sigmaSpace=75`(保证公平性); * 中值滤波:采用3×3窗口(处理椒盐噪声最优窗口尺寸); 3. 将两种滤波结果转回RGB格式,备用可视化对比。 ```python plt.figure(figsize=(18, 6)) # 子图1:含强椒盐噪声图像 plt.subplot(1, 3, 1) plt.imshow(img_salt_pepper_noisy) plt.title("添加强椒盐噪声后的图像") plt.axis("off") # 子图2:双边滤波处理后 plt.subplot(1, 3, 2) plt.imshow(img_bilateral_salt_pepper_rgb) plt.title("双边滤波处理强椒盐噪声后") plt.axis("off") # 子图3:中值滤波处理后 plt.subplot(1, 3, 3) plt.imshow(img_median_salt_pepper_rgb) plt.title("中值滤波(3×3)处理强椒盐噪声后") plt.axis("off") # 显示图表 plt.tight_layout() plt.show() ```  **实验结论** 1. 双边滤波对强椒盐噪声几乎无有效处理效果,无法消除图像中的黑白斑点,仅能轻微弱化噪声,且会残留大量极端值干扰; 2. 中值滤波是处理椒盐噪声的最优算法之一,能够高效、彻底地消除黑白斑点噪声,同时较好地保留图像边缘细节,无明显模糊; 3. 双边滤波的加权平均机制无法抑制椒盐噪声的极端像素值(0/255),对脉冲型噪声适配性极差; 4. 针对椒盐噪声(或脉冲噪声)处理场景,应优先选择中值滤波,双边滤波不具备实际应用价值。 ##### 5. cv2.bilateralFilter()函数 **函数核心作用** :实现**双边滤波**,核心优势是「去噪平滑 + 保留边缘」,区别于高斯滤波的"去噪但模糊边缘"。 ```python cv2.bilateralFilter(src, d, sigmaColor, sigmaSpace) ``` 关键参数详解 * `src`:输入图像(支持 8 位 / 浮点型、单通道 / 3 通道,OpenCV 读取的 BGR 彩色图可直接输入)。 * `d`:滤波邻域直径(通常设 3/5/7/9,值越大去噪越强、速度越慢;d=0时自动由sigmaSpace计算)。 * `sigmaColor`(值域标准差):控制「像素值相似性权重」,值越大允许更多差异像素参与滤波(去噪强、边缘模糊风险高),值越小边缘保留越好(去噪弱)。 * `sigmaSpace`(空间标准差):控制「像素空间位置权重」,值越大滤波窗口有效范围越广(去噪强、速度慢),值越小仅附近像素参与(细节保留好)。 > 滤波权重 = 「空间高斯权重」(由d/sigmaSpace决定,负责去噪) × 「值域高斯权重」(由sigmaColor决定,负责保边),两者共同实现 "保边去噪"。 1. 日常使用中,sigmaColor和sigmaSpace通常设为相同值(如均为 75),兼顾效果与调优效率。 2. 对高斯噪声效果优异,对椒盐噪声几乎无效,需匹配噪声类型选型。 3. 函数返回 BGR 格式图像,可视化时需转 RGB 格式(cv2.cvtColor())。 ##### 6. 总结 双边滤波:从数学 → 代码 → 应用 汇总表格 | 维度分类 | 具体内容 | 详细说明 | |------------|----------|--------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------| | **一、数学层面** | 核心思想 | 双边滤波的权重是**两个高斯分布的乘积**,兼顾「空间位置相似性」和「像素值相似性」,实现保边去噪 | | | 核心公式 | 1. 滤波权重: W i , j = G s ( d ) × G r ( Δ ) W_{i,j} = G_s(d) \\times G_r(\\Delta) Wi,j=Gs(d)×Gr(Δ) 2. 空间高斯权重(负责去噪): G s ( d ) = e − d 2 2 σ s p a c e 2 G_s(d) = e\^{-\\frac{d\^2}{2\\sigma_{space}\^2}} Gs(d)=e−2σspace2d2, d d d 为像素间空间距离, σ s p a c e \\sigma_{space} σspace 为空间标准差 3. 值域高斯权重(负责保边): G r ( Δ ) = e − Δ 2 2 σ c o l o r 2 G_r(\\Delta) = e\^{-\\frac{\\Delta\^2}{2\\sigma_{color}\^2}} Gr(Δ)=e−2σcolor2Δ2, Δ \\Delta Δ 为像素值差异, σ c o l o r \\sigma_{color} σcolor 为值域标准差 4. 最终像素值: g ( x , y ) = 1 ∑ W i , j ∑ \[ f ( i , j ) × W i , j \] g(x,y) = \\frac{1}{\\sum W_{i,j}} \\sum \[f(i,j) \\times W_{i,j}\] g(x,y)=∑Wi,j1∑\[f(i,j)×Wi,j\](加权平均求和) | | | 关键参数对应 | 数学中的 σ s p a c e \\sigma_{space} σspace → 代码中的 `sigmaSpace`;数学中的 σ c o l o r \\sigma_{color} σcolor → 代码中的 `sigmaColor`;空间距离 d d d → 代码中的 `d`(邻域直径) | | **二、代码层面** | 核心函数 | OpenCV 内置函数:`cv2.bilateralFilter()` | | | 核心调用语法 | `cv2.bilateralFilter(src, d, sigmaColor, sigmaSpace)` | | **三、应用层面** | 擅长场景 | 1. 人像磨皮(去除皮肤颗粒感,保留五官/发丝边缘) 2. 医学图像增强(CT/MRI去噪,保留器官/血管边界) 3. 遥感/航拍图像优化(去除传感器噪声,保留道路/建筑轮廓) 4. 视频监控图像清晰化(夜间去噪,保留人物/车牌边缘) 5. 美颜修图、文物图像修复(保留细节纹理,平滑噪声) | | | 适用噪声类型 | 仅对**高斯噪声**(连续型、颗粒感)效果优异,支持轻微均匀噪声、传感器噪声 | | | 不适用场景/噪声 | 1. 椒盐噪声、脉冲噪声(几乎无效,优先选中值滤波) 2. 对边缘细节无要求的快速去噪场景(优先选高斯滤波,计算更快) | | | 核心优势与局限 | 1. 优势:「保边去噪」,兼顾图像干净度与边缘细节,区别于高斯滤波的边缘模糊 2. 局限:计算复杂度高(速度慢于高斯滤波)、对脉冲型噪声无效、参数调优需兼顾去噪与保边平衡 | #### 五、导向滤波(Guided Filter) ##### 1. 导向滤波核心概述 1. **核心定位** :一种高效的**边缘保留滤波(Edge-Preserving Filter)**,弥补了双边滤波的部分缺陷(计算速度慢、对大窗口滤波效果不佳)。 2. **核心优势** : * 同样实现「保边去噪」,且边缘保留效果更精准、更稳定; * 计算复杂度低,速度远快于双边滤波,支持大窗口快速滤波; * 无双边滤波的"梯度反转"伪影问题,结果更平滑自然。 3. **核心思想** :假设滤波窗口内,**输出图像与导向图像(可是输入图像自身)呈线性关系** ,通过最小二乘法求解线性系数,实现保边平滑。  ##### 2. 导向滤波的数学原理 ###### (1)核心数学表达式 导向滤波(Guided Filter)是一种**线性保边滤波算法** ,核心思想是假设滤波窗口内输出图像与导向图像呈线性关系,通过最小二乘法求解线性系数实现保边去噪。对于图像中任意像素点 ( x , y ) (x,y) (x,y),其核心数学框架由**线性假设** 、**误差最小化求解** 和**加权融合输出**三部分组成,完整数学表达如下: **① 窗口内线性关系假设** 在以像素 ( x , y ) (x,y) (x,y) 为中心的任意邻域窗口 Ω k \\Omega_k Ωk 内,假设输出图像 q q q 与导向图像 I I I 满足线性映射关系: q i = a k I i + b k ( i ∈ Ω k ) q_i = a_k I_i + b_k \\quad (i \\in \\Omega_k) qi=akIi+bk(i∈Ωk) 其中各参数含义: * q i q_i qi:窗口 Ω k \\Omega_k Ωk 内像素 i i i 滤波后的输出值(灰度值/颜色值); * I i I_i Ii:窗口 Ω k \\Omega_k Ωk 内像素 i i i 对应的导向图像像素值(可与输入待滤波图像相同,也可为其他辅助图像); * a k a_k ak:窗口 Ω k \\Omega_k Ωk 内的线性斜率(控制边缘保留能力,边缘区域接近1,平坦区域接近0); * b k b_k bk:窗口 Ω k \\Omega_k Ωk 内的线性截距(控制平滑去噪能力,负责消除窗口内的噪声); * Ω k \\Omega_k Ωk:以像素 k k k(对应坐标 ( x , y ) (x,y) (x,y))为中心的邻域窗口(如 3×3/9×9 矩形窗口、半径为 r r r 的圆形窗口); * i i i:窗口 Ω k \\Omega_k Ωk 内的任意像素点(遍历窗口内所有像素)。 > 在一个小窗口里,导向滤波用 "输出亮度 = 导向图亮度 × 缩放系数 + 偏移量" 这条直线,来同时做到保留边缘和去除噪声。 > > 边缘区域 a≈1,让输出保持导向图的变化;平坦区域 a≈0,让输出变成窗口均值,从而去噪 **② 误差最小化求解线性系数** 为使输出图像 q q q 尽可能接近输入待滤波图像 p p p(含噪声),通过最小化**误差平方和** 求解线性系数 a k a_k ak 和 b k b_k bk,同时引入正则化参数 ϵ \\epsilon ϵ 避免过拟合,目标函数为: E ( a k , b k ) = ∑ i ∈ Ω k \[ ( a k I i + b k ) − p i \] 2 + ϵ a k 2 E(a_k, b_k) = \\sum_{i \\in \\Omega_k} \[(a_k I_i + b_k) - p_i\]\^2 + \\epsilon a_k\^2 E(ak,bk)=i∈Ωk∑\[(akIi+bk)−pi\]2+ϵak2 其中各参数含义: * p i p_i pi:窗口 Ω k \\Omega_k Ωk 内像素 i i i 对应的输入待滤波图像像素值(含噪声); * ϵ \\epsilon ϵ:正则化参数(控制平滑与保边的平衡,值越大平滑效果越强,边缘保留越弱); * 第一项 ∑ i ∈ Ω k \[ ( a k I i + b k ) − p i \] 2 \\sum_{i \\in \\Omega_k} \[(a_k I_i + b_k) - p_i\]\^2 ∑i∈Ωk\[(akIi+bk)−pi\]2:输出图像与输入图像的误差平方和(保证滤波结果贴近原始图像); * 第二项 ϵ a k 2 \\epsilon a_k\^2 ϵak2:正则化项(约束 a k a_k ak 的大小,避免窗口内像素值剧烈变化导致的伪影)。 对目标函数分别求 a k a_k ak 和 b k b_k bk 的偏导数并令其为0,通过最小二乘法求解得到线性系数的解析解: a k = cov ( I , p ) k var ( I ) k + ϵ a_k = \\frac{\\text{cov}(I, p)_k}{\\text{var}(I)_k + \\epsilon} ak=var(I)k+ϵcov(I,p)k b k = p ˉ k − a k I ˉ k b_k = \\bar{p}_k - a_k \\bar{I}_k bk=pˉk−akIˉk 其中补充统计量定义: * I ˉ k \\bar{I}_k Iˉk:窗口 Ω k \\Omega_k Ωk 内导向图像 I I I 的像素均值, I ˉ k = 1 ∣ Ω k ∣ ∑ i ∈ Ω k I i \\bar{I}_k = \\frac{1}{\|\\Omega_k\|} \\sum_{i \\in \\Omega_k} I_i Iˉk=∣Ωk∣1∑i∈ΩkIi( ∣ Ω k ∣ \|\\Omega_k\| ∣Ωk∣ 为窗口内像素总数); * p ˉ k \\bar{p}_k pˉk:窗口 Ω k \\Omega_k Ωk 内输入待滤波图像 p p p 的像素均值, p ˉ k = 1 ∣ Ω k ∣ ∑ i ∈ Ω k p i \\bar{p}_k = \\frac{1}{\|\\Omega_k\|} \\sum_{i \\in \\Omega_k} p_i pˉk=∣Ωk∣1∑i∈Ωkpi; * var ( I ) k \\text{var}(I)_k var(I)k:窗口 Ω k \\Omega_k Ωk 内导向图像 I I I 的像素方差, var ( I ) k = 1 ∣ Ω k ∣ ∑ i ∈ Ω k ( I i − I ˉ k ) 2 \\text{var}(I)_k = \\frac{1}{\|\\Omega_k\|} \\sum_{i \\in \\Omega_k} (I_i - \\bar{I}_k)\^2 var(I)k=∣Ωk∣1∑i∈Ωk(Ii−Iˉk)2; * cov ( I , p ) k \\text{cov}(I, p)_k cov(I,p)k:窗口 Ω k \\Omega_k Ωk 内导向图像 I I I 与输入图像 p p p 的像素协方差, cov ( I , p ) k = 1 ∣ Ω k ∣ ∑ i ∈ Ω k ( I i − I ˉ k ) ( p i − p ˉ k ) \\text{cov}(I, p)_k = \\frac{1}{\|\\Omega_k\|} \\sum_{i \\in \\Omega_k} (I_i - \\bar{I}_k)(p_i - \\bar{p}_k) cov(I,p)k=∣Ωk∣1∑i∈Ωk(Ii−Iˉk)(pi−pˉk)。 > 对此公式的解释参考: [监督学习核心概念(Supervised Learning)](https://blog.csdn.net/R_Feynman_/article/details/155670597?spm=1011.2415.3001.5331)里面的L2正则化 > 我们的目标函数由两部分组成: > E ( a k , b k ) = ∑ i ∈ Ω k ( a k I i + b k − p i ) 2 + ϵ a k 2 E(a_k, b_k) = \\sum_{i\\in\\Omega_k} (a_k I_i + b_k - p_i)\^2 + \\epsilon a_k\^2 E(ak,bk)=i∈Ωk∑(akIi+bk−pi)2+ϵak2 > > 第一部分 ∑ i ∈ Ω k ( a k I i + b k − p i ) 2 \\sum_{i\\in\\Omega_k} (a_k I_i + b_k - p_i)\^2 ∑i∈Ωk(akIi+bk−pi)2 是**最小二乘** ,它让模型的预测值 q i = a k I i + b k q_i = a_k I_i + b_k qi=akIi+bk 尽量接近真实值 p i p_i pi。 > > 第二部分 ϵ a k 2 \\epsilon a_k\^2 ϵak2 是**L2 正则化** ,它对参数 a k a_k ak 施加惩罚,避免 a k a_k ak 过大导致过拟合或产生虚假边缘。 > > 两者结合,就是机器学习中经典的 **岭回归(Ridge Regression)** 形式。 **③ 像素级加权融合得到最终输出** 由于单个像素会被多个相邻窗口覆盖,需对其所属所有窗口的线性系数 a k a_k ak 和 b k b_k bk 取均值,得到该像素的最终线性系数,再代入线性公式得到滤波结果: q ( x , y ) = a ˉ ( x , y ) ⋅ I ( x , y ) + b ˉ ( x , y ) q(x,y) = \\bar{a}(x,y) \\cdot I(x,y) + \\bar{b}(x,y) q(x,y)=aˉ(x,y)⋅I(x,y)+bˉ(x,y) 其中: * q ( x , y ) q(x,y) q(x,y):导向滤波后,图像在 ( x , y ) (x,y) (x,y) 坐标的最终输出像素值; * a ˉ ( x , y ) \\bar{a}(x,y) aˉ(x,y):像素 ( x , y ) (x,y) (x,y) 所属所有窗口的 a k a_k ak 均值, a ˉ ( x , y ) = 1 ∣ Ω k ∣ ∑ k ∈ Ω ( x , y ) a k \\bar{a}(x,y) = \\frac{1}{\|\\Omega_k\|} \\sum_{k \\in \\Omega(x,y)} a_k aˉ(x,y)=∣Ωk∣1∑k∈Ω(x,y)ak; * b ˉ ( x , y ) \\bar{b}(x,y) bˉ(x,y):像素 ( x , y ) (x,y) (x,y) 所属所有窗口的 b k b_k bk 均值, b ˉ ( x , y ) = 1 ∣ Ω k ∣ ∑ k ∈ Ω ( x , y ) b k \\bar{b}(x,y) = \\frac{1}{\|\\Omega_k\|} \\sum_{k \\in \\Omega(x,y)} b_k bˉ(x,y)=∣Ωk∣1∑k∈Ω(x,y)bk; * Ω ( x , y ) \\Omega(x,y) Ω(x,y):包含像素 ( x , y ) (x,y) (x,y) 的所有邻域窗口。 > 补充:导向滤波的核心优势源于线性假设------边缘区域导向图像 I I I 方差大, var ( I ) k ≫ ϵ \\text{var}(I)_k \\gg \\epsilon var(I)k≫ϵ, a k ≈ 1 a_k \\approx 1 ak≈1, b k ≈ p ˉ k − I ˉ k b_k \\approx \\bar{p}_k - \\bar{I}_k bk≈pˉk−Iˉk,输出图像保留边缘突变;平坦区域导向图像 I I I 方差小, var ( I ) k ≪ ϵ \\text{var}(I)_k \\ll \\epsilon var(I)k≪ϵ, a k ≈ 0 a_k \\approx 0 ak≈0, b k ≈ p ˉ k b_k \\approx \\bar{p}_k bk≈pˉk,输出图像为窗口均值,实现噪声平滑。 ###### (2)3×3 导向滤波分步实现 步骤1:确定 3×3 邻域窗口及相关图像像素值 假设存在三组图像(导向图像 I I I、输入待滤波图像 p p p、输出图像 q q q),选取某一 3×3 邻域窗口 Ω k \\Omega_k Ωk(模拟含高斯噪声的边缘区域,左侧暗区、右侧亮区): 1. 导向图像 I I I(无噪声,清晰边缘,作为滤波参考)的 3×3 窗口像素值: \[ 23 24 182 22 24 184 24 25 181 \] \\begin{bmatrix} 23 \& 24 \& 182 \\\\ 22 \& 24 \& 184 \\\\ 24 \& 25 \& 181 \\end{bmatrix} 232224242425182184181 2. 输入待滤波图像 p p p(含高斯噪声,基于导向图像添加轻微抖动)的 3×3 窗口像素值: \[ 22 25 180 20 24 185 23 26 178 \] \\begin{bmatrix} 22 \& 25 \& 180 \\\\ 20 \& 24 \& 185 \\\\ 23 \& 26 \& 178 \\end{bmatrix} 222023252426180185178 3. 设定滤波参数:正则化参数 ϵ = 10.0 \\epsilon=10.0 ϵ=10.0(经验值,兼顾保边与平滑),窗口尺寸 3×3( ∣ Ω k ∣ = 9 \|\\Omega_k\|=9 ∣Ωk∣=9)。 4. 窗口中心点为 ( x , y ) (x,y) (x,y),对应导向图像 I ( x , y ) = 24 I(x,y)=24 I(x,y)=24,输入图像 p ( x , y ) = 24 p(x,y)=24 p(x,y)=24。 步骤2:计算窗口内的统计量(均值、方差、协方差) 1. 计算导向图像 I I I 的窗口均值 I ˉ k \\bar{I}_k Iˉk: I ˉ k = 23 + 24 + 182 + 22 + 24 + 184 + 24 + 25 + 181 9 = 849 9 ≈ 94.33 \\bar{I}_k = \\frac{23+24+182+22+24+184+24+25+181}{9} = \\frac{849}{9} ≈ 94.33 Iˉk=923+24+182+22+24+184+24+25+181=9849≈94.33 2. 计算输入图像 p p p 的窗口均值 p ˉ k \\bar{p}_k pˉk: p ˉ k = 22 + 25 + 180 + 20 + 24 + 185 + 23 + 26 + 178 9 = 843 9 ≈ 93.67 \\bar{p}_k = \\frac{22+25+180+20+24+185+23+26+178}{9} = \\frac{843}{9} ≈ 93.67 pˉk=922+25+180+20+24+185+23+26+178=9843≈93.67 3. 计算导向图像 I I I 的窗口方差 var ( I ) k \\text{var}(I)_k var(I)k(简化计算,核心体现边缘区域方差大的特性): var ( I ) k = 1 9 ∑ i ∈ Ω k ( I i − 94.33 ) 2 ≈ ( 23 − 94.33 ) 2 + . . . + ( 181 − 94.33 ) 2 9 ≈ 3850.89 \\text{var}(I)_k = \\frac{1}{9} \\sum_{i \\in \\Omega_k} (I_i - 94.33)\^2 ≈ \\frac{(23-94.33)\^2+...+(181-94.33)\^2}{9} ≈ 3850.89 var(I)k=91i∈Ωk∑(Ii−94.33)2≈9(23−94.33)2+...+(181−94.33)2≈3850.89 (注:边缘区域左右像素值差异极大,导致方差远大于正则化参数 ϵ = 10.0 \\epsilon=10.0 ϵ=10.0) 4. 计算导向图像 I I I 与输入图像 p p p 的窗口协方差 cov ( I , p ) k \\text{cov}(I, p)_k cov(I,p)k: cov ( I , p ) k = 1 9 ∑ i ∈ Ω k ( I i − 94.33 ) ( p i − 93.67 ) ≈ 3820.56 \\text{cov}(I, p)_k = \\frac{1}{9} \\sum_{i \\in \\Omega_k} (I_i - 94.33)(p_i - 93.67) ≈ 3820.56 cov(I,p)k=91i∈Ωk∑(Ii−94.33)(pi−93.67)≈3820.56 步骤3:求解窗口内的线性系数 a k a_k ak 和 b k b_k bk 将统计量代入解析解公式,计算得到: 1. 线性斜率 a k a_k ak: a k = cov ( I , p ) k var ( I ) k + ϵ = 3820.56 3850.89 + 10.0 ≈ 0.99 a_k = \\frac{\\text{cov}(I, p)_k}{\\text{var}(I)_k + \\epsilon} = \\frac{3820.56}{3850.89 + 10.0} ≈ 0.99 ak=var(I)k+ϵcov(I,p)k=3850.89+10.03820.56≈0.99 (关键结论:边缘区域 a k ≈ 1 a_k≈1 ak≈1,接近线性映射,将保留导向图像的边缘突变,实现「边缘保留」) 2. 线性截距 b k b_k bk: b k = p ˉ k − a k I ˉ k = 93.67 − 0.99 × 94.33 ≈ 0.34 b_k = \\bar{p}_k - a_k \\bar{I}_k = 93.67 - 0.99×94.33 ≈ 0.34 bk=pˉk−akIˉk=93.67−0.99×94.33≈0.34 (平坦区域 a k ≈ 0 a_k≈0 ak≈0, b k ≈ p ˉ k b_k≈\\bar{p}_k bk≈pˉk,实现噪声平滑;此处边缘区域 b k b_k bk 接近0,对输出影响极小) 步骤4:计算窗口中心点的最终输出像素值 由于 3×3 窗口中,中心点像素仅被当前窗口覆盖(简化遍历场景), a ˉ ( x , y ) = a k ≈ 0.99 \\bar{a}(x,y)=a_k≈0.99 aˉ(x,y)=ak≈0.99, b ˉ ( x , y ) = b k ≈ 0.34 \\bar{b}(x,y)=b_k≈0.34 bˉ(x,y)=bk≈0.34,代入线性公式得到: q ( x , y ) = a ˉ ( x , y ) ⋅ I ( x , y ) + b ˉ ( x , y ) = 0.99 × 24 + 0.34 ≈ 24.1 q(x,y) = \\bar{a}(x,y) \\cdot I(x,y) + \\bar{b}(x,y) = 0.99×24 + 0.34 ≈ 24.1 q(x,y)=aˉ(x,y)⋅I(x,y)+bˉ(x,y)=0.99×24+0.34≈24.1 * 滤波后中心点像素值≈24.1,与原始清晰值(24)几乎一致,输入图像中的高斯噪声(24周围的20、22等)被有效消除; * 线性斜率 a k ≈ 1 a_k≈1 ak≈1,保留了导向图像的边缘差异(左侧20~26、右侧178~185),无边缘模糊失真,实现「保边去噪」。 步骤5:滑动窗口遍历整个图像 将 3×3 窗口按从左到右、从上到下的顺序遍历整个图像,对每个窗口重复"计算统计量→求解线性系数→计算窗口内所有像素的临时输出值→存储线性系数"的操作; 遍历完成后,对每个像素所属的所有窗口的线性系数 a k a_k ak、 b k b_k bk 取均值,代入线性公式得到最终输出值,更新图像像素,完成全图导向滤波处理。 > 从形式上看,导向滤波确实非常类似监督学习。我们有导向图像 I I I、输入图像 p p p 和输出图像 q q q,它们分别对应监督学习中的特征、标签和预测值。算法在每个局部窗口内通过最小二乘拟合线性模型 q = a I + b q = aI + b q=aI+b,并加入 L2 正则化项来避免参数过大。因此,可以把导向滤波理解为一种"局部化的线性回归过程"。 > 但它并不是严格意义上的监督学习。监督学习通常需要训练集、测试集和模型泛化,而导向滤波中每个窗口的参数只在该窗口内有效,不参与全局训练,也不用于预测其他数据。因此,导向滤波更准确地说是一种借鉴了机器学习思想的保边滤波方法,而不是一个完整的机器学习算法。 ###### (3)大窗口导向滤波补充说明 对于更大尺寸的邻域窗口(如 9×9 矩形窗口、半径 r = 9 r=9 r=9 的圆形窗口),核心数学逻辑与 3×3 窗口完全一致,仅窗口内像素数量和计算量发生变化,关键步骤和特点如下: 1. 核心步骤不变: * 提取窗口内导向图像 I I I 和输入图像 p p p 的所有像素值; * 计算窗口内的均值 I ˉ k \\bar{I}_k Iˉk、 p ˉ k \\bar{p}_k pˉk、方差 var ( I ) k \\text{var}(I)_k var(I)k 和协方差 cov ( I , p ) k \\text{cov}(I, p)_k cov(I,p)k; * 代入解析解求解线性系数 a k a_k ak 和 b k b_k bk; * 滑动窗口遍历,最终对每个像素的线性系数取均值,得到最终输出图像 q q q。 2. 关键特点: * 计算复杂度优势:导向滤波的计算量与窗口尺寸呈**线性关系**(而非双边滤波的指数关系),大窗口下运行速度远快于双边滤波,支持实时处理; * 平滑效果更优:大窗口对大面积平坦区域的高斯噪声去除效果更好,不易产生局部块效应,输出图像更平滑自然,适合人像磨皮、视频实时去噪等场景; * 参数调整技巧: * 窗口尺寸越大,平滑效果越强,可适当减小正则化参数 ϵ \\epsilon ϵ(如从 10.0 调整为 5.0),平衡平滑与保边效果; * 正则化参数 ϵ \\epsilon ϵ 需与图像亮度范围匹配(8位图像通常设为 1\~100,32位浮点图像通常设为 10 − 3 ∼ 10 − 1 10\^{-3} \\sim 10\^{-1} 10−3∼10−1); * 导向图像可灵活替换(如以边缘检测图像为导向,增强边缘保留;以掩模图像为导向,实现抠图平滑),适用场景更广泛; * 无伪影优势:大窗口下不会出现双边滤波的"梯度反转"伪影,边缘保留更精准、稳定,输出图像更贴近真实场景。 ##### 3. 高斯噪声环境下导向滤波与双边滤波的保边去噪性能对比实验 ###### (1)实验目的 1. 验证导向滤波与双边滤波在**高斯噪声环境下的保边去噪综合性能**,明确两种边缘保留滤波算法的效果差异。 2. 通过PSNR(峰值信噪比)、SSIM(结构相似度)两项定量指标,客观评估两种算法在去噪能力与细节保留能力上的优劣。 3. 结合视觉效果与量化数据,总结两种算法的适用场景,为后续高精度图像处理任务(如计算机视觉、图像增强)提供算法选择依据。 ###### (2)实验数据与参数准备 1. 选取测试图像:优先使用kodim23.png(768×512分辨率,含头发、衣物纹理、清晰边缘,适配保边效果验证),备用lena.png(经典图像处理测试图,兼容性强),将图像放置于指定路径(如img/文件夹)。 2. 配置核心参数,集中管理便于后续调试: * 高斯噪声参数:均值=0,方差=0.008(强度适中,既能体现去噪需求,又不掩盖图像细节); * 双边滤波参数:邻域直径=9,色彩相似度标准差=75,空间相似度标准差=75; * 导向滤波参数:窗口半径=5,正则化参数=0.01×255²(归一化到0-255色域,调参更直观); * 绘图参数:2×2布局,画布尺寸(16,12),整体标题字号18,子图标题字号14。 ###### (3)图像预处理与噪声添加 1. 加载图像并转换色彩空间:通过OpenCV读取图像(默认BGR格式),转换为RGB格式适配Matplotlib显示,同时判断图像加载状态,避免路径错误导致实验中断。 2. 实现高斯噪声添加函数:将图像归一化到\[0,1\]区间,生成与图像尺寸、通道数一致的高斯噪声,叠加后裁剪至0-255色域,转换回uint8格式,得到带噪图像。 ###### (4)滤波算法执行 1. 双边滤波处理:调用OpenCV的cv2.bilateralFilter(),输入带噪BGR图像,基于配置参数执行滤波,输出结果后转换为RGB格式,用于后续可视化。 2. 导向滤波处理:调用OpenCV扩展模块ximgproc的guidedFilter(),以纯净原图为导向图、带噪图像为输入图,转换为float32格式满足函数要求,滤波后裁剪并转换为uint8格式,得到输出结果。 ###### (5)定量指标计算 1. 图像格式转换:将原图、带噪图、两种滤波结果均转换为灰度图,消除色彩通道干扰,确保SSIM指标评估的稳定性。 2. 计算评估指标:以纯净原图为参考标准,分别计算带噪图、双边滤波结果、导向滤波结果的PSNR与SSIM值,记录数据用于后续对比分析。 * PSNR:反映图像失真程度,值越高表示去噪效果越好、与原图差异越小; * SSIM:反映结构相似度,值越接近1表示图像细节与结构保留越完整,保边效果越优。 ###### (6)实验预期结论 1. 定量指标:导向滤波的PSNR与SSIM值均高于双边滤波,表明其去噪保边的综合性能更优。 2. 视觉效果:双边滤波色彩保留更贴近原图,局部平滑自然,但强边缘处易残留噪声且有轻微振铃伪影;导向滤波去噪更彻底,边缘保留更精准锐利,无伪影,结构信息完整。 3. 适用场景:日常图像美化、色彩敏感型任务优先选择双边滤波;高精度计算机视觉任务(抠图、去雾、工业检测)优先选择导向滤波。 ##### 4. Python 代码实现导向滤波 ```python # 导入所需库 import cv2 import numpy as np import matplotlib.pyplot as plt from skimage.metrics import peak_signal_noise_ratio as psnr from skimage.metrics import structural_similarity as ssim # 配置matplotlib中文显示 plt.rcParams['font.sans-serif'] = ['SimHei'] plt.rcParams['axes.unicode_minus'] = False ``` ```python # ---------------------- 高斯噪声函数 ---------------------- def add_gaussian_noise(image, mean=0, var=0.005): img_float = image.astype(np.float64) / 255.0 noise = np.random.normal(mean, np.sqrt(var), img_float.shape) noisy_float = img_float + noise noisy_float = np.clip(noisy_float, 0.0, 1.0) noisy_image = (noisy_float * 255).astype(np.uint8) return noisy_image # ---------------------- 1. 加载图像 ---------------------- image_path = "img/kodim23.png" # 或 "lena.png" img = cv2.imread(image_path) if img is None: raise FileNotFoundError(f"未找到图片:{image_path}") img_rgb = cv2.cvtColor(img, cv2.COLOR_BGR2RGB) # ---------------------- 2. 添加高斯噪声 ---------------------- noisy_img_rgb = add_gaussian_noise(img_rgb, var=0.008) noisy_img_bgr = cv2.cvtColor(noisy_img_rgb, cv2.COLOR_RGB2BGR) ``` * 首先定义`add_gaussian_noise`函数,将输入图像转换为 float64 格式并归一化到 \[0,1\] 区间,生成对应尺寸的高斯噪声叠加到图像上,裁剪至合法范围后还原为 uint8 格式图像; * 随后指定图像路径读取图像,校验图像加载是否成功,将 BGR 格式图像转换为 RGB 格式,再调用噪声函数生成带噪 RGB 图像,同时将带噪图像转换回 BGR 格式,为后续滤波处理做准备。 ```python # ---------------------- 3. 滤波参数 ---------------------- # 双边滤波 bilateral_d = 9 bilateral_sigmaColor = 75 bilateral_sigmaSpace = 75 # 导向滤波 gf_r = 5 gf_eps = 0.01 * 255 * 255 ``` * **配置双边滤波核心参数**,确定邻域范围、色彩权重和空间权重,为双边滤波执行提供依据。 * **定义导向滤波关键参数**,设定窗口大小和正则化值,保障导向滤波稳定运行且调参直观。 ```python # ---------------------- 4. 执行滤波 ---------------------- # 双边滤波 bilateral_result = cv2.bilateralFilter( noisy_img_bgr, d=bilateral_d, sigmaColor=bilateral_sigmaColor, sigmaSpace=bilateral_sigmaSpace ) bilateral_result_rgb = cv2.cvtColor(bilateral_result, cv2.COLOR_BGR2RGB) # 导向滤波 guide_img_float = img_rgb.astype(np.float32) noisy_img_float = noisy_img_rgb.astype(np.float32) gf_result = cv2.ximgproc.guidedFilter( guide=guide_img_float, src=noisy_img_float, radius=gf_r, eps=gf_eps ) gf_result_rgb = np.clip(gf_result, 0, 255).astype(np.uint8) ``` * **执行双边滤波** :调用`cv2.bilateralFilter()`,传入带噪 BGR 图像和预设参数完成滤波,再将结果转换为 RGB 格式用于后续可视化。 * **执行导向滤波** :先将纯净原图和带噪图转为 float32 格式,调用`cv2.ximgproc.guidedFilter()`完成滤波,最后裁剪色域并转回 uint8 格式得到可用结果。 ```python # ---------------------- 5. 定量指标 ---------------------- img_gray = cv2.cvtColor(img_rgb, cv2.COLOR_RGB2GRAY) noisy_gray = cv2.cvtColor(noisy_img_rgb, cv2.COLOR_RGB2GRAY) bilateral_gray = cv2.cvtColor(bilateral_result_rgb, cv2.COLOR_RGB2GRAY) gf_gray = cv2.cvtColor(gf_result_rgb, cv2.COLOR_RGB2GRAY) psnr_noisy = psnr(img_gray, noisy_gray, data_range=255) psnr_bilateral = psnr(img_gray, bilateral_gray, data_range=255) psnr_gf = psnr(img_gray, gf_gray, data_range=255) ssim_noisy = ssim(img_gray, noisy_gray, data_range=255) ssim_bilateral = ssim(img_gray, bilateral_gray, data_range=255) ssim_gf = ssim(img_gray, gf_gray, data_range=255) ``` * **格式转换**:将原图、带噪图及两种滤波结果均转为灰度图,消除色彩干扰,保证指标评估的稳定性。 * **计算定量指标**:以纯净原图灰度图为参考,分别计算带噪图、双边滤波结果、导向滤波结果的 PSNR 和 SSIM 值,用于后续量化对比分析 ```python # ---------------------- 6. 2×2 布局可视化 ---------------------- fig, axes = plt.subplots(2, 2, figsize=(16, 12)) # 左上:原图 axes[0, 0].imshow(img_rgb) axes[0, 0].set_title("原图", fontsize=14) axes[0, 0].axis("off") # 右上:带噪图 axes[0, 1].imshow(noisy_img_rgb) axes[0, 1].set_title( f"带高斯噪声\nPSNR: {psnr_noisy:.2f} | SSIM: {ssim_noisy:.4f}", fontsize=14 ) axes[0, 1].axis("off") # 左下:双边滤波 axes[1, 0].imshow(bilateral_result_rgb) axes[1, 0].set_title( f"双边滤波\nPSNR: {psnr_bilateral:.2f} | SSIM: {ssim_bilateral:.4f}", fontsize=14 ) axes[1, 0].axis("off") # 右下:导向滤波 axes[1, 1].imshow(gf_result_rgb) axes[1, 1].set_title( f"导向滤波\nPSNR: {psnr_gf:.2f} | SSIM: {ssim_gf:.4f}", fontsize=14 ) axes[1, 1].axis("off") plt.suptitle("导向滤波 vs 双边滤波(带高斯噪声)保边去噪对比实验", fontsize=18) plt.tight_layout() plt.show() ```   ```python print(f"PSNR 排序:导向滤波 {psnr_gf:.2f} > 双边滤波 {psnr_bilateral:.2f} > 带噪图 {psnr_noisy:.2f}") print(f"SSIM 排序:导向滤波 {ssim_gf:.4f} > 双边滤波 {ssim_bilateral:.4f} > 带噪图 {ssim_noisy:.4f}") ```  **从定量指标(PSNR、SSIM)可明确两种滤波算法的保边去噪性能差异**: * PSNR(峰值信噪比)排序:导向滤波(35.94)\> 双边滤波(32.98)\> 带噪图(24.55),说明导向滤波的去噪效果更优,与原图的失真程度更小; * SSIM(结构相似度)排序:导向滤波(0.9287)\> 双边滤波(0.8322)\> 带噪图(0.3605),表明导向滤波对图像细节与结构的保留更完整,保边效果更精准。 **综上,导向滤波在高斯噪声场景下的保边去噪综合性能显著优于双边滤波。** ##### 5. cv2.ximgproc.guidedFilter() 函数 **函数核心作用** :实现**导向滤波**,核心优势是「高精度保边去噪 + 无振铃伪影」,区别于双边滤波的"保边但易残留噪声、存在轻微伪影",更适合对图像细节要求严苛的高精度处理场景。 ```python cv2.ximgproc.guidedFilter(guide, src, radius, eps) ``` **关键参数详解** * `guide`:导向图(支持 8 位/32 位浮点型、单通道/3 通道),**核心作用是提供图像的边缘结构信息**,决定滤波过程中的权重分配逻辑。通常选用待处理图像的纯净原图(无噪声),也可选用与输入图像尺寸一致的其他图像(如用于抠图、增强的辅助图),导向图的边缘会被精准保留到滤波结果中。 * `src`:待滤波的输入图像(支持 8 位/32 位浮点型、单通道/3 通道),即需要去噪、平滑的目标图像(如带高斯噪声的图像),要求与 `guide` 图像的尺寸(高、宽)完全一致,通道数可相同或不同(单通道与 3 通道可互相匹配)。 * `radius`:滤波窗口半径,控制局部平滑的范围(窗口大小为 `2*radius+1`)。值越大,平滑去噪效果越强,同时处理速度越慢;值越小,图像细节保留越完整,去噪效果越弱,通常设为 3/5/7(实验中常用 5)。 * `eps`:正则化参数(浮点型,通常为较小值,如 `0.01*255*255`),**核心作用是避免局部窗口内图像方差过小时出现计算不稳定(分母为 0)的问题**,同时调节保边与平滑的平衡。值越小,保边效果越锐利,边缘细节保留越精准;值越大,平滑效果越强,边缘可能出现轻微模糊。 > 滤波核心逻辑:基于「局部线性模型」,假设待滤波图像 `src` 在导向图 `guide` 的局部窗口内与 `guide` 呈线性关系,通过拟合线性系数实现平滑去噪,同时依托 `guide` 的边缘结构,避免边缘被模糊,最终实现"无伪影、高精度"的保边去噪。 **补充说明** 1. 该函数来自 OpenCV 的扩展模块 `ximgproc`,并非核心模块函数,使用前需安装 `opencv-contrib-python` 库(不可仅安装 `opencv-python`),否则会出现模块找不到的报错。 2. 处理彩色图像时,`guide` 和 `src` 均可直接输入 OpenCV 读取的 BGR 格式图像,函数返回结果仍为 BGR 格式,可视化前需通过 `cv2.cvtColor()` 转换为 RGB 格式。 3. 对高斯噪声、泊松噪声均有优异效果,保边性能优于双边滤波,且无振铃伪影,适合高精度计算机视觉任务(如图像去雾、抠图、边缘增强、工业检测图像预处理)。 4. 日常使用中,`eps` 常采用 `k*255*255` 的形式设置(k 取 0.001\~0.01),将参数归一化到 0-255 色域,更便于调参和效果控制。 5. 函数返回值为滤波后的图像,数据类型与输入图像 `src` 保持一致(8 位/32 位浮点型),若为浮点型结果,后续可视化或保存前需通过 `np.clip()` 裁剪至 0-255 并转换为 `uint8` 格式。 ##### 6. 总结 导向滤波是一种**高精度边缘保留滤波算法**,核心价值在于解决了传统滤波(如高斯滤波、双边滤波)在保边去噪过程中的痛点,凭借优异的性能在高精度图像处理领域占据重要地位 1. **算法基础**:基于「局部线性模型」构建,以导向图(通常为纯净原图)为核心参考,拟合待滤波图像与导向图的局部线性关系,实现"平滑噪声"与"保留边缘"的平衡。 2. **核心逻辑**:通过导向图提供清晰的边缘结构信息,决定滤波过程中的权重分配,在噪声区域实现强平滑去噪,在边缘区域精准保留结构细节,无额外伪影产生。 3. **关键参数** :核心依赖「窗口半径(radius)」和「正则化参数(eps)」,`radius`控制去噪平滑程度,`eps`避免计算不稳定并调节边缘锐利度,日常使用中`eps`常以`k*255*255`(k∈0.001\~0.01)的形式设置,更便于调参。 **适用场景** 导向滤波的核心优势决定了它更适合**对图像细节要求严苛的高精度图像处理场景**,典型应用包括: 1. 高精度图像去噪(如人像精修、科研图像预处理、工业检测图像去噪); 2. 图像优化类任务(如图像去雾、阴影去除、边缘增强、图像平滑美化); 3. 高级图像处理任务(如前景抠图、图像融合、超分辨率重建辅助处理)。 #### 非线性滤波对比表格 | 滤波算法 | 核心函数(OpenCV) | 核心优势 | 主要短板 | 适用噪声类型 | 典型适用场景 | |------|-------------------------------|---------------------------------|---------------------------|------------|------------------------| | 双边滤波 | `cv2.bilateralFilter()` | 保边去噪兼顾,实现简单,调参便捷 | 易残留噪声,存在轻微振铃伪影,处理速度较慢 | 高斯噪声 | 日常图像美化、人像磨皮、普通场景去噪 | | 导向滤波 | `cv2.ximgproc.guidedFilter()` | 保边精度极高,无振铃伪影,计算稳定,可拓展性强(抠图/去雾等) | 依赖扩展库,处理大图像速度慢,窗口半径越大效率越低 | 高斯噪声、泊松噪声 | 高精度图像去噪、工业检测、图像融合、前景抠图 | | 中值滤波 | `cv2.medianBlur()` | 对椒盐噪声去除效果优异,计算简单、速度快 | 易模糊图像细节,破坏边缘结构,对高斯噪声效果差 | 椒盐噪声(脉冲噪声) | 图像去椒盐噪声、消除图像中的孤立亮点/暗点 | ### Ⅳ、图像滤波总结 * 快速选型:先看图片是什么噪声 ------ 有白点黑点(椒盐噪声)就用中值滤波;有模糊噪点(高斯 / 泊松噪声),普通修图用双边滤波,专业高精度处理用导向滤波;要是只是想简单磨平、不讲究细节,用均值或高斯滤波就行。 * 线性和非线性滤波:想快、不挑效果,就用线性滤波(均值 / 高斯);想修图后保留图片轮廓、不模糊边缘,还得把噪点去掉,就用非线性滤波(中值 / 双边 / 导向),平时做专业修图也大多用这种。 * 复杂情况:如果图片又有白点黑点,又有模糊噪点,就组合着用,比如先用中值滤波去掉白点黑点,再用导向滤波精修细节,既去干净噪点,又能保住图片原本的样子。 | 滤波类型 | 算法名称 | OpenCV 核心函数 | 函数原型(简化版) | 关键参数说明 | |-------|------|-------------------------------|-------------------------------------------------------|-----------------------------------------------------------| | 线性滤波 | 均值滤波 | `cv2.blur()` | `cv2.blur(src, ksize)` | `src`:输入图像;`ksize`:滤波核大小(如`(3,3)`、`(5,5)`,需为奇数) | | 线性滤波 | 高斯滤波 | `cv2.GaussianBlur()` | `cv2.GaussianBlur(src, ksize, sigmaX)` | `src`:输入图像;`ksize`:高斯核大小(奇数);`sigmaX`:X方向高斯标准差(控制平滑程度) | | 非线性滤波 | 中值滤波 | `cv2.medianBlur()` | `cv2.medianBlur(src, ksize)` | `src`:输入图像;`ksize`:滤波核大小(奇数,如3、5,无需括号) | | 非线性滤波 | 双边滤波 | `cv2.bilateralFilter()` | `cv2.bilateralFilter(src, d, sigmaColor, sigmaSpace)` | `src`:输入图像;`d`:邻域直径;`sigmaColor`:值域标准差;`sigmaSpace`:空间标准差 | | 非线性滤波 | 导向滤波 | `cv2.ximgproc.guidedFilter()` | `cv2.ximgproc.guidedFilter(guide, src, radius, eps)` | `guide`:导向图;`src`:待滤波图;`radius`:窗口半径;`eps`:正则化参数 | * 应用场景对照 * | 滤波类型 | 算法名称 | 典型应用场景 | 场景描述 \& 使用理由 | |-------|------|---------------------------------------------------------------------|------------------------------------------------------------------------------------| | 线性滤波 | 均值滤波 | 1. 低要求图像快速平滑 2. 边缘检测前的粗略去噪 3. 消除图像中的微小均匀噪点 | 适合对图像细节无要求的场景,比如批量处理低清图片的简单磨平;理由是计算速度最快、实现最简单,能快速达到基础平滑效果。 | | 线性滤波 | 高斯滤波 | 1. 照片轻微磨皮(无保边要求) 2. 计算机视觉预处理(如特征提取前) 3. 消除图像中的轻微高斯噪声 | 适合需要均匀平滑、不希望出现块效应的场景,比如普通自拍照的简单美化;理由是平滑效果自然,相比均值滤波不易产生人工块感,且计算高效。 | | 非线性滤波 | 中值滤波 | 1. 老照片修复(去除斑点、白点/黑点) 2. 摄像头采集图像去椒盐噪声 3. 扫描文档消除孤立墨点/空白点 | 专门针对椒盐噪声(脉冲噪声)的场景,比如修复泛黄老照片上的霉点、去除监控画面中的亮点干扰;理由是对椒盐噪声去除效果最优,且计算速度较快。 | | 非线性滤波 | 双边滤波 | 1. 日常人像美化、磨皮(保留五官边缘) 2. 风景照去噪(保留山峦、树木等边缘) 3. 普通精度的产品图片修图 | 适合普通日常修图场景,需要去噪同时保留核心边缘结构,比如朋友圈照片美化;理由是无需扩展库、调参便捷,能平衡去噪与保边,效果符合日常视觉需求。 | | 非线性滤波 | 导向滤波 | 1. 高精度工业检测图像预处理 2. 专业人像精修、商业大片后期 3. 图像去雾、前景抠图、图像融合 4. 科研图像(医学、天文)去噪 | 适合对图像精度要求严苛的专业场景,比如工业零件缺陷检测、商业海报修图、医学影像分析;理由是保边精度极高无伪影,可拓展多种高级任务,能满足专业级的细节保留与去噪需求。 | #### 上一章 > [卷积:彻底搞懂卷积核怎么扫图和计算【计算机视觉】https://blog.csdn.net/R_Feynman_/article/details/156833752?spm=1001.2014.3001.5501](https://blog.csdn.net/R_Feynman_/article/details/156833752?spm=1001.2014.3001.5501)