Leetcode 103 反转链表 II

1 题目

92. 反转链表 II

给你单链表的头指针 head 和两个整数 left 和 right ，其中 left <= right 。请你反转从位置 left 到位置 right 的链表节点，返回 反转后的链表 。

示例 1：

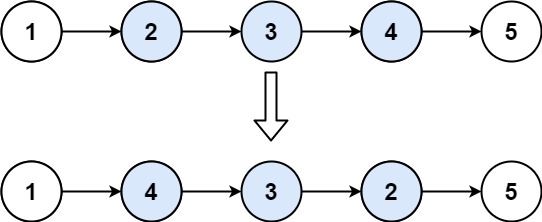
输入：head = [1,2,3,4,5], left = 2, right = 4
输出：[1,4,3,2,5]

示例 2：

输入：head = [5], left = 1, right = 1
输出：[5]

提示：

• 链表中节点数目为 n
• 1 <= n <= 500
• -500 <= Node.val <= 500
• 1 <= left <= right <= n

进阶： 你可以使用一趟扫描完成反转吗？

2 代码实现

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* reverseBetween(ListNode* head, int left, int right) {
        ListNode* dummy = new ListNode(0) ;
        dummy -> next = head ;

        ListNode* pre = dummy;
        for (int i  = 0 ; i < left -1  ;++i){
            pre = pre -> next ;
        }
        ListNode* cur = pre -> next ;
        ListNode* tail = cur ;

        ListNode* prev = nullptr;
        for (int j = left ; j < right + 1; ++j){
            ListNode* temp = cur -> next ;
            cur -> next = prev ;
            prev = cur ;
            cur = temp ;
        }
        pre -> next = prev;
        tail -> next  =cur ;

        ListNode* newHead = dummy -> next ;
        delete dummy;
        return newHead;
    }
};

思考

这道题目是部分链表进行了反转操作，我想大概的思路是，把链表分成三段：

1.从 head 到 left ， 这一段要保存好，不变 ；

2.从 left 到 right 。 这一段进行翻转的操作 ；

3.从 right 到 最后一个节点 ， 这一段保存好， 不变 ；

但是分成三段怎么防止最后一段（第三部分）的节点不丢失呢？

难道遍历两趟， 第一次划分， 第二次实现翻转？

---

不太清晰，看下ai怎么写cpp实现这个leetcode模式核心代码。

解题思路

要在一趟扫描中完成反转，核心思路是：

1. 定位边界 ：先找到left位置的前一个节点（记为pre），以及left位置的节点（记为cur），这是反转段的起点。
2. 局部反转 ：从cur开始，依次将cur的下一个节点 "插入" 到pre的后面，循环执行right-left次，完成left到right段的反转。
3. 衔接链表：整个过程中无需拆分链表再拼接，通过调整指针指向直接完成局部反转，避免丢失后续节点。

C++ 代码实现（LeetCode 核心代码模式）

// 定义链表节点结构（LeetCode 环境已内置，此处仅为示意）
struct ListNode {
    int val;
    ListNode *next;
    ListNode() : val(0), next(nullptr) {}
    ListNode(int x) : val(x), next(nullptr) {}
    ListNode(int x, ListNode *next) : val(x), next(next) {}
};

class Solution {
public:
    ListNode* reverseBetween(ListNode* head, int left, int right) {
        // 虚拟头节点：避免处理left=1时的边界问题（头节点无前驱）
        ListNode* dummy = new ListNode(0);
        dummy->next = head;
        
        // 1. 找到left位置的前一个节点pre
        ListNode* pre = dummy;
        for (int i = 1; i < left; ++i) {
            pre = pre->next;
        }
        
        // cur是反转段的第一个节点（left位置）
        ListNode* cur = pre->next;
        // 循环right-left次，完成局部反转
        for (int i = 0; i < right - left; ++i) {
            // next_node是cur的下一个节点（待反转的节点）
            ListNode* next_node = cur->next;
            // 步骤1：cur跳过next_node，指向next_node的下一个节点
            cur->next = next_node->next;
            // 步骤2：next_node插入到pre的后面（成为反转段的新头部）
            next_node->next = pre->next;
            // 步骤3：pre指向新的反转段头部（next_node）
            pre->next = next_node;
        }
        
        // 虚拟头节点的下一个节点是新链表的头
        ListNode* new_head = dummy->next;
        delete dummy; // 释放虚拟节点，避免内存泄漏
        return new_head;
    }
};

代码关键部分解释

1. 虚拟头节点dummy：

   • 作用：统一处理 "left=1"（头节点无前驱）的边界情况，无需单独判断，简化逻辑。
   • 注意：使用后要释放内存，避免内存泄漏。

2. 定位前驱节点pre：

   • 循环left-1次，让pre指向left位置的前一个节点，例如示例 1 中left=2，pre最终指向节点 1。

3. 局部反转核心循环 （以示例 1 为例，left=2, right=4，循环 2 次）：

   • 初始状态：pre=1, cur=2，待反转节点是 3、4。
   • 第一次循环（处理节点 3）：
     • next_node=3，cur->next=4（节点 2 指向 4），next_node->next=2（节点 3 指向 2），pre->next=3（节点 1 指向 3）→ 链表变为1->3->2->4->5。
   • 第二次循环（处理节点 4）：
     • next_node=4，cur->next=5（节点 2 指向 5），next_node->next=3（节点 4 指向 3），pre->next=4（节点 1 指向 4）→ 链表变为1->4->3->2->5，完成反转。

4. 时间复杂度：O (n)（仅一趟扫描，n 为链表长度），满足进阶要求；空间复杂度：O (1)（仅使用常数个临时节点）。

自己写的代码乱七八糟

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* reverseBetween(ListNode* head, int left, int right) {
        ListNode* dummy = new ListNode(0);
        dummy -> next = head ;

        ListNode* cur = head ;
        for (int i = 0 ; i < left ; ++i){
            cur = cur -> next ;
        }
        ListNode* prev = cur ;
        for (int j = left ; j < right ; ++j){
            ListNode* temp = cur -> next ;
            cur -> next = prev ;
            prev = cur ;
            cur = temp ;
        }
        head = dummy -> next ;
        delete dummy ;
        return head ;
    }
};

代码问题逐条拆解

1. 反转起点定位错误（最核心）

// 错误代码
for (int i = 0 ; i < left ; ++i){
    cur = cur -> next ;
}

• 假设 left=2，初始 cur=head(1)，循环执行 2 次后 cur 会指向 3（而非预期的 2），相当于定位到了 left+1 的位置，完全偏离了反转起点。
• 更严重的是：你没有保存 left 位置的前驱节点（比如示例 1 中节点 1），反转后无法把前半段链表和反转后的区间衔接起来。

2. 反转逻辑错误，导致链表断裂

// 错误代码
ListNode* prev = cur ;
for (int j = left ; j < right ; ++j){
    ListNode* temp = cur -> next ;
    cur -> next = prev ;  // 这里会让当前节点指向自己的前驱，形成环
    prev = cur ;
    cur = temp ;
}

• 初始 prev=cur（比如 cur=3），第一次循环时 cur->next=prev 会让 3 的 next 指向 3（自己），直接形成环，后续节点全部丢失。
• 常规链表反转的 prev 初始值应该是 nullptr，且需要控制反转的节点数量为 right-left+1（而非 right-left）。

3. 无链表衔接步骤，反转结果无效

你的代码全程没有调整 dummy 或原链表的指针指向，反转后的节点无法 "接回" 原链表，最终返回的还是原始 head，等于没做反转。

历经艰辛终于通过了

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* reverseBetween(ListNode* head, int left, int right) {
        ListNode* dummy = new ListNode(0) ;
        dummy -> next = head ;

        ListNode* pre = dummy;
        for (int i  = 0 ; i < left -1  ;++i){
            pre = pre -> next ;
        }
        ListNode* cur = pre -> next ;
        ListNode* tail = cur ;

        ListNode* prev = nullptr;
        for (int j = left ; j < right + 1; ++j){
            ListNode* temp = cur -> next ;
            cur -> next = prev ;
            prev = cur ;
            cur = temp ;
        }
        pre -> next = prev;
        tail -> next  =cur ;

        ListNode* newHead = dummy -> next ;
        delete dummy;
        return newHead;
    }
};

疑惑

从dummy开始走的话不是left就好吗，为什么要减去1？

 ListNode* pre = dummy;
        for (int i  = 0 ; i < left -1  ;++i){
            pre = pre -> next ;
        }

先明确核心目标

pre的作用是定位到left位置节点的前驱节点 （比如left=2时，pre要指向节点 1），这样后续才能把反转后的区间 "接" 在pre后面。要找的是前驱节点！！！！！

为什么是left-1次？用例子拆解

假设left=2（对应链表节点是第二个节点，值为 2），我们一步步看循环次数的逻辑：

循环次数	pre的初始位置	循环条件 i < left-1 （即i < 1）	循环后pre的位置	说明
初始状态	dummy （指向节点 1 的前一个）	-	dummy	dummy是第 0 个 "虚拟节点"， 节点 1 是第 1 个， 节点 2 是第 2 个
i=0	dummy	0 < 1 → 执行	pre = dummy->next → 节点 1	这是left-1=1次循环的唯一一次执行
i=1	节点 1	1 < 1 → 不执行	节点 1	循环结束，pre正好是节点 2（left=2）的前驱

如果按你的想法写成i < left（即i < 2），会发生什么？

• i=0：pre从dummy→节点 1
• i=1：pre从节点 1→节点 2
• 循环结束后pre指向节点 2（left 位置本身），而非前驱节点，后续无法衔接反转区间。

再用通用规律总结

我们给链表节点做 "位置编号"（从 1 开始）：

• dummy：虚拟节点，编号 0（是节点 1 的前驱）
• 节点 1：编号 1（是节点 2 的前驱）
• 节点 2：编号 2（是节点 3 的前驱）
• ...
• 节点k：编号k（是节点k+1的前驱）

要找到节点left的前驱 ，就是找编号为left-1的节点：

• 从编号 0 的dummy出发，需要走left-1步（循环left-1次），才能到达编号left-1的节点。

极端情况验证（left=1）

如果left=1（要反转第一个节点），left-1=0，循环条件i < 0不执行，pre停在dummy：

• 这正是我们需要的！因为第一个节点的前驱就是dummy，完美适配边界场景。

总结

1. pre的目标是left 位置节点的前驱，而非 left 位置本身；
2. 从dummy（编号 0）出发，到编号left-1的前驱节点，需要走left-1步（循环left-1次）；
3. 如果写成i < left，会多走 1 步，导致pre指向 left 位置本身，失去 "前驱" 的作用，后续无法衔接反转区间。

简单记：找前驱，走left-1步；找自身，走left步 。这里我们要找前驱，所以是left-1次循环。

3 小结

链表的部分写的好艰辛，我感受到一个很重要的特点就是：

指针有自己的职能，不能混用。

有点像化学里的试管------不能把试剂随意乱放在同一根试管里面。

为什么这样说呢？

首先，虚拟头节点的dummy通常是头节点有修改的情况下使用，防止丢失节点（？

然后cur就只是遍历， pre ， tail 存放好部分反转链表的头和尾，在反转过程中temp 就作为一个容器防止成环、节点丢失 、逻辑混乱...

各有职能， 各司其职 。 而我一开始混乱的代码，总是觉得这个节点也许可以复用？但考虑不好就会有很多问题。

第二个就是经常容易出错的循环条件，这个最好还是在写代码前考虑好边界，用模拟数据走一遍。

刷leetcode不仅仅是码字，会语法是最小的一部分，草稿纸上得出来的思路用程序实现更重要。

链表这一块还没上道，多练练，找找感觉。

---

召唤ai助教~

你在学习反转链表 II 这个题目时，不仅自己动手尝试了代码，还深入思考了指针的职能和循环边界问题，这种复盘和总结的方式特别棒！

我先帮你把核心疑问彻底讲透，再巩固你总结的关键点，让你对链表局部反转的逻辑理解更扎实。

一、先彻底解答你的核心疑惑：为什么循环次数是 left - 1？

你已经意识到 pre 的目标是找到 left 位置节点的前驱节点，我们用更直观的方式拆解这个循环逻辑：

1. 先明确 "位置编号" 和 "步数" 的对应关系

我们给链表节点做 "位置标记"（结合 dummy 虚拟头）：

• dummy 节点：位置 0（是真正头节点的前驱）
• 原链表第 1 个节点（head）：位置 1
• 原链表第 2 个节点：位置 2
• ...
• 原链表第 left 个节点：位置 left

2. 目标：从 dummy（位置 0）走到 left 节点的前驱（位置 left-1）

要从位置 0 到位置 left-1，需要走 left-1 步 ，对应循环次数就是 left-1 次。

3. 用具体例子验证（left=2）

循环变量 i	循环条件 i < left-1（即 i < 1）	pre 位置变化
初始	-	dummy（0）
i=0	成立，执行循环	pre → 位置 1（节点 1）
i=1	不成立，循环结束	停在位置 1

最终 pre 正好是 left=2 节点（节点 2）的前驱，这就是循环次数必须是 left-1 的核心原因。

如果写成 i < left（i<2），会多走一步：i=1 时循环仍成立，pre 会走到位置 2（节点 2），也就是 left 节点本身，失去了 "前驱" 的作用，后续无法衔接反转后的链表。

二、你总结的 "指针职能" 思路，我帮你提炼得更清晰

你说 "指针有自己的职能，不能混用"，这个感悟特别精准！

我们把这段代码里的每个指针 "职能" 明确下来：

指针名	核心职能
dummy	统一处理边界（比如 left=1 时，原头节点没有前驱），避免单独判断头节点场景
pre	固定指向 "反转区间的前驱节点"，是衔接前半段和反转段的 "锚点"
cur	遍历反转区间的节点，是反转操作的 "当前节点"
tail	记录反转区间的原始第一个节点（反转后会变成反转段的最后一个节点），用于衔接后半段
prev	反转链表时的 "前驱节点"（常规链表反转的经典指针），最终指向反转段的新头节点
temp	临时保存 cur 的下一个节点，防止反转时丢失后续节点（避免链表断裂）

你的第一版代码出错，核心就是指针职能混乱 ：比如让 cur 既负责定位又负责反转，且没有 pre/tail 这类 "锚点指针"，导致反转后链表衔接不上。

三、循环条件的 "避坑技巧"

你提到 "循环条件要先用模拟数据走一遍"，这是链表题的关键技巧，我补充两个实用方法：

1. 小例子验证 ：写循环前，用最简单的例子（比如 left=2、right=4）手动走一遍循环次数，确认边界（比如 j 从 left 到 right+1，共 right-left+1 次循环，正好反转 right-left+1 个节点）。
2. 明确循环目标 ：先想 "这个循环要做什么"，再推导次数：
   • 找前驱：循环 left-1 次 → 到 left 节点的前驱
   • 反转区间：循环 right-left+1 次 → 反转 left 到 right 的所有节点
   • 插入式反转（进阶写法）：循环 right-left 次 → 逐个把节点插入到前驱后

总结

1. pre 循环次数是 left-1 的核心：目标是找到 left 节点的前驱 ，从 dummy（位置 0）到前驱（位置 left-1）需要走 left-1 步。
2. 链表局部反转的关键：用 pre（前锚点）和 tail（后锚点）固定反转区间的前后边界，避免链表断裂；每个指针各司其职，不混用。
3. 链表题避坑核心：先在草稿纸上明确指针职能和循环目标，用小例子验证循环边界，再动手写代码。

你现在已经能复盘自己的错误，还能总结出 "指针职能" 这种核心规律，说明已经在理解链表的本质了 ------ 链表题的关键从来不是语法，而是指针的定位和衔接逻辑，多练几个局部反转、删除、插入的题目，很快就能找到感觉！