现在感觉,神经网络模型成为了基本单元,或者原理图的元器件,或者积木的基本块,然后人们设计出各种类型的积木块(自己想怎么设计就怎么设计),用这些积木进行搭建,CNN呀,RNN,transformer等诞生了。
CNN 的英文全称是 Convolutional Neural Network,中文译为卷积神经网络。
CNN分成卷积层、池化层和全连接层。
卷积层:特征提取。
池化层:降维。
全连接层:输出结果。
1.组成
1.1 卷积层
功能:网络的核心,用于特征提取。
关键概念:
卷积核/滤波器(filter) :一个小的权重矩阵(如3x3, 5x5)。以前把filter翻译为滤波器,现在都是翻译成卷积核。
这个和全连接神经网络(FC)不同的是,不再一个输入点一个权重了,人类真聪明,改成了一组权重(减少了权重个数),引入卷积计算,所有输入共享这组权重,如果还是一个输入一个权重,很庞大的参数量,又结合人类眼睛关注的就是一片一片的------人的奇思妙想就是这样------创建AI又用AI又关注自身的大脑神经网络(研究自身)。
它在输入上滑动,计算局部点积,生成特征图。一个卷积层可以有多个不同的卷积核,每个负责提取一种特征。
特征图(feature map):卷积核在输入上滑动计算后得到的输出。它反映了原图中某种特征(如垂直边缘)的分布。
步长(stride):卷积核每次移动的像素数。步长大,输出尺寸小。
填充(padding):在输入图像边缘补零。目的是控制输出特征图的尺寸,防止过快缩小。还有一点原因是如果不填充,通过卷积核扫描计算,它边界(上下左右)的元素被扫描的少,采样和中心的元素相比就有损失,所以就填充(padding),把边缘信息多采样几次,获取更多的信息。
注意:
(1)填充是一圈一圈的填充。
(2)卷积核通道数和特征图通道数。
一个卷积核的通道数由输入的通道数决定 。
比如卷积核我们设置大小为mxn,输入通道为3,那么一个卷积核就是mxnx3。同时,一个卷积核生成一个特征图------啥意思呢?设置卷积核为1个(超参数),那么就算输入数据是3个通道,也只是决定卷积核是由3个通道的权重矩阵组成(即3个权重矩阵,每个通道对应一个),但是特征图通道为1------即一个特征矩阵------因为卷积运算就是各个输入通道矩阵和卷积核对应的通道矩阵进行点积计算,会有3个结果(每个通道一个),然后这3个结果相加就是对应特征图的对应元素。
另外如果输入通道是1个的话,那说明卷积核就只有一个通道(即一个权重矩阵),如果设置卷积核为1,则输出特征图也是一个通道的话是1。
如果你设置h个卷积核,那么特征图才是L个通道(就是h个特征矩阵组成)。
就是说不管你输入通道有多少个,卷积核有几个才会生成几个特征图。也就是说卷积核的个数决定特征图的通道数。
1.1.1 特征图尺寸计算公式
特征图尺寸计算公式如下:
输出尺寸 = (输入尺寸 + 填充×2 - 卷积核尺寸) ÷ 步长 + 1
输入尺寸:高(行)或宽(列)。
卷积核尺寸:高(行)或宽(列)。
这是2维,三维再说。
比如输入尺寸是64x128(高x宽),步长设为1,填充为1,卷积核尺寸是3x5,那么特征图是多少呢?如下计算过程:
高(行):(64+1x2-3)/1+1=64
宽(列):(128+1x2-5)/1+1=126
因此特征图尺寸是64x126。
这是取的特殊情况,一般卷积核尺寸是正方形,也就是高宽(行列)都是一样的。
经过实践检验(看来,深度学习还真是实验科学),目前有3类卷积:
(1)普通卷积(常用)
参数: 卷积核=3(即3x3的意思), 步长=1, 填充=1
结果:尺寸不变!输入多大,输出就多大
举例: 224×224 → 卷积后还是 224×224
(2)下采样卷积(缩小尺寸)
参数: 卷积核=3(即3x3的意思), 步长=2, 填充=1
结果:尺寸减半!输入除以2(大概)
举例: 224×224 → 卷积后变成 112×112
(3)最大池化(最常用缩小法)
参数: 池化核=2(即卷积核2x2的意思), 步长=2, 填充=0
结果:精确减半!
举例: 224×224 → 池化后精确变成 112×112
1.1.1 API
pytorch中的API是 torch.nn.Conv2d。
接口名是 Conv2D 的英文缩写,其全称是:Convolutional 2D。
具体拆解如下:
Conv = Convolutional(卷积)
2D = 2-Dimensional(二维)
所以 Conv2d 表示这是一个用于处理二维数据(如图像、矩阵)的卷积层。
然后你会不会问有没有1和3?当然有了!
Conv1d → 一维卷积(如时序信号)
Conv2d → 二维卷积(如图像)
Conv3d → 三维卷积(如视频/医学体积数据)
🎯 卷积家族接口一览表:
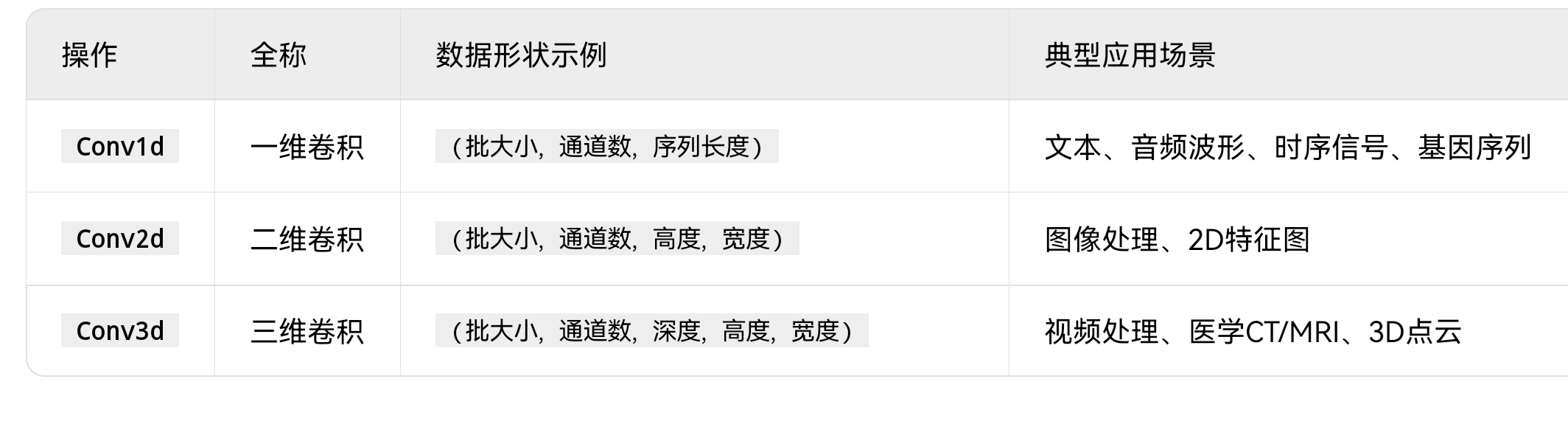
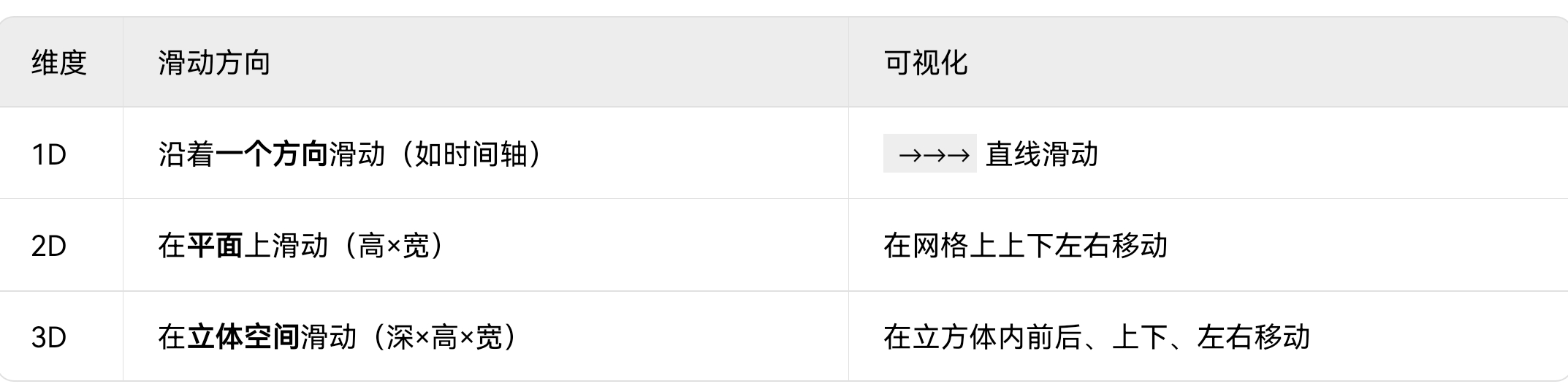
🎯 核心差异:卷积核滑动方向
🎯 通用形参(1D/2D/3D共享)
ConvNd(in_channels, out_channels, kernel_size, stride=1, padding=0, dilation=1, groups=1, padding_mode='zeros')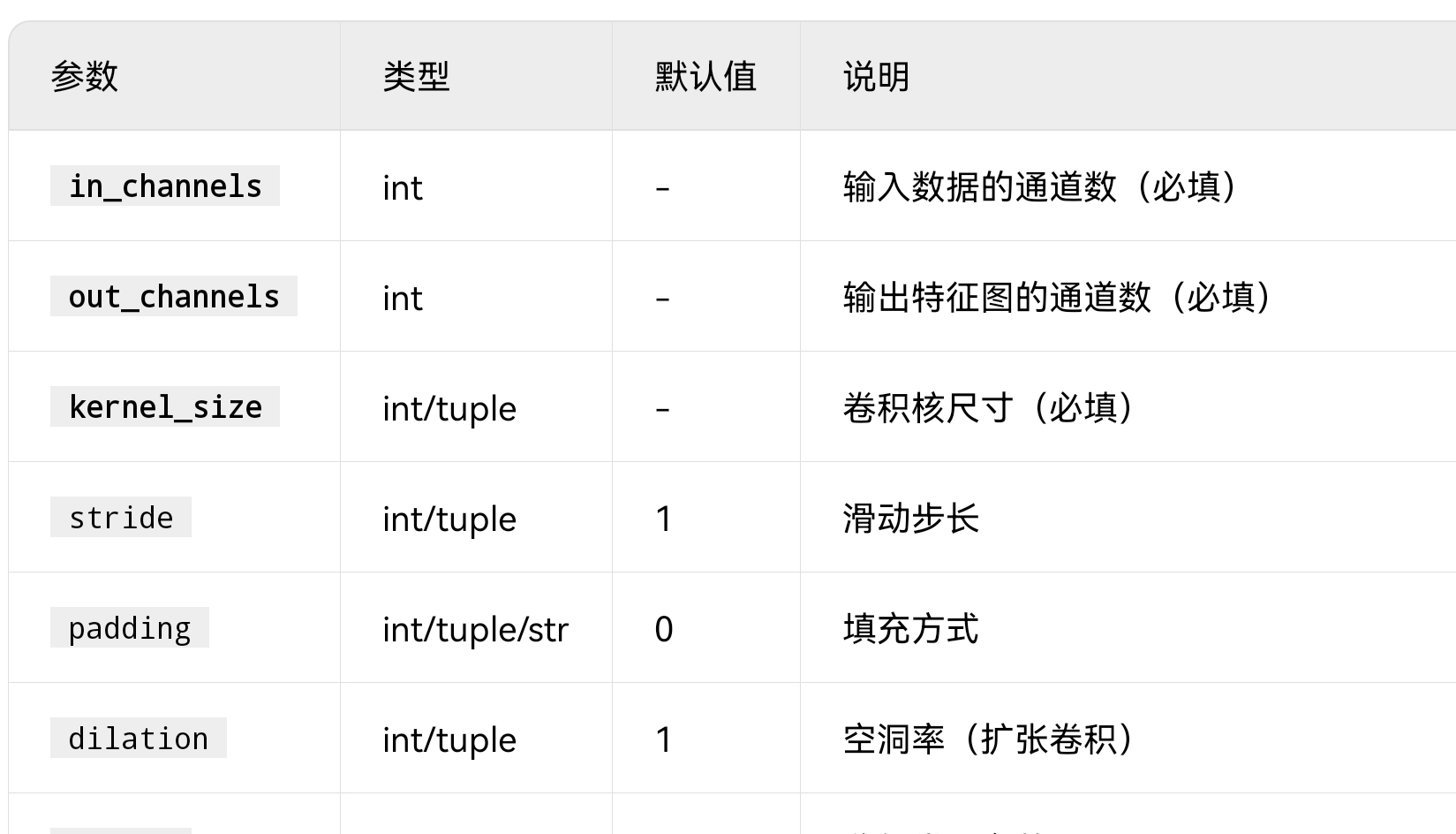
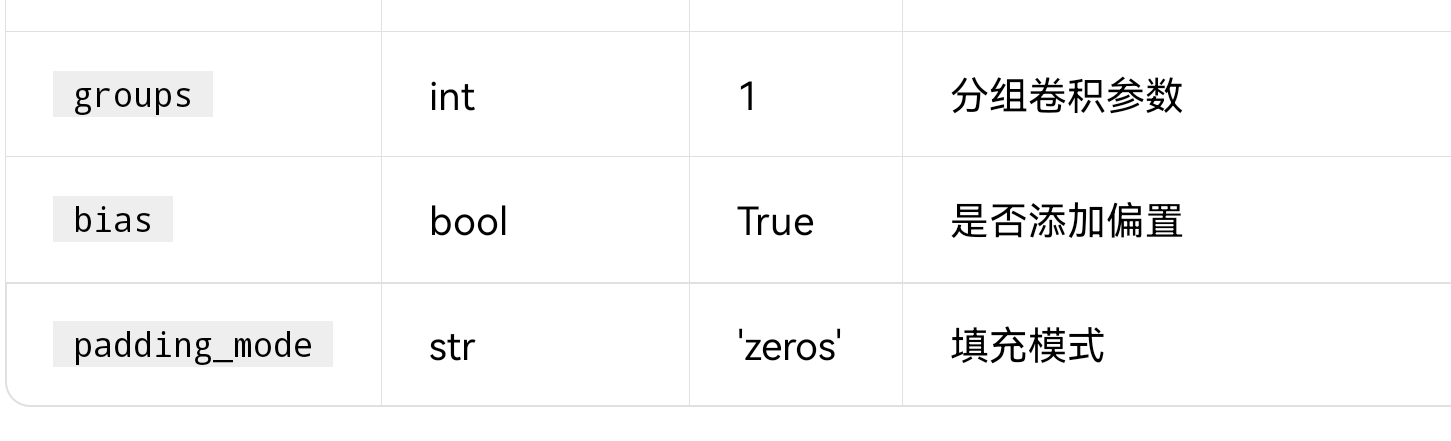
它这个API增加了感受野的功能,dilation形参来表示。
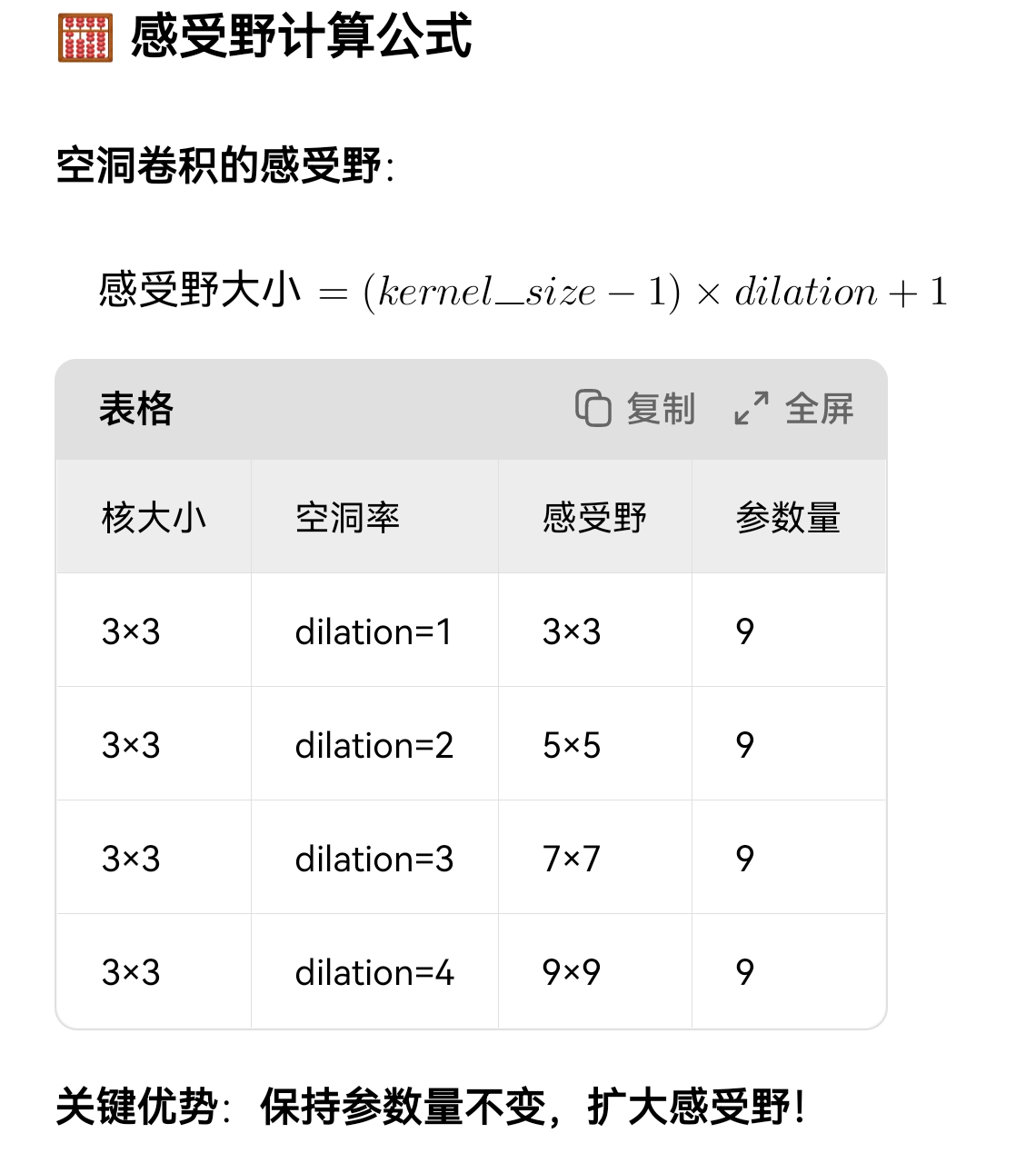

把空洞卷积想象成"带间隔的采样":
dilation=1 :正常采样,每个像素都看
dilation=2 :隔一个像素采样一次
dilation=3 :隔两个像素采样一次。
就像用放大镜看东西:镜片大小不变(参数量不变),但能看到更大的范围(感受野增大)!
其实就是采样后大小没变,只是跳着采样了!
所以,计算特征图的公式就变了 :
输出尺寸 = (输入尺寸 + 填充×2 - 感受野尺寸) ÷ 步长 + 1
当参数dilation为默认值------1------时它就又蜕变成一般的特征图公式了:
输出尺寸 = (输入尺寸 + 填充×2 - 卷积核尺寸) ÷ 步长 + 1
只是感受野尺寸成为卷积核尺寸了!!!
1.2 激活函数层
功能:引入非线性,使网络能够学习复杂的模式。
常用函数:ReLU。它将所有负值置零,保留正值。计算简单,能有效缓解梯度消失问题。
它的位置是卷积层后面加上非线性。
1.3 池化层
池化层通常紧跟在卷积层之后,其主要目的是压缩特征图,降低数据维度,同时保留最重要的信息。它是CNN能够实现平移不变性和层级特征提取的关键。
池化窗口:和卷积核概念类似,就是一个滑动窗口。
池化窗口大小:和卷积核大小一样。
步长:和卷积的步长一样。
填充:和卷积的填充一样。
池化后大小计算和卷积计算公式一样。
注意一点,和卷积计算不同的是它只是对特征图的降维,不改变特征图的通道,就是有几个通道的特征图,那么池化后还是几个通道的特征图,只是可能维度降低了。
池化计算比较简单,常用类型:
最大池化:取窗口内的最大值。最常用,能保留最显著的特征。
平均池化:取窗口内的平均值。
特点:池化操作是确定性的,没有需要学习的参数。
1.3.1 API
pytorch中最的api如下
最大池化API
torch.nn.MaxPool1d/2d/3d 分别用于1D(序列)、2D(图像)、3D(体数据)数据的最大池化,最常用的是 nn.MaxPool2d 用于图像处理
基本最大池化
maxpool = torch.nn.MaxPool2d(
kernel_size=2, # 池化窗口大小
stride=2, # 步长,默认等于kernel_size
padding=0, # 填充
dilation=1, # 扩张率
return_indices=False, # 是否返回最大值的位置(用于MaxUnpool)
ceil_mode=False # 输出尺寸计算方式,False向下取整,True向上取整
)
平均池化API
torch.nn.AvgPool1d/2d/3d。
常用2d。
avgpool = nn.AvgPool2d(
kernel_size=2,
stride=2,
padding=0,
ceil_mode=False,
count_include_pad=True # 计算均值时是否包含填充值
)
等等,还有什么自适应池化接口,在不断变化,但常用MaxPool2d
1.4 全连接层
功能:通常出现在网络的最后几层。
它将前面卷积和池化层提取到的、在空间上展开的二维高级特征"拉直"成一维向量,并进行综合,用于最终的分类或回归输出。
注意:在现代架构(如ResNet)中,常用"全局平均池化"替代一部分全连接层,以减少过拟合。
1.4.1 pytorch的API
pytorch中的API最常用的是torch.nn.Linear,如下
linear_layer = nn.Linear(
in_features=100, # 输入特征维度
out_features=50, # 输出特征维度
bias=True # 是否包含偏置项(默认True)
)
2.超参数
输入通道数,
卷积核超参数:步长,大小,个数。
一个卷积核的通道数由输入的通道数决定。
填充数。
网络层数,
激活函数,
学习率,
等等。