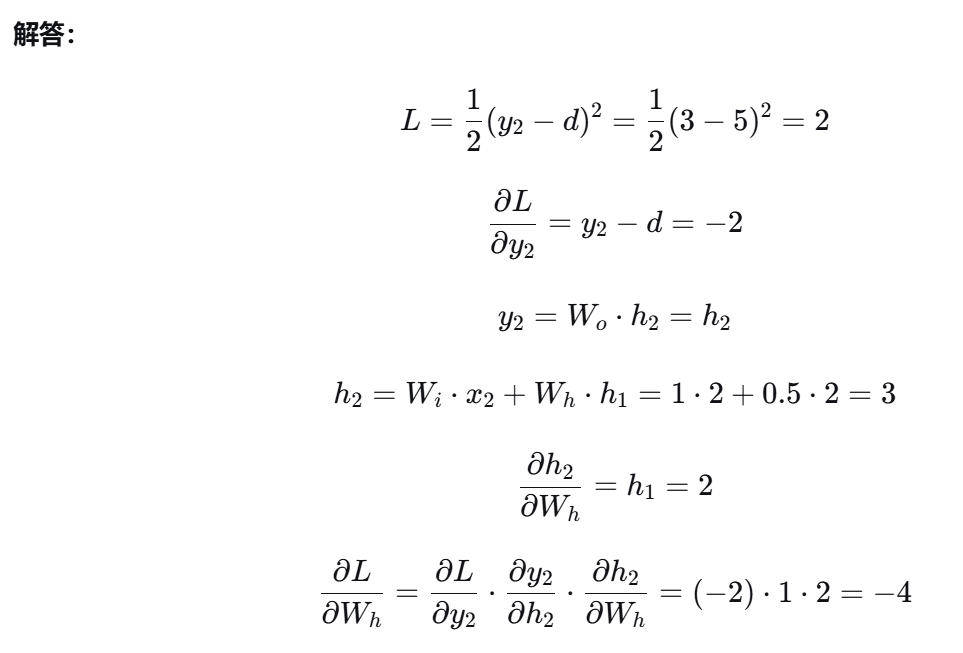一、基本概念与填空考点
-
RNN全称:循环神经网络(Recurrent Neural Network)
-
RNN的主要特点:
-
具有记忆能力,能处理序列数据
-
前后输入之间存在依赖关系
-
-
与CNN和前馈网络的区别:
-
CNN:局部感知、参数共享,用于图像
-
RNN:处理序列(如文本、语音、视频)
-
-
RNN的两种主要结构:
-
简单循环网络(SRN / Elman Network)
-
长短时记忆网络(LSTM)
-
-
LSTM的三个门结构:
-
输入门(Input Gate)
-
遗忘门(Forget Gate)
-
输出门(Output Gate)
-
-
GRU的两个门结构:
-
更新门(Update Gate)
-
重置门(Reset Gate)
-
-
RNN的训练算法:
- BPTT(沿时间反向传播)
二、结构与应用题型
-
RNN的输入输出类型:
-
一对一、一对多、多对一、多对多
-
举例:情感分类(多对一)、机器翻译(多对多)、图像描述(一对多)
-
-
RNN在NLP中的应用:
- 词性标注、情感分析、机器翻译、问答系统
-
LSTM与GRU的区别:
-
LSTM:三个门,结构复杂,记忆单元独立
-
GRU:两个门,结构简单,计算更快
-
三、计算与推导题型
-
RNN时间展开计算:
-
给定输入序列、初始隐状态、权重,能计算隐状态序列与输出序列
-
示例题型见课件中"Example: All weights are 1"部分
-
-
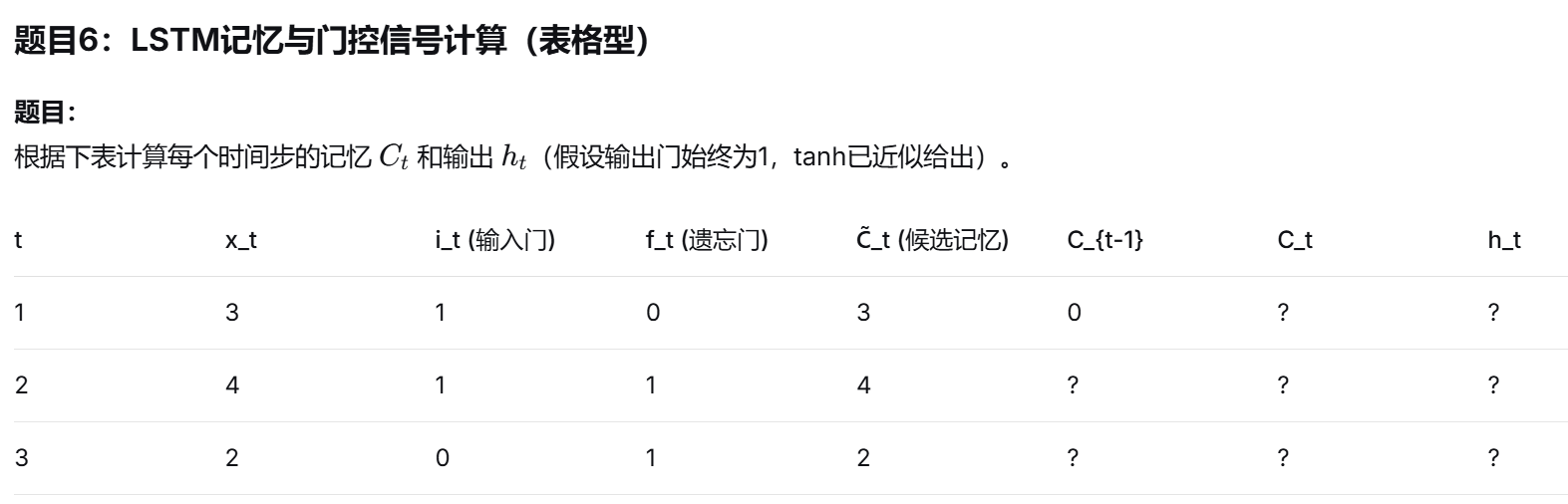
LSTM门控计算:
-
给定输入、前一状态、门控信号,能计算记忆单元更新与输出
-
课件中LSTM示例表格是典型计算题来源
-
-
梯度消失与爆炸:
-
RNN梯度消失的原因:连乘导致梯度指数衰减
-
LSTM如何缓解:通过门控机制控制信息流动
-
四、对比与简答题型
-
RNN vs CNN vs 前馈网络:
- 结构差异、适用任务差异、记忆能力差异
-
LSTM vs GRU:
- 结构差异、计算效率、适用场景
-
BPTT vs 标准BP:
-
BPTT是BP在时间维度上的展开
-
需理解梯度如何沿时间步传播
-
五、图示与流程题
-
RNN展开图:
- 能画出RNN在时间上的展开图(如课件中"Recurrent Network"图示)
-
LSTM单元结构图:
- 能标注输入门、遗忘门、输出门、记忆单元、输入输出路径
-
GRU结构图:
- 能标注更新门、重置门、隐状态传递路径
六、记忆与概念强化题
-
关键人物与模型:
-
Elman Network(1990)
-
LSTM(Hochreiter & Schmidhuber,1997)
-
GRU(Cho et al.,2014)
-
-
RNN的缺点与改进:
-
梯度消失 → LSTM/GRU
-
计算效率低 → 优化结构如GRU
-
-
RNN与递归神经网络(RecNN)的区别:
- RNN处理序列,RecNN处理树状结构
✅ 复习建议:
-
熟记RNN、LSTM、GRU的结构名称与门控机制
-
掌握序列计算题型(如课件中线性权重为1的示例)
-
理解BPTT与梯度问题的关系
-
能画出RNN、LSTM的结构示意图
-
熟悉RNN在NLP中的典型应用场景
题目2:LSTM门控信号计算(选择题型)
题目:
LSTM中,输入门、遗忘门、输出门的激活函数通常为( )函数,输出值范围在( )之间,用于模拟门的( )状态。
A. Sigmoid,[0,1],开/关
B. Tanh,[-1,1],正/负
C. ReLU,[0,∞],激活/抑制
D. Softmax,[0,1],概率分布
答案: A


🔤 填空题集
-
RNN全称是循环神经网络 ,主要用于处理序列数据。
-
RNN中用于训练的时间反向传播算法简称BPTT。
-
LSTM的三个门分别是输入门、遗忘门、输出门。
-
GRU的两个门分别是更新门、重置门。
-
RNN容易出现梯度消失 问题,LSTM通过门控机制缓解该问题。
-
Elman Network是**简单循环网络(SRN)**的一种。
-
RNN在时间维度上展开后,可看作是一个深度网络。
-
在机器翻译任务中,RNN通常采用多对多结构。
-
LSTM中遗忘门的作用是控制是否遗忘上一时刻记忆。
-
GRU相比LSTM的优点是结构简单、计算速度快。
❓ 简答题集
-
简述RNN与CNN的主要区别。
- RNN适用于序列数据,具有记忆能力;CNN适用于图像数据,具有局部感知和参数共享特性。
-
为什么RNN会出现梯度消失问题?LSTM是如何缓解的?
- RNN梯度在时间步上连乘,导致指数衰减。LSTM引入门控机制和记忆单元,可选择性地遗忘和记忆,减轻梯度衰减。
-
描述LSTM中"遗忘门"的作用。
- 遗忘门决定从上一记忆单元中保留多少信息到当前记忆单元,通过Sigmoid输出[0,1]之间的值控制遗忘程度。
-
GRU与LSTM相比,有哪些结构上的简化?
- GRU将输入门与遗忘门合并为更新门,取消独立记忆单元,将记忆与隐状态合并,结构更简洁。
-
举例说明RNN在自然语言处理中的一个应用,并描述其输入输出结构。
- 如情感分类:输入为词序列(多对一),输出为情感标签(积极/消极)。
-
画出简单RNN在三个时间步上展开的示意图,并标注输入、隐状态、输出。
- 参考课件中"Recurrent Network"展开图。
如果你还需要RNN/LSTM/GRU的结构图示复习 或更多计算变形题,我可继续整理。是否需要?
需要
以下是针对RNN/LSTM/GRU的结构图示复习要点 与更多计算变形题,适合用于图文结合复习与计算巩固:
🖼️ RNN/LSTM/GRU 结构图示复习要点
一、简单RNN(Elman Network)时间展开图
text
时间展开示意图(三个时间步):
x1 x2 x3
| | |
v v v
RNN RNN RNN
| | |
v v v
h1 ---> h2 ---> h3
| | |
v v v
y1 y2 y3
说明:
- h_t = f(W_i * x_t + W_h * h_{t-1} + b_h)
- y_t = g(W_o * h_t + b_o)
- 箭头表示隐状态传递二、LSTM单元内部结构图
text
LSTM 单元结构:
输入:
x_t (当前输入)
h_{t-1} (前一隐状态)
C_{t-1} (前一记忆)
门控信号:
i_t = σ(W_i · [h_{t-1}, x_t] + b_i) [输入门]
f_t = σ(W_f · [h_{t-1}, x_t] + b_f) [遗忘门]
o_t = σ(W_o · [h_{t-1}, x_t] + b_o) [输出门]
记忆更新:
C̃_t = tanh(W_c · [h_{t-1}, x_t] + b_c) [候选记忆]
C_t = f_t ⊙ C_{t-1} + i_t ⊙ C̃_t [新记忆]
输出:
h_t = o_t ⊙ tanh(C_t) [新隐状态]
符号说明:
σ: Sigmoid
⊙: 逐元素乘
tanh: 双曲正切三、GRU单元内部结构图
text
GRU 单元结构:
输入:
x_t (当前输入)
h_{t-1} (前一隐状态)
门控信号:
z_t = σ(W_z · [h_{t-1}, x_t] + b_z) [更新门]
r_t = σ(W_r · [h_{t-1}, x_t] + b_r) [重置门]
候选状态:
h̃_t = tanh(W_h · [r_t ⊙ h_{t-1}, x_t] + b_h)
输出:
h_t = (1 - z_t) ⊙ h_{t-1} + z_t ⊙ h̃_t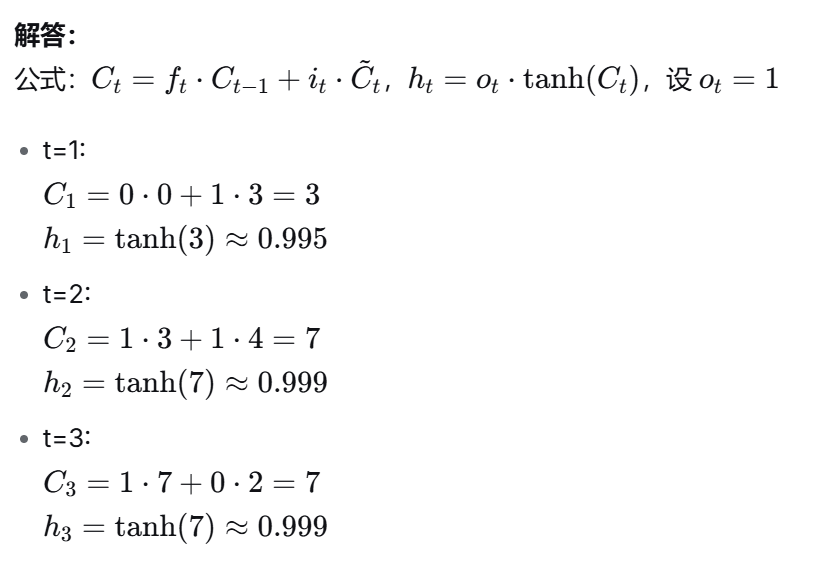
✅ 复习建议
-
画图记忆:动手画出RNN、LSTM、GRU的结构图,标注输入输出与门控。
-
计算熟练:多做门控信号、状态更新的计算题,尤其是带Sigmoid/tanh的近似计算。
-
对比理解:总结RNN、LSTM、GRU的异同,特别是如何解决梯度问题。
-
题型覆盖:填空题、计算题、简答题都要练习,尤其是结合序列数据的应用题。