数据结构第六章：图

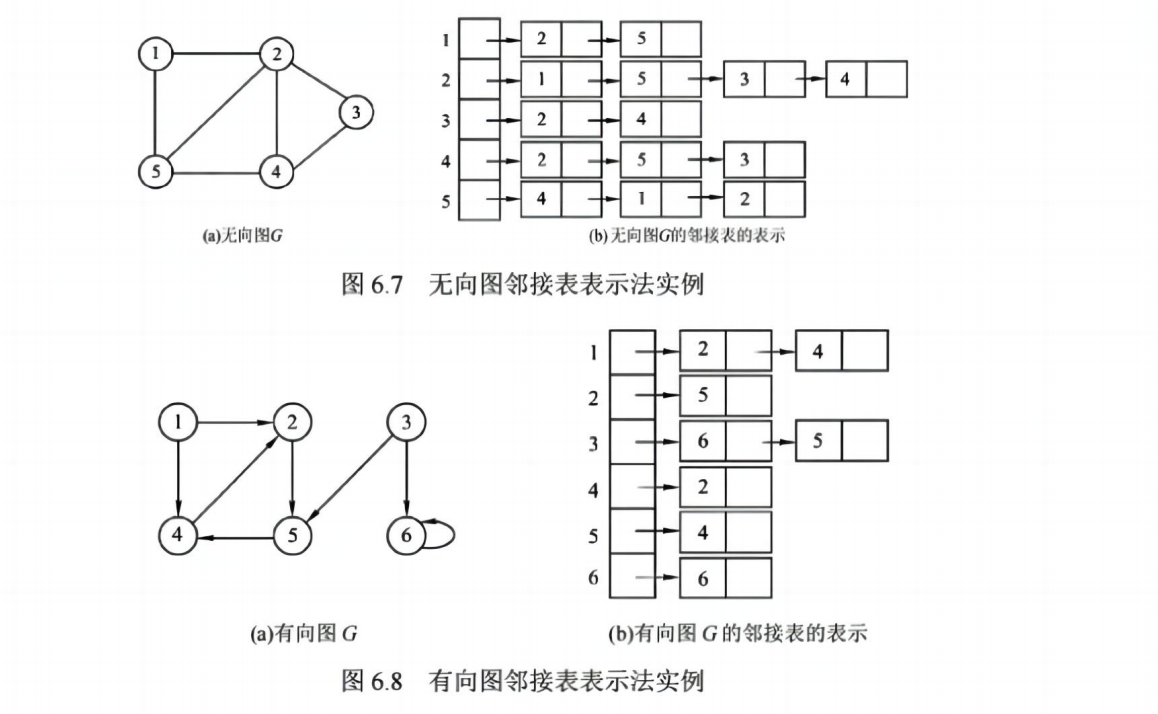
一、图的基本定义

✅ 什么是图？

图（Graph） 是由 顶点（Vertex）集合 V 和 边（Edge）集合 E 组成的一种非线性数据结构。

• 若边有方向 → 有向图
• 若边无方向 → 无向图
• 边有权重 → 带权图（网）

🔑 基本术语

术语	说明
度	顶点的边数；有向图中分为入度和出度
路径	从一个顶点到另一个顶点的顶点序列
连通图	任意两点间都有路径（无向图）
强连通图	任意两点间都有双向路径（有向图）

💡 考点：判断图的类型、计算度数、找路径长度

二、图的存储结构

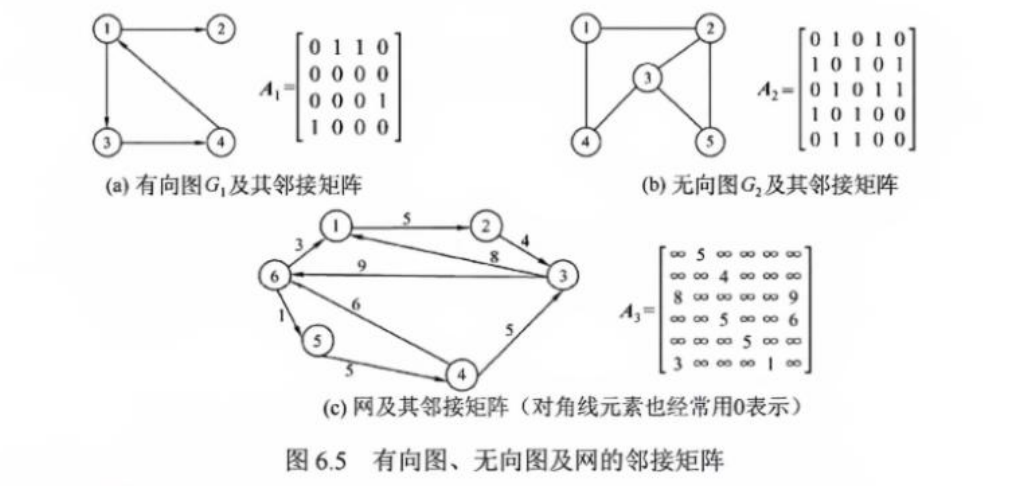
1. 邻接矩阵法（Adjacency Matrix）

• 用二维数组表示顶点间的连接关系
• matrix[i][j] = 1 表示存在边，否则为 0（或无穷大表示无边）

✅ 优点：

• 简单直观，便于判断任意两点是否相连
• 适合稠密图

❌ 缺点：

• 空间复杂度 O(n^2) ，稀疏图浪费严重
• 修改边操作较慢

✍️ 存储结构：

#define MaxVertexNum 100 // 顶点数目的最大值
typedef char VertexType; // 顶点对应的数据类型
typedef int EdgeType; // 边对应的数据类型
typedef struct {
    VertexType vex[MaxVertexNum]; // 顶点表
    EdgeType edge[MaxVertexNum][MaxVertexNum]; // 邻接矩阵，边表
    int vexnum, arcnum; // 图当前的顶点数和边数
} MGraph;

📌 考点：画邻接矩阵、判断是否连通

---

2. 邻接表法（Adjacency List）

• 每个顶点对应一个链表，存储其所有邻接顶点
• 适合稀疏图

✅ 优点：

• 存储空间节省， O(n+e)
• 遍历邻接顶点高效

❌ 缺点：

• 判断两个顶点是否直接相连需遍历链表

✍️ 存储结构：

typedef char VertexType; // 顶点对应的数据类型
#define MaxVertexNum 100 // 顶点数目的最大值
typedef struct ArcNode { // 边表结点
    int adjvex; // 该弧所指向的顶点的位置
    struct ArcNode *nextarc; // 指向下一条弧的指针
} ArcNode;

typedef struct VNode {
    VertexType data; // 顶点信息
    ArcNode *firstarc; // 指向第一条依附该结点的弧的结点
} VNode, AdjList[MaxVertexNum];

typedef struct {
    AdjList vertices; // 邻接表
    int vexnum, arcnum; // 图的顶点数和弧数
} ALGraph; // ALGraph是以邻接表存储的图类型

📌 考点：画邻接表、理解头结点与边结点

---

3. 十字链表（用于有向图）

• 结合邻接表和逆邻接表，每个边结点有两个指针
• 便于查找某顶点的出边和入边

✍️ 存储结构

🔹 弧结点（Arc Node）

弧结点用于表示一条有向边（弧） ，每个弧对应一个 headvex 和 tailvex 的关系。

域名	含义
tailvex	表示该弧的尾顶点编号 （即起点） 👉 指向这条边从哪个顶点出发。
headvex	表示该弧的头顶点编号 （即终点） 👉 指向这条边指向哪个顶点。
hlink	指向以同一头顶点 （即 headvex 相同）的下一个弧结点 👉 构成"逆邻接表"：所有指向某个顶点的边连在一起。
tlink	指向以同一尾顶点 （即 tailvex 相同）的下一个弧结点 👉 构成"邻接表"：所有从某个顶点发出的边连在一起。
(info)	可选字段，用于存储边的附加信息 ，如权重、长度等 👉 在无权图中可省略。

✅ 总结：

• tlink 实现了出边链表（从某顶点出发的所有边）
• hlink 实现了入边链表（指向某顶点的所有边）
• 这种双重链接结构使得可以快速访问某顶点的出边和入边

---

🔹 顶点结点（Vertex Node）

顶点结点用于表示图中的每一个顶点。

域名	含义
data	存储该顶点的数据信息 ，如顶点名称、值等 👉 例如：城市名、任务名等。
firstin	指向以该顶点为头顶点 的第一个弧结点（即指向它的第一条边） 👉 即该顶点的入边链表头指针。
firstout	指向以该顶点为尾顶点 的第一个弧结点（即从它发出的第一条边） 👉 即该顶点的出边链表头指针。

✅ 总结：

• firstout → 从该顶点出发的所有边（出度）
• firstin → 指向该顶点的所有边（入度）

🔹 示例图

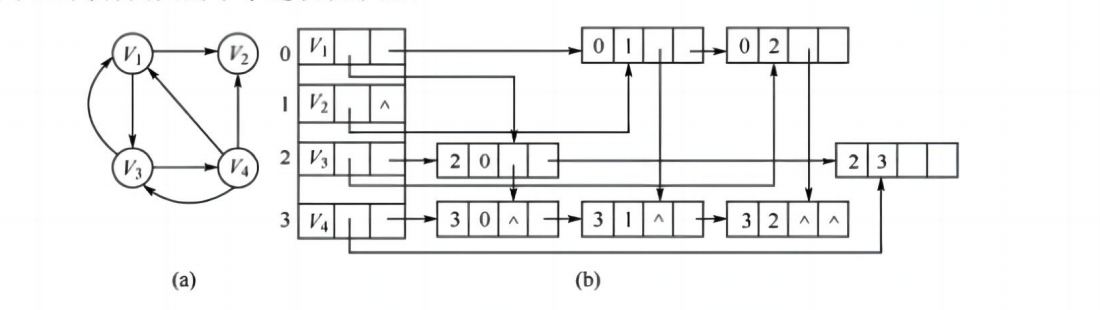
⚠️ 注：主要用途是支持有向图的边操作，近年未考

---

4. 邻接多重表（用于无向图）

• 一条边用两个边结点表示，共享同一记录
• 便于删除边（如网络拓扑）

✍️ 存储结构

🔹 边结点（Edge Node）

域名	含义
ivex	该边连接的第一个顶点的编号
jvex	该边连接的第二个顶点的编号
ilink	指向另一个与 ivex 相连的边（即从 ivex 出发的下一条边）
jlink	指向另一个与 jvex 相连的边（即从 jvex 出发的下一条边）
(info)	可选字段，存储边的附加信息（如权重）

💡 关键理解：

• 一条边 (u, v) 被存为一个结点
• 它通过 ilink 接入 u 的边链表
• 同时通过 jlink 接入 v 的边链表
• 因此，删除一条边只需修改两个指针，而不用像邻接表那样删两次

🔹 顶点结点（Vertex Node）------每个顶点一个

域名	含义
data	存储顶点的数据（如名称、编号）
firstedge	指向第一条与该顶点相连的边（即该顶点的边链表头指针）

✅ 举例：顶点 A

• firstedge 指向任意一条包含 A 的边（如 A---B）
• 通过该边的 ilink 或 jlink（取决于 A 是 ivex 还是 jvex），可继续找到 A 的其他邻边

🔹 示例图

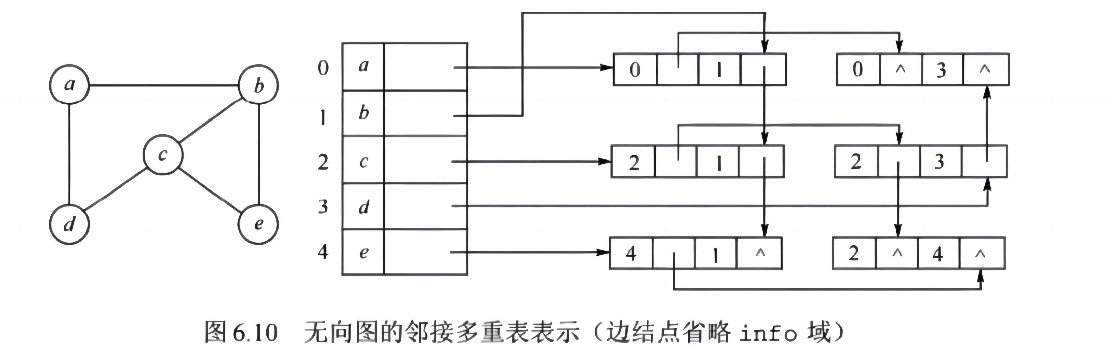
⚠️ 注：仅适用于无向图，考研较少考

---

✅ 存储方式对比表

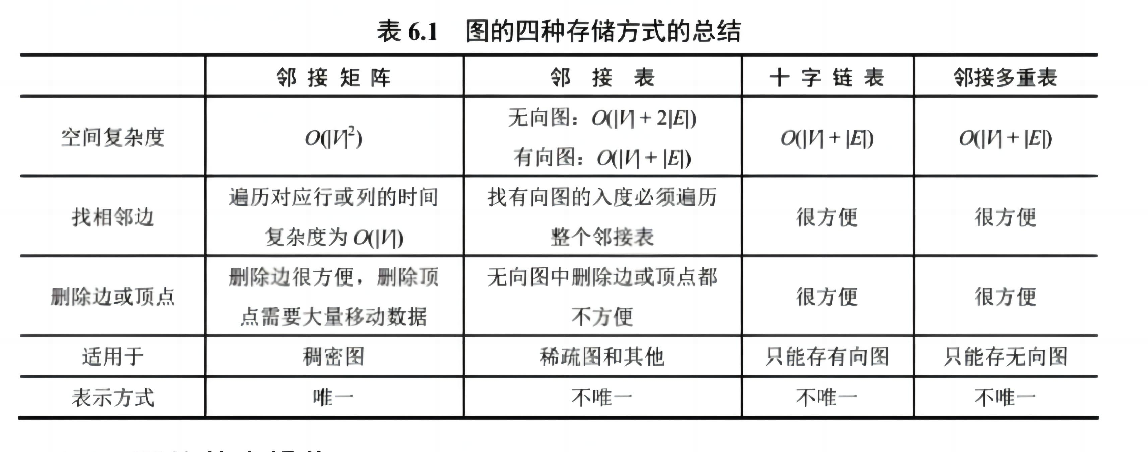
✅ 考研重点：邻接矩阵 vs 邻接表 的优缺点对比（必考选择题）

---

三、图的遍历（核心考点）

图的遍历是后续算法的基础，必须掌握！

1. 深度优先遍历（DFS）

• 类似树的前序遍历，使用栈 或递归实现
• 从某个顶点出发，尽可能深地访问子节点

✅ 特点：

• 可用于求解连通分量、拓扑排序、判断环

📌 算法步骤：

1. 标记当前顶点已访问
2. 依次访问其未访问的邻接顶点（递归）
3. 回溯

💡 考点：手写 DFS 序列、判断是否连通

---

2. 广度优先遍历（BFS）

• 使用队列，逐层扩展
• 从起点开始，先访问距离为 1 的顶点，再访问距离为 2 的......

✅ 特点：

• 可用于求最短路径（无权图）、层次遍历

📌 算法步骤：

1. 将起点入队
2. 出队一个顶点，访问其所有未访问邻接顶点并入队
3. 重复直到队空

💡 考点：手写 BFS 序列、求最短路径（无权图）

---

✅ DFS vs BFS 对比

项目	DFS	BFS
数据结构	栈 / 递归	队列
是否保证最短路径	否	是（无权图）
时间复杂度	O(n+e)	O(n+e)
空间复杂度	O(n)	O(n)
适用场景	连通性、环检测	最短路径、层次遍历

✅ 考研重点：会手写 DFS/BFS 遍历序列（给图后填空）

---

四、图的相关应用（重中之重！）

1. 最小生成树（MST）

在连通无向图中，选出 n-1 条边，使所有顶点连通且总权重最小。

✅ 两种经典算法：

算法	思想	时间复杂度
Prim 算法	从一个顶点开始，逐步加入最近的顶点	O(n^2) 或 O(elog⁡2n)
Kruskal 算法	按边权从小到大选边，避免成环	O(elog⁡2e)

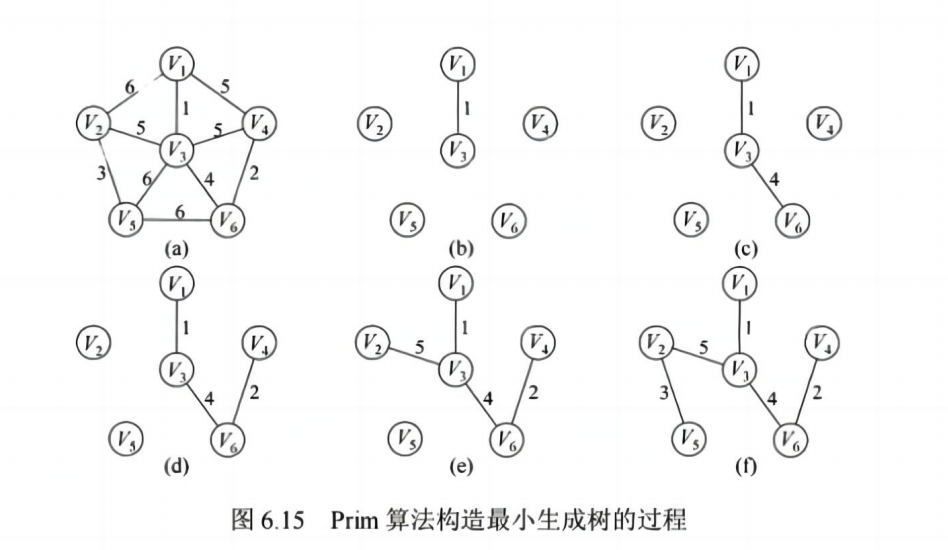
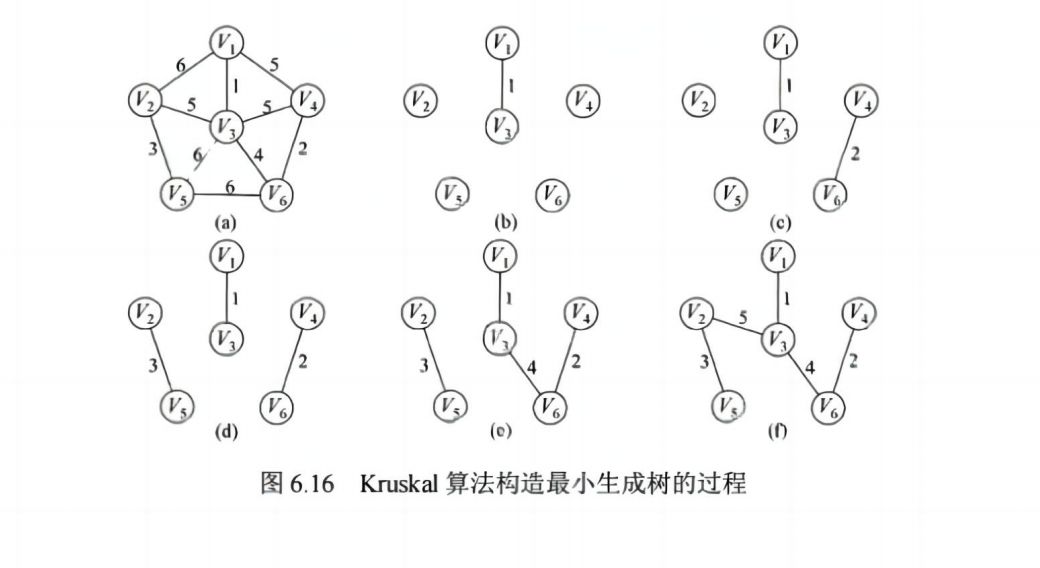
📌 区别：

• Prim：适合稠密图（顶点多）
• Kruskal：适合稀疏图（边少）
  💡 考点：比较两者的区别、手写 Prim/Kruskal 步骤

---

2. 最短路径

✅ Dijkstra 算法（单源最短路径）

• 从起点出发，每次选择距离最小的未访问顶点
• 适用于非负权图

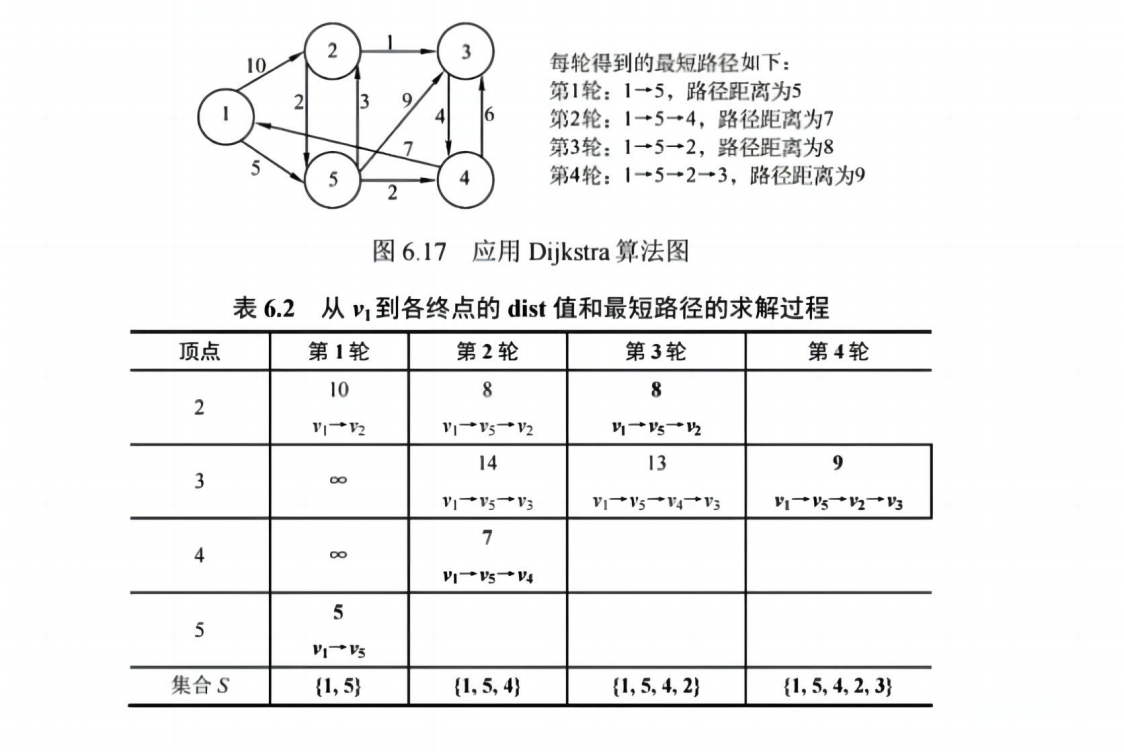
⚠️ 不适用于负权边！

✅ Floyd 算法（多源最短路径）

• 动态规划思想，枚举中间点
• 求任意两点间最短路径

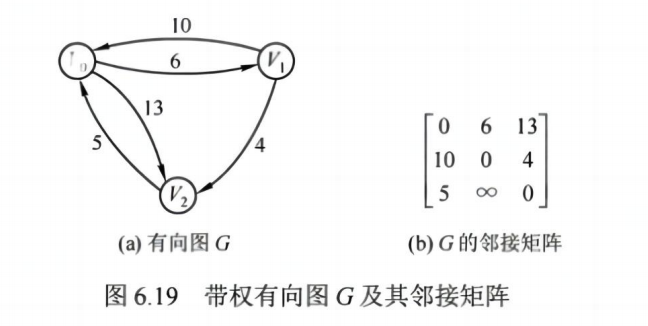
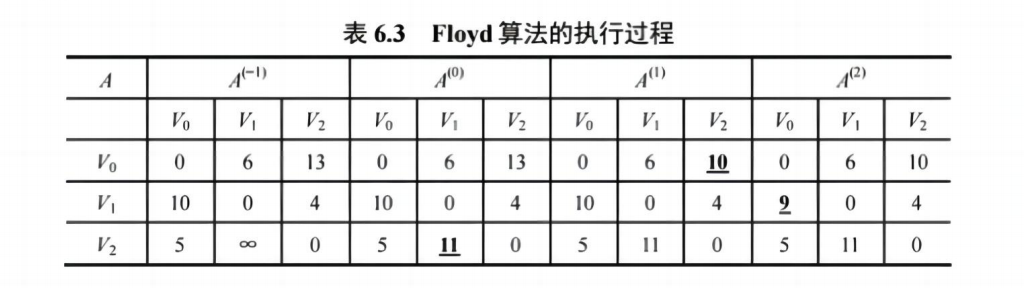
✅ 时间复杂度： O(n^3)，适合小规模图

✅ 最短路径算法对比表

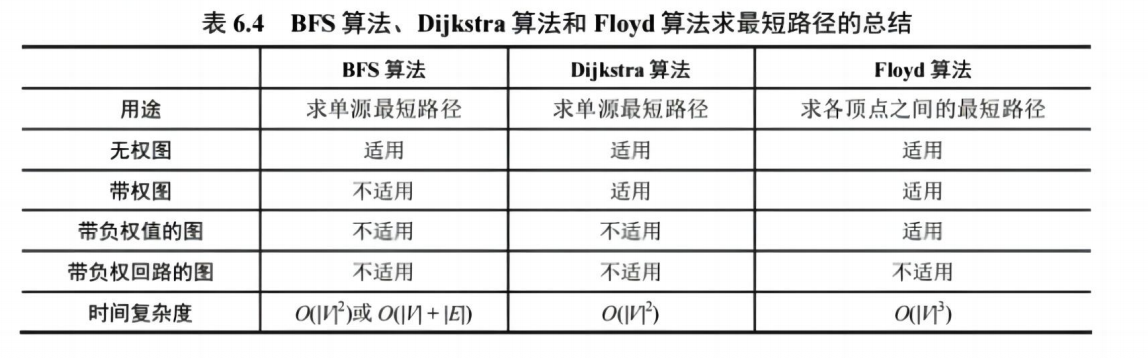
💡 考点：Dijkstra 与 Floyd 的应用场景对比、手写 Dijkstra 步骤

3. 拓扑排序（AOV 网）

AOV 网（Activity On Vertex）：顶点表示活动，边表示依赖关系

✅ 拓扑排序规则：

1. 找入度为 0 的顶点
2. 删除该顶点及其出边
3. 重复直到无顶点可删

✅ 排序过程

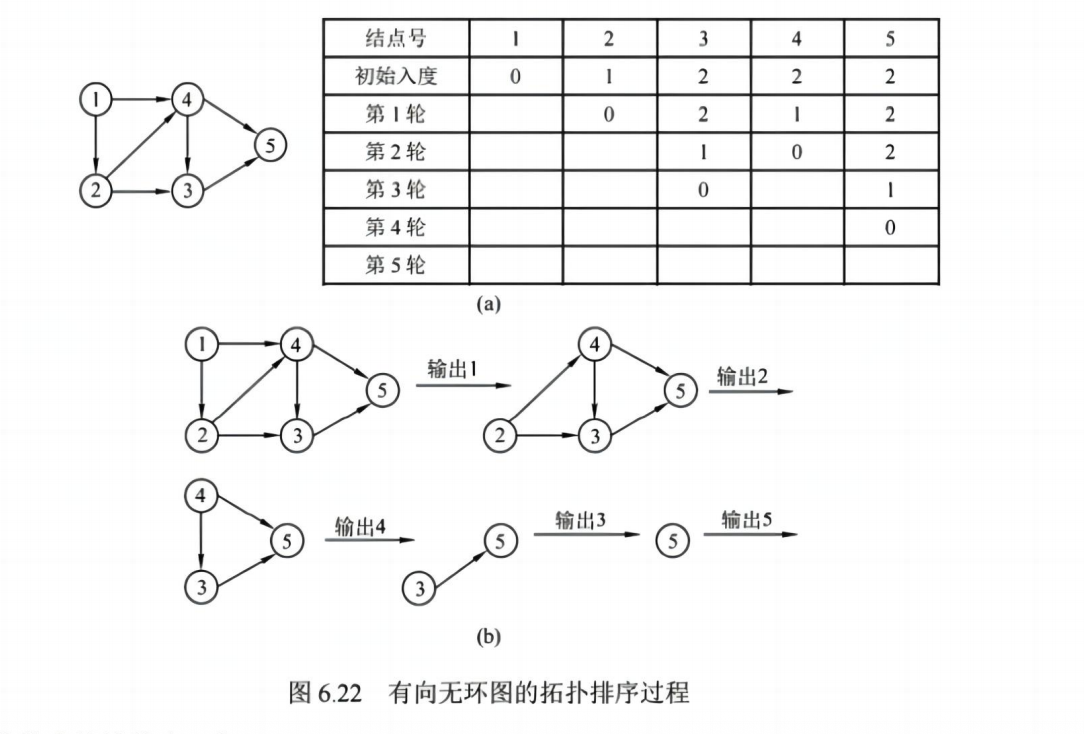
✅ 应用：

• 课程安排、任务调度

💡 考点：判断是否有环、手写拓扑序列

---

4. 关键路径（AOE 网）

AOE 网（Activity On Edge）：边表示活动，顶点表示事件

✅ 核心概念：

• 关键路径：从起点到终点的最长路径
• 关键活动：在关键路径上的活动
• 最早发生时间（ve）：顶点最早能发生的时刻
• 最迟发生时间（vl）：顶点最晚不能超过的时刻

✅ 求解步骤：

1. 求 ve（正向 DP）
2. 求 vl（反向 DP）
3. 求每个活动的最早开始时间（e）和最迟开始时间（l）
4. 若 e == l，则为关键活动

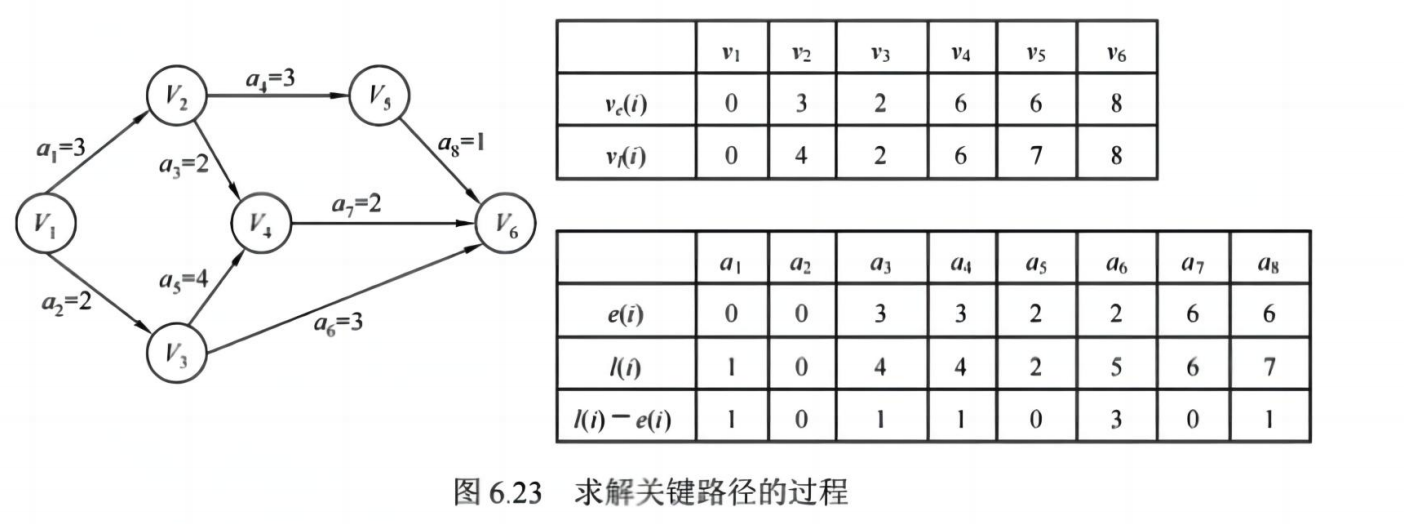
💡 考点：求关键路径、判断关键活动

---

五、高频考点总结

题型	考点
选择题	- 图的存储方式对比 - DFS/BFS 的特点 - MST 算法适用场景
填空题	- 写出 DFS/BFS 遍历序列 - 求最小生成树边数
简答题	- 解释 DFS 与 BFS 的区别 - 说明 Dijkstra 为何不能处理负权边
算法题	- 手写 Prim/Kruskal 步骤 - 实现拓扑排序 - 求关键路径

图相关算法时间复杂度对比

六、一句话口诀（背下来！）

"图存邻接表，遍历看 DFS/BFS；
最小生成树 用 Prim/Kruskal，最短路径 Dijkstra 和 Floyd；
拓扑排 AOV，关键路 AOE！"

---