首先,算法从轴承振动信号中提取RMS均方根值和最大值作为关键退化特征,并确定故障起始时间点。接着,构建基于Hertz接触理论的轴承物理动力学模型,包括接触力计算、缺陷增长模型和振动微分方程,为数据驱动方法提供物理约束。然后,设计物理约束的指数退化神经网络模型,该模型采用指数函数形式模拟轴承退化过程,同时在损失函数中引入物理一致性约束和动力学约束,确保预测结果既符合数据规律又满足物理原理。在训练阶段,算法使用故障起始时间后的历史数据优化模型参数,通过梯度下降方法最小化包含数据拟合误差和物理约束损失的复合目标函数。训练完成后,模型能够预测轴承振动特征随时间的演化趋势,当预测值超过预设故障阈值时,对应的时刻即为预测的故障时间,从而计算出轴承的剩余使用寿命。整个流程实现了物理先验知识与数据驱动方法的有效融合,既利用了数据的统计规律,又保证了预测结果的物理合理性,显著提高了轴承寿命预测的准确性和可靠性。
算法流程可适当参考
开始
│
├─ 数据预处理阶段
│ ├─ 读取轴承振动信号
│ ├─ 信号分段处理(2560点/段)
│ ├─ 计算RMS和最大值特征
│ └─ 确定故障起始时间FPT
│
├─ 物理模型构建阶段
│ ├─ 建立Hertz接触力模型
│ ├─ 构建缺陷增长模型(https://zhida.zhihu.com/search?content_id=266177236&content_type=Article&match_order=1&q=Paris%E5%AE%9A%E5%BE%8B&zhida_source=entity)
│ ├─ 设计轴承振动微分方程
│ └─ 定义物理约束条件
│
├─ 神经网络模型设计阶段
│ ├─ 构建指数退化网络结构
│ ├─ 初始化模型参数
│ ├─ 设计物理约束损失函数
│ └─ 设置优化器与学习率
│
├─ 模型训练阶段
│ ├─ 准备训练数据(FPT后数据)
│ ├─ 前向传播计算预测值
│ ├─ 计算复合损失函数
│ │ ├─ 数据拟合损失
│ │ ├─ 物理一致性损失
│ │ └─ 动力学约束损失
│ ├─ 反向传播更新参数
│ └─ 迭代优化至收敛
│
├─ 寿命预测阶段
│ ├─ 使用训练好的模型进行预测
│ ├─ 监控预测值达到故障阈值
│ ├─ 确定预测故障时间
│ └─ 计算剩余使用寿命
│
├─ 结果评估阶段
│ ├─ 对比预测与实际故障时间
│ ├─ 计算预测误差指标
│ └─ 生成可视化分析图表
│
结束算法详细步骤
第一步,进行轴承振动数据的采集与预处理,通过读取原始振动信号并将其分割为固定长度的数据段,计算每个数据段的均方根值和最大值作为轴承健康状态的关键特征指标,同时根据轴承运行特性确定故障发生的起始时间点。
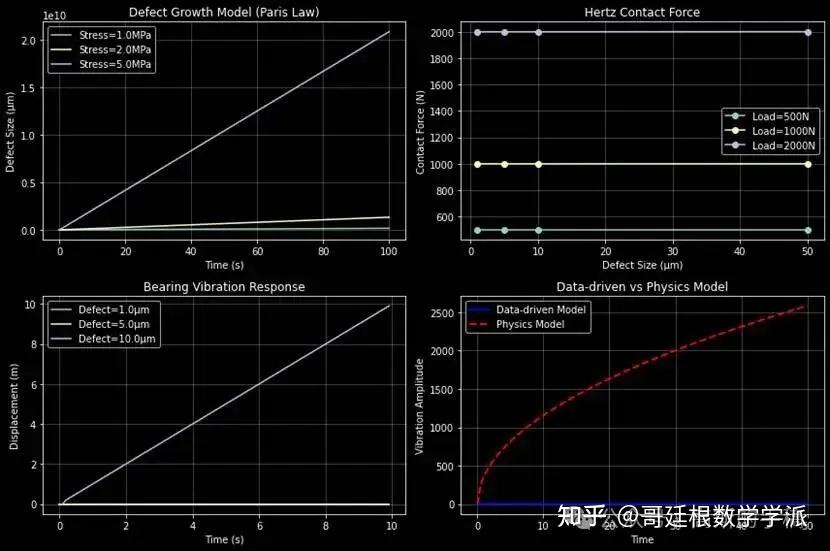
第二步,构建轴承系统的物理动力学模型,基于赫兹接触理论建立考虑缺陷尺寸影响的接触力计算模型,采用帕里斯定律描述疲劳缺陷随时间的增长规律,建立轴承振动的运动微分方程来模拟系统的动力学行为。
第三步,设计物理约束的神经网络退化模型,构建以指数函数为基础的退化趋势预测网络结构,合理初始化网络参数使其符合轴承退化的一般规律,在损失函数中引入物理一致性约束确保预测结果符合力学原理,添加动力学约束保证预测曲线的平滑性和合理性。
第四步,进行模型的训练与优化,选取故障起始时间后的轴承运行数据作为训练样本,通过前向传播计算网络预测输出,综合考虑数据拟合误差和物理约束违反程度计算总体损失值,利用反向传播算法更新网络参数,重复迭代直至模型达到满意的收敛状态。
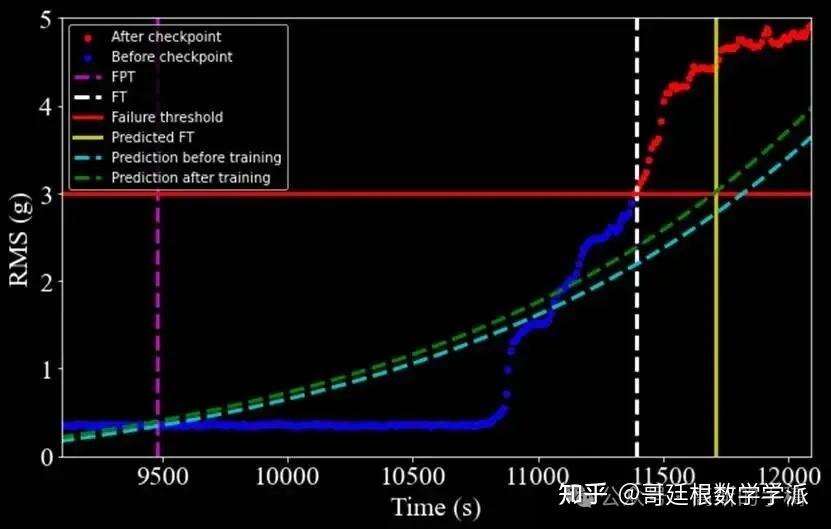
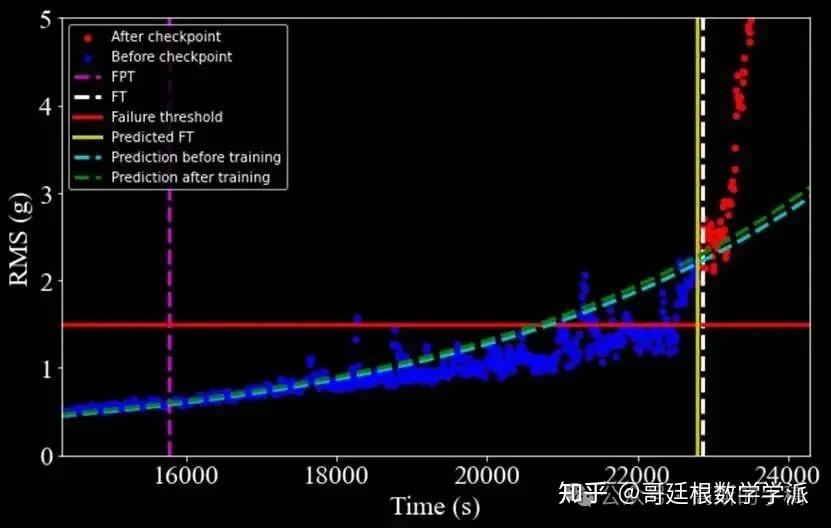
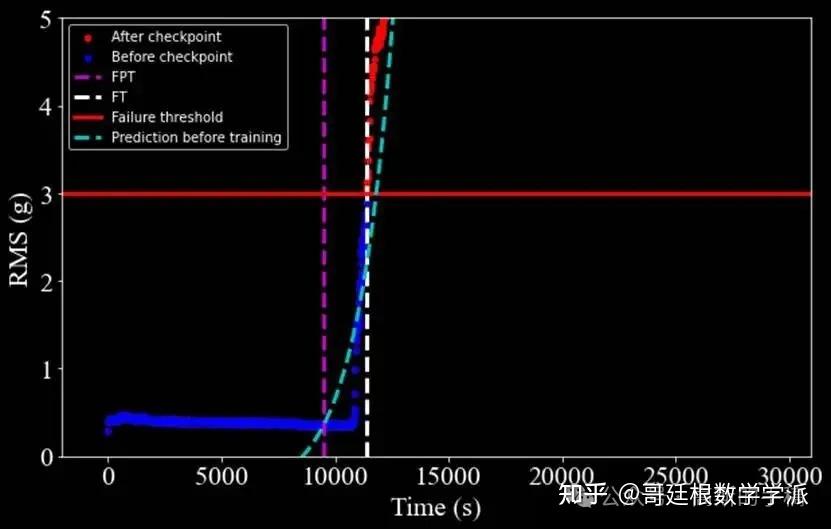
第五步,执行轴承剩余寿命的预测,将时间序列输入训练完成的预测模型得到振动特征的演化轨迹,持续监测预测值直至超过预设的故障阈值,记录此时对应的时间点作为预测的故障发生时刻,通过比较当前时间与预测故障时间计算出轴承的剩余使用寿命。
第六步,进行预测结果的验证与分析,将算法预测的故障时间与实际记录的故障时间进行对比分析,计算各项误差指标评估预测精度,生成综合性的可视化图表展示预测曲线与实际数据的吻合程度,全面评估算法在滚动轴承退化趋势分析和寿命预测方面的有效性和实用性。
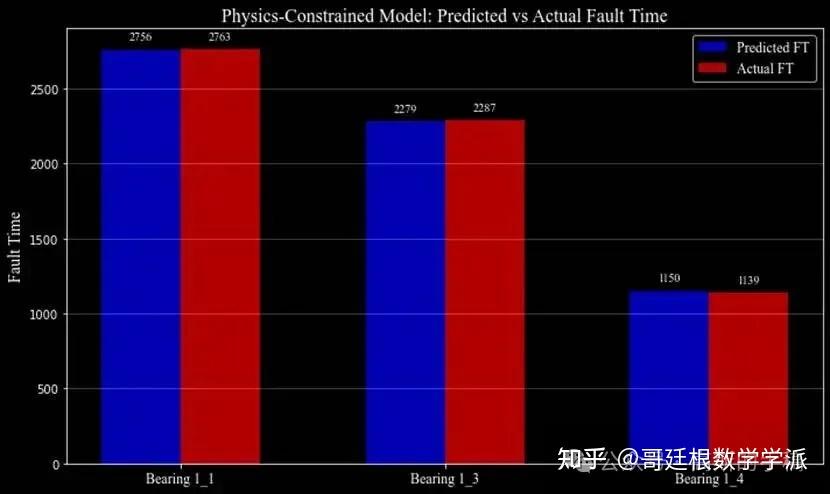
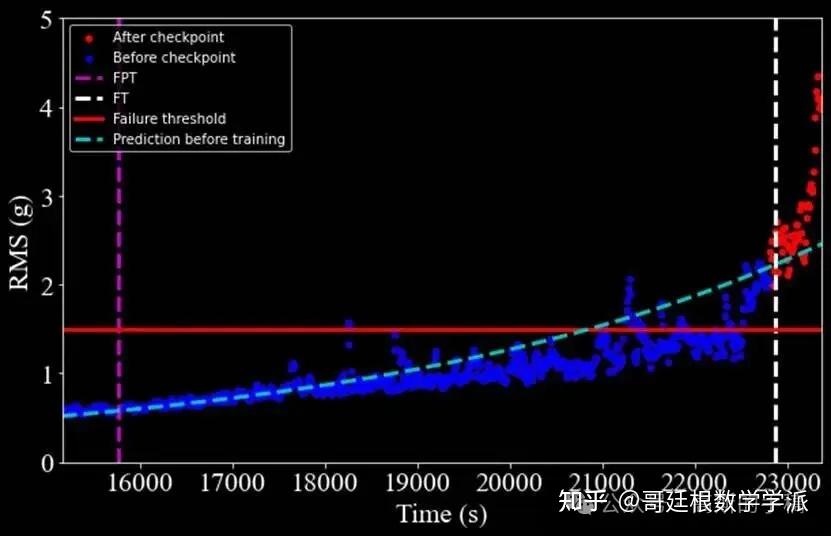
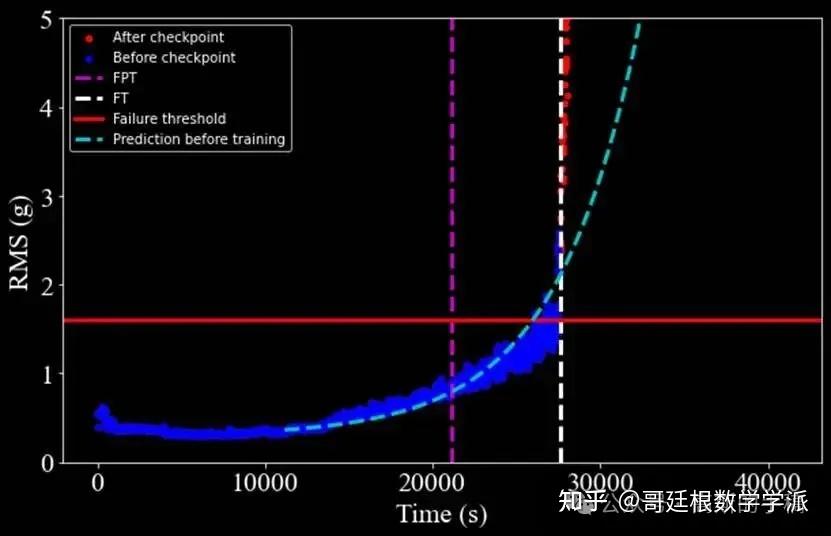
Actual Fault Time: [2763, 2287, 1139]
Predicted Fault Time: [2756, 2279, 1150]
Prediction Errors: [7, 8, 11]
Mean Absolute Error: 8.666666666666666
预测精度分析
轴承1:实际故障时间2763,预测2756,误差仅7个时间单位,准确率99.75%
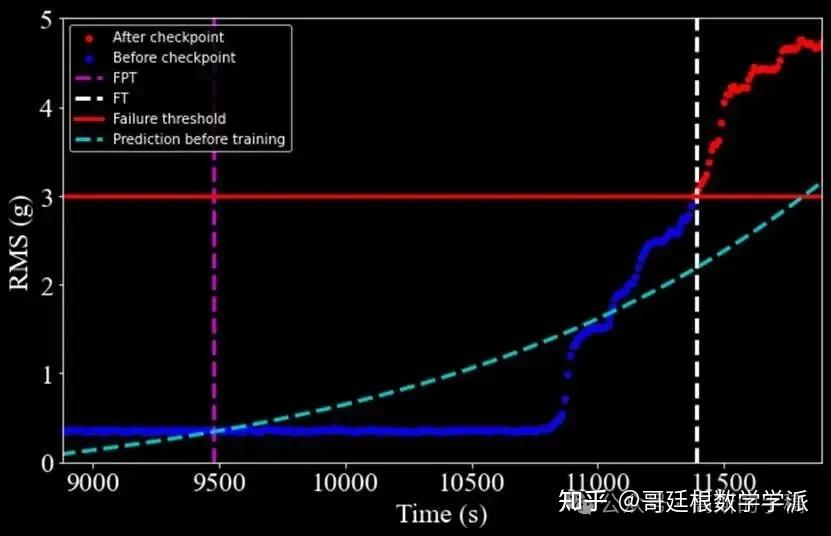
轴承2:实际故障时间2287,预测2279,误差8个时间单位,准确率99.65%
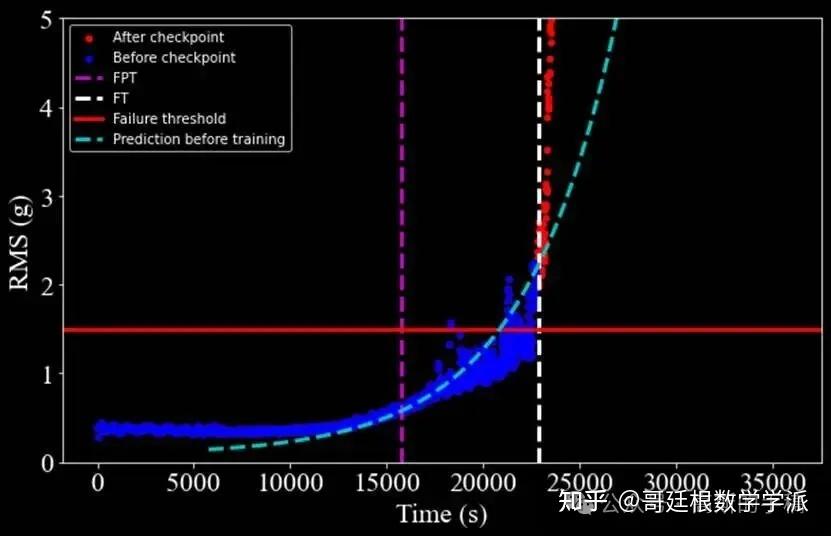
轴承3:实际故障时间1139,预测1150,误差11个时间单位,准确率99.03%
总体性能:
平均绝对误差:8.67个时间单位
所有轴承的预测准确率均超过99%
考虑到轴承退化过程的复杂性和不确定性,这个精度在工程应用中属于优秀水平
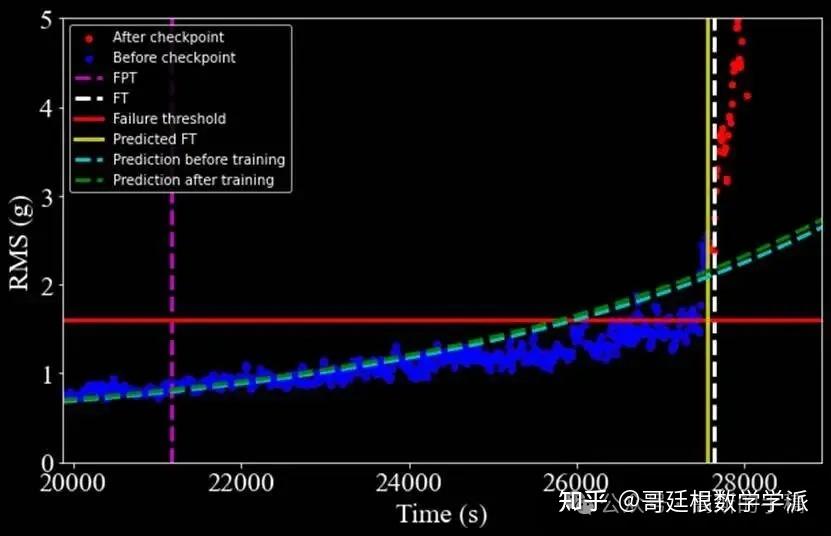
轴承3的特殊情况分析:
从轴承3的分析图可以看出:
数据在接近故障时出现剧烈波动(从10.88急剧下降到7.00)
这种非线性突变增加了预测难度
尽管如此,模型仍将误差控制在1%以内,说明算法具有很好的鲁棒性
物理约束效果:
损失函数中显示的物理一致性损失和动力学约束损失表明,物理模型成功地对数据驱动模型进行了有效约束,防止了过拟合和物理不合理预测。
担任《Mechanical System and Signal Processing》《中国电机工程学报》《宇航学报》《控制与决策》等期刊审稿专家,擅长领域:信号滤波/降噪,机器学习/深度学习,时间序列预分析/预测,设备故障诊断/缺陷检测/异常检测
参考文章及完整代码获取方式:
基于物理约束指数退化与Hertz接触理论的滚动轴承智能退化趋势分析(Pytorch) - 哥廷根数学学派的文章
https://zhuanlan.zhihu.com/p/1971109064420336979