自动驾驶雷达干扰缓解：探索主动策略论文精读

自动驾驶雷达干扰缓解：探索主动策略论文精读

C. Aydogdu et al., "Radar Interference Mitigation for Automated Driving: Exploring Proactive Strategies," in IEEE Signal Processing Magazine, vol. 37, no. 4, pp. 72-84, July 2020, doi: 10.1109/MSP.2020.2969319.

这篇文章的主线很清晰：车载FMCW雷达在密集交通环境中会互相"照射" ，而且这种干扰往往远强于目标回波；传统"事后补救"的抗干扰方法在车联网高度动态场景里可能不够用，于是作者系统分析了干扰机理与概率，并提出三类更偏"事前设计/协同"的主动策略：准正交FMCW波形、基于低速通信的资源协调、以及RadCom/OFDM体制。

---

1. 问题图景：为什么车载雷达干扰会变成"硬问题"

文章开头强调一个现实趋势：ADAS/自动驾驶普及带来路网中雷达收发机数量激增，且大多无协同地发射 ，干扰事件将显著增加。作者明确本文聚焦FMCW（最常见、最鲁棒的车载雷达），并将干扰影响量化为概率、严重度、以及对检测/跟踪的具体后果（虚警、漏检、鬼影目标等）。

下面这张图给出了"互相照射"场景：多车同频段雷达工作，某车的回波链路是"两程"衰落，而别车的直达干扰是"一程"传播，天然就更强。

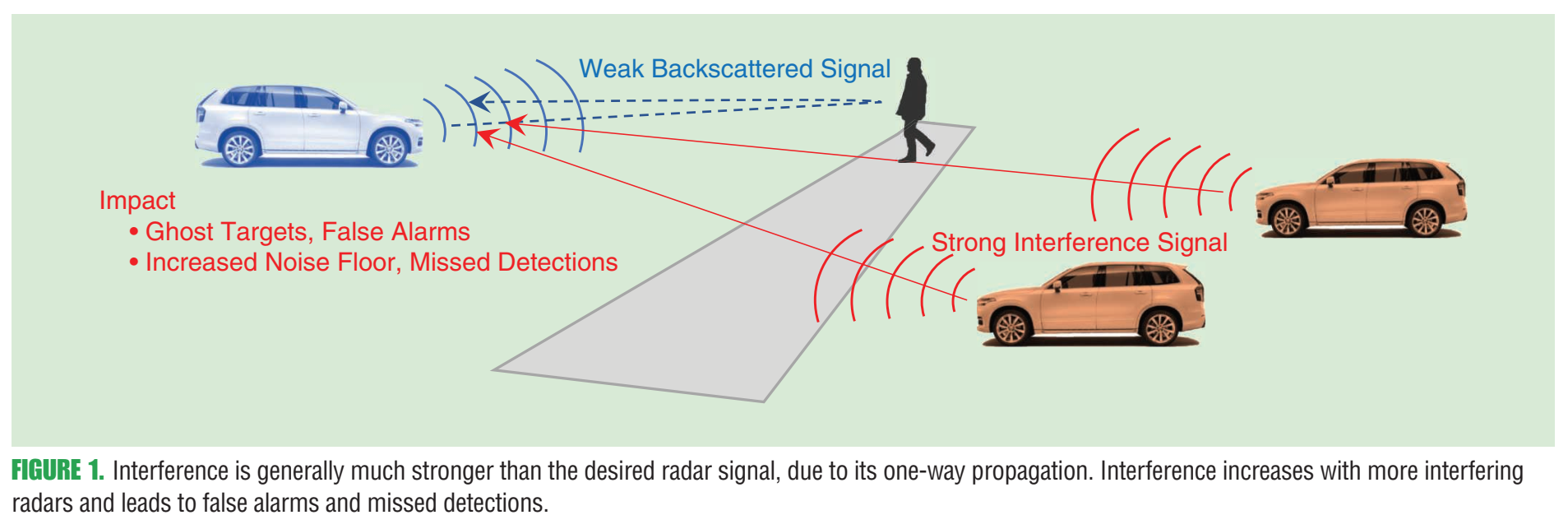
图1内容：多车雷达同时工作导致互扰；干扰路径多为雷达到雷达的直达链路（单程），而目标回波是雷达→目标→雷达（双程）。原文图注强调这是"radar interference problem illustration"。

---

2. FMCW体制与信号处理链：从发射到"距离-速度图"

文章用标准的K个线性调频chirp（sweep）描述FMCW发射信号。一个帧内K个chirp连续发射（此处作者假设无chirp间空闲，但也指出引入随机空闲可降低互扰概率）。

2.1 发射信号模型（式(1)(2)）

帧信号写成

s(t)=∑k=0K−1x(t−kT), s(t)=\sum_{k=0}^{K-1}x(t-kT), s(t)=k=0∑K−1x(t−kT),

其中单个chirp

x(t)=ej2π(fct+a2t2) rectT(t),a=BT. x(t)=e^{j2\pi\left(f_c t+\frac{a}{2}t^2\right)}\,\mathrm{rect}_T(t), \quad a=\frac{B}{T}. x(t)=ej2π(fct+2at2)rectT(t),a=TB.

这里 BBB 为扫频带宽、TTT 为chirp时长、fcf_cfc 为载频、aaa 为chirp斜率。

2.2 回波模型与"停-走假设"（式(3)）

假设单个点目标，复信道增益 ccc（包含路径损耗、天线增益、RCS等）、往返传播时延

τ=2Rc0, \tau=\frac{2R}{c_0}, τ=c02R,

归一化多普勒

ω=2vc0, \omega=\frac{2v}{c_0}, ω=c02v,

则在 stop-and-hop 假设下第 kkk 个chirp的接收信号形式为

rk(t)=c x(t+kT−τ)ej2πω(t+kT)+wk(t), r_k(t)=c\,x\left(t+kT-\tau\right)e^{j2\pi \omega (t+kT)}+w_k(t), rk(t)=cx(t+kT−τ)ej2πω(t+kT)+wk(t),

其中 0≤t≤T0\le t\le T0≤t≤T 是相对chirp起点的快时间，wk(t)w_k(t)wk(t) 为噪声。

2.3 图2：典型FMCW雷达收发链与处理流程（带"干扰插入点"）

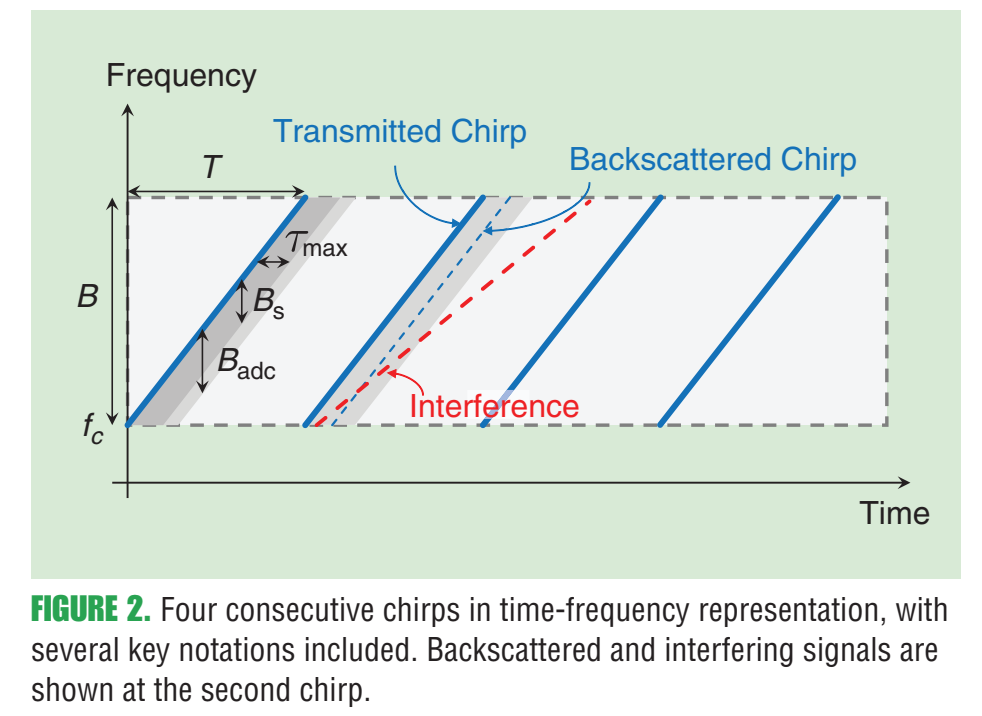
图2内容：从Tx基带→RF前端→接收端低噪放→混频"去chirp"(dechirp)→低通滤波→ADC→FFT/二维处理→检测/跟踪。图中还明确了干扰可能在混频后以"拍频/伪峰/噪底抬升"的方式进入后续处理链。原文图注为"FMCW radar signal processing chain"。

2.4 Stage 1：Dechirping 得到拍频信号（式(4)(5)）

接收信号与本振（本机发射）做共轭混频（dechirp），并忽略在一个CPI内相位总进动很小的项后，作者给出拍频（中频）信号近似为

yk(t)=c e−j2πaτ (t−τ/2) ej2πωkT ej2π(ω−aτ)t rectT(t−τ)+wk(t), y_k(t)=c\,e^{-j2\pi a\tau\,(t-\tau/2)}\,e^{j2\pi \omega kT}\,e^{j2\pi(\omega-a\tau)t}\, \mathrm{rect}_T(t-\tau)+w_k(t), yk(t)=ce−j2πaτ(t−τ/2)ej2πωkTej2π(ω−aτ)trectT(t−τ)+wk(t),

并对快时间采样 t=nTst=nT_st=nTs 得到

yk,n=yk(nTs)=c ej2π(ω−aτ)nTs ej2πωkT+wk,n. y_{k,n}=y_k(nT_s) =c\,e^{j2\pi(\omega-a\tau)nT_s}\,e^{j2\pi \omega kT}+w_{k,n}. yk,n=yk(nTs)=cej2π(ω−aτ)nTsej2πωkT+wk,n.

这两式揭示：拍频里"距离项 aτa\tauaτ"与"多普勒项 ω\omegaω"发生耦合（ω−aτ\omega-a\tauω−aτ），后面做二维匹配滤波/FFT时要处理这种range--Doppler coupling。

---

3. Delay--Doppler谱：二维匹配滤波（式(6)）与分辨率

Stage 2中，作者把 yk,ny_{k,n}yk,n 做二维指数匹配（可视作二维DFT/periodogram），定义某个时延-多普勒点 (τ^,ω^)(\hat\tau,\hat\omega)(τ^,ω^) 上的delay--Doppler响应为

z(τ^,ω^)=∑k=0K−1∑n=0Nmax⁡−1yk,n ej2πanTsτ^ e−j2πkTω^. z(\hat\tau,\hat\omega) =\sum_{k=0}^{K-1}\sum_{n=0}^{N_{\max}-1}y_{k,n}\, e^{j2\pi a nT_s \hat\tau}\,e^{-j2\pi kT\hat\omega}. z(τ^,ω^)=k=0∑K−1n=0∑Nmax−1yk,nej2πanTsτ^e−j2πkTω^.

该谱在真实目标附近产生峰值，常配合CFAR做检测；峰值与处理增益 Gp=KNmax⁡G_p=K N_{\max}Gp=KNmax 成正比。作者也指出其中的 fcωa\frac{f_c\omega}{a}afcω 是由FMCW固有的耦合引起的时延偏移，可在估计后补偿。

更关键的是，作者直接从式(6)给出FMCW的距离与速度分辨率（在 Nmax⁡N_{\max}Nmax 足够大时）

TR=c02B,Tv=λc2KT, T_R=\frac{c_0}{2B},\qquad T_v=\frac{\lambda_c}{2KT}, TR=2Bc0,Tv=2KTλc,

其中 λc\lambda_cλc 为载波波长。直观解释：带宽越大→距离分辨率越高；CPI越长（KTKTKT 越大）→速度分辨率越高。

---

4. 干扰为何"天然更强"：Friis vs Radar Equation（式(7)）

单链路下，作者用一个对比说明"为啥这事麻烦"：

目标回波受雷达方程（双程） 支配；而他车直达干扰受 Friis自由空间传播（单程） 支配，于是干扰功率远大于回波功率。

文中给出（符号按原文）回波与干扰功率的关系式（式(7)），核心结构是

Pint∝P Gtrx(4πr)2,Ptar∝P Gtrx2 σ(4π)3d4, P_{\text{int}}\propto \frac{P\,G_{\text{trx}}}{(4\pi r)^2},\qquad P_{\text{tar}}\propto \frac{P\,G_{\text{trx}}^2\,\sigma}{(4\pi)^3 d^4}, Pint∝(4πr)2PGtrx,Ptar∝(4π)3d4PGtrx2σ,

因此在 rrr 与 ddd 同量级且 σ\sigmaσ（RCS）取常见值时，通常 Pint≫PtarP_{\text{int}}\gg P_{\text{tar}}Pint≫Ptar。

这也解释了后文为何把干扰影响拆成两部分：一是"强度"（功率），二是"相干性"（是否会像目标一样形成尖锐峰/鬼影）。

---

5. 频谱现象：chirp斜率失配、相位噪声与"鬼影/噪底抬升"

5.1 图3：chirp斜率失配导致干扰能量在距离谱里"铺开/挤压"

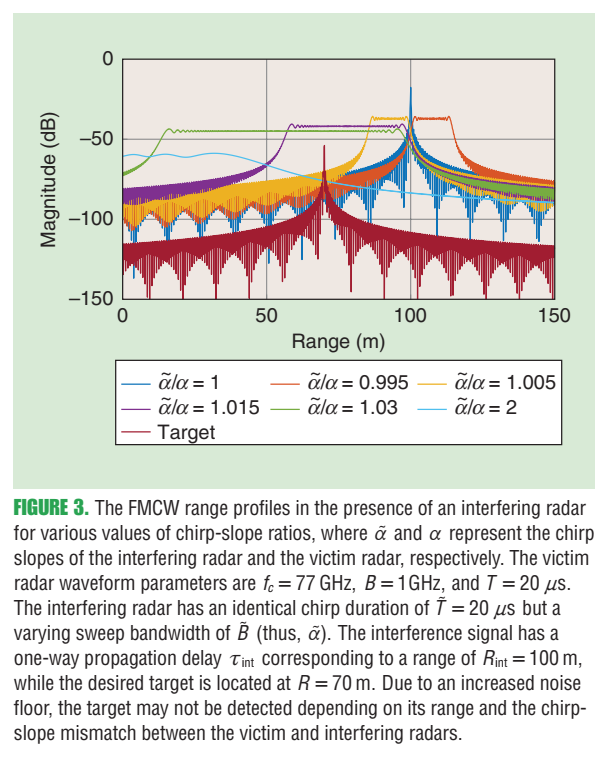
图3内容 ：受害雷达的距离谱在存在干扰雷达时，随斜率比 a~/a\tilde a/aa~/a 改变而出现明显差异：当斜率匹配程度不同，干扰在距离轴上的"形态"不同，可能形成局部峰值、也可能把噪底整体抬高，从而掩盖弱目标或引入虚假峰。原文说明参数如 fc=77f_c=77fc=77GHz、B=1B=1B=1GHz、T=20 μsT=20\,\mu sT=20μs 等，并强调干扰是单程传播而目标是双程传播。

5.2 图4：相位噪声造成谱展宽，细节丢失，弱目标更易被掩盖

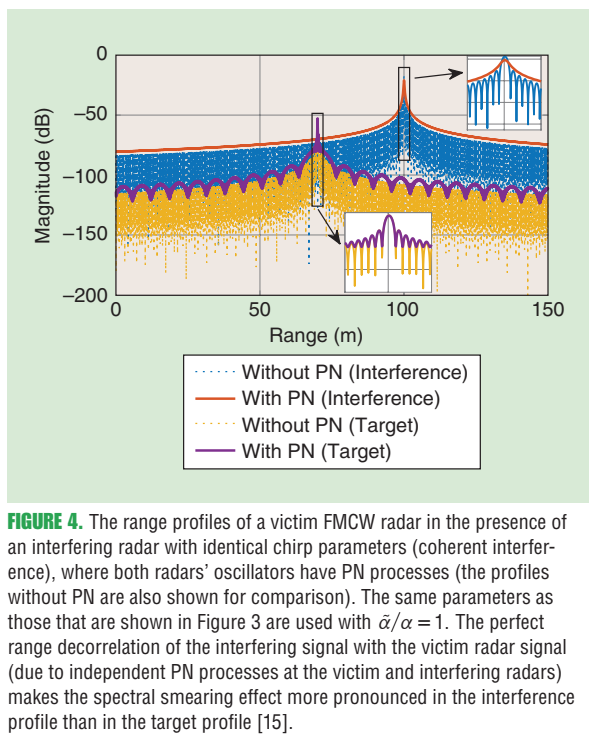
图4内容：考虑振荡器相位噪声（PN）后，无论目标回波还是干扰谱都会"涂抹/展宽"，但由于干扰更强，这种谱展宽会更显著地恶化检测性能，尤其会遮蔽弱目标。原文图注指出这里讨论"相干干扰"场景，并对比"有/无PN"两种情况。

---

6. 从单车到路网：随机几何下的网络干扰（图5、式(8)(9)）

作者把道路上车辆位置抽象为随机点过程，用随机几何分析平均干扰。关键设定是：在多车道高速路上，每条车道的车辆（或雷达）沿道路方向形成一维Poisson点过程 Φ(x)\Phi(x)Φ(x)，强度 1/Δ1/\Delta1/Δ（Δ\DeltaΔ 是平均车距）。

图5：六车道高速路的网络干扰示意

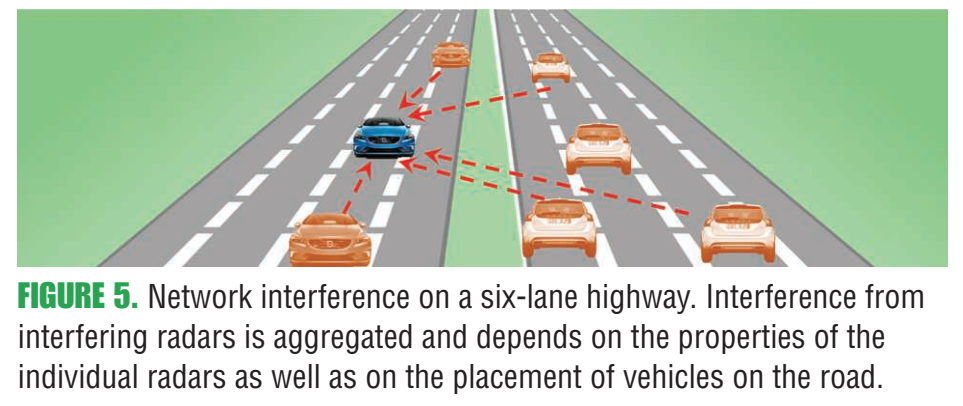
图5内容解读：受害车位于某条车道，周围多车道（对向、同向超车道等）车辆均可能形成干扰；作者将来自不同车道的干扰叠加，强调它与车辆空间分布、天线视场(FOV)等密切相关。

6.1 车道 ℓ\ellℓ 的聚合干扰（式(8)）

作者将某条车道 ℓ\ellℓ 上所有干扰车的贡献累加，写成（结构上是"点过程求和"）

Ip(ℓ)=∑x∈Φ(ℓ)P f Gtrx λ2(4π)2 r2(x), I_p(\ell)=\sum_{x\in \Phi(\ell)} P\,f\,\frac{G_{\text{trx}}\,\lambda^2}{(4\pi)^2\,r^2(x)}, Ip(ℓ)=x∈Φ(ℓ)∑Pf(4π)2r2(x)Gtrxλ2,

其中 r(x)r(x)r(x) 是从受害车到位置 xxx 的干扰车的距离，fff 是"发生干扰的概率/占空相关因子"（后面会精确解释），并且天线/FOV通过积分下限或增益项进入。

6.2 期望干扰（式(9)）的连续化积分形式

对Poisson点过程用平均化（本质上是Campbell定理），作者把干扰期望写成积分形式，并得到与 Δ\DeltaΔ（平均车距）成反比的趋势项。文中给出一个代表性化简结果（展示"车越密→干扰越大"的量化规律）：

E[Ip(ℓ)]=P Gtrxλ2(4π)2 fΔ ∫ϕℓ/2+∞1R2tan⁡2θ+x2 dx    ⇒    E[Ip(ℓ)]∝fΔ. \mathbb E[I_p(\ell)] = P\,\frac{G_{\text{trx}}\lambda^2}{(4\pi)^2}\,\frac{f}{\Delta}\, \int_{\phi_\ell/2}^{+\infty}\frac{1}{R^2\tan^2\theta+x^2}\,dx \;\;\Rightarrow\;\; \mathbb E[I_p(\ell)]\propto \frac{f}{\Delta}. E[Ip(ℓ)]=P(4π)2Gtrxλ2Δf∫ϕℓ/2+∞R2tan2θ+x21dx⇒E[Ip(ℓ)]∝Δf.

这里 RRR 是车道间距，ϕℓ\phi_\ellϕℓ 与FOV有关，积分下限体现"视场外不计入干扰"。

---

7. 图6：网络干扰如何抬升噪底并压垮SINR

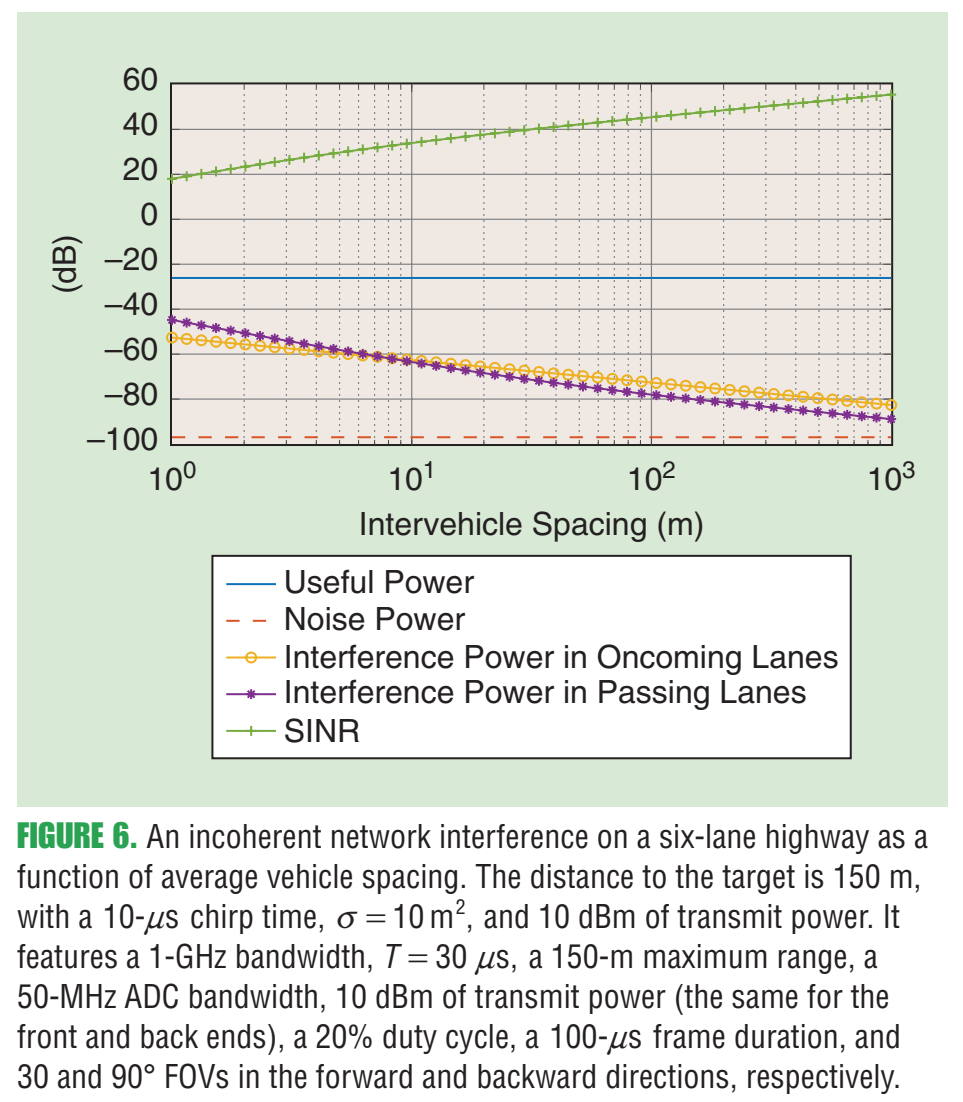
图6内容：横轴是平均车距（越小表示越拥挤），纵轴展示 useful power、noise power、来自对向车道/超车车道的干扰功率，以及合成后的SINR。随着车距减小，干扰项迅速上升，SINR大幅下降；作者还给出实验/仿真设定，例如目标距离150 m、带宽1 GHz、占空20%、不同FOV等。

这张图把"网络层面"的结论说得很直白：即便是非相干干扰，也能把噪底抬升"几十dB"量级，从而让弱目标（行人/自行车等低RCS）更难检测。

---

8. 把影响压成一个"可设计的指标"：SIR表达式（式(10)(11)）

作者用一种工程上非常好用的方式，把目标峰值（有用）与干扰功率写成

S=∣γ∣2Gp2,I≤f ∣γint∣2GpGI, S=|\gamma|^2 G_p^2,\qquad I\le f\,|\gamma_{\text{int}}|^2 G_p G_I, S=∣γ∣2Gp2,I≤f∣γint∣2GpGI,

其中 GIG_IGI 描述干扰与处理增益的耦合（相干程度不同，GIG_IGI 取值区间不同）。

进而得到SIR（式(11)）的分解形式：

$$

\mathrm{SIR}
\ge
\underbrace{\frac{|\gamma|^2 G_p}{f,|\gamma_{\text{int}}|^2 G_I}}_{\text{信道/几何+相干性}}

\underbrace{\frac{G_p}{f,G_I}}{\text{可设计}}
\cdot
\underbrace{\frac{G {\text{trx}},B}{(4\pi)^2,u,a,B_s}}{\text{波形/视场/ADC相关}}
\cdot
\underbrace{\frac{\sigma}{d^4}\cdot r^2} {\text{目标/几何}}

（原文把"不可控因素"和"可控因素"分开强调：第一因子多由场景决定，第二因子可通过占空比、chirp斜率、FOV、处理增益等优化，使SIR远大于1。） 这里已经埋下后文三种主动策略的逻辑：**降低 fff** 、降低有效斜率 aaa 或通过资源分离让"相干叠加"变得不可能，同时保持足够的距离/速度分辨率。 *** ** * ** *** ### 9. 主动策略一：准正交FMCW波形（图7、式(12)及其后推导） 作者从前面的分析得到一个干净的比例关系：干扰与 fu∝a xmax⁡ uB f_u \\propto \\frac{a\\,x_{\\max}\\,u}{B} fu∝Baxmaxu 相关（uuu 为占空比，xmax⁡x_{\\max}xmax 为最大往返时延），因此 **降低chirp斜率 a=B/Ta=B/Ta=B/T** （等价于延长chirp）能显著降低干扰。 #### 9.1 两个错位chirp的耦合（式(12)） 考虑一个chirp x(t)x(t)x(t) 与时间错位 TxT_xTx 的chirp x(t−Tx)x(t-T_x)x(t−Tx)（并以周期 TTT 重复），它们的功率泄漏/耦合（本质上是相关积分）： ρx(Tx)=∣1T∫0Tx(t) x∗(t−Tx) dt∣2≈∣sin⁡ ⁣(πBTTx2)πBTTx2∣2, \\rho_x(T_x)=\\left\|\\frac{1}{T}\\int_0\^T x(t)\\,x\^\*(t-T_x)\\,dt\\right\|\^2 \\approx \\left\|\\frac{\\sin\\!\\left(\\pi \\frac{B}{T}T_x\^2\\right)}{\\pi \\frac{B}{T}T_x\^2}\\right\|\^2, ρx(Tx)= T1∫0Tx(t)x∗(t−Tx)dt 2≈ πTBTx2sin(πTBTx2) 2, 并指出由于瞬时频差约为 BTTx\\frac{B}{T}T_xTBTx，所以这种耦合像"两正弦频差"的互相关一样迅速衰减，从而称这些波形为**准正交**。 #### 9.2 图7：单慢扫频(slow-sweep) FMCW实现"很多近似正交信号" 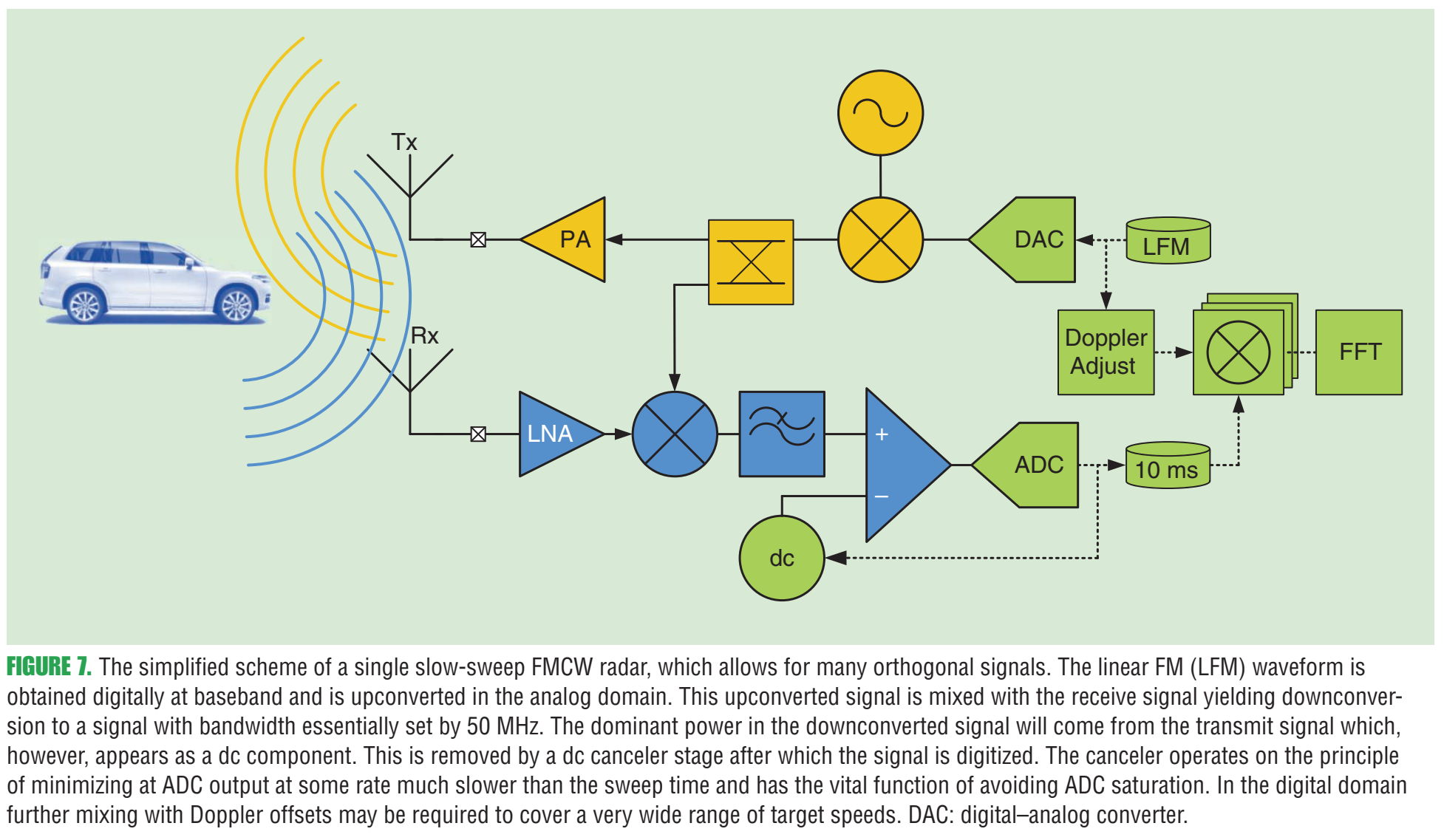 **图7内容**：这是一个"把慢扫频FMCW落地到硬件链路"的简化方案。LFM基带可数字生成，上变频后发射；接收端下变频得到基带后以约50 MHz带宽采样；强泄漏在数字域表现为直流分量，通过"dc消除/反馈抵消"而非极低截止频率的模拟高通来处理；同时允许在数字域做相位偏置（Doppler adjust）以改变不模糊速度范围。原文图注强调该方案"允许许多正交信号"，并解释了DAC/ADC/直流消除等关键模块。 #### 9.3 "长chirp"下的速度-距离解耦（式(13)(14)的意义） 作者指出式(5)里把速度当作简单多普勒近似会忽略小项，但在长chirp下必须保留，从而可在单chirp内解决range-speed ambiguity。文中写出更严格的形式（结构上是"相位含二次项的积分"）并用频域峰值与相位单调性做数值反演来求速度。 *** ** * ** *** ### 10. 主动策略二：借助低速通信做"频时资源协调"（图8、图9） 这部分作者把雷达当作"可被调度的发射机"，通过低速通信在车与车之间交换起始时间/频带等信息，使雷达在频时资源上尽量正交。文章提到可以用专用通信或蜂窝V2X，甚至把雷达与通信融合成RadCom单元。 #### 10.1 图8：RCU的频时共享与冲突消解机制 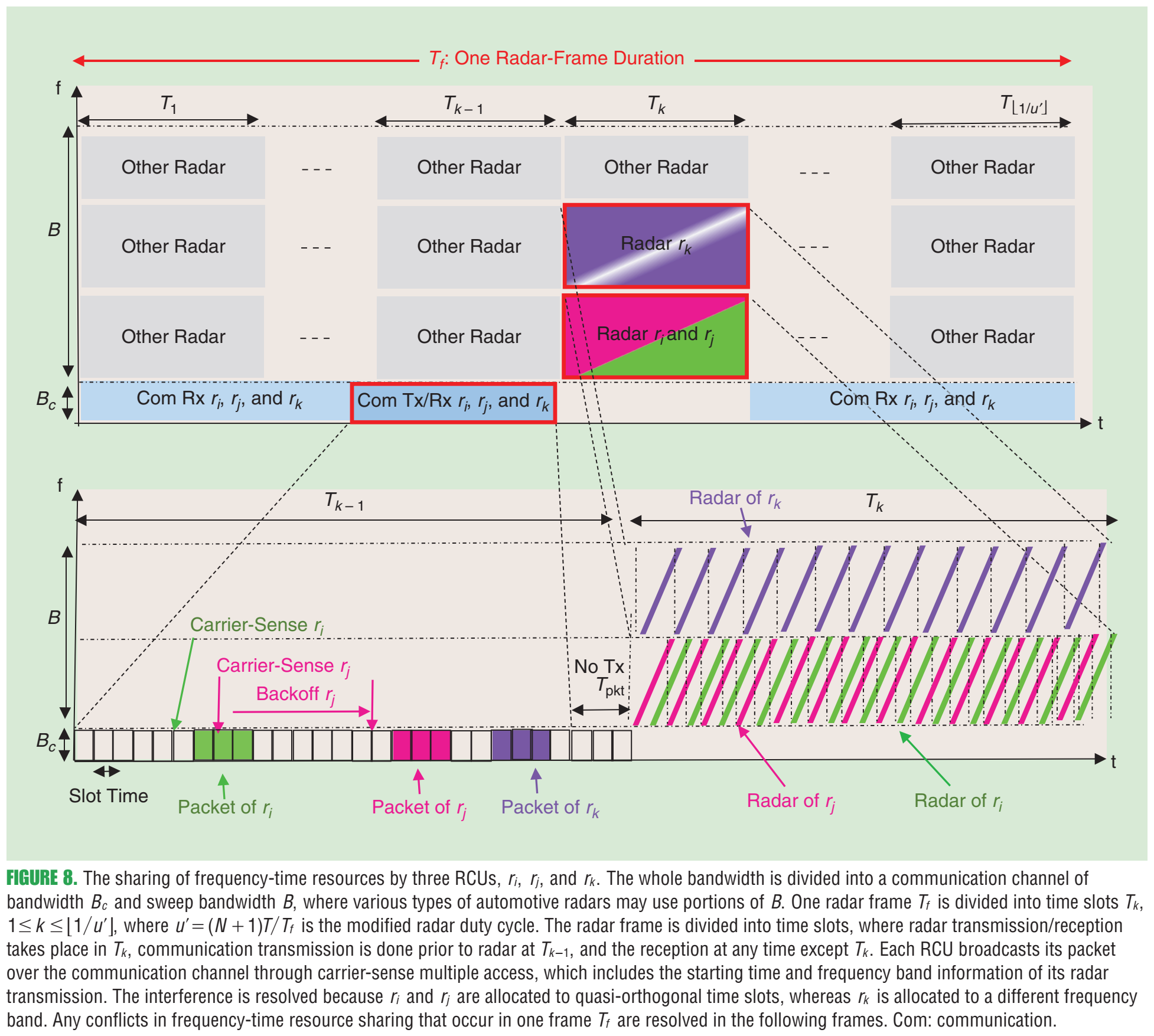 **图8内容解读** ：上半部分展示一个雷达帧 TfT_fTf 被切成时间槽，车载RCU在通信带宽 BcB_cBc 上广播自己的"雷达资源占用"，从而把不同车辆的雷达chirp安排到准正交的时间槽；若某车被分配到不同频带，则通过频分避免冲突。下半部分展示载波侦听/退避的通信过程与"下一帧再消解冲突"的思想。原文图注还解释了 ri,rj,rkr_i,r_j,r_kri,rj,rk 三个RCU：前两者用准正交时间槽，第三者换频带，且帧内冲突可在后续帧消解。 #### 10.2 图9：协调前后干扰概率 fff 的数量级差异 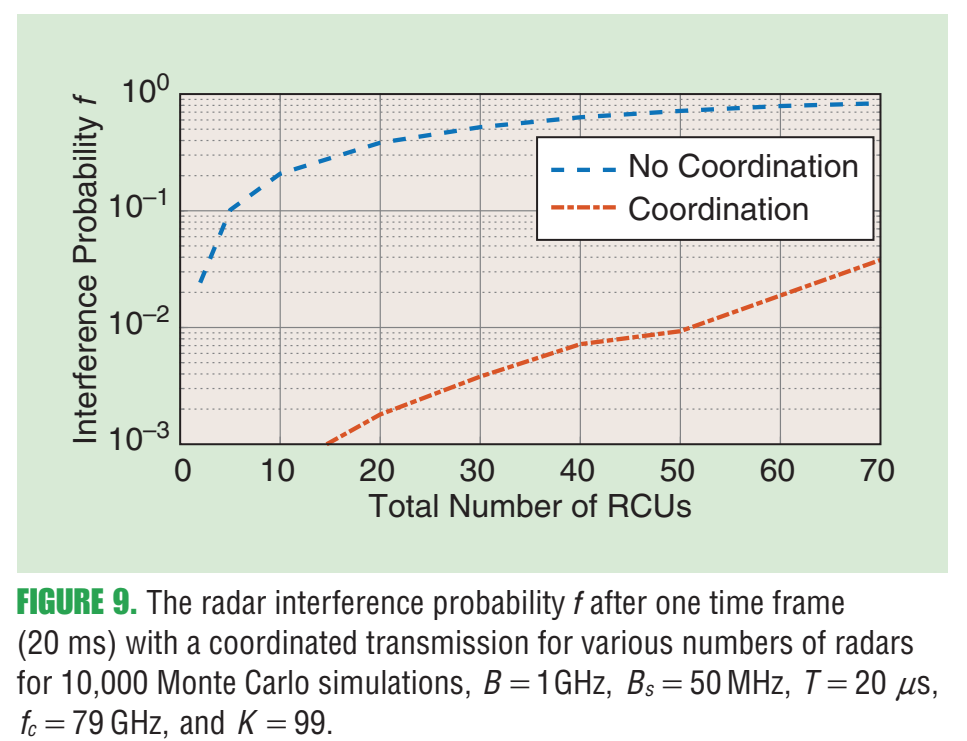 **图9内容解读** ：横轴为RCU（雷达/通信单元）数量，纵轴为干扰概率 fff（对Monte Carlo取期望意义）。图中"Coordination"曲线显著低于"No Coordination"，说明只要能在几十毫秒级做资源分配更新，干扰概率能大幅降低。原文图注给出仿真条件：一个帧20 ms、1 GHz带宽、Bs=50B_s=50Bs=50 MHz、T=20T=20T=20 ns、fc=79f_c=79fc=79 GHz、K=99K=99K=99、10,000次Monte Carlo等。 *** ** * ** *** ### 11. 主动策略三：RadCom / OFDM，尤其是"跳频的 stepped-frequency OFDM"（图10、式(15)、图11） 作者指出OFDM作为通信主力波形，天然适合做"雷达+通信"融合（RadCom）。难点在于常规OFDM雷达受ADC带宽限制，分辨率不如宽带FMCW；解决思路是用**stepped-frequency OFDM**：连续OFDM帧在不同载频上发射，拼接成更大的总带宽，同时每帧仍保持较小的基带带宽，从而降低ADC速率。 #### 11.1 图10：时间-频率资源协调示意（stepped vs narrow-band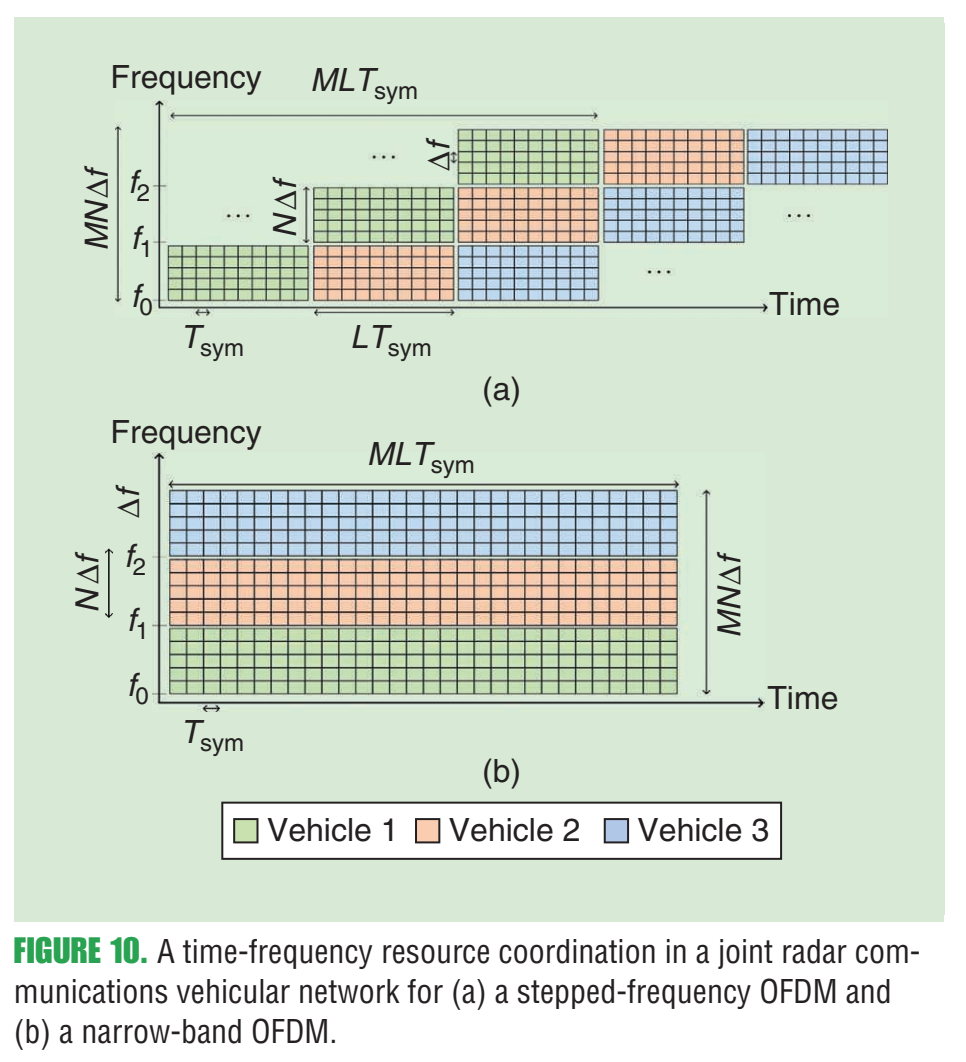）  **图10内容解读** ：图10(a)显示stepped-frequency OFDM：不同车辆被分配到互不重叠的时频块（不同载频/不同时间段），每个车辆通过跨M个载频帧的联合处理获得总带宽 MNΔfMN\\Delta fMNΔf 的高距离分辨率；图10(b)为窄带OFDM的资源分配。原文图注明确这是"time-frequency resource coordination in a joint radar communications vehicular network"。 #### 11.2 OFDM回波数据立方体模型（式(15)） 在"循环前缀长于时延、且小多普勒近似"等标准假设下，作者给出第 mmm 帧、第 ℓ\\ellℓ 个符号、第 nnn 个子载波上的接收符号模型 ##

y_{m,n,\ell}

c,x_{m,n,\ell},

e^{-j2\pi f_s n,\tau},

e^{j2\pi f_0, mL T_{\mathrm{sym}},\omega}

+w_{m,n,\ell},

其中 xm,n,ℓx_{m,n,\\ell}xm,n,ℓ 是发射数据/导频符号，wm,n,ℓw_{m,n,\\ell}wm,n,ℓ 为噪声。作者随后说明：对 (m,n)(m,n)(m,n) 维做匹配滤波可估计时延，对 (m,ℓ)(m,\\ell)(m,ℓ) 维处理可估计多普勒；跳频带来delay--Doppler耦合，可通过DFT实现里的相位校正项消除。 #### 11.3 图11：三种OFDM方案下"可容纳车辆数"的对比 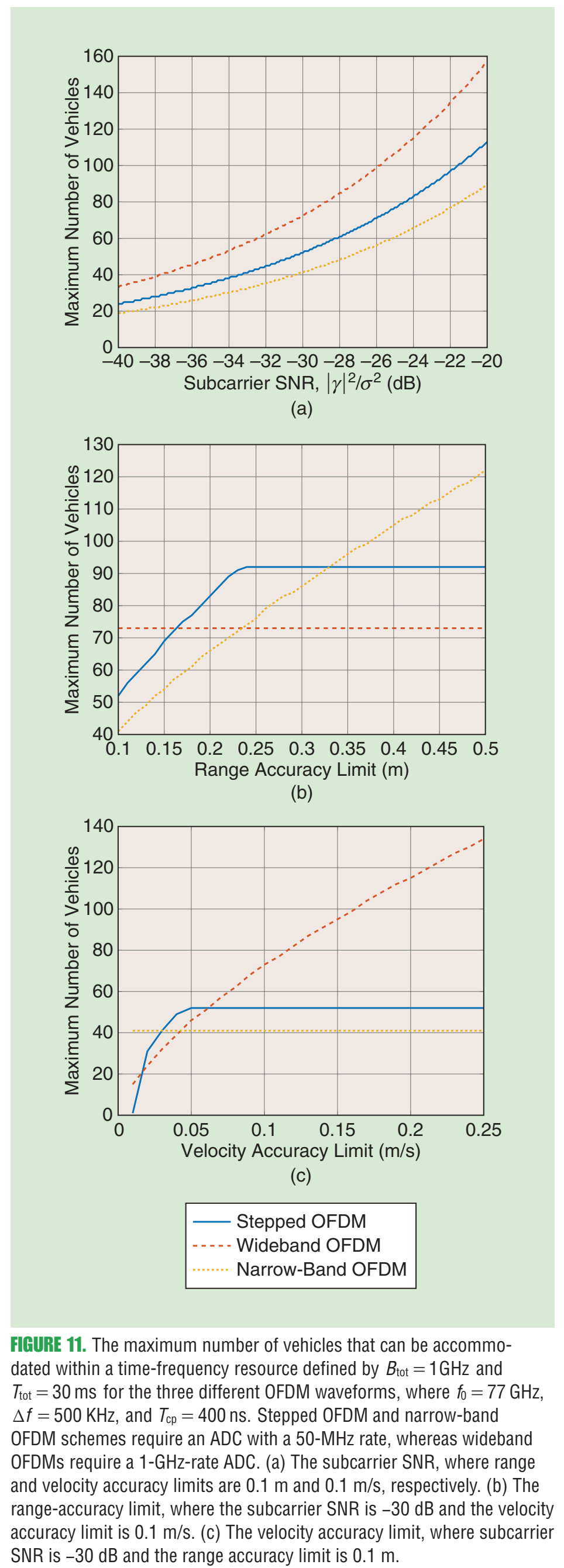 **图11内容** ：给定总资源 Btot=1B_{\\text{tot}}=1Btot=1 GHz 与 Ttot=30T_{\\text{tot}}=30Ttot=30 ms，比较 stepped-frequency、窄带、宽带OFDM三种方案可支持的车辆数；stepped-frequency在相同ADC（50 MHz）硬件约束下，通过"跳频换距离精度、牺牲部分多普勒精度"的灵活权衡，往往能塞进更多车辆。原文图注还说明宽带OFDM需要1 GHz采样率ADC，且(a)(b)©分别在不同精度/SNR约束下比较。 *** ** * ** *** ### 12. 图12：验证平台与实验环境 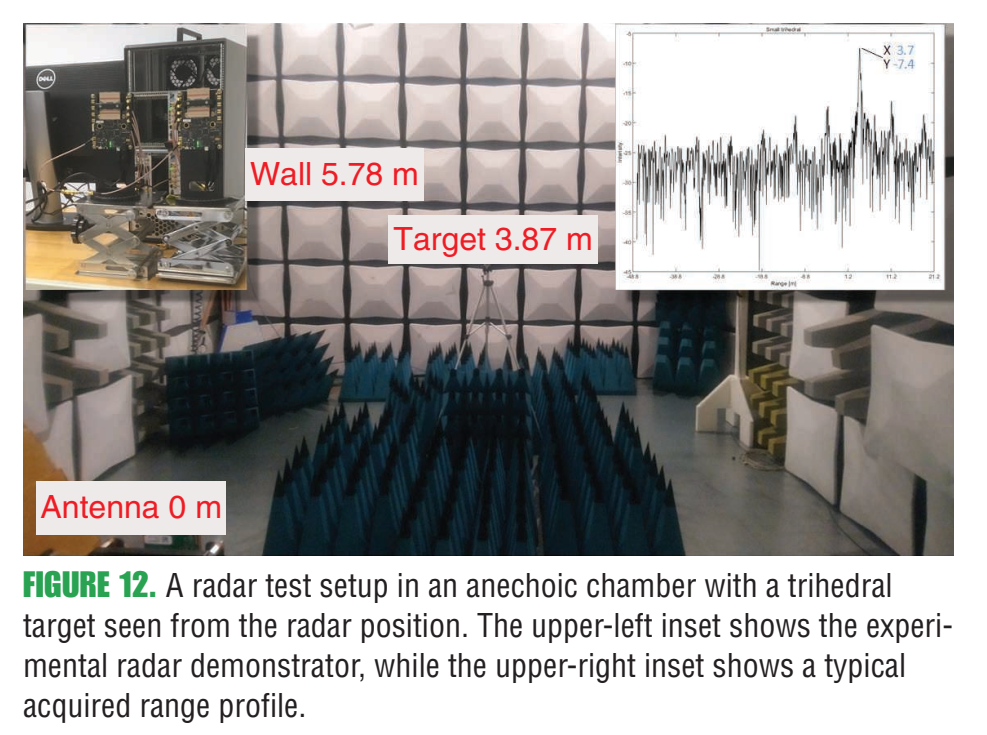 **图12内容** ：作者 **计划** 搭建包含毫米波前端、高速数字信号生成与采集、以及可控"独立干扰源"的演示平台，并在更真实环境里验证前文关于干扰概率、SINR、以及slow-ramp测速方法的理论分析。图中展示暗室(anechoic chamber)内的壁面与目标位置标注、以及典型距离谱插图。 *** ** * ** *** ## 附录：关键推导 ### A.1 从chirp模型推到拍频与"距离-速度耦合"（式(4)(5)的展开） 发射chirp： x(t)=ej2π(fct+a2t2)rectT(t). x(t)=e\^{j2\\pi(f_c t+\\frac{a}{2}t\^2)}\\mathrm{rect}_T(t). x(t)=ej2π(fct+2at2)rectT(t). 单目标回波（忽略幅度常数，保留时延与多普勒）可写成 rk(t)=c x(t−τ) ej2πω(t+kT)+wk(t). r_k(t)=c\\,x(t-\\tau)\\,e\^{j2\\pi \\omega (t+kT)}+w_k(t). rk(t)=cx(t−τ)ej2πω(t+kT)+wk(t). dechirp就是与本机chirp共轭相乘： yk(t)=rk(t) x∗(t)=c x(t−τ)x∗(t) ej2πω(t+kT)+wk(t)x∗(t). y_k(t)=r_k(t)\\,x\^\*(t) =c\\,x(t-\\tau)x\^\*(t)\\,e\^{j2\\pi \\omega (t+kT)}+w_k(t)x\^\*(t). yk(t)=rk(t)x∗(t)=cx(t−τ)x∗(t)ej2πω(t+kT)+wk(t)x∗(t). 把 x(t−τ)x∗(t)x(t-\\tau)x\^\*(t)x(t−τ)x∗(t) 的相位展开： x(t−τ)x∗(t)=exp⁡{j2π\[fc(t−τ)+a2(t−τ)2\]}exp⁡{−j2π\[fct+a2t2\]}=exp⁡{−j2πfcτ}exp⁡{j2πa2(t2−2tτ+τ2−t2)}=exp⁡{−j2πfcτ}exp⁡{−j2πatτ}exp⁡{j2πa2τ2}. \\begin{aligned} x(t-\\tau)x\^\*(t) \&=\\exp\\left\\{j2\\pi\\Big\[f_c(t-\\tau)+\\frac{a}{2}(t-\\tau)\^2\\Big\]\\right\\} \\exp\\left\\{-j2\\pi\\Big\[f_c t+\\frac{a}{2}t\^2\\Big\]\\right\\}\\\\ \&=\\exp\\left\\{-j2\\pi f_c\\tau\\right\\} \\exp\\left\\{j2\\pi\\frac{a}{2}\\big(t\^2-2t\\tau+\\tau\^2-t\^2\\big)\\right\\}\\\\ \&=\\exp\\left\\{-j2\\pi f_c\\tau\\right\\} \\exp\\left\\{-j2\\pi a t\\tau\\right\\} \\exp\\left\\{j2\\pi\\frac{a}{2}\\tau\^2\\right\\}. \\end{aligned} x(t−τ)x∗(t)=exp{j2π\[fc(t−τ)+2a(t−τ)2\]}exp{−j2π\[fct+2at2\]}=exp{−j2πfcτ}exp{j2π2a(t2−2tτ+τ2−t2)}=exp{−j2πfcτ}exp{−j2πatτ}exp{j2π2aτ2}. 把常数相位合并到 ccc 中（或写成 exp⁡{−j2πaτ(t−τ/2)}\\exp\\{-j2\\pi a\\tau(t-\\tau/2)\\}exp{−j2πaτ(t−τ/2)} 的形式），于是 yk(t)≈c e−j2πaτ(t−τ/2) ej2πω(t+kT)+wk(t), y_k(t)\\approx c\\,e\^{-j2\\pi a\\tau(t-\\tau/2)}\\,e\^{j2\\pi\\omega(t+kT)}+w_k(t), yk(t)≈ce−j2πaτ(t−τ/2)ej2πω(t+kT)+wk(t), 再把 exp⁡{j2πωt}\\exp\\{j2\\pi\\omega t\\}exp{j2πωt} 与 exp⁡{−j2πaτt}\\exp\\{-j2\\pi a\\tau t\\}exp{−j2πaτt} 合并，就得到原文式(4)的"拍频指数项"结构： yk(t)≈c ej2π(ω−aτ)t ej2πωkT⋅(窗口)+wk(t), y_k(t)\\approx c\\,e\^{j2\\pi(\\omega-a\\tau)t}\\,e\^{j2\\pi\\omega kT}\\cdot(\\text{窗口})+w_k(t), yk(t)≈cej2π(ω−aτ)tej2πωkT⋅(窗口)+wk(t), 对应采样 t=nTst=nT_st=nTs 直接得 yk,n=c ej2π(ω−aτ)nTs ej2πωkT+wk,n, y_{k,n}=c\\,e\^{j2\\pi(\\omega-a\\tau)nT_s}\\,e\^{j2\\pi\\omega kT}+w_{k,n}, yk,n=cej2π(ω−aτ)nTsej2πωkT+wk,n, 与原文式(4)(5)同型。 这里的关键点是：在单个chirp内，快时间频率项是 ω−aτ\\omega-a\\tauω−aτ，所以**距离与速度混在一起** ；必须通过跨chirp的慢时间维度（kkk 维）来把 ω\\omegaω 单独拉出来。 *** ** * ** *** ### A.2 从二维periodogram推分辨率：为什么 TR=c0/(2B)T_R=c_0/(2B)TR=c0/(2B)，Tv=λc/(2KT)T_v=\\lambda_c/(2KT)Tv=λc/(2KT) 式(6)本质是对二维复指数的匹配滤波/DFT： z(τ\^,ω\^)=∑k=0K−1∑n=0Nmax⁡−1yk,n ej2πanTsτ\^ e−j2πkTω\^.(原文式(6))    :contentReference\[oaicite:37\]index=37 z(\\hat\\tau,\\hat\\omega)= \\sum_{k=0}\^{K-1}\\sum_{n=0}\^{N_{\\max}-1} y_{k,n}\\,e\^{j2\\pi a nT_s \\hat\\tau}\\,e\^{-j2\\pi kT\\hat\\omega}. \\quad \\text{(原文式(6))} \\;\\; :contentReference\[oaicite:37\]{index=37} z(τ\^,ω\^)=k=0∑K−1n=0∑Nmax−1yk,nej2πanTsτ\^e−j2πkTω\^.(原文式(6)):contentReference\[oaicite:37\]index=37 把无噪单目标的 yk,n=c ej2π(ω−aτ)nTsej2πωkTy_{k,n}=c\\,e\^{j2\\pi(\\omega-a\\tau)nT_s}e\^{j2\\pi\\omega kT}yk,n=cej2π(ω−aτ)nTsej2πωkT 代入： z(τ\^,ω\^)=c∑k=0K−1ej2πωkTe−j2πkTω\^∑n=0Nmax⁡−1ej2π(ω−aτ)nTsej2πanTsτ\^=c\[∑k=0K−1ej2π(ω−ω\^)kT\]\[∑n=0Nmax⁡−1ej2π(ω−aτ+aτ\^)nTs\]. \\begin{aligned} z(\\hat\\tau,\\hat\\omega) \&=c\\sum_{k=0}\^{K-1}e\^{j2\\pi\\omega kT}e\^{-j2\\pi kT\\hat\\omega} \\sum_{n=0}\^{N_{\\max}-1}e\^{j2\\pi(\\omega-a\\tau)nT_s}e\^{j2\\pi a nT_s\\hat\\tau}\\\\ \&=c\\left\[\\sum_{k=0}\^{K-1}e\^{j2\\pi(\\omega-\\hat\\omega)kT}\\right\] \\left\[\\sum_{n=0}\^{N_{\\max}-1}e\^{j2\\pi(\\omega-a\\tau+a\\hat\\tau)nT_s}\\right\]. \\end{aligned} z(τ\^,ω\^)=ck=0∑K−1ej2πωkTe−j2πkTω\^n=0∑Nmax−1ej2π(ω−aτ)nTsej2πanTsτ\^=c\[k=0∑K−1ej2π(ω−ω\^)kT\]\[n=0∑Nmax−1ej2π(ω−aτ+aτ\^)nTs\]. 两项都是有限长度几何级数，其幅度包络是Dirichlet核；主瓣零点间隔由指数"频率"的分辨力决定。 * **距离（时延）分辨率** 来自第二项对 τ\^\\hat\\tauτ\^ 的敏感度。令 ντ≜(ω−aτ+aτ\^). \\nu_\\tau \\triangleq (\\omega-a\\tau+a\\hat\\tau). ντ≜(ω−aτ+aτ\^). 当 ω\^\\hat\\omegaω\^ 已靠近 ω\\omegaω（或把耦合补偿后），主瓣主要由 a(τ\^−τ)a(\\hat\\tau-\\tau)a(τ\^−τ) 决定。第二项主瓣宽度满足 a(τ\^−τ)Ts≈1Nmax⁡⇒Δτ≈1aNmax⁡Ts. a(\\hat\\tau-\\tau)T_s \\approx \\frac{1}{N_{\\max}}\\quad\\Rightarrow\\quad \\Delta\\tau \\approx \\frac{1}{a N_{\\max}T_s}. a(τ\^−τ)Ts≈Nmax1⇒Δτ≈aNmaxTs1. 又因为快时间观测长度 Nmax⁡Ts≈TN_{\\max}T_s\\approx TNmaxTs≈T，且 a=B/Ta=B/Ta=B/T，得 Δτ≈1(B/T) T=1B. \\Delta\\tau \\approx \\frac{1}{(B/T)\\,T}=\\frac{1}{B}. Δτ≈(B/T)T1=B1. 换成距离 R=c0τ/2R=c_0\\tau/2R=c0τ/2，于是 ΔR=c02Δτ≈c02B, \\Delta R=\\frac{c_0}{2}\\Delta\\tau\\approx \\frac{c_0}{2B}, ΔR=2c0Δτ≈2Bc0, 即原文给出的 TR=c0/(2B)T_R=c_0/(2B)TR=c0/(2B)。 * **速度（多普勒）分辨率** 来自第一项对 ω\^\\hat\\omegaω\^ 的敏感度。其主瓣宽度满足 (ω−ω\^)T≈1K⇒Δω≈1KT. (\\omega-\\hat\\omega)T \\approx \\frac{1}{K}\\quad\\Rightarrow\\quad \\Delta\\omega \\approx \\frac{1}{KT}. (ω−ω\^)T≈K1⇒Δω≈KT1. 将 ω=2v/c0\\omega=2v/c_0ω=2v/c0，得 Δv=c02Δω≈c02KT. \\Delta v=\\frac{c_0}{2}\\Delta\\omega\\approx \\frac{c_0}{2KT}. Δv=2c0Δω≈2KTc0. 原文写成 λc/(2KT)\\lambda_c/(2KT)λc/(2KT) 的等价形式，是因为在很多雷达教材里用 fD=2v/λcf_D=2v/\\lambda_cfD=2v/λc，两者只差"用 ω\\omegaω 还是用 fDf_DfD"的记号。 *** ** * ** *** ### A.3 "干扰概率因子" fff 的来源：为什么它会与占空比/ADC带宽/斜率相关（通向式(11)） 在FMCW里，干扰并非总是"全时全频"落在受害雷达的有效拍频带内。作者在式(11)前的推导把"会造成有效干扰的时间/频率重叠比例"压成一个概率因子 fff，并强调可通过设计减小它。 一个常见推导思路（与文中"干扰与 u,a,Bsu, a, B_su,a,Bs 等成比例"的结论一致）如下： dechirp后，来自干扰雷达的拍频会出现在受害雷达的低通+ADC带宽 BsB_sBs 内，条件近似可写成 ∣(ωint−aτint)−(ω−aτ)∣≤Bs/2. \|(\\omega_{\\text{int}}-a\\tau_{\\text{int}})-(\\omega-a\\tau)\| \\le B_s/2. ∣(ωint−aτint)−(ω−aτ)∣≤Bs/2. 当车辆位置/起始时间随机时，τint\\tau_{\\text{int}}τint 在 \[0,τmax⁡\]\[0,\\tau_{\\max}\]\[0,τmax\] 的有效范围内变化（τmax⁡=2Rmax⁡/c0\\tau_{\\max}=2R_{\\max}/c_0τmax=2Rmax/c0），而拍频随 τ\\tauτ 的变化率就是斜率 aaa。因此"落入带宽窗"的概率量级 f∼u⋅Bsaτmax⁡或等价地f∝uaτmax⁡B, f \\sim u\\cdot \\frac{B_s}{a\\tau_{\\max}} \\quad\\text{或等价地}\\quad f \\propto u\\frac{a\\tau_{\\max}}{B}, f∼u⋅aτmaxBs或等价地f∝uBaτmax, 具体系数与精确假设有关，但依赖关系与作者在准正交部分写的 fu∝a xmax⁡ uB f_u \\propto \\frac{a\\,x_{\\max}\\,u}{B} fu∝Baxmaxu 一致（这里 xmax⁡x_{\\max}xmax 对应最大往返时延）。 这也解释了三种主动策略分别在"降低有效斜率/延长chirp""降低重叠概率（调度）""把资源做成严格正交（OFDM时频分配）"三个方向发力。 *** ** * ** *** ### A.4 从点过程求和到积分期望：式(8)→式(9)的详细一步 式(8)是车道 ℓ\\ellℓ 上Poisson点过程 Φ(ℓ)\\Phi(\\ell)Φ(ℓ) 的求和形式。 为了求其期望，用Campbell定理： E\[∑x∈Φg(x)\]=λ∫Rg(x) dx, \\mathbb E\\left\[\\sum_{x\\in\\Phi} g(x)\\right\]=\\lambda\\int_{\\mathbb R} g(x)\\,dx, E\[x∈Φ∑g(x)\]=λ∫Rg(x)dx, 其中 λ=1/Δ\\lambda=1/\\Deltaλ=1/Δ。 把 g(x)=PfGtrxλ2(4π)2r2(x)g(x)=P f\\frac{G_{\\text{trx}}\\lambda\^2}{(4\\pi)\^2 r\^2(x)}g(x)=Pf(4π)2r2(x)Gtrxλ2 代入，得到 ##

\mathbb E[I_p(\ell)]
=\frac{1}{\Delta}\int g(x),dx

P\frac{G_{\text{trx}}\lambda^2}{(4\pi)2}\frac{f}{\Delta}

\int \frac{1}{r^2(x)}dx.

几何关系：若车道中心线与受害车道相距 RRR，且把沿道路方向的坐标写成 xxx，则 r2(x)=R2+x2. r\^2(x)=R\^2+x\^2. r2(x)=R2+x2. 同时，由FOV限制（只有进入视场的干扰才算），积分下限从某个 θ0=ϕℓ/2\\theta_0=\\phi_\\ell/2θ0=ϕℓ/2（半视场角）开始。用 x=Rtan⁡θx=R\\tan\\thetax=Rtanθ（即 θ=arctan⁡(x/R)\\theta=\\arctan(x/R)θ=arctan(x/R)）变换，dx=Rsec⁡2θ dθdx=R\\sec\^2\\theta\\,d\\thetadx=Rsec2θdθ，并且 1R2+x2=1R2(1+tan⁡2θ)=cos⁡2θR2. \\frac{1}{R\^2+x\^2}=\\frac{1}{R\^2(1+\\tan\^2\\theta)}=\\frac{\\cos\^2\\theta}{R\^2}. R2+x21=R2(1+tan2θ)1=R2cos2θ. 于是 ##

\int_{\theta_0}^{{\pi/2}\frac{1}{R}2+x^2}dx

\int_{\theta_0}^{{\pi/2}\frac{\cos}2\theta}{R^2}\cdot R\sec^2\theta,d\theta

=\frac{1}{R}\int_{\theta_0}^{\pi/2}1,d\theta

=\frac{\pi/2-\theta_0}{R}.

将 θ0=ϕℓ/2\\theta_0=\\phi_\\ell/2θ0=ϕℓ/2 代回，就得到式(9)那种"与 ϕℓ\\phi_\\ellϕℓ、RRR、Δ\\DeltaΔ 成简单比例"的结果形态（文中给的是同类化简表达式，并强调小 xxx 处需要安全边界避免奇异）。 *** ** * ** *** ### A.5 从式(10)到式(11)：把"可设计量"显式拆出来 式(10)给出 S=∣γ∣2Gp2,I≤f∣γint∣2GpGI. S=\|\\gamma\|\^2G_p\^2,\\qquad I\\le f\|\\gamma_{\\text{int}}\|\^2 G_p G_I. S=∣γ∣2Gp2,I≤f∣γint∣2GpGI. 于是 SIR≥∣γ∣2Gpf∣γint∣2GI. \\mathrm{SIR}\\ge \\frac{\|\\gamma\|\^2G_p}{f\|\\gamma_{\\text{int}}\|\^2 G_I}. SIR≥f∣γint∣2GI∣γ∣2Gp. 接下来用"目标回波由雷达方程决定、干扰由Friis决定"的功率比（式(7)）把 ∣γ∣2/∣γint∣2\|\\gamma\|\^2/\|\\gamma_{\\text{int}}\|\^2∣γ∣2/∣γint∣2 替换成与 σ,d,r\\sigma,d,rσ,d,r 有关的比例，再把 fff 展开成与占空比 uuu、斜率 a=B/Ta=B/Ta=B/T、ADC带宽 BsB_sBs、以及FOV（通过发生重叠的概率）相关的因子，就得到式(11)那种"第一因子不可控、第二因子可控"的结构。作者在正文里直接强调可控项包括：小占空比、小斜率（或小 B/BsB/B_sB/Bs 比例）、缩小FOV以减小 fff、以及增大有效处理增益 Gp/GIG_p/G_IGp/GI。