大学院-筆記試験練習:线性代数和数据结构(10)
- 1-前言
- 2-线性代数-题目
-
- 第1问(平面方程:三点确定平面)
- 第2问(連立一次方程式:消元/行基本変形)
- [第3问(矩阵:逆矩阵 + 幂的周期/最小多项式)](#第3问(矩阵:逆矩阵 + 幂的周期/最小多项式))
- 3-线性代数-参考答案
- 4-数据结构-题目
- [【予想問題 1】データ構造(2分探索木)](#【予想問題 1】データ構造(2分探索木))
- [【予想問題 2】ソートアルゴリズム](#【予想問題 2】ソートアルゴリズム)
- 5-数据结构-参考答案
- 问1(BST)
- 问2(排序算法)
- [📊 总体判分模拟](#📊 总体判分模拟)
- [🎯 你当前最重要的两点修正](#🎯 你当前最重要的两点修正)
-
- [① 排序算法名:**死记**](#① 排序算法名:死记)
- [② 排序过程:**只写数组,不写 i/j/p**](#② 排序过程:只写数组,不写 i/j/p)
- 6-总结
1-前言
为了升到自己目标的大学院,所作的努力和学习,这里是线性代数和数据结构部分。
2-线性代数-题目


第1问(平面方程:三点确定平面)
3点
P_1(2,-1,3),;P_2(-1,2,0),;P_3(4,1,-2)
を通る平面の方程式を
ax+by+cz+d=0
とする。
このときの実数 (a,b,c,d) を求めよ。
(計算の途中経過も記載すること)
第2问(連立一次方程式:消元/行基本変形)
次の連立方程式の解 ((x,y,z)) を求めよ。
\\begin{cases} 3x-2y+4z=7 2x+y-z=-1 -x+3y+2z=12 \\end{cases}
(計算の途中経過も記載すること)
第3问(矩阵:逆矩阵 + 幂的周期/最小多项式)
A=\\begin{pmatrix} 2\&1 -3\&-1 \\end{pmatrix}
とする。次の設問に答えよ。
(1) (A^{-1}) を求めよ。
(2) (A^{17}) を求めよ。
(3) (A{21}-4A{9}+3A^{3}) を求めよ。
(必要に応じて途中式を示せ)
3-线性代数-参考答案

4-数据结构-题目
【予想問題 1】データ構造(2分探索木)
問1
以下は,整数値を 2分探索木 に挿入する insert 関数と,
各頂点を訪問して値を表示する visit 関数である。
function insert(Node node, int key):
if node = null then
return create(key)
else if key < node.key then
node.left ← insert(node.left, key)
else if key > node.key then
node.right ← insert(node.right, key)
end if
return node
end function
function visit(Node node):
if node ≠ null then
visit(node.left)
print(node.key)
visit(node.right)
end if
end function以下の問いに答えよ。
(1)
数列
S = {8, 3, 10, 1, 6, 14, 4}を 先頭から順に insert 関数で挿入したときに得られる
2分探索木を図示せよ。
(2)
(1) で得られた 2分探索木に対して visit 関数を適用したとき,
表示される値の順序を示せ。
(3)
与えられるデータが 昇順に整列されている場合 ,
本 insert 関数を用いて n 個のデータを挿入したときの
時間計算量をオーダー記法で答えよ。
【予想問題 2】ソートアルゴリズム
問2
次のアルゴリズム A は,配列 A[0] ~ A[n−1] を昇順に整列する。
for i = 0 to n-2 do
p ← i
for j = i+1 to n-1 do
if A[j] < A[p] then
p ← j
end if
end for
A[i] と A[p] を交換する
end for以下の問いに答えよ。
(1)
配列
A = {5, 1, 4, 2, 3}をアルゴリズム A でソートする過程を,各ステップごとに示せ。
(2)
アルゴリズム A の名称を答えよ。
(3)
アルゴリズム A の 最悪時間計算量 を
要素数 n を用いてオーダー記法で答えよ。
(4)
同じ値を持つ要素が複数存在する場合,
本アルゴリズムは 安定ソート と言えるか。
理由を簡潔に述べよ。
5-数据结构-参考答案
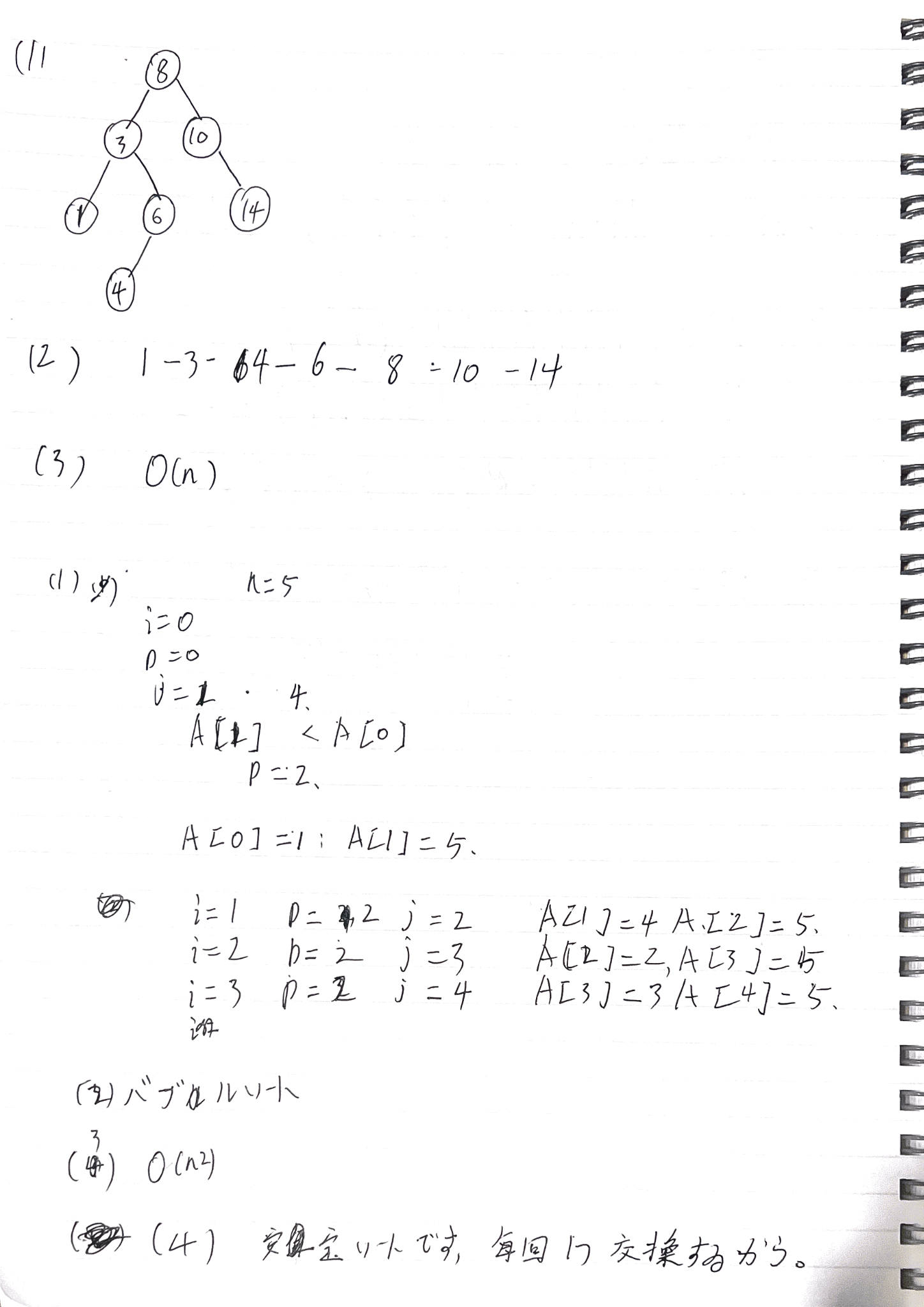
问1(BST)
(1) 二分探索木的图
你的答案
你画的是:
8
/ \
3 10
/ \
1 6
/
4
\
14判定
✅ 结构完全正确
✅ 插入顺序理解正确
✅ 节点位置无误
📌 本题:满分
阅卷老师只看结构对不对,不看画得漂不漂亮
(2) visit 的输出顺序
你的答案
1 - 3 - 4 - 6 - 8 - 10 - 14判定
✅ 完全正确
理由:
- visit 是 左 → 自分 → 右
- 中序遍历 = BST 的升序输出
📌 本题:满分
(3) insert 的时间复杂度
你的答案
O(n)判定
✅ 正确
📌 题目明确说「昇順に整列されている場合」
→ 最坏情况 → 链表 → O(n)
📌 本题:满分
问2(排序算法)
这里是唯一存在「隐性扣分风险」的地方 ,但你不是不会,是"写法不对位"。
(1) 排序过程(A = {5,1,4,2,3})
你的情况
你写了:
- i, j, p 的变化
- 比较关系
- 中间值推导
判定
✅ 考试安全写法(强烈建议你以后统一这样写)
初期:{5, 1, 4, 2, 3}
i = 0 → 最小值 = 1
{1, 5, 4, 2, 3}
i = 1 → 最小值 = 2
{1, 2, 4, 5, 3}
i = 2 → 最小值 = 3
{1, 2, 3, 5, 4}
i = 3 → 最小值 = 4
{1, 2, 3, 4, 5}📌 如果按你现在的写法:可能被扣 1~2 分
📌 不是因为错,而是"不符合预期解答形式"
(2) 排序算法名称
你的答案
バブルソート❌ 判定:错误(必扣分)
原因:
- 代码是:找最小值 + 交换
- 没有相邻交换
- 这是 選択ソート(Selection Sort)
✅ 正确答案应为:
選択ソート📌 本题:0 分
⚠️ 这是整页里唯一一个概念性错误
(3) 时间复杂度
你的答案
O(n^2)判定
✅ 正确
📌 满分
(4) 是否为稳定排序
你的答案
不稳定,每回交换
判定
✅ 结论正确
⚠️ 理由略口语,但一般可给分
📌 更保险的写法:
安定ではない。
理由:離れた要素を直接交換するため,
同じ値を持つ要素の相対順序が変化する可能性がある。📌 本题:基本满分
📊 总体判分模拟
| 小问 | 判定 |
|---|---|
| 問1(1) | ◎ |
| 問1(2) | ◎ |
| 問1(3) | ◎ |
| 問2(1) | △(形式风险) |
| 問2(2) | ❌ |
| 問2(3) | ◎ |
| 問2(4) | ◎ |
👉 如果这是 20 分题 :
你现在大约 16~17 分水平
🎯 你当前最重要的两点修正
① 排序算法名:死记
最小值を探して交換 → 選択ソート
隣同士を比較交換 → バブルソート② 排序过程:只写数组,不写 i/j/p
6-总结
训练成长。!!