一题N解 两种分块|四维莫队|容斥+二维莫队|希尔伯特排序莫队|zorder排序莫队

一条大祥脚2026-01-18 8:38

D. Strange Queries

分块1

两个区间查，一个经典思路是，对两个区间分别分块，然后维护块对块的贡献，也就是预处理 f ( i , j ) f(i,j) f(i,j)表示一个序列的第 i i i个块，和另一个序列的前 j j j个块的答案，这样，对于两个区间查，其中整块和整块的答案，就可以枚举其中一个区间的所有整块，然后前缀和查询，和另一个区间的所有整块的答案。

这个做法有很强的拓展性，本题的两个区间都是在一个序列上的，实际上完全可以是两个不同的序列 a , b a,b a,b，上分别查两个区间 [ l a , r a ] [ l b , r b ] [l_a,r_a][l_b,r_b] [la,ra][lb,rb]的答案

整体思路是

  • 整块对整块的贡献，枚举一个区间 [ l 1 , r 1 ] [l_1,r_1] [l1,r1]内的整块，用 f ( i , j ) f(i,j) f(i,j)这个前缀和数组，查询每个整块，和 [ l 2 , r 2 ] [l_2,r_2] [l2,r2]内的整块的答案
  • 散点和散点的答案，把 [ l 1 , r 1 ] [l_1,r_1] [l1,r1]内的散点加入桶，然后枚举 [ l 2 , r 2 ] [l_2,r_2] [l2,r2]的散点，查询桶即可。类似于枚举右维护左的思路。
  • 散点和整块的答案，包含区间1的散点和区间2的整块，区间2的散点和区间1的整块两种，本质是一样的。我们目前预处理的数组无法回答，考虑增加一个预处理， g ( i , j ) g(i,j) g(i,j)保存值为 i i i的元素，在前 j j j个整块内的出现次数，这需要 O ( n n ) O(n\sqrt n) O(nn )空间，对于本题 n = 5 e 4 n=5e4 n=5e4的空间，可以接受。然后枚举散点，查询前缀和数组即可得到散点对整块的答案。

实现时，需要分类讨论区间1，2是不是至少包含一个整块。

c 复制代码 
struct block {
	int a[N];
	int st[N], ed[N], pos[N];
	int tmp[N], f[300][300], g[N][300];
	int B;
 
	void init(int n, vi &A) {
		B = sqrt(n);
		for (int i = 0; i < n; i++) {
			a[i] = A[i];
			pos[i] = i / B;
			ed[pos[i]] = i;
		}
		for (int i = n - 1; i >= 0; i--) {
			st[pos[i]] = i;
		}
 
		int num = (n + B - 1) / B;
		for (int i = 0; i < num; i++) {
			for (int j = st[i]; j <= ed[i]; j++) {
				tmp[a[j]]++;
			}
			for (int j = 0; j < num; j++) {
				int cur = 0;
				for (int k = st[j]; k <= ed[j]; k++) {
					cur += tmp[a[k]];
				}
				f[i][j] = cur;
			}
			for (int j = 1; j <= n; j++) {
				g[j][i] = tmp[j];
			}
			for (int j = st[i]; j <= ed[i]; j++) {
				tmp[a[j]]--;
			}
		}
		for (int i = 0; i < num; i++) {
			for (int j = 1; j < num; j++) {
				f[i][j] += f[i][j - 1];
			}
		}
		for (int i = 1; i <= n; i++) {
			for (int j = 1; j < num; j++) {
				g[i][j] += g[i][j - 1];
			}
		}
 
	}
 
	int ask(int l1, int r1, int l2, int r2) {
		int res = 0;
		int p1 = pos[l1], q1 = pos[r1];
		int p2 = pos[l2], q2 = pos[r2];
//		cout << p1 << ' ' << q1 << ' ' << p2 << ' ' << q2 << '\n';
 
		if (p1 == q1) {
			if (p2 == q2) {
				for (int i = l1; i <= r1; i++) {
					tmp[a[i]]++;
				}
				for (int i = l2; i <= r2; i++) {
					res += tmp[a[i]];
				}
				for (int i = l1; i <= r1; i++) {
					tmp[a[i]]--;
				}
			} else {
				for (int i = l1; i <= r1; i++) {
					int x = a[i];
					tmp[x]++;
					res += g[x][q2 - 1] - g[x][p2];
				}
 
				for (int i = l2; i <= ed[p2]; i++) {
					res += tmp[a[i]];
				}
 
				for (int i = st[q2]; i <= r2; i++) {
					res += tmp[a[i]];
				}
				for (int i = l1; i <= r1; i++) {
					tmp[a[i]]--;
				}
			}
		} else {
			if (p2 == q2) {
				for (int i = l1; i <= ed[p1]; i++) {
					int x = a[i];
					tmp[x]++;
				}
				for (int i = st[q1]; i <= r1; i++) {
					int x = a[i];
					tmp[x]++;
				}
 
				for (int i = l2; i <= r2; i++) {
					int x = a[i];
					res += tmp[x];
					res += g[x][q1 - 1] - g[x][p1];
				}
 
				for (int i = l1; i <= ed[p1]; i++) {
					tmp[a[i]]--;
				}
				for (int i = st[q1]; i <= r1; i++) {
					tmp[a[i]]--;
				}
			} else {
				for (int i = l1; i <= ed[p1]; i++) {
					int x = a[i];
					tmp[x]++;
					res += g[x][q2 - 1] - g[x][p2];
				}
				for (int i = st[q1]; i <= r1; i++) {
					int x = a[i];
					tmp[x]++;
					res += g[x][q2 - 1] - g[x][p2];
				}
 
				for (int i = l2; i <= ed[p2]; i++) {
					int x = a[i];
					res += tmp[x];
					res += g[x][q1 - 1] - g[x][p1];
				}
				for (int i = st[q2]; i <= r2; i++) {
					int x = a[i];
					res += tmp[x];
					res += g[x][q1 - 1] - g[x][p1];
				}
 
				for (int i = l1; i <= ed[p1]; i++) {
					tmp[a[i]]--;
				}
				for (int i = st[q1]; i <= r1; i++) {
					tmp[a[i]]--;
				}
				for (int i = p1 + 1; i <= q1 - 1; i++) {
					res += f[i][q2 - 1] - f[i][p2];
				}
			}
		}
		return res;
	}
} b;
void solve() {
	int n;
	cin >> n;
 
	vi a(n);
	for (int &x : a) {
		cin >> x;
	}
	b.init(n, a);
	int m;
	cin >> m;
	rep(i, 1, m) {
		int l1, r1, l2, r2;
		cin >> l1 >> r1 >> l2 >> r2;
		cout << b.ask(l1 - 1, r1 - 1, l2 - 1, r2 - 1) << '\n';
	}
 
}

分块2

上一个分块做法，我们把贡献拆成了多部分，具体就是我们把一个区间的整块，对另一个区间的贡献，细分成了整块对整块，整块对散点，有点麻烦。

一个优化思路是，既然我们都用上空间复杂度 O ( n n ) O(n\sqrt n) O(nn )的前缀和了，为什么不干脆维护块对整个序列的前缀和，这样空间复杂度也是 O ( n n ) O(n\sqrt n) O(nn )的，但区间1的整块，和区间2的答案，就只不用拆成两部分，可以用这个前缀和一次算完

具体来说，答案分成

  • 散点对散点的贡献，和前一个做法一样，一个区间的散点用桶计数，枚举另一个区间的散点，查桶计算贡献
  • 区间1的整块和区间2整体的贡献，维护一个 f ( i , j ) f(i,j) f(i,j)表示第 i i i个块，和序列前 j j j个元素的答案，那么块 i i i和区间2的答案可以 f ( i , r 2 ) − f ( i , l 2 − 1 ) f(i,r_2)-f(i,l_2-1) f(i,r2)−f(i,l2−1)前缀和算出，且不用区分整块和整块，整块和散点两部分，一次性计算完了
  • 区间1的散点和区间2的整块的贡献，枚举区间2的整块，同样前缀和，可以计算每个整块，和区间1的散点区间的答案。

代码实现比上一个做法短很多，注意为了降低常数，预处理了每个位置 i i i所在的块编号 p o s pos pos，每个块的起点和终点 s t , e d st,ed st,ed

c 复制代码 
struct block {
	int a[N];
	int st[N], ed[N], pos[N];
	int tmp[N], f[300][N];
	int B;
 
	void add(int l, int r, int v) {
		for (int i = l; i <= r; i++) {
			tmp[a[i]] += v;
		}
	}
	void init(int n, vi &A) {
		B = sqrt(n);
		for (int i = 1; i <= n; i++) {
			a[i] = A[i];
			pos[i] = i / B;
			ed[pos[i]] = i;
		}
		for (int i = n; i >= 1; i--) {
			st[pos[i]] = i;
		}
 
		int num = (n + B - 1) / B;
		for (int i = 0; i < num; i++) {
			for (int j = st[i]; j <= ed[i]; j++) {
				tmp[a[j]]++;
			}
			for (int j = 1; j <= n; j++) {
				f[i][j] = tmp[a[j]] + f[i][j - 1];
			}
			for (int j = st[i]; j <= ed[i]; j++) {
				tmp[a[j]]--;
			}
		}
 
	}
 
	int ask(int l1, int r1, int l2, int r2) {
		int res = 0;
		int p1 = pos[l1], q1 = pos[r1];
		int p2 = pos[l2], q2 = pos[r2];
//		cout << p1 << ' ' << q1 << ' ' << p2 << ' ' << q2 << '\n';
 
		if (p1 == q1) {
			add(l1, r1, 1);
			if (p2 == q2) {
				for (int i = l2; i <= r2; i++) {
					res += tmp[a[i]];
				}
			} else {
				for (int i = l2; i <= ed[p2]; i++) {
					res += tmp[a[i]];
				}
				for (int i = st[q2]; i <= r2; i++) {
					res += tmp[a[i]];
				}
				for (int i = p2 + 1; i <= q2 - 1; i++) {
					res += f[i][r1] - f[i][l1 - 1];
				}
			}
			add(l1, r1, -1);
		} else {
			add(l1, ed[p1], 1);
			add(st[q1], r1, 1);
			if (p2 == q2) {
				for (int i = l2; i <= r2; i++) {
					res += tmp[a[i]];
				}
			} else {
				for (int i = l2; i <= ed[p2]; i++) {
					res += tmp[a[i]];
				}
				for (int i = st[q2]; i <= r2; i++) {
					res += tmp[a[i]];
				}
 
				for (int i = p2 + 1; i <= q2 - 1; i++) {
					res += f[i][ed[p1]] - f[i][l1 - 1];
					res += f[i][r1] - f[i][st[q1] - 1];
				}
			}
			for (int i = p1 + 1; i <= q1 - 1; i++) {
				res += f[i][r2] - f[i][l2 - 1];
			}
			add(l1, ed[p1], -1);
			add(st[q1], r1, -1);
		}
		return res;
	}
} b;
void solve() {
	int n;
	cin >> n;
 
	vi a(n + 1);
	for (int i = 1; i <= n; i++) {
		cin >> a[i];
	}
	b.init(n, a);
	int m;
	cin >> m;
	rep(i, 1, m) {
		int l1, r1, l2, r2;
		cin >> l1 >> r1 >> l2 >> r2;
		cout << b.ask(l1, r1, l2, r2) << '\n';
	}
 
}

四维莫队

如果一个区间询问，可以抽象成二维空间内的点，然后莫队。两个区间，也可以抽象成四维空间内的点，然后莫队，只是 k k k维莫队时间复杂度为 O ( n ( 2 k − 1 ) / k ) O(n^{(2k-1)/k}) O(n(2k−1)/k)，块长 n ( k − 1 ) / k n^{(k-1)/k} n(k−1)/k。

并且本题，虽然我们把 l 1 , r 1 , l 2 , r 2 l_1,r_1,l_2,r_2 l1,r1,l2,r2看成四维的了，但他们实际上维护的还是两个区间，所以辅助数组要维护两组，同样也需要两套 a d d , d e l add,del add,del来分别执行 l 1 , r 1 l_1,r_1 l1,r1和 l 2 , r 2 l_2,r_2 l2,r2的指针移动

c 复制代码 
void solve() {
	int n;
	cin >> n;
	int B = pow(n, 0.75);
	vi a(n + 1), c1(n + 1), c2(n + 1);
	rep(i, 1, n) {
		cin >> a[i];
	}
 
	int q;
	cin >> q;
 
	vvi Q;
	rep(i, 1, q) {
		int l1, r1, l2, r2;
		cin >> l1 >> r1 >> l2 >> r2;
		Q.push_back({l1, r1, l2, r2, i});
	}
 
	sort(Q.begin(), Q.end(), [&](vi & x, vi & y) {
		vi xx = {x[0] / B, x[1] / B, x[2] / B, x[3]};
		vi yy = {y[0] / B, y[1] / B, y[2] / B, y[3]};
		return xx < yy;
	});
 
	int cl1 = 1, cr1 = 0, cl2 = 1, cr2 = 0;
	int ans = 0;
	auto add1 = [&](int x)->void{
		ans += c2[a[x]];
		c1[a[x]]++;
	};
	auto del1 = [&](int x)->void{
		ans -= c2[a[x]];
		c1[a[x]]--;
	};
	auto add2 = [&](int x)->void{
		ans += c1[a[x]];
		c2[a[x]]++;
	};
	auto del2 = [&](int x)->void{
		ans -= c1[a[x]];
		c2[a[x]]--;
	};
	vi res(q + 1);
	for (auto &t : Q) {
		int l1 = t[0], r1 = t[1], l2 = t[2], r2 = t[3], id = t[4];
		while (cl1 > l1)
			add1(--cl1);
		while (cr1 < r1)
			add1(++cr1);
		while (cl1 < l1)
			del1(cl1++);
		while (cr1 > r1)
			del1(cr1--);
		while (cl2 > l2)
			add2(--cl2);
		while (cr2 < r2)
			add2(++cr2);
		while (cl2 < l2)
			del2(cl2++);
		while (cr2 > r2)
			del2(cr2--);
 
 
		res[id] = ans;
	}
 
	rep(i, 1, q) {
		cout << res[i] << '\n';
	}
}

容斥+二维莫队

我们把四维问题降低到二维，采用类似二位前缀和的容斥，一个 [ l 1 , r 1 ] [ l 2 , r 2 ] [l1,r1][l2,r2] [l1,r1][l2,r2]的四维问题，实际上等价于 [ 1 , r 1 ] [ 1 , r 2 ] − [ 1 , l 1 − 1 ] [ 1 , r 2 ] − [ 1 , r 1 ] [ 1 , l 2 − 1 ] + [ 1 , l 1 − 1 ] [ 1 , l 2 − 1 ] [1,r_1][1,r_2]-[1,l_1-1][1,r_2]-[1,r_1][1,l_2-1]+[1,l_1-1][1,l_2-1] [1,r1][1,r2]−[1,l1−1][1,r2]−[1,r1][1,l2−1]+[1,l1−1][1,l2−1]，四个问题的和。对于这里的每个问题，都可以用普通的二维莫队来解决。也就是把一个 [ 1 , x ] [ 1 , y ] [1,x][1,y] [1,x][1,y]看成 [ x , y ] [x,y] [x,y]的二维问题。

同样需要注意，这个 ( x , y ) (x,y) (x,y)的二维问题，不像一般的莫队，维护的是区间 [ x , y ] [x,y] [x,y]的信息，而是维护的 [ 1 , x ] [ 1 , y ] [1,x][1,y] [1,x][1,y]的信息，实际上是两个区间，所以要两套辅助数组，两套 a d d , d e l add,del add,del，并且 x , y x,y x,y这两个点的移动逻辑，都是区间右端点的逻辑，而不是一个左端点一个右端点。

然后本题的询问排序方式，我们不采用分块排序，而是实验一个新的排序：希尔伯特排序，也就是在一个平面上画一个希尔伯特曲线，然后平面上每个点都在这条曲线上，可以计算出，每个点，是曲线上从一端开始的第几个点，或者说到曲线端点的距离，以此为关键字升序排序，然后跑莫队即可。

希尔伯特曲线是一个分型曲线，也就是递归定义的，每一阶都把空间划分成四个区域，然后每个区域内也是一个希尔伯特曲线，三阶段大概长这样， d d d阶的希尔伯特曲线，可以填充 2 d ∗ 2 d 2^d*2^d 2d∗2d的平面

这个排序方式的上界也是 O ( n n ) O(n\sqrt n) O(nn )的，但是局部性比分块要好，也就是排序后相邻的点，在平面上距离也不会太远，指针移动次数较少，最后跑莫队也就常数较小。

c 复制代码 
long long hilbertOrder(int x, int y, int k = 16) {
	long long d = 0;
	for (int s = 1 << (k - 1); s > 0; s >>= 1) {
		bool rx = x & s;
		bool ry = y & s;
		// 核心逻辑：当前象限相对于中心点的位置，并累计距离
		d += s * 1LL * s * ((3 * rx) ^ ry);
 
		// 如果是在特定的两个象限，需要进行坐标变换（镜像/旋转）
		if (!ry) {
			if (rx) {
				x = (1 << k) - 1 - x;
				y = (1 << k) - 1 - y;
			}
			swap(x, y);
		}
	}
	return d;
}
void solve() {
	int n;
	cin >> n;
	vi a(n + 1), idx(n + 1);
	vi c1(n + 1), c2(n + 1);
	int B = sqrt(n);
	rep(i, 1, n) {
		cin >> a[i];
		idx[i] = i / B;
	}
	int m;
	cin >> m;
 
	vector<array<int, 5>>q;
	q.reserve(4 * m);
	rep(i, 1, m) {
		int l1, r1, l2, r2;
		cin >> l1 >> r1 >> l2 >> r2;
		auto add_q = [&](int x, int y, int op, int id) {
			if (x < 0 || y < 0) return;
			q.push_back({x, y, op, id, hilbertOrder(x, y)});
		};
		add_q(r1, r2, 1, i);
		add_q(l1 - 1, l2 - 1, 1, i);
		add_q(l1 - 1, r2, -1, i);
		add_q(r1, l2 - 1, -1, i);
	}
	sort(q.begin(), q.end(), [&](auto & x, auto & y) {
		return x[4] < y[4];
	});
 
	int ans = 0, l = 1, r = 0;
	auto add1 = [&](int i)->void{
		c1[a[i]]++;
		ans += c2[a[i]];
	};
	auto del1 = [&](int i)->void{
		c1[a[i]]--;
		ans -= c2[a[i]];
	};
	auto add2 = [&](int i)->void{
		c2[a[i]]++;
		ans += c1[a[i]];
	};
	auto del2 = [&](int i)->void{
		c2[a[i]]--;
		ans -= c1[a[i]];
	};
 
	vi res(m + 1);
	for (auto [x, y, op, id, _] : q) {
		while (l < x)add1(++l);
		while (l > x)del1(l--);
		while (r < y)add2(++r);
		while (r > y)del2(r--);
 
		res[id] += op * ans;
	}
 
	rep(i, 1, m) {
		cout << res[i] << '\n';
	}
}

Zorder

也是一个莫队排序方式，上界也是 O ( n n ) O(n\sqrt n) O(nn )，常数也很小。和希尔伯特曲线类似，也是一个分形曲线，并且局部性也比分块要好，计算大概是把 x , y x,y x,y两个数的二进制中间填充0，然后交错地查在一起。曲线形状大概是这样

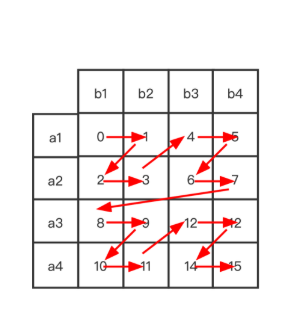
每一层都在走 z z z字型，因此得名 Z o r d e r Zorder Zorder

局部性比希尔伯特略差，但优点是， z o r d e r zorder zorder函数值计算，用 O ( 1 ) O(1) O(1)位运算优化分治的话，分治地每一层都只需要 O ( 1 ) O(1) O(1)时间，因此整体复杂度只需要 O ( log ⁡ log ⁡ V ) O(\log\log V) O(loglogV)，比希尔伯特 O ( log ⁡ V ) O(\log V) O(logV)更快。

c 复制代码 
// 核心函数：将 32 位整数的二进制位扩展，每两位之间插入一个 0
// 输入 n 的范围: 0 到 2^32 - 1
// 输出返回一个 64 位整数，其位分布在 A_B_C_D... 模式中
ull part(ull n) {
    n &= 0x00000000FFFFFFFF; // 确保只有低 32 位有效
    n = (n | (n << 16)) & 0x0000FFFF0000FFFF;
    n = (n | (n << 8))  & 0x00FF00FF00FF00FF;
    n = (n | (n << 4))  & 0x0F0F0F0F0F0F0F0F;
    n = (n | (n << 2))  & 0x3333333333333333;
    n = (n | (n << 1))  & 0x5555555555555555;
    return n;
}
 
// 计算 Z-order (Morton Code)
ull getZOrder(int x, int y) {
    // 将 x 放在偶数位，y 放在奇数位（或者反过来，不影响排序性质）
    return part(x) | (part(y) << 1);
}
typedef unsigned int uint32;
 
// 针对 16 位整数的位扩展函数
// 将 16 位整数扩展为 32 位，在相邻位之间插入 0
// 例如：二进制 1111 -> 10101010
uint32 part16(uint32 n) {
    n &= 0x0000FFFF;                  // 确保只处理低 16 位
    n = (n | (n << 8)) & 0x00FF00FF;  // 拉开 8 位
    n = (n | (n << 4)) & 0x0F0F0F0F;  // 每 4 位拉开
    n = (n | (n << 2)) & 0x33333333;  // 每 2 位拉开
    n = (n | (n << 1)) & 0x55555555;  // 每 1 位拉开，完成稀释
    return n;
}
 
// 计算 16 位坐标的 Z-order (结果为 32 位)
uint32 getZOrder16(int x, int y) {
    return part16(x) | (part16(y) << 1);
}
void solve() {
	int n;
	cin >> n;
	vi a(n + 1), idx(n + 1);
	vi c1(n + 1), c2(n + 1);
	int B = sqrt(n);
	rep(i, 1, n) {
		cin >> a[i];
		idx[i] = i / B;
	}
	int m;
	cin >> m;
 
	vector<array<int, 5>>q;
	q.reserve(4 * m);
	rep(i, 1, m) {
		int l1, r1, l2, r2;
		cin >> l1 >> r1 >> l2 >> r2;
		auto add_q = [&](int x, int y, int op, int id) {
			if (x < 0 || y < 0) return;
			q.push_back({x, y, op, id, getZOrder16(x, y)});
		};
		add_q(r1, r2, 1, i);
		add_q(l1 - 1, l2 - 1, 1, i);
		add_q(l1 - 1, r2, -1, i);
		add_q(r1, l2 - 1, -1, i);
	}
	sort(q.begin(), q.end(), [&](auto & x, auto & y) {
		return x[4] < y[4];
	});
 
	int ans = 0, l = 1, r = 0;
	auto add1 = [&](int i)->void{
		c1[a[i]]++;
		ans += c2[a[i]];
	};
	auto del1 = [&](int i)->void{
		c1[a[i]]--;
		ans -= c2[a[i]];
	};
	auto add2 = [&](int i)->void{
		c2[a[i]]++;
		ans += c1[a[i]];
	};
	auto del2 = [&](int i)->void{
		c2[a[i]]--;
		ans -= c1[a[i]];
	};
 
	vi res(m + 1);
	for (auto [x, y, op, id, _] : q) {
		while (l < x)add1(++l);
		while (l > x)del1(l--);
		while (r < y)add2(++r);
		while (r > y)del2(r--);
 
		res[id] += op * ans;
	}
 
	rep(i, 1, m) {
		cout << res[i] << '\n';
	}
}
相关推荐
Remember_9931 小时前
【数据结构】二叉树：从基础到应用全面解析
java·数据结构·b树·算法·leetcode·链表
2501_940315262 小时前
蓝桥云课：分巧克力（二分查找法）
数据结构·c++·算法
csuzhucong2 小时前
2种闪蝶魔方（待更新）
算法
C++chaofan2 小时前
JUC并发编程：LockSupport.park() 与 unpark() 深度解析
java·开发语言·c++·性能优化·高并发·juc
行稳方能走远2 小时前
Android C++ 学习笔记5
android·c++
乌萨奇也要立志学C++2 小时前
【Linux】信号量 信号量详解与应用和基于环形队列实现单 / 多生产消费模型
linux·c++
我是小疯子662 小时前
C++图论：从基础到实战应用
java·c++·图论
Swift社区2 小时前
LeetCode 377 组合总和 Ⅳ
算法·leetcode·职场和发展
漫随流水2 小时前
leetcode算法（404.左叶子之和）
数据结构·算法·leetcode·二叉树
热门推荐
01GitHub 镜像站点022025 Telegram 最新免费社工库机器人（LetsTG可[特殊字符]）搭建指南（含 Python 脚本）032025年大语言模型技术全景报告04Linux下V2Ray安装配置指南05安娜的档案(Anna’s Archive) 镜像网站/国内最新可访问入口（持续更新）06Claude Code Skills 实用使用手册07UV安装并设置国内源08Labelme从安装到标注：零基础完整指南09AI 规范驱动开发“三剑客”深度对比：Spec-Kit、Kiro 与 OpenSpec 实战指南10BongoCat - 跨平台键盘猫动画工具