字符串匹配：暴力法和KMP算法（C语言）

日拱一卒——功不唐捐2026-02-09 9:44

文章目录

KMP算法

1.串的定义

串（字符串）是一种特殊的线性表，其数据元素是字符。它是计算机中处理文本信息的基本数据结构。

char str[]="Hello world"

数据结构的串没有"\0",不同的编程语言，是否用"0°作为串的结束标志，是没有定论的，通过length来约束空间的长度也会更通用。

1.1定长顺序存储和变长分配存储表示

c 复制代码 
typedef struct {

char str[maxSize+1]；//从0号索引l存储数据，+1是为了存储\0（可选）
int length;
    
}

typedef struct {
    char *str;
    int length;
//动态分配空间
}

1.2 串的初始化

与普通变量赋值操作不同，串的赋值操作不能直接用=来实现，通过定义初始化函数来实现空间拷

贝。

c 复制代码 
//串头，初始化字符串
int strAssign(StrType *str, const char *ch);

申请多两个

0号不填：KMP监视哨

'\0'还要填

c 复制代码 
// tinaStr.h
#pragma once

typedef struct {
    char *str;
    int length;
} StrType;

// 字符串赋值，将ch指向的C字符串复制给str
void strAssign(StrType *str, const char *ch);
void releaseStr(StrType *str);
int index_simple(const StrType *str,const StrType *subStr);
c 复制代码 
#include "tinaStr.h"
#include <stdlib.h>  // 为了 malloc 和 free

void strAssign(StrType *str, const char *ch) {
    // 如果str已经分配了内存，先释放
    if (str->str) {
        free(str->str);
        str->str = NULL;
    }

    // 计算ch的长度
    int len = 0;
    while (ch[len]) {
        ++len;
    }

    // 如果长度为0，则str为空串
    if (len == 0) {
        str->str = NULL;
        str->length = 0;
        return;
    }

    // 分配内存，长度为len+1（包括结束符'\0'）
    str->str = (char *)malloc(sizeof(char) * (len + 2));
    if (!str->str) {
        // 内存分配失败，可以处理错误，这里简单地将长度置0并返回
        str->length = 0;
        return;
    }

    // 复制字符，包括结束符
    for (int i = 0; i <= len; ++i) {
        str->str[i+1] = ch[i];
    }
    str->length = len;
}

void releaseStr(StrType *str) {
    if （str）{   
        if （str->str）{
            free(str->str);
    }
              
 }

2.串的匹配

字符串匹配：在主串中找到与模式串相同的子串，并返回其所在位置。

2.1 暴力查找

假设法

c 复制代码 
int index_simple(const StrType *str, const StrType *subStr) {
    int i = 1;
    int j = 1;
    int k = i; // 记录起始位置

    while (i <= str->length && j <= subStr->length) {
        if (str->str[i] == subStr->str[j]) {
            i++;
            j++;
        } else {
            j = 1;
            k++;
            i = k;
        }
    }
    
    if (j > subStr->length) {
        return k; // 匹配成功，返回起始位置
    }
    
    return 0; // 匹配失败
}

// 测试函数
void test01(const StrType *str, const StrType *pattern) {
    int res = index_simple(str, pattern);
    printf("simple find index: %d\n", res);
}


int main() {
    StrType str;
    StrType subStr;

    str.str = NULL;
    subStr.str = NULL;

    strAssign(&str, "ABCDABCABCABABCABCD");
    strAssign(&subStr, "ABCABCD");

    // 调用测试函数
    test01(&str, &subStr);

    releaseStr(&str);
    releaseStr(&subStr);
    
    return 0;
}

2.2 KMP算法

不匹配的字符之前，一定是和模式串一致的，是否可以从这个已知信息来确定模式失配时，下次从模式串的第几个位置

  • 假设模式串为"abcabd "，主串为"abcabxxxx"
    • 从主串s[1]开始匹配时，在p[6]时失配
    • 既然在p[6]处失配，那么说明s[1:5]的信息一定是模式串的p[1:5]，所以按照朴素匹配算s[2]、s[3」... 开始匹配尝试，是不是可以明确肯定不会成功。
    • 而从s[4]开始，有可能成功
    • P[1:5]="abcab"，它的前缀（不包括自身）有："a", "ab", "abc", "abca"
    • P[1:5]="abcab"后缀（不包括自身）
      有："b", "ab", "cab", "bcab"。最长的公共前后缀是"ab"，长度为2
  1. 第一次匹配（从 s[1] 开始）
tex 复制代码 
匹配成功前5个字符：
主串： a b c a b x x x x
       ↑ ↑ ↑ ↑ ↑ × ← s[6] ≠ p[6] (x ≠ d)
模式： a b c a b d
       ↑ ↑ ↑ ↑ ↑ ↑
       1 2 3 4 5 6

已匹配部分：s[1:5] = abcab = p[1:5]
  1. 朴素算法的做法（试每个位置）

❌ 从 s[2] 开始匹配

text

复制代码 
主串： a b c a b x x x x
         ↑ ← 从这里开始对齐p[1]
模式：   a b c a b d
         ↑
         1

需要满足：s[2] = p[1] = a
但已知：s[2] = b
所以：❌ 必定失败！

为什么已知s[2]=b？
因为s[2]在第一次匹配时已经看过！

❌ 从 s[3] 开始匹配

tex 复制代码 
主串： a b c a b x x x x
           ↑ ← 从这里开始对齐p[1]
模式：     a b c a b d
           ↑
           1

需要满足：s[3] = p[1] = a
但已知：s[3] = c
所以：❌ 必定失败！
  1. ✅ 从 s[4] 开始可能成功
tex 复制代码 
主串： a b c a b x x x x
             ↑ ← 从这里开始对齐p[1]
模式：       a b c a b d
             ↑
             1

需要满足：s[4] = p[1] = a
已知：s[4] = a ✅ 满足！

继续检查：
主串： a b c a b x x x x
             ↑ ↑ ← 检查p[2]
模式：       a b c a b d
             ↑ ↑
             1 2

需要满足：s[5] = p[2] = b
已知：s[5] = b ✅ 满足！

到这里已经匹配了前2个字符，可能继续成功。
KMP算法的思想
  • 当子串和模式串不匹配 时，主串指针i不回溯 ，通过改变模式串指针j的值，来确定子串从失配处和模式串的哪个位置进行比较，因为模式串前面的信息在前面比较的时候已经知道信息了。
  • 如果能够存储子串失配后从模式串的哪个位置上进行比较，就可以实现KMP算法，故引入next数组，专门存放这个值。
  • 显然，next数组里的值，只跟模式串有关，因为模式串前面已经成功匹配的字符，就表示子串中已经包含了这些字符。
手动算next数组

  • next数组：Next数组记录的是模式串每个位置**"最长相同前后缀"的长度**。当匹配失败时，模式串要往前退多少才能继续匹配，而不是傻傻地只退1位。

  • 串的前缀：包含第一个字符，且不包含最后一个字符的子串

  • 串的后缀：包含最后一个字符，且不包含第一个字符的子串

tex 复制代码 
找前缀和后缀中相同的部分，取最长的那个。

还是 "abcab"：

    前缀：a, ab, abc, abca

    后缀：b, ab, cab, bcab

    相同的：只有 "ab"（长度=2）

    所以：最长相同前后缀长度 = 2

  • 当第j个字符匹配失败，由前[1，j-1]个字符组成的串记为S，手动计算就是根据这个S来决定的

  • next[j的值：S最长相等前后缀的长度+1，表示对于子串中前j-1个字符而言

  • 步骤

    1. 规则1：第一个字符的 Next 值 = 0，因为前面没有字符了。
    2. 规则2：后面的字符按以下公式：next[j] = (前j-1个字符的串)的最长相同前后缀长度 + 1

一句话解释：

已经匹配成功的部分如果有相同前后缀，前缀部分肯定也能匹配，所以跳过它们，直接从相同部分的下一个开始比较。

举例 ：

模式串：abcabd

在 p[6] 失败时：

  • 前5个字符 abcab 已匹配
  • abcab 有相同前后缀 ab（长度2）
  • 前缀 ab 肯定能匹配 （因为后缀 ab 已匹配）
  • 所以直接从 p[3] 开始比较（2+1）

next[6] = 2 + 1 = 3

意思：跳过前2个字符，从第3个开始

为什么 +1？

  • 长度2表示：有2个字符肯定匹配
  • 但我们要比较的是下一个字符
  • 所以是：已确定的匹配数 + 要检查的下一个位置
next数组值的规律
  • next[j]的值每次最多增加1
  • 模式串的最后一位字符不影响next数组的结果
  • next数组的定义：当主串与模式串的某一位字符不匹配时，模式串要回退到的位置


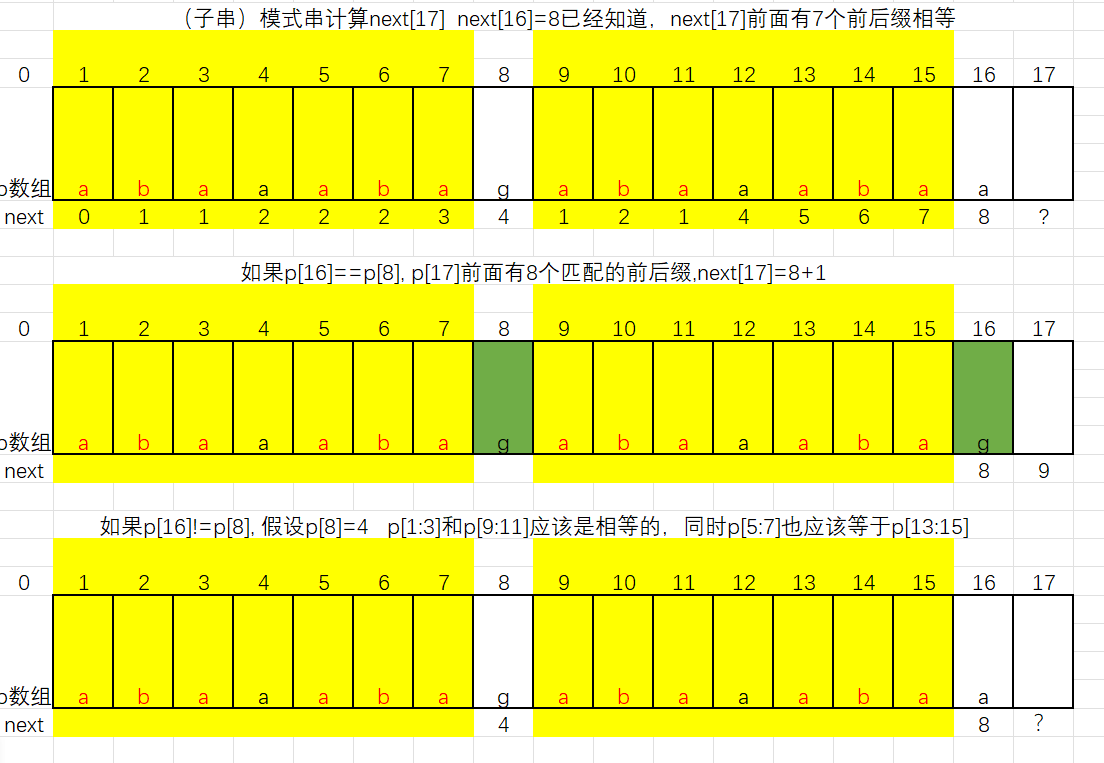
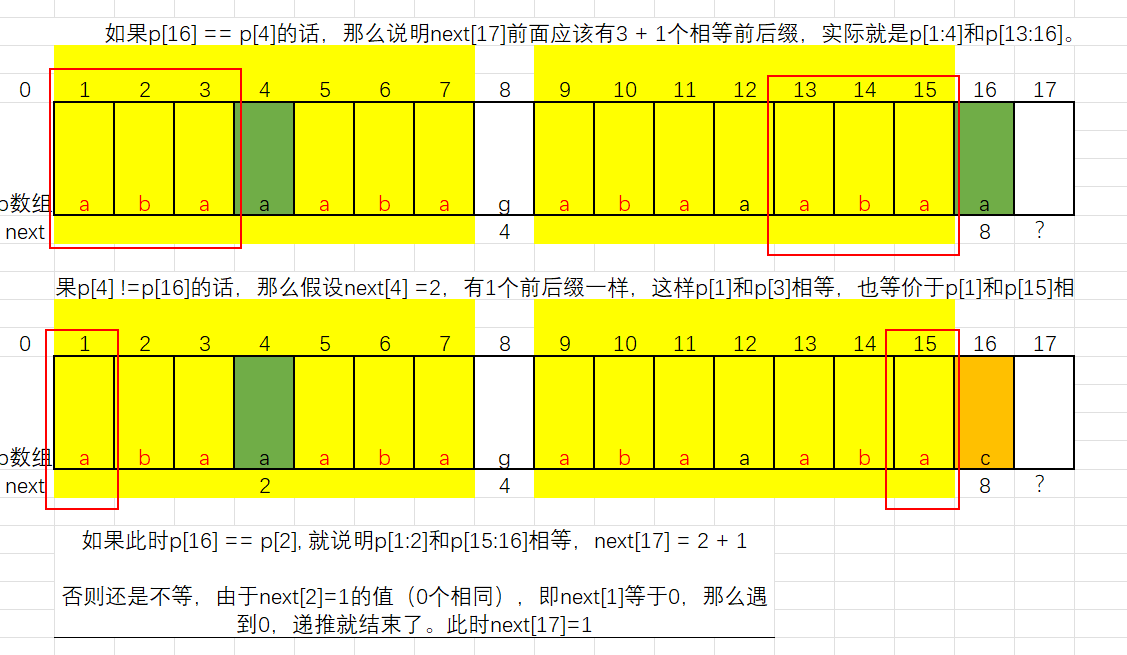
c 复制代码 
void getNext(StrType *subStr, int next[]) {
	int i = 1, j = 0; // 串从数组下标1位置开始存储
    //i 模式串（短串）的位置
    //j next数组值
	next[0] = 0;
    while (i < subStr->length)
    {
        
        if (j == 0 || subStr->str[i] == subStr->str[j]) {
            ++i;
            ++j;
            next[i] = j;
        } 
        else 
        {
            //不等往前看
            j = next[j];
        }

    }
}
代码
c 复制代码 
void getNext(StrType *subStr, int next[]) {
    //next 填的为公共 前后缀长度加一
	int i = 1, j = 0; // 串从数组下标1位置开始存储
    //i 模式串（短串）的位置
    //j next数组值
	next[0] = 0;
    //i = length 时，不会进入循环  next索引最大为length
    while (i < subStr->length)
    {
        
        if (j == 0 || subStr->str[i] == subStr->str[j]) {
            ++i;
            ++j;
            next[i] = j;
        } 
        else 
        {
            //不等往前看
            j = next[j];
        }

    }
}

// KMP模式匹配算法
int indexKMP(const StrType *str, const StrType *subStr, const int next[]) {
    int i = 1;  // 主串当前位置
    int j = 1;  // 子串当前位置

    while (i <= str->length && j <= subStr->length) {
        //主串不动 子串动
        if (j == 0 || str->str[i] == subStr->str[j]) {
            ++i;
            ++j;
        } else {
            j = next[j];
        }
    }

    if (j > subStr->length) {
        return i - subStr->length;  // 匹配成功，返回起始位置
    }

    return 0;  // 匹配失败
}

全部代码

stringKMP.h

c 复制代码 
#include<stdio.h>
#include<stdlib.h>

typedef struct {
	char* s;
	int len;
}strType;


void initStr(strType* str);

void CopyStr(strType* str,const char* s);

int simple_index(strType* str, strType* substr);

int KMPIndex(strType* str, strType* substr);

void releaseStr(strType* str);

KMP和暴力

c 复制代码 
#include"stringKMP.h"

void initStr(strType* str) {
	str->len = 0;
	str->s = NULL;
}

void CopyStr(strType* str, const char* s) {
	if (str->s) {
		free(str->s);
		str->s = NULL;
	}

	int len = 0;//分配多少空间
	while (s[len]) {
		len++;
	}

	//0位置不放字符以及'\0'
	str->s = malloc(sizeof(strType) * (len + 2));
	if (str->s == NULL)return;
	str->len = len;

	//赋值
	for (int i = 0; i <= len; i++)
	{
		//str->s[i + 1] [1,len+1]
		//s[i] [0,len]
		str->s[i + 1] = s[i];
	}
	
	//检验copy成功
	printf("\n=======\n");
	for (int i = 0; i <= len; i++)
	{
		
		printf("%c", str->s[i + 1]);
	}
	printf("\n=======\n");

}

int simple_index(strType* str, strType* substr) {

	int i = 1;//主串索引
	int j = 1;//模式串索引
	int k = i;//记录主串回溯位置 模式串回溯到开头

	while (i <= str->len && j <= substr->len) {
		if (str->s[i] == substr->s[j]) {
			++i;
			++j;
			k = i;
		}
		else {
			k++;//主串移动一个位置匹配
			i = k;
			j = 1;
		}
	}
	//循环结束模式串走到了末尾 证明是子串
	if (j > substr->len) {
		return i - substr->len;
	}

	return 0;
}

//回溯数组next[i]
//next[i]=[1,i-1]里面的公共前后缀个数+1
static void getnext(strType* substr, int next[]) {
	next[0] = 0;//不装东西
	next[1] = 0;

	int cur = 1;//当前模式串索引
	int k = 0;//next值

	 
	while (cur < substr->len) {
		if (k == 0) {
			++cur;
			++k;//索引2 只有一个
			//没有公共前后缀（而且不是本身 ） next[2]=0+1
			next[cur] = k;
		}

		if (substr->s[cur] == substr->s[k]) {
			++cur;
			++k;
			next[cur] = k;
		}
		else {
			k = next[k];
		}
	}

	/*for (int i = 1; i <= cur; i++)
	{
		printf("%d ", next[i]);
	}*/
}

//主串不回溯 模式串回溯
// 回溯数组next 模式串i位置不匹配时回溯的位置为next[i]
int KMPIndex(strType* str, strType* substr) {
	int i = 1;//主串索引
	int j = 1;//模式串索引而且和next数组值有关

	//空出第一位
	int* next = malloc(sizeof(int) * (str->len+1));
	if (next == NULL)return -1;
	getnext(substr, next);
	
	
	while (i <= str->len && j <= substr->len) {
		if (j==0||str->s[i] == substr->s[j]) {
			i++;
			j++;
			
		}
		else {
			j = next[j];
		}
	}

	if (j > substr->len) {
		return i - substr->len;
	}

	return 0;
}


void releaseStr(strType* str) {
	if (str->s) {
		free(str->s);
		str->s = NULL;
	}
}

void test01() {
	strType str;
	strType substr;
	initStr(&str);
	initStr(&substr);

	CopyStr(&str, "ABCDABCABCABABCABCD");
	CopyStr(&substr, "ABCABCD");//abaaabagabaaabaa

	/*int res = simple_index(&str, &substr);
	printf("simple_index:%d\n", res);*/

	int res=KMPIndex(&str, &substr);
	printf("KMPIndex:%d\n", res);
}

int main() {

	test01();
	return 0;
}
/*ABCDABCABCABABCABCD
  ABCABCD
*/
相关推荐
整得咔咔响3 小时前
贝尔曼最优公式(BOE)
人工智能·算法·机器学习
renke33643 小时前
Flutter for OpenHarmony：数字涟漪 - 基于扩散算法的逻辑解谜游戏设计与实现
算法·flutter·游戏
AI科技星3 小时前
从ZUFT光速螺旋运动求导推出自然常数e
服务器·人工智能·线性代数·算法·矩阵
老鼠只爱大米3 小时前
LeetCode经典算法面试题 #78：子集（回溯法、迭代法、动态规划等多种实现方案详细解析）
算法·leetcode·动态规划·回溯·位运算·子集
执着2593 小时前
力扣hot100 - 199、二叉树的右视图
数据结构·算法·leetcode
I_LPL4 小时前
day21 代码随想录算法训练营 二叉树专题8
算法·二叉树·递归
可编程芯片开发4 小时前
基于PSO粒子群优化PI控制器的无刷直流电机最优控制系统simulink建模与仿真
人工智能·算法·simulink·pso·pi控制器·pso-pi
cpp_25014 小时前
P8448 [LSOT-1] 暴龙的土豆
数据结构·c++·算法·题解·洛谷
lcj25114 小时前
深入理解指针（4）：qsort 函数 & 通过冒泡排序实现
c语言·数据结构·算法
热门推荐
01GitHub 镜像站点02Claude Code + GLM4.7 避坑指南：解决 Unable to connect to Anthropic services03UV安装并设置国内源04openclaw配置教程（linux+局域网ollama）05Linux下V2Ray安装配置指南06OpenClaw Chrome扩展使用教程 - 浏览器中继控制07AI 规范驱动开发“三剑客”深度对比：Spec-Kit、Kiro 与 OpenSpec 实战指南08Claude Code Skills 实用使用手册09openclaw使用nginx反代部署过程 与disconnected (1008): pairing required解决10Vue-skills的中文文档