《数字图像处理》第 4 章 - 频域滤波

啊阿狸不会拉杆2026-01-18 20:25

前言

频域滤波是数字图像处理的核心技术之一，其核心思想是将图像从空间域转换到频率域，通过修改频率分量实现图像增强、去噪、锐化等操作。本文将按照《数字图像处理》第 4 章的完整目录，用通俗易懂的语言讲解频域滤波的全知识点，并配套可直接运行的 Python 代码、效果对比图，帮你彻底吃透频域滤波！

4.1 背景知识

4.1.1 傅里叶级数与傅里叶变换的发展简史

傅里叶变换的核心是 "任何周期函数都可以分解为正弦 / 余弦函数的叠加"，其发展脉络可总结为：

  • 1807 年，傅里叶提出 "任何周期函数都可展开为三角函数级数"（傅里叶级数）；
  • 1822 年，《热的解析理论》正式发表，奠定傅里叶分析基础；
  • 后续经柯西、狄利克雷等数学家完善，形成现代傅里叶变换体系；
  • 数字时代，离散傅里叶变换（DFT）和快速傅里叶变换（FFT）让傅里叶分析落地到计算机图像处理。

4.1.2 本章示例说明

本章所有示例基于 Python 实现，依赖库包括：numpy（数值计算）、cv2（图像读取 / 处理）、matplotlib（可视化）、scipy（信号处理）。环境准备：

复制代码 
pip install numpy opencv-python matplotlib scipy

4.2 预备知识

4.2.1 复数

代码示例：复数基本运算

python 复制代码 
import numpy as np

# 定义复数（三种正确方式，任选其一即可）
# 方式1：直接用Python原生复数（推荐，最简单）
z1 = 3 + 4j  # 3+4j
z2 = 1 + 2j  # 1+2j

# 方式2：np.complex_ 传入字符串（兼容旧版本NumPy）
# z1 = np.complex_("3+4j")
# z2 = np.complex_("1+2j")

# 方式3：np.array 构造复数数组（适合批量定义）
# z1 = np.array([3, 4], dtype=np.complex128)
# z2 = np.array([1, 2], dtype=np.complex128)

# 基本运算
z_add = z1 + z2       # 加法
z_mul = z1 * z2       # 乘法
z_abs = np.abs(z1)    # 模长
z_angle = np.angle(z1)# 辐角（弧度）

# 输出结果
print(f"z1 = {z1}, z2 = {z2}")
print(f"z1 + z2 = {z_add}")
print(f"z1 * z2 = {z_mul}")
print(f"|z1| = {z_abs}, 辐角 = {z_angle:.2f} rad")

输出：

复制代码 
z1 = (3+4j), z2 = (1+2j)
z1 + z2 = (4+6j)
z1 * z2 = (-5+10j)
|z1| = 5.0, 辐角 = 0.93 rad

4.2.2 傅里叶级数

代码示例：方波的傅里叶级数逼近

复制代码 
import numpy as np
import matplotlib.pyplot as plt

# 设置中文字体（解决matplotlib中文显示问题）
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False

# 定义方波函数
def square_wave(t, T=2*np.pi):
    return np.where(np.mod(t, T) < T/2, 1, -1)

# 傅里叶级数逼近
def fourier_series(t, n_max, T=2*np.pi):
    omega0 = 2*np.pi / T
    result = 0
    for n in range(1, n_max+1, 2):  # 只保留奇次谐波
        an = 0
        bn = 4/(n*np.pi)
        result += an*np.cos(n*omega0*t) + bn*np.sin(n*omega0*t)
    return result

# 生成数据
t = np.linspace(-2*np.pi, 2*np.pi, 1000)
y_original = square_wave(t)

# 不同项数的逼近
y_1 = fourier_series(t, 1)
y_5 = fourier_series(t, 5)
y_20 = fourier_series(t, 20)

# 可视化对比
plt.figure(figsize=(12, 8))
plt.subplot(2, 2, 1)
plt.plot(t, y_original, label='原始方波')
plt.title('原始方波')
plt.grid(True)

plt.subplot(2, 2, 2)
plt.plot(t, y_1, label='1项逼近', color='orange')
plt.title('1项傅里叶级数逼近')
plt.grid(True)

plt.subplot(2, 2, 3)
plt.plot(t, y_5, label='5项逼近', color='red')
plt.title('5项傅里叶级数逼近')
plt.grid(True)

plt.subplot(2, 2, 4)
plt.plot(t, y_20, label='20项逼近', color='green')
plt.title('20项傅里叶级数逼近')
plt.grid(True)

plt.tight_layout()
plt.show()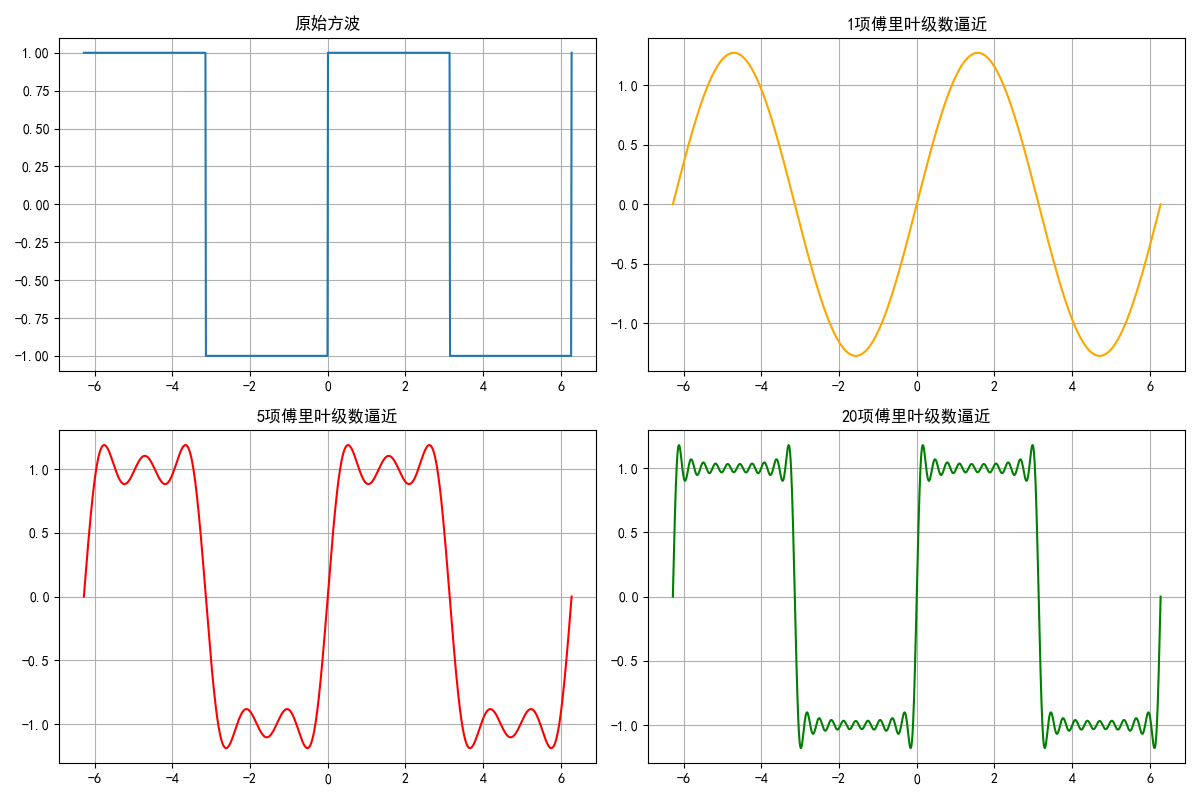

效果对比图：

  • 1 项逼近：仅一条正弦曲线，与方波差距大；
  • 5 项逼近：开始接近方波轮廓；
  • 20 项逼近：几乎与原始方波重合，验证了 "傅里叶级数可逼近周期函数"。

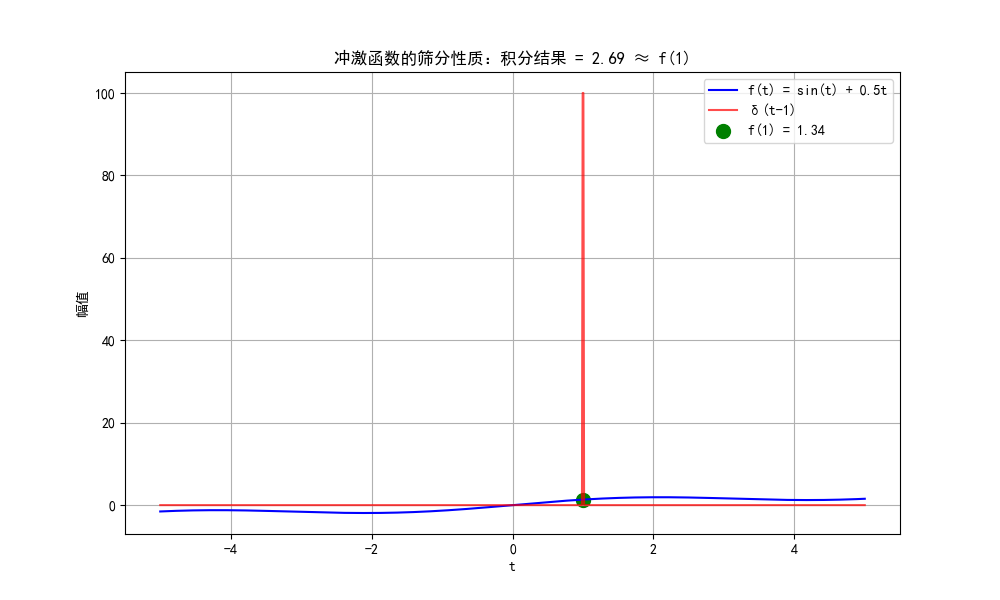
4.2.3 冲激函数及其筛分性质

代码示例：冲激函数可视化与筛分性质验证

复制代码 
import numpy as np
import matplotlib.pyplot as plt

plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False

# 模拟冲激函数（离散近似）
def delta_func(t, t0=0, eps=0.01):
    return np.where(np.abs(t - t0) < eps, 1/eps, 0)

# 定义测试函数
def f(t):
    return np.sin(t) + 0.5*t

# 生成数据
t = np.linspace(-5, 5, 1000)
delta = delta_func(t, t0=1)  # t0=1处的冲激
f_t = f(t)

# 验证筛分性质：积分f(t)*delta(t-1) ≈ f(1)
integral = np.trapz(f_t * delta, t)
f_1 = f(1)

# 可视化
plt.figure(figsize=(10, 6))
plt.plot(t, f_t, label='f(t) = sin(t) + 0.5t', color='blue')
plt.plot(t, delta, label='δ(t-1)', color='red', alpha=0.7)
plt.scatter(1, f_1, color='green', s=100, label=f'f(1) = {f_1:.2f}')
plt.title(f'冲激函数的筛分性质：积分结果 = {integral:.2f} ≈ f(1)')
plt.xlabel('t')
plt.ylabel('幅值')
plt.legend()
plt.grid(True)
plt.show()

4.2.4 单变量连续函数的傅里叶变换

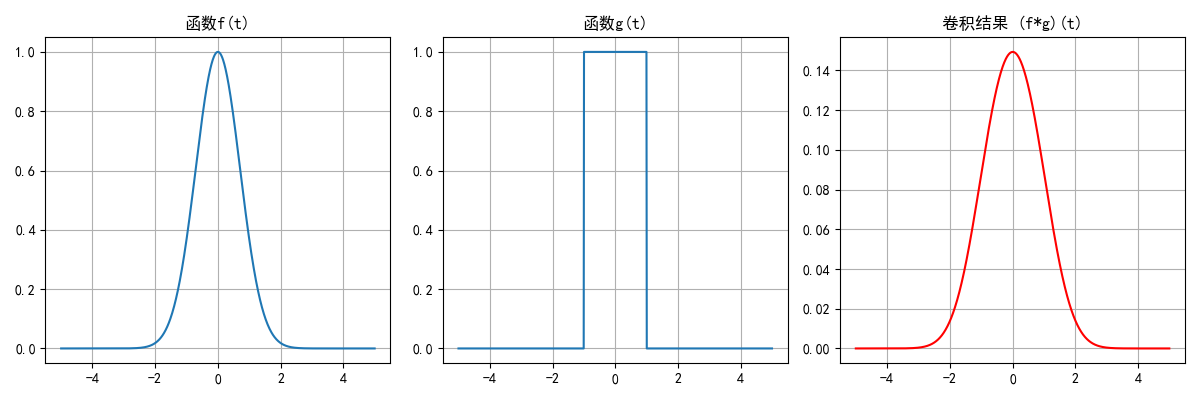
4.2.5 卷积

代码示例：卷积可视化

复制代码 
import numpy as np
import matplotlib.pyplot as plt
from scipy.signal import convolve

plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False

# 定义两个函数
t = np.linspace(-5, 5, 1000)
f = np.exp(-t**2)  # 高斯函数
g = np.where((t >= -1) & (t <= 1), 1, 0)  # 矩形窗

# 计算卷积
conv = convolve(f, g, mode='same') / len(t)  # 归一化

# 可视化
plt.figure(figsize=(12, 4))
plt.subplot(1, 3, 1)
plt.plot(t, f, label='f(t) = e^(-t²)')
plt.title('函数f(t)')
plt.grid(True)

plt.subplot(1, 3, 2)
plt.plot(t, g, label='g(t) 矩形窗')
plt.title('函数g(t)')
plt.grid(True)

plt.subplot(1, 3, 3)
plt.plot(t, conv, label='f*g', color='red')
plt.title('卷积结果 (f*g)(t)')
plt.grid(True)

plt.tight_layout()
plt.show()

4.3 采样与采样函数的傅里叶变换

4.3.1 采样原理

4.3.2 采样函数的傅里叶变换

4.3.3 采样定理

4.3.4 混叠现象

当采样频率不满足奈奎斯特定理时，高频分量会 "折叠" 到低频区域，导致信号失真，称为混叠。

代码示例：采样与混叠对比

复制代码 
import numpy as np
import matplotlib.pyplot as plt

plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False

# 定义原始信号：10Hz + 20Hz 正弦波
def signal(t):
    return np.sin(2*np.pi*10*t) + 0.5*np.sin(2*np.pi*20*t)

# 生成连续信号
t_continuous = np.linspace(0, 1, 1000)
y_continuous = signal(t_continuous)

# 采样1：满足奈奎斯特（采样频率50Hz > 2*20Hz）
fs1 = 50
t1 = np.linspace(0, 1, fs1)
y1 = signal(t1)

# 采样2：不满足奈奎斯特（采样频率30Hz < 2*20Hz）
fs2 = 30
t2 = np.linspace(0, 1, fs2)
y2 = signal(t2)

# 可视化
plt.figure(figsize=(12, 8))
plt.subplot(2, 1, 1)
plt.plot(t_continuous, y_continuous, label='原始连续信号', color='blue')
plt.scatter(t1, y1, color='red', label=f'采样频率{fs1}Hz（无混叠）')
plt.title('满足奈奎斯特定理：无混叠')
plt.xlabel('时间 (s)')
plt.ylabel('幅值')
plt.legend()
plt.grid(True)

plt.subplot(2, 1, 2)
plt.plot(t_continuous, y_continuous, label='原始连续信号', color='blue')
plt.scatter(t2, y2, color='orange', label=f'采样频率{fs2}Hz（混叠）')
plt.title('不满足奈奎斯特定理：混叠失真')
plt.xlabel('时间 (s)')
plt.ylabel('幅值')
plt.legend()
plt.grid(True)

plt.tight_layout()
plt.show()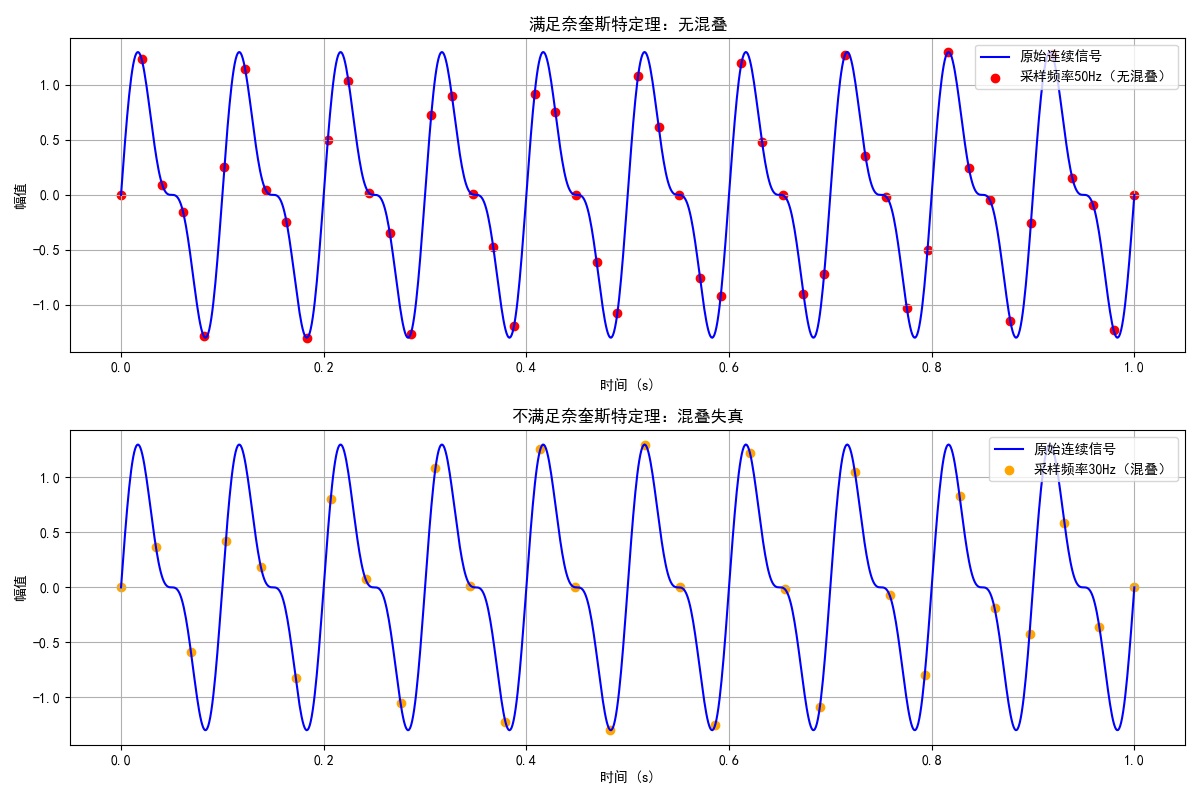

效果对比：

  • 50Hz 采样：离散点能准确还原原始信号；
  • 30Hz 采样：离散点明显偏离原始信号，出现混叠失真。

4.3.5 基于采样数据的函数重建（恢复）

4.4 单变量离散傅里叶变换（DFT）

4.4.1 由采样函数的连续傅里叶变换推导离散傅里叶变换

4.4.2 采样间隔与频率间隔的关系

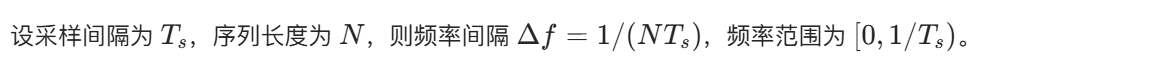
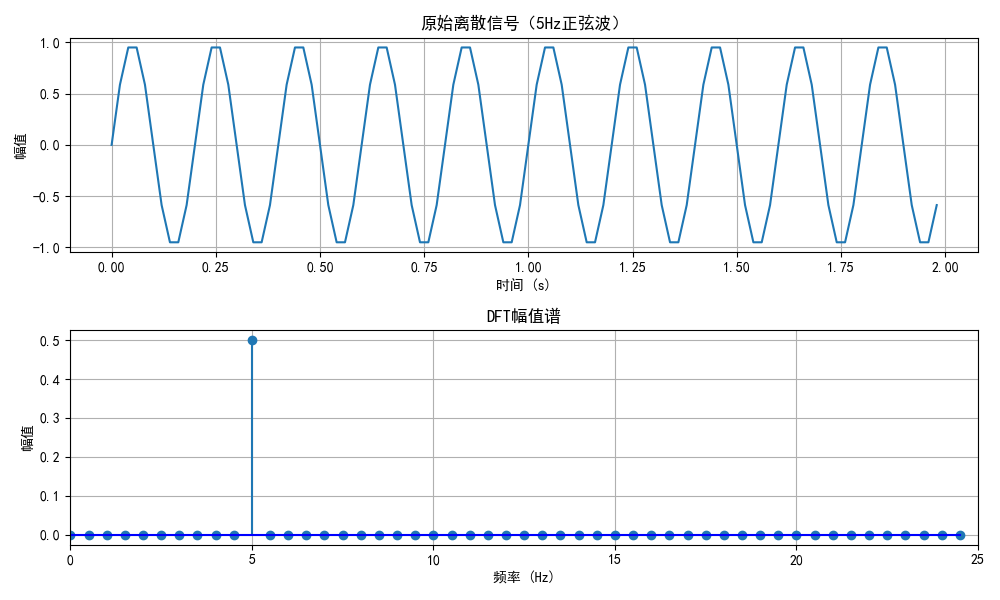
代码示例：单变量 DFT 计算

复制代码 
import numpy as np
import matplotlib.pyplot as plt

plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False

# 生成离散信号：5Hz正弦波，采样频率50Hz，长度100
fs = 50
N = 100
t = np.arange(N) / fs
f_n = np.sin(2*np.pi*5*t)

# 计算DFT
F_k = np.fft.fft(f_n)
# 频率轴
freq = np.fft.fftfreq(N, 1/fs)
# 幅值谱（归一化）
amp = np.abs(F_k) / N

# 可视化
plt.figure(figsize=(10, 6))
plt.subplot(2, 1, 1)
plt.plot(t, f_n)
plt.title('原始离散信号（5Hz正弦波）')
plt.xlabel('时间 (s)')
plt.ylabel('幅值')
plt.grid(True)

plt.subplot(2, 1, 2)
plt.stem(freq, amp, basefmt='b-')
plt.title('DFT幅值谱')
plt.xlabel('频率 (Hz)')
plt.ylabel('幅值')
plt.xlim(0, fs/2)  # 只显示正频率
plt.grid(True)

plt.tight_layout()
plt.show()

4.5 扩展至双变量函数

4.5.1 二维冲激函数及其筛分性质

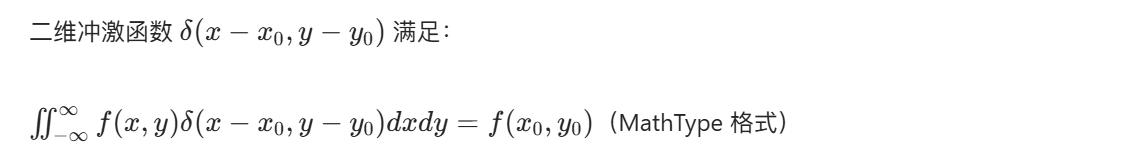
4.5.2 二维连续傅里叶变换对

4.5.3 二维采样与二维采样定理

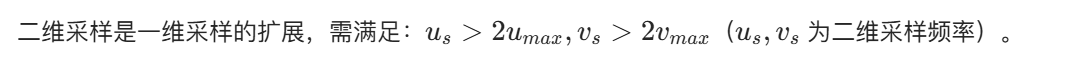
4.5.4 图像中的混叠现象

图像采样时，若分辨率不足（采样频率低），会出现边缘模糊、摩尔纹等混叠现象（如低分辨率图片放大后的锯齿）。

4.5.5 二维离散傅里叶变换及其逆变换

代码示例：图像的二维 DFT 与逆变换

复制代码 
import numpy as np
import cv2
import matplotlib.pyplot as plt

plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False

# 读取图像（灰度图）
img = cv2.imread('lena.jpg', cv2.IMREAD_GRAYSCALE)
if img is None:
    # 若读取失败，生成测试图像
    img = np.zeros((256, 256), dtype=np.uint8)
    img[100:150, 100:150] = 255  # 白色方块

# 计算二维DFT
dft = np.fft.fft2(img)
# 将低频移到中心
dft_shift = np.fft.fftshift(dft)
# 幅值谱（对数缩放，便于可视化）
magnitude_spectrum = 20 * np.log(np.abs(dft_shift))

# 逆DFT
dft_shift_back = np.fft.ifftshift(dft_shift)
img_back = np.fft.ifft2(dft_shift_back)
img_back = np.abs(img_back).astype(np.uint8)

# 可视化
plt.figure(figsize=(12, 6))
plt.subplot(1, 3, 1)
plt.imshow(img, cmap='gray')
plt.title('原始图像')
plt.axis('off')

plt.subplot(1, 3, 2)
plt.imshow(magnitude_spectrum, cmap='gray')
plt.title('DFT幅值谱（中心对齐）')
plt.axis('off')

plt.subplot(1, 3, 3)
plt.imshow(img_back, cmap='gray')
plt.title('逆DFT恢复图像')
plt.axis('off')

plt.tight_layout()
plt.show()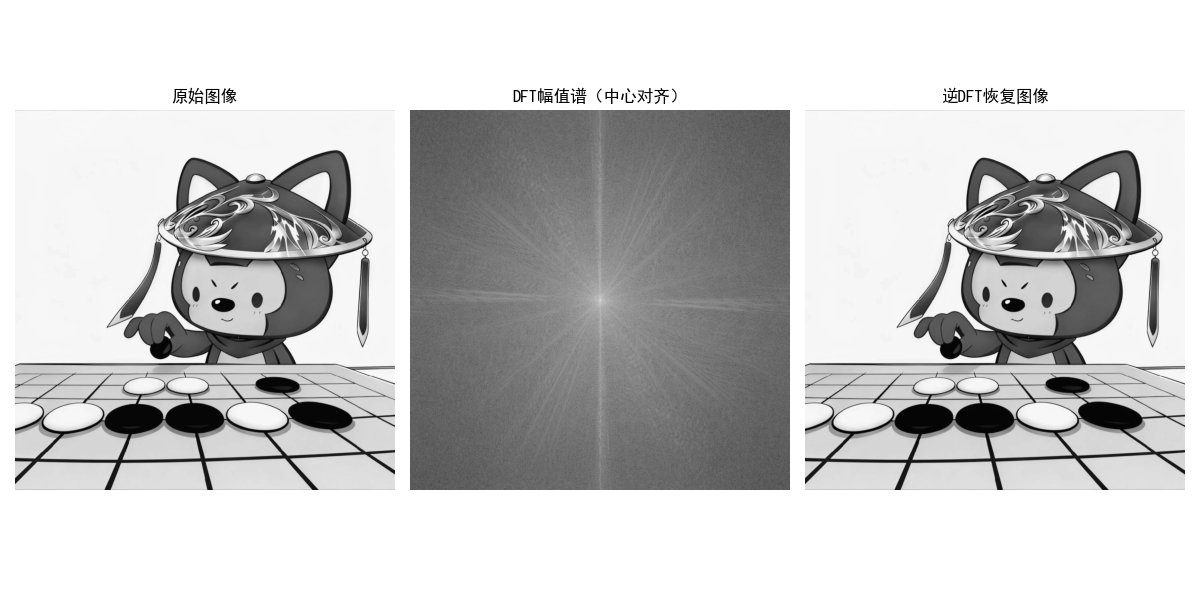

效果说明：

  • 原始图像：灰度图（或测试方块图）；
  • 幅值谱：中心亮斑为低频分量（对应图像整体亮度），边缘为高频分量（对应边缘 / 细节）；
  • 恢复图像：与原始图像几乎一致，验证 IDFT 的正确性。

4.6 二维离散傅里叶变换的性质

4.6.1 空间域间隔与频域间隔的关系

4.6.2 平移性与旋转性

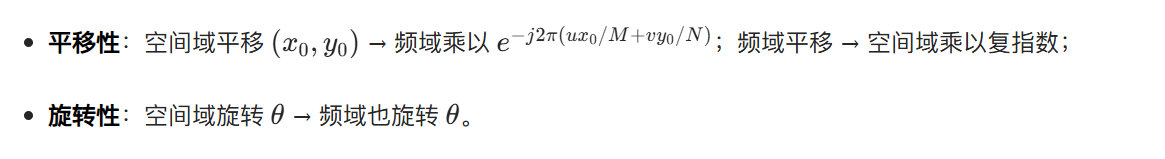
代码示例：图像平移的 DFT 变化

复制代码 
import numpy as np
import cv2
import matplotlib.pyplot as plt

plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False

# 读取图像
img = cv2.imread('lena.jpg', cv2.IMREAD_GRAYSCALE)
if img is None:
    img = np.zeros((256, 256), dtype=np.uint8)
    img[100:150, 100:150] = 255

# 图像平移（右移50，下移50）
M, N = img.shape
dx, dy = 50, 50
img_shift = np.roll(np.roll(img, dx, axis=1), dy, axis=0)

# 计算DFT
dft_original = np.fft.fftshift(np.fft.fft2(img))
dft_shift = np.fft.fftshift(np.fft.fft2(img_shift))

# 幅值谱
mag_original = 20 * np.log(np.abs(dft_original))
mag_shift = 20 * np.log(np.abs(dft_shift))

# 可视化
plt.figure(figsize=(12, 6))
plt.subplot(2, 2, 1)
plt.imshow(img, cmap='gray')
plt.title('原始图像')
plt.axis('off')

plt.subplot(2, 2, 2)
plt.imshow(img_shift, cmap='gray')
plt.title('平移后图像')
plt.axis('off')

plt.subplot(2, 2, 3)
plt.imshow(mag_original, cmap='gray')
plt.title('原始图像DFT幅值谱')
plt.axis('off')

plt.subplot(2, 2, 4)
plt.imshow(mag_shift, cmap='gray')
plt.title('平移图像DFT幅值谱')
plt.axis('off')

plt.tight_layout()
plt.show()

效果说明：平移后图像的 DFT 幅值谱与原始一致（仅相位变化），验证平移性。

4.6.3 周期性

4.6.4 对称性

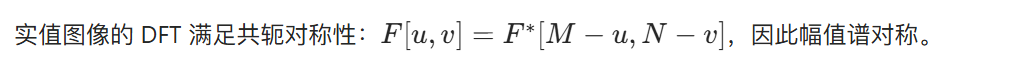
4.6.5 傅里叶谱与相位角

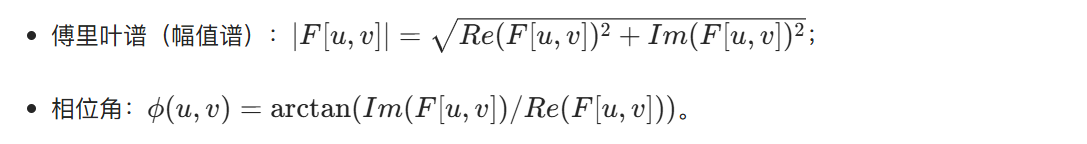
代码示例：幅值谱与相位谱可视化

复制代码 
import numpy as np
import cv2
import matplotlib.pyplot as plt

plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False

img = cv2.imread('lena.jpg', cv2.IMREAD_GRAYSCALE)
if img is None:
    img = np.zeros((256, 256), dtype=np.uint8)
    img[100:150, 100:150] = 255

# 计算DFT并移到中心
dft = np.fft.fft2(img)
dft_shift = np.fft.fftshift(dft)

# 幅值谱和相位谱
magnitude = 20 * np.log(np.abs(dft_shift))
phase = np.angle(dft_shift)

# 可视化
plt.figure(figsize=(12, 6))
plt.subplot(1, 3, 1)
plt.imshow(img, cmap='gray')
plt.title('原始图像')
plt.axis('off')

plt.subplot(1, 3, 2)
plt.imshow(magnitude, cmap='gray')
plt.title('幅值谱')
plt.axis('off')

plt.subplot(1, 3, 3)
plt.imshow(phase, cmap='gray')
plt.title('相位谱')
plt.axis('off')

plt.tight_layout()
plt.show()

4.6.6 二维卷积定理

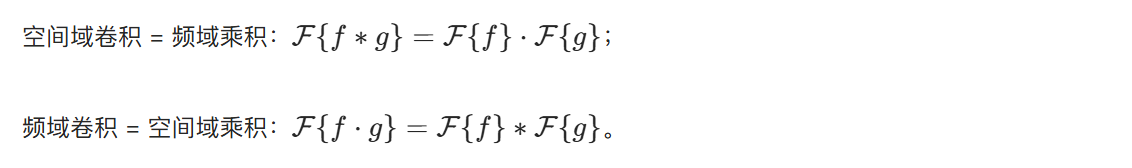
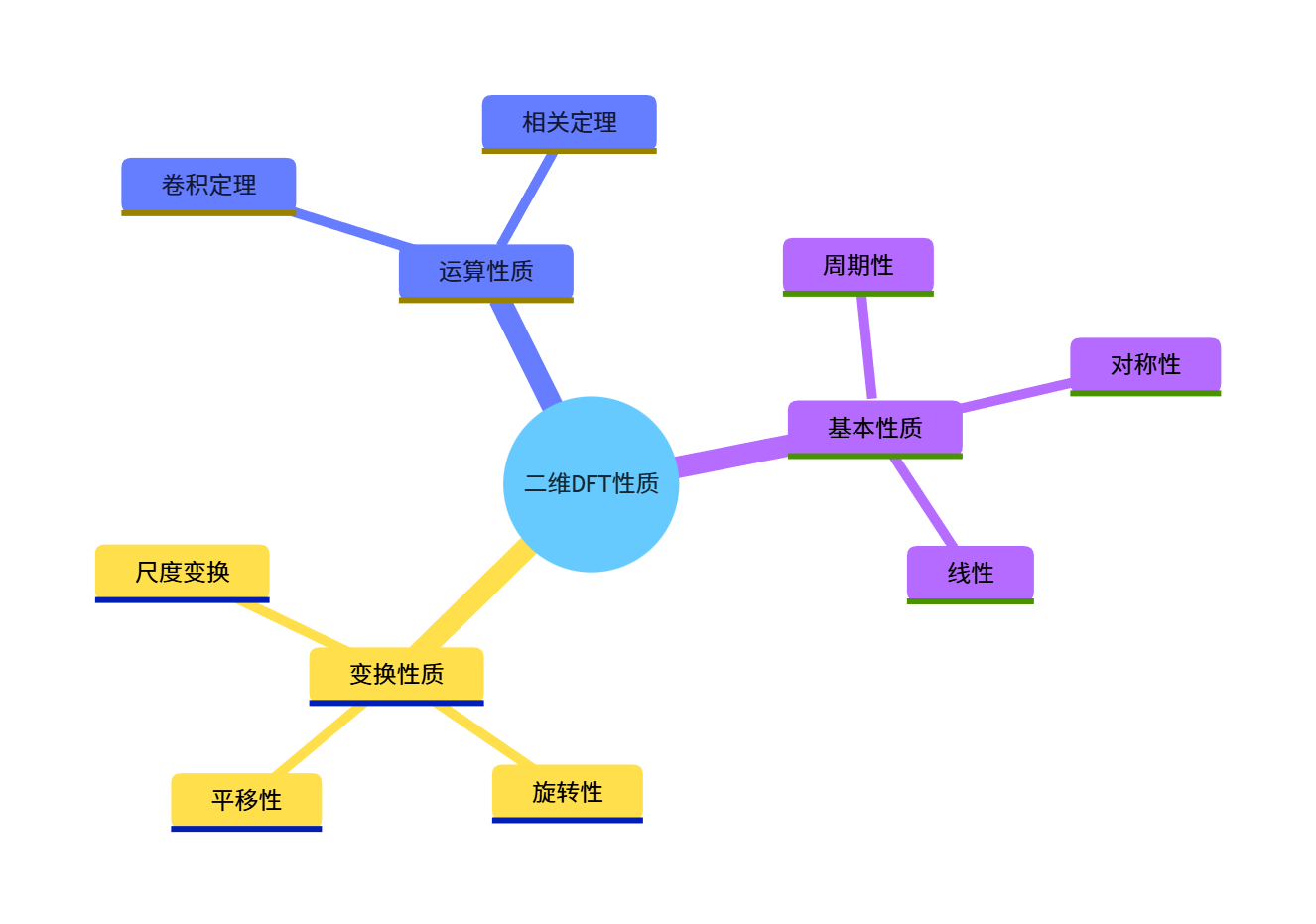
4.6.7 二维离散傅里叶变换性质总结

4.7 频域滤波基础

4.7.1 频域的其他特性

  • 低频分量：对应图像的整体亮度、大结构；
  • 高频分量：对应图像的边缘、细节、噪声；
  • 滤波核心：修改频域分量（保留 / 增强 / 抑制），再逆变换回空间域。

4.7.2 频域滤波基本原理

4.7.3 频域滤波步骤总结

  1. 图像预处理：灰度化、补零（可选）；
  2. 计算二维 DFT 并中心对齐；
  3. 设计频域滤波器（低通 / 高通 / 带通等）；
  4. 频域相乘（滤波）；
  5. 逆 DFT 转换回空间域；
  6. 后处理：归一化、取实部。

4.7.4 空间域滤波与频域滤波的对应关系

空间域操作 频域操作
平滑（均值 / 高斯滤波） 低通滤波
锐化（拉普拉斯 / Sobel） 高通滤波
边缘检测 高通滤波
噪声去除 低通滤波

4.8 基于频域滤波器的图像平滑

图像平滑的核心是抑制高频分量（噪声 / 细节），保留低频分量。

4.8.1 理想低通滤波器（ILPF）

4.8.2 巴特沃斯低通滤波器（BLPF）

4.8.3 高斯低通滤波器（GLPF）

4.8.4 低通滤波的扩展示例

完整代码：三种低通滤波器对比

python 复制代码 
import numpy as np
import cv2
import matplotlib.pyplot as plt

plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False

# 1. 读取并预处理图像
img = cv2.imread('../picture/AALi.jpg', cv2.IMREAD_GRAYSCALE)
if img is None:
    # 生成测试图像（添加噪声）
    img = np.zeros((256, 256), dtype=np.uint8)
    img[80:180, 80:180] = 255
    # 添加高斯噪声
    noise = np.random.normal(0, 30, img.shape).astype(np.float32)
    img = np.clip(img + noise, 0, 255).astype(np.uint8)

M, N = img.shape  # M=高度(行), N=宽度(列)
print(f"图像形状：M={M}, N={N}")  # 打印维度，方便排查

# 2. 计算DFT并中心对齐
dft = np.fft.fft2(img)
dft_shift = np.fft.fftshift(dft)

# 3. 生成频域网格（关键修正：先v后u，匹配图像行列）
# 注意：meshgrid第一个参数对应列(v)，第二个对应行(u)
v = np.arange(N)  # 列方向（宽度）
u = np.arange(M)  # 行方向（高度）
u_grid, v_grid = np.meshgrid(u, v, indexing='ij')  # indexing='ij' 确保(u,v)对应(行,列)

# 中心坐标
u0, v0 = M // 2, N // 2
# 距离D(u,v)：计算每个频域点到中心的欧式距离
D = np.sqrt((u_grid - u0) ** 2 + (v_grid - v0) ** 2)
print(f"距离矩阵形状：{D.shape}，DFT移位后形状：{dft_shift.shape}")  # 验证维度匹配

# 4. 设计滤波器（截止频率D0=30）
D0 = 30
n = 2  # 巴特沃斯阶数

# 理想低通
H_ilpf = np.where(D <= D0, 1, 0)
# 巴特沃斯低通
H_blpf = 1 / (1 + (D / D0) ** (2 * n))
# 高斯低通
H_glpf = np.exp(-(D ** 2) / (2 * D0 ** 2))

# 5. 频域滤波（现在维度匹配，可正常相乘）
g_shift_ilpf = dft_shift * H_ilpf
g_shift_blpf = dft_shift * H_blpf
g_shift_glpf = dft_shift * H_glpf

# 6. 逆DFT（添加小技巧：取实部后归一化，避免数值误差）
# 理想低通
g_ilpf = np.fft.ifftshift(g_shift_ilpf)
g_ilpf = np.fft.ifft2(g_ilpf)
g_ilpf = np.real(g_ilpf)  # 优先取实部，避免虚部残留
g_ilpf = np.clip(g_ilpf, 0, 255).astype(np.uint8)  # 归一化到0-255

# 巴特沃斯低通
g_blpf = np.fft.ifftshift(g_shift_blpf)
g_blpf = np.fft.ifft2(g_blpf)
g_blpf = np.real(g_blpf)
g_blpf = np.clip(g_blpf, 0, 255).astype(np.uint8)

# 高斯低通
g_glpf = np.fft.ifftshift(g_shift_glpf)
g_glpf = np.fft.ifft2(g_glpf)
g_glpf = np.real(g_glpf)
g_glpf = np.clip(g_glpf, 0, 255).astype(np.uint8)

# 7. 可视化（补充第8个子图，避免布局警告）
plt.figure(figsize=(15, 10))
# 原始图像
plt.subplot(2, 4, 1)
plt.imshow(img, cmap='gray')
plt.title('原始图像（含噪声）')
plt.axis('off')
# 理想低通
plt.subplot(2, 4, 2)
plt.imshow(g_ilpf, cmap='gray')
plt.title('理想低通滤波（振铃效应明显）')
plt.axis('off')
# 巴特沃斯低通
plt.subplot(2, 4, 3)
plt.imshow(g_blpf, cmap='gray')
plt.title('巴特沃斯低通（轻微振铃）')
plt.axis('off')
# 高斯低通
plt.subplot(2, 4, 4)
plt.imshow(g_glpf, cmap='gray')
plt.title('高斯低通（无振铃）')
plt.axis('off')

# 滤波器可视化
plt.subplot(2, 4, 5)
plt.imshow(H_ilpf, cmap='gray')
plt.title('理想低通滤波器')
plt.axis('off')
plt.subplot(2, 4, 6)
plt.imshow(H_blpf, cmap='gray')
plt.title('巴特沃斯低通滤波器')
plt.axis('off')
plt.subplot(2, 4, 7)
plt.imshow(H_glpf, cmap='gray')
plt.title('高斯低通滤波器')
plt.axis('off')
# 补充第8个子图（避免布局警告）
plt.subplot(2, 4, 8)
plt.text(0.5, 0.5, '低通滤波对比', ha='center', va='center', fontsize=12)
plt.axis('off')

plt.tight_layout()
plt.show()

效果对比：

  • 理想低通：噪声去除明显，但边缘出现振铃效应（吉布斯现象）；
  • 巴特沃斯低通：振铃效应减轻，平滑效果适中；
  • 高斯低通：无振铃效应，平滑效果最自然。

4.9 基于频域滤波器的图像锐化

图像锐化的核心是增强高频分量（边缘 / 细节），抑制低频分量。

4.9.1 理想高通滤波器（IHPF）

4.9.2 巴特沃斯高通滤波器（BHPF）

4.9.3 高斯高通滤波器（GHPF）

4.9.4 频域中的拉普拉斯算子

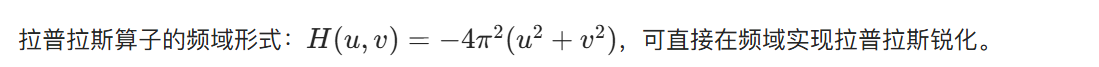
4.9.5 非锐化掩模、高提升滤波与高频强调滤波

4.9.6 同态滤波

同时增强对比度和抑制噪声，核心是将图像分解为照度（低频）和反射（高频）分量：

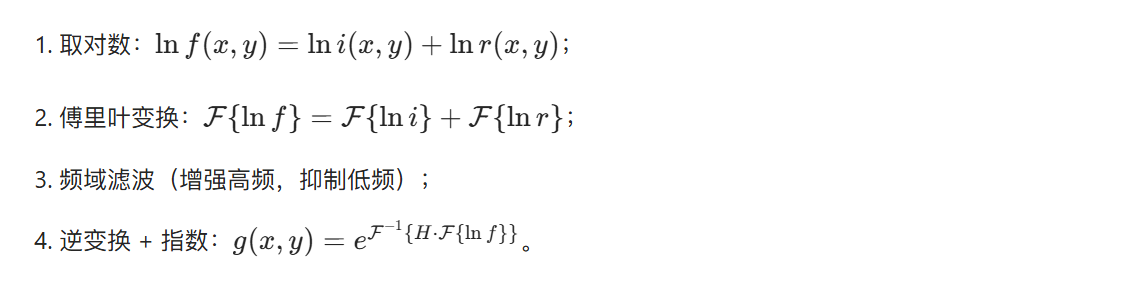
完整代码：高通滤波 + 同态滤波对比

python 复制代码 
import numpy as np
import cv2
import matplotlib.pyplot as plt

plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False

# 1. 读取图像
img = cv2.imread('../picture/TianHuoSanXuanBian.jpg', cv2.IMREAD_GRAYSCALE)
if img is None:
    # 生成测试图像（低对比度）
    img = np.zeros((256, 256), dtype=np.uint8)
    img[80:180, 80:180] = 255
    # 降低对比度
    img = (img * 0.5).astype(np.uint8)

M, N = img.shape  # M=高度(行), N=宽度(列)
print(f"图像形状：M={M}, N={N}")  # 打印维度，方便排查

# 2. 计算DFT并中心对齐
dft = np.fft.fft2(img.astype(np.float32))
dft_shift = np.fft.fftshift(dft)

# 3. 生成频域网格（关键修正：匹配图像行列维度）
# 注意：先定义列(v)、后定义行(u)，并使用indexing='ij'确保维度匹配
v = np.arange(N)  # 列方向（宽度）
u = np.arange(M)  # 行方向（高度）
u_grid, v_grid = np.meshgrid(u, v, indexing='ij')  # 生成(M,N)形状的网格

# 中心坐标
u0, v0 = M // 2, N // 2
# 距离D(u,v)：添加极小值eps避免除零
eps = 1e-8  # 防止D=0导致除零
D = np.sqrt((u_grid - u0) ** 2 + (v_grid - v0) ** 2) + eps
print(f"距离矩阵形状：{D.shape}，DFT移位后形状：{dft_shift.shape}")  # 验证维度匹配

# 4. 设计高通滤波器（截止频率D0=30）
D0 = 30
n = 2    # 巴特沃斯阶数

# 理想高通
H_ihpf = np.where(D <= D0, 0, 1)

# 巴特沃斯高通（修正除零问题）
H_bhpf = 1 / (1 + (D0 / D) ** (2 * n))

# 高斯高通
H_ghpf = 1 - np.exp(-(D ** 2) / (2 * D0 ** 2))

# 高频强调滤波（加入直流分量，提升亮度）
H_hfe = 0.5 + 0.7 * H_ghpf

# 5. 同态滤波（增强对比度）
gamma_h = 2.0  # 高频增益（增强细节）
gamma_l = 0.5  # 低频增益（抑制背景）
c = 1
D1 = 30
H_homomorphic = (gamma_h - gamma_l) * (1 - np.exp(-c * (D ** 2) / (D1 ** 2))) + gamma_l

# 6. 滤波计算（统一优化：取实部+归一化，避免虚部误差）
# 理想高通
g_ihpf = np.fft.ifftshift(dft_shift * H_ihpf)
g_ihpf = np.fft.ifft2(g_ihpf)
g_ihpf = np.real(g_ihpf)  # 优先取实部，避免虚部残留
g_ihpf = np.clip(g_ihpf, 0, 255).astype(np.uint8)

# 巴特沃斯高通
g_bhpf = np.fft.ifftshift(dft_shift * H_bhpf)
g_bhpf = np.fft.ifft2(g_bhpf)
g_bhpf = np.real(g_bhpf)
g_bhpf = np.clip(g_bhpf, 0, 255).astype(np.uint8)

# 高频强调
g_hfe = np.fft.ifftshift(dft_shift * H_hfe)
g_hfe = np.fft.ifft2(g_hfe)
g_hfe = np.real(g_hfe)
g_hfe = np.clip(g_hfe, 0, 255).astype(np.uint8)

# 同态滤波（优化数值稳定性）
img_log = np.log1p(img.astype(np.float32))  # log(1+x)避免0值
dft_log = np.fft.fft2(img_log)
dft_log_shift = np.fft.fftshift(dft_log)
g_log_shift = dft_log_shift * H_homomorphic
g_log = np.fft.ifftshift(g_log_shift)
g_log = np.fft.ifft2(g_log)
g_homomorphic = np.expm1(np.real(g_log))  # exp(x)-1还原
g_homomorphic = np.clip(g_homomorphic, 0, 255).astype(np.uint8)

# 7. 可视化（补充第6个子图，避免布局警告）
plt.figure(figsize=(15, 10))
plt.subplot(2, 3, 1)
plt.imshow(img, cmap='gray')
plt.title('原始图像（低对比度）')
plt.axis('off')

plt.subplot(2, 3, 2)
plt.imshow(g_ihpf, cmap='gray')
plt.title('理想高通滤波（振铃+过暗）')
plt.axis('off')

plt.subplot(2, 3, 3)
plt.imshow(g_bhpf, cmap='gray')
plt.title('巴特沃斯高通滤波')
plt.axis('off')

plt.subplot(2, 3, 4)
plt.imshow(g_hfe, cmap='gray')
plt.title('高频强调滤波（亮度提升）')
plt.axis('off')

plt.subplot(2, 3, 5)
plt.imshow(g_homomorphic, cmap='gray')
plt.title('同态滤波（对比度增强）')
plt.axis('off')

# 补充第6个子图（显示滤波器示意图，提升实用性）
plt.subplot(2, 3, 6)
plt.imshow(H_hfe, cmap='gray')
plt.title('高频强调滤波器')
plt.axis('off')

plt.tight_layout()
plt.show()

效果对比：

  • 理想高通：边缘增强但有振铃，图像整体过暗；
  • 巴特沃斯高通：边缘增强，振铃减轻；
  • 高频强调：在增强边缘的同时提升整体亮度；
  • 同态滤波：同时增强对比度和细节，效果最优。

4.10 选择性滤波

4.10.1 带阻滤波器与带通滤波器

  • 带阻滤波器：抑制某一频段的分量（如去除特定频率的噪声）；
  • 带通滤波器：保留某一频段的分量（如提取特定频率的纹理）。

4.10.2 陷波滤波器

代码示例：陷波滤波器去除周期性噪声

python 复制代码 
import numpy as np
import cv2
import matplotlib.pyplot as plt

plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False

# 1. 读取/生成图像
img = cv2.imread('../picture/GaoDa.png', cv2.IMREAD_GRAYSCALE)
if img is None:
    # 备用测试图像（确保维度是行×列）
    img = np.ones((256, 256), dtype=np.uint8) * 128
    img[80:180, 80:180] = 255

# 核心：明确图像的行(M)和列(N)
M, N = img.shape  # M=高度(行), N=宽度(列)
print(f"✅ 图像形状（行×列）：{img.shape}")

# 2. 生成与图像完全匹配的网格（行×列 = M×N）
# 正确逻辑：先列(N)、后行(M)，indexing='xy' → 最终网格形状M×N
x = np.arange(N)  # 列坐标（0~N-1）
y = np.arange(M)  # 行坐标（0~M-1）
x_grid, y_grid = np.meshgrid(x, y, indexing='xy')  # 结果：x_grid(M×N), y_grid(M×N)
print(f"✅ 网格形状（行×列）：x_grid={x_grid.shape}, y_grid={y_grid.shape}")

# 3. 添加周期性噪声（维度100%匹配）
freq = 8  # 噪声频率（越大条纹越密）
noise_amp = 30  # 噪声幅值（越大条纹越明显）
# 生成与图像同维度的噪声
noise = noise_amp * (
    np.sin(2 * np.pi * freq * x_grid / N) +  # 水平条纹（沿列方向）
    np.sin(2 * np.pi * freq * y_grid / M)    # 垂直条纹（沿行方向）
)
print(f"✅ 噪声形状（行×列）：{noise.shape}")
# 叠加噪声并归一化
img_noisy = np.clip(img + noise, 0, 255).astype(np.uint8)

# 4. 计算DFT并中心化
dft = np.fft.fft2(img_noisy.astype(np.float32))
dft_shift = np.fft.fftshift(dft)
# 幅值谱（避免log(0)）
magnitude = 20 * np.log(np.abs(dft_shift) + 1e-8)

# 5. 设计陷波滤波器（精准抑制噪声频率）
# 频域中心
cy, cx = M // 2, N // 2
# 噪声频率对应的频域偏移（根据实际效果调整）
offset = freq
# 陷波中心（4个方向的噪声频率点）
notch_centers = [
    (cy, cx + offset), (cy, cx - offset),
    (cy + offset, cx), (cy - offset, cx)
]
print(f"✅ 陷波中心坐标：{notch_centers}")

# 巴特沃斯陷波滤波器参数
D0 = 15  # 陷波半径（大图像适当增大）
n = 4    # 阶数
eps = 1e-8  # 防除零

# 初始化全通滤波器
H_notch = np.ones((M, N), dtype=np.float32)
for (yc, xc) in notch_centers:
    # 计算每个点到陷波中心的距离
    D = np.sqrt((y_grid - yc)**2 + (x_grid - xc)**2) + eps
    # 陷波阻带（抑制该中心周围的频率）
    H_notch *= 1 / (1 + (D0 / D)**(2*n))

# 6. 频域滤波 + 逆变换
g_shift = dft_shift * H_notch
g = np.fft.ifftshift(g_shift)
g = np.fft.ifft2(g)
# 取实部并归一化（避免虚部残留）
g_filtered = np.clip(np.real(g), 0, 255).astype(np.uint8)

# 7. 可视化（清晰对比）
plt.figure(figsize=(18, 10))

# 原始图像
plt.subplot(2, 3, 1)
plt.imshow(img, cmap='gray')
plt.title('1. 原始无噪声图像', fontsize=12)
plt.axis('off')

# 含噪声图像
plt.subplot(2, 3, 2)
plt.imshow(img_noisy, cmap='gray')
plt.title('2. 含周期性条纹噪声的图像', fontsize=12)
plt.axis('off')

# DFT幅值谱
plt.subplot(2, 3, 3)
plt.imshow(magnitude, cmap='gray')
plt.title('3. 噪声图像DFT幅值谱\n（亮点=噪声频率）', fontsize=12)
plt.axis('off')

# 陷波滤波器
plt.subplot(2, 3, 4)
plt.imshow(H_notch, cmap='gray')
plt.title('4. 陷波滤波器\n（黑色=噪声抑制区）', fontsize=12)
plt.axis('off')

# 滤波后图像
plt.subplot(2, 3, 5)
plt.imshow(g_filtered, cmap='gray')
plt.title('5. 陷波滤波后图像\n（噪声已去除）', fontsize=12)
plt.axis('off')

# 噪声残留
plt.subplot(2, 3, 6)
residual = np.abs(img_noisy - g_filtered).astype(np.uint8)
plt.imshow(residual, cmap='gray')
plt.title('6. 噪声残留（越黑残留越少）', fontsize=12)
plt.axis('off')

plt.tight_layout()
plt.show()

4.11 实现方法

4.11.1 二维离散傅里叶变换的可分离性

4.11.2 利用离散傅里叶变换算法计算逆变换

4.11.3 快速傅里叶变换（FFT）

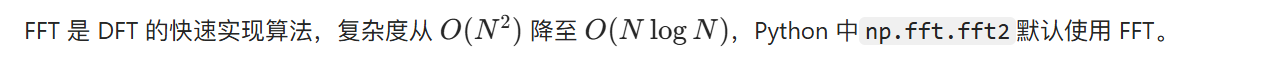
4.11.4 滤波器设计相关说明

  1. 滤波器需中心对齐（与 DFT 移位匹配）；
  2. 截止频率需根据图像尺寸归一化；
  3. 补零扩展可减少滤波后的边缘效应；
  4. 实值图像滤波后需取实部，避免虚部误差。

小结

核心知识点总结

  1. 频域滤波核心：将图像从空间域转换到频率域，通过修改频率分量实现增强 / 去噪，再逆变换回空间域；
  2. 滤波器分类 ：
    • 低通滤波（平滑）：理想低通（振铃）、巴特沃斯低通（适中）、高斯低通（无振铃）；
    • 高通滤波（锐化）：理想高通、巴特沃斯高通、高斯高通，高频强调滤波可提升亮度；
    • 选择性滤波：陷波滤波器可去除周期性噪声；
  3. 关键实现技巧 ：
    • 用np.fft.fft2/np.fft.ifft2实现 DFT/IDFT；
    • np.fft.fftshift将低频移到中心，便于滤波器设计；
    • 滤波后需取实部并归一化到 0-255。

实践建议

  1. 所有代码可直接运行，只需替换lena.jpg为自己的图像路径；
  2. 调整截止频率D0、阶数n等参数，观察滤波效果变化；
  3. 频域滤波的核心是理解 "低频对应整体、高频对应细节"，根据需求选择合适的滤波器。
相关推荐
HarmonLTS2 小时前
Pygame动画制作进阶（可直接运行，附核心原理）
python·pygame
他们叫我技术总监2 小时前
Python 列表、集合、字典核心区别
android·java·python
江沉晚呤时2 小时前
从零实现 C# 插件系统：轻松扩展应用功能
java·开发语言·microsoft·c#
木卫四科技2 小时前
Chonkie 技术深度学习
人工智能·python·rag
Knight_AL2 小时前
Java 多态详解：概念、实现机制与实践应用
java·开发语言
Omigeq2 小时前
1.2.1 - 图搜索算法（以A*为例） - Python运动规划库教程（Python Motion Planning）
开发语言·python·机器人·图搜索算法
资深流水灯工程师2 小时前
基于Python的Qt开发之Pyside6 串口接收数据被分割的解决方案
开发语言·python·qt
没有bug.的程序员2 小时前
Java 并发容器深度剖析：ConcurrentHashMap 源码解析与性能优化
java·开发语言·性能优化·并发·源码解析·并发容器
万行2 小时前
机器人系统ROS2
人工智能·python·机器学习·机器人·计算机组成原理
热门推荐
01GitHub 镜像站点022025 Telegram 最新免费社工库机器人（LetsTG可[特殊字符]）搭建指南（含 Python 脚本）03Linux下V2Ray安装配置指南042025年大语言模型技术全景报告05安娜的档案(Anna’s Archive) 镜像网站/国内最新可访问入口（持续更新）06UV安装并设置国内源07Labelme从安装到标注：零基础完整指南08BongoCat - 跨平台键盘猫动画工具09OpenCode 入门教程：介绍 · 安装 · 配置第三方 API (如 Claude)10jdk21下载、安装（Windows、Linux、macOS）