(leetcode)力扣100 45二叉树的右视图（dfs，bfs）

题目

给定一个二叉树的根节点 root，想象自己站在它的右侧，按照从顶部到底部的顺序，返回从右侧所能看到的节点值。

数据范围

二叉树的节点个数的范围是 [0,100]

-100 <= Node.val <= 100

测试用例

示例1

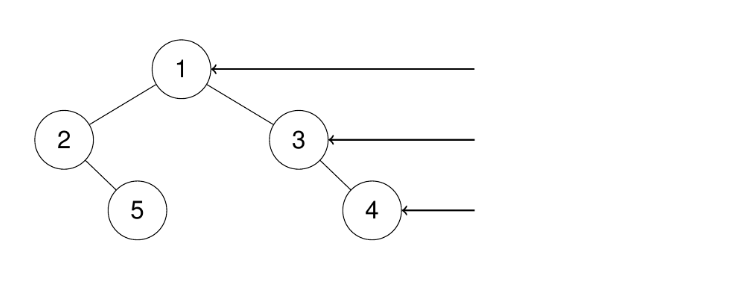
java 复制代码

输入：root = [1,2,3,null,5,null,4]

输出：[1,3,4]

示例2

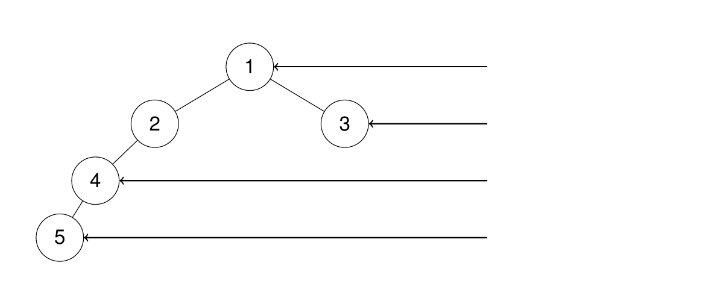
java 复制代码

输入：root = [1,2,3,4,null,null,null,5]

输出：[1,3,4,5]

示例3

java 复制代码

输入：root = [1,null,3]

输出：[1,3]

示例4

输入：root = []

输出：[]

题解1（dfs，迭代时空On）

java 复制代码

class Solution {
    public List<Integer> rightSideView(TreeNode root) {
        // key: 深度, value: 该深度最右边的节点值
        // 这个 Map 相当于"占位表"，每一层只允许一个节点占位
        Map<Integer, Integer> rightmostValueAtDepth = new HashMap<Integer, Integer>();
        int max_depth = -1;

        // 两个栈：一个存节点，一个存该节点对应的深度
        Deque<TreeNode> nodeStack = new LinkedList<TreeNode>();
        Deque<Integer> depthStack = new LinkedList<Integer>();
        
        nodeStack.push(root);
        depthStack.push(0);

        while (!nodeStack.isEmpty()) {
            TreeNode node = nodeStack.pop();
            int depth = depthStack.pop();

            if (node != null) {
            	// 维护最大深度，只是为了最后生成列表时知道循环几次
                max_depth = Math.max(max_depth, depth);

                // 【核心逻辑】
                // 只有当这个深度(depth) 第一次 出现时，我们才存入 Map。
                // 因为我们的遍历顺序是"根 -> 右 -> 左"，
                // 所以每一层"第一次"遇到的，一定是最右边的那个！
                if (!rightmostValueAtDepth.containsKey(depth)) {
                    rightmostValueAtDepth.put(depth, node.val);
                }

                // 【关键步骤】
                // 栈是"后进先出"。
                // 我们先 push 左子树，后 push 右子树。
                // 导致下一次 pop 的时候，会先拿出 右子树。
                nodeStack.push(node.left);
                nodeStack.push(node.right);
                
                // 记录对应的深度
                depthStack.push(depth + 1);
                depthStack.push(depth + 1);
            }
        }

        // 把 Map 里的结果转成 List
        List<Integer> rightView = new ArrayList<Integer>();
        for (int depth = 0; depth <= max_depth; depth++) {
            rightView.add(rightmostValueAtDepth.get(depth));
        }

        return rightView;
    }
}

题解2（dfs 递归时空on）

java 复制代码

class Solution {
    // 用于存放结果
    List<Integer> res = new ArrayList<>();

    public List<Integer> rightSideView(TreeNode root) {
        // 从根节点开始，当前深度为 0
        dfs(root, 0);
        return res;
    }

    // 递归函数
    private void dfs(TreeNode node, int depth) {
        // 1. 递归终止条件
        if (node == null) {
            return;
        }

        // 2. 核心逻辑："抢座"
        // 如果当前深度(depth) 等于 res的大小，说明这个深度是第一次到达！
        // 比如刚开始 depth=0, res.size()=0，记录进去。
        // 下一层 depth=1, res.size()=1，记录进去。
        // 如果后面又绕回 depth=1，但 res.size()已经是 2 了，就不记录了。
        if (depth == res.size()) {
            res.add(node.val);
        }

        // 3. 遍历顺序：非常关键！
        // 先去右边，确保右边的节点能最先抢到当前深度的位置
        dfs(node.right, depth + 1);
        
        // 再去左边
        // 如果右边已经把这一层的坑占了，左边这里的逻辑就不会触发 if(depth == res.size())
        dfs(node.left, depth + 1);
    }
}

题解3（bfs）

java 复制代码

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 * int val;
 * TreeNode left;
 * TreeNode right;
 * TreeNode() {}
 * TreeNode(int val) { this.val = val; }
 * TreeNode(int val, TreeNode left, TreeNode right) {
 * this.val = val;
 * this.left = left;
 * this.right = right;
 * }
 * }
 */
class Solution {
    public List<Integer> rightSideView(TreeNode root) {
        List<Integer> list = new ArrayList<>();
        // 特殊情况处理：空树直接返回空列表
        if (root == null) {
            return list;
        }

        // 使用队列进行广度优先搜索 (BFS)
        Queue<TreeNode> queue = new LinkedList<>();
        queue.add(root);

        // 外层循环：只要队列不空，说明还有下一层需要处理
        while (!queue.isEmpty()) {
            
            // 关键步骤：记录当前队列的大小 (num)
            // 这个 num 代表了当前这一层有多少个节点
            int num = queue.size();

            // 内层循环：只处理当前这一层的 num 个节点
            // 这里使用了后减运算符 (num--)：先判断 num!=0，然后 num 减 1
            while (num-- != 0) {
                // 弹出队首节点
                TreeNode temp = queue.poll();

                // 判断是否为该层的最后一个节点
                // 因为上面执行了 num--，当 num 变为 0 时，说明这是本层循环的最后一次迭代
                // 也就是遍历到了本层最右边的那个节点
                if (num == 0) {
                    list.add(temp.val);
                }

                // 标准 BFS 操作：将子节点加入队列，等待下一层处理
                // 注意顺序：先放左，再放右
                if (temp.left != null) {
                    queue.add(temp.left);
                }
                if (temp.right != null) {
                    queue.add(temp.right);
                }
            }
        }

        return list;
    }
}

思路

这道题挺简单的一道题，就是在正常搜索树的时候最一些条件判断，即可满足要求，无论是bfs和dfs都能够很好完成这一点。