【数据结构学习】

数据结构/软件工程，能回顾的都回顾一下

图

1. 不可能为空图，至少包含一个顶点。树可以为空树

2. 有向完全图边为n(n-1)；无向完全图边为n(n-1) / 2；

3. 连通图：任意两顶点之间都有路径可以连通；完全图：任意两点之间都有直接连接的路径

4. 权值：边代表的权值

最小生成子树------目的是用权值最小（代价最小）的边连通

1. 解决什么问题：通过连接图上权值最小的边，使得图成为连通图。

2. 应用：在网络连接上，花费最少的材料使得局域网连通

3. 最小生成子树------Prim算法

（1）适用于 顶点较少的图，是一个不断把顶点加入的过程

（2）步骤：

①初始化一棵空树

②选择图中任一顶点加入树中

③从图中选择一条权值最小 且不会构成回路的边，加入到树中

④并把相应的顶点也加入树中

⑤重复步骤③④直到图上所有的顶点都 加入到树中

（3）使用prim算法：当图中权值各不相同时，最小生成树唯一；当存在相同权值的边时，生成树可能不唯一。

（4）例题：

忘记把4画上去了，将就看吧

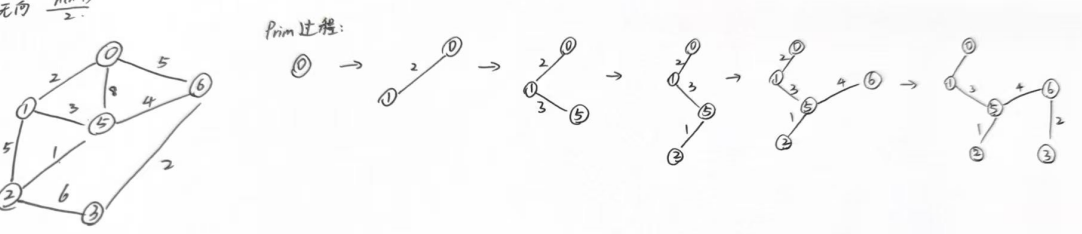
（5）伪代码

void Prim(G, T) // G为图，T为树
Begin
    T = 空树
    T = {w} //w为图上任意一个顶点
    while (V - U != 空集) //V为图上顶点的集合，U为树上节点的集合
    {
        选择u∈U，v∈V-U，且(u,v)是权值最小的边
        U = U + {v}  //将顶点v加入树中
        T = T U (u,v) //将这条权值最小的边加入树中
    }
End

4. 最小生成子树------Kruskal算法

（1）适用：边数较少的图，不断加入边的过程

（2）步骤：

①将图上所有顶点加入森林中

②从侯选边中选择一条权值最小的边，在森林中不能形成回路，加入到森林中

③重复步骤②，直到森林中所有的节点都连通

（3）例题说明

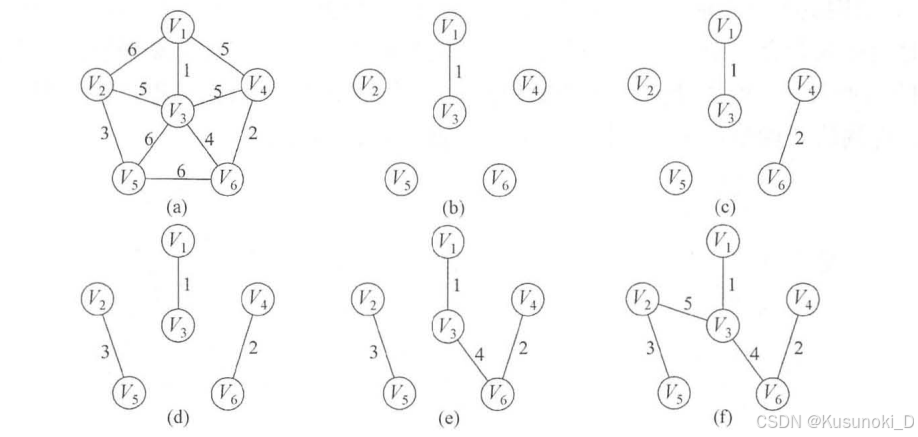
（4）伪代码

void Kruskal(V,T) //V为图上所有顶点的集合，T为树
Begin
    T = V; //将图上所有顶点加入树中
    nums = n; //n为图中顶点个数，每个顶点自成一个连通分量
    while (nums > 1)
    {
        选择(u,v)是权值最小的边，且u，v属于不同的连通分量
        T = T U (u,v) //将这条边加入树中
        nums--;
    }
End

5. Prim和Kruskal说明

（1）Prim和Kruskal得到的最小生成树可能不同

（2）Prim每次得到的最小生成树都不一定相同 （可能存在权值相同的边）

（3）Prim和Kruskal得到最小生成树的代价是相同的 ！

（4）在Prim和Kruskal中，在所选边的基础上，额外选边时，一定不能形成回路

图的遍历

参考：https://zhuanlan.zhihu.com/p/685010225

1. DFS深度优先遍历方法

（1）步骤

类似树的先序遍历：每次不撞南墙不回头，使用递归的思想遍历 for循环

【标准语句】

• 从图中某个顶点v出发，访问v。
• 找出刚访问过的顶点的第一个未被访问的邻接点，访问该顶点。以该顶点为新的刚访问过的顶点，重复该步骤，直至刚访问过的顶点没有未被访问的邻接点为止。
• 返回前一个访问过的且仍有未被访问的邻接点的顶点，找出该顶点的下一个未被访问的邻接点，访问该顶点。
• 重复第二步和第三步，直至图中所有顶点都被访问过，搜索结束。

【我的说法】

①初始化数组visitied[n]=0,n为图中顶点个数，用于记录顶点访问情况，不重复访问

②从图的某个顶点v出发，访问该顶点。

③找出刚访问过顶点的第一个未被访问过的邻接点，访问该顶点。

④以该顶点作为新的刚访问过的顶点，重复该步骤，直到刚访问过的顶点的所有相邻点均被访问为止。

⑤返回上一个访问过的 且有未被访问的邻接点的顶点，找出该顶点的下一个未被访问的邻接点并访问。

⑥重复③④步骤，直到图上所有顶点均被访问过，搜索结束。

（2）DFS遍历例题

无向图：V1-V2-V4-V8-V5-V3-V6-V7

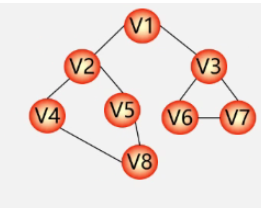
有向图（树的先序遍历）：V1-V2-V5-V4-V3 或 V1-V3-V4-V5-V2

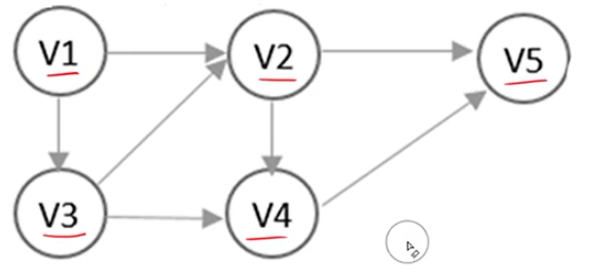
（3）DFS遍历伪代码
for循环的递归算法 时间复杂度O(n^2)

递归思想，需要借助递归工作栈，

visitied[n] = 0; // n为图中顶点个数
void DFS(G,v)        // G为要访问的图，v为图的初始顶点
Begin
    visited[v] = 1;
    for (v的所有相邻节点w; w存在;)
    {
        if (visited[w] == 0)
        {
            DFS(G,w);
        }
    }
End

2. 广度优先遍历

（1）思想：使用队列思想

（2）步骤：

①为了避免同一顶点被访问多次，初始化visited[n]数组，n为顶点个数，初始状态值全为0

②访问图的某个顶点v，visitied[v]=1，接着将该顶点入队列Q，

③当队列Q不为空时，重复以下步骤：

先将队头元素w出队，

再依次访问w的每个相邻节点w1，若w1未被访问过，则访问该节点，visitied[w1]=1，并将其加入队列

（3）BFS伪代码：时间复杂度O(n^2)。每个元素只入队一次

visited[n] = 0; //n为图中顶点个数
void BFS(G,v)
Begin
    InitQueue(Q); // 初始化队列Q
    visitied[v]=0;    //访问顶点v
    Enqueue(Q,v); //将顶点v加入队列
    while (!Q) //Q非空时，循环
    {
        Dequeue(Q,u); //从队列中取出第一个顶点，命名为u
        for(u的每一个相邻节点w;w存在;)
        {
            if (visited[w] == 0) 
            {
                visited[w] = 1;
                Enqueue(Q,w);
            }
        }
    }

End

图的拓扑排序AOV------目的是找到顺序

1. 目的：在有向无环图中，找出图上各顶点的顺序，不唯一。

2. 应用：常用来对有依赖关系的任务进行排序，有向无环图常用来表示活动之间的依赖关系，也叫AOV网。

在工程中，可以使用拓扑排序列出子过程的先后顺序，按照顺序即可完成整个工程

在软件模块编译中，通过拓扑排序找到模块之间的依赖关系，按照依赖顺序编译，即可编译整个工程。

在课程学习中，某门课程存在先修课，这时可以对课程进行建模，利用拓扑结构找到课程学习顺序。

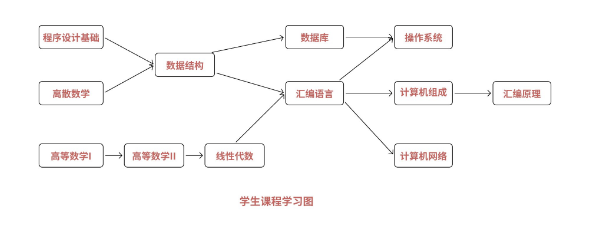
3. 拓扑排序过程：

（1）从图中找到入度为0的顶点，作为访问的第一个节点

（2）从图中删去该顶点和相关的弧或边

（3）从剩余顶点中再找出入度为0的顶点，重复（1）（2），直到图上所有的顶点均被列出，得出的结果即为该图的拓扑排序

4. 例题 1-2-4-3-5
   

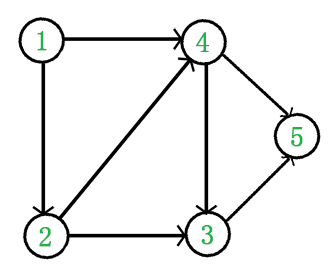
5. Kahn算法------基于队列的调度算法

参考：https://cloud.tencent.com/developer/article/2617334

初始化：①初始化队列，将图中所有入度为0的点加入队列

迭代：②从队列中取出队头元素v，加入到拓扑排序中，将该顶点及其所有相邻的边<u,v>从图中删去

③若此时顶点v也变为入度为0的点，则将顶点V加入队列

④重复2-3，直到队列为空

⑤若此时拓扑排序的顶点个数与图中顶点个数相等，则排序成功，否则排序失败

相应伪代码如下：

void karn(G,v)
Begin
    int degrees[n];    //存放图中各顶点的入度
    InitQueue(Q); //初始化队列
    vector<int> topo; //存储拓扑排序序列（因为不知道n为多少，使用vector更合理）
    for (int i=0;i<n;i++)
    {
        if (degrees[n]==0)
        {
            Enqueue(Q,i); //将入度为0的点入队
        }
    }

    while(!Q)
    {
        Dequeue(Q,v); //从队头中取出元素
        topo.push(v);
        for (v的每个相邻顶点u)
        {
            degrees[u]--;
            if (degress[u]==0)
            {
                Enqueue(Q,u);
            }
        }
    }
    if (topo.size() == n) 
    {
        printf("拓扑排序成功");
    } else {
        printf("拓扑排序失败");
    }
End

图的最短路径------目的是找到两点之间最短距离

1. 通过找到A点和B/C/D之间最短距离，近而求得A与终点之间的最短距离

2. 步骤

①以图中初始顶点v作为入口，计算v到相邻顶点的距离，若v无法到达某个顶点，则记为∞。存储在数组中，一轮结束后，比较出距离最短的路径<v,w>，即可得出v到w的最短距离

②以v,w作为路径的一部分，找出v,w到其他顶点的距离，存储在数组中，一轮结束后，比较出最短的距离<w,i>，此时即可得出v到i的最短距离

③重复步骤②，直到找出v到终点的最短距离

3. 算法伪代码------迪杰斯特拉算法

适用于：求某个顶点到其他所有顶点之间的最短路径（单源），不允许权值为负数

todo迪杰斯特拉好难 学不会

4. 算法伪代码------Floyd算法

迪杰斯特拉算法，只能一次计算出某个点到其他点之间的最短距离，比如A到BCD点之间最短距离

Floyd算法可以一次性计算出所有点之间的最短距离。适用于稠密图。

基于动态规划的思想：map[i][j] = min(map[i][j], map[i][k] + map[j][k])。比较：i到j之间的距离 VS i通过k中转到j的距离

void Floyd() 
{
Begin
    for(int i = 0; i < num; i++)
    {
        for(int j = 0; j < num; j++)
        {
            for(int k = 0; k < num; k++)
            {
                if (map[i][j] > map[i][k] + map[k][j])
                {
                    map[i][j] = map[i][k] + map[k][j];
                }
            }
        }
    }
End
}

图的最快完成时间AOE网------关键路径 关键活动 活动余量 最长时间

1.应用：在工程管理上，通过计算关键路径和关键活动，可以判断出完成一项工程所需要的最少时间，和所必须要完成的活动。

在工程管理上，可以优先压缩关键活动的工期，其余活动可以灵活安排

2.关键路径：我从哪里来，我要当最大。

只有先完成需要时间最长的步骤后，才能开展下一步活动。

3. 活动余量

关键活动余量0，不能晚开始

非关键活动余量=关键路径+包围法