题目
给定两个整数数组 preorder 和 inorder ,其中 preorder 是二叉树的先序遍历, inorder 是同一棵树的中序遍历,请构造二叉树并返回其根节点。
数据范围
1 <= preorder.length <= 3000
inorder.length == preorder.length
-3000 <= preorder[i], inorder[i] <= 3000
preorder 和 inorder 均 无重复 元素
inorder 均出现在 preorder
preorder 保证 为二叉树的前序遍历序列
inorder 保证 为二叉树的中序遍历序列
测试用例
示例1
java
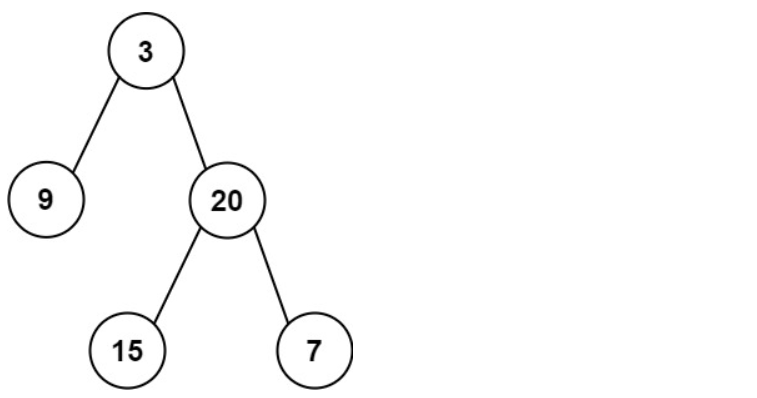
输入: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
输出: [3,9,20,null,null,15,7]示例2
java
输入: preorder = [-1], inorder = [-1]
输出: [-1]题解1(递归,时空On)
java
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
// 使用 HashMap 存储中序遍历的值和索引,以便 O(1) 复杂度快速定位根节点
// 注意:在 LeetCode 中写 static 可能会导致多组测试用例间数据污染,最好去掉 static 或在函数内初始化
static HashMap<Integer,Integer> map;
public TreeNode buildTree(int[] preorder, int[] inorder) {
map = new HashMap<>();
int len = inorder.length;
// 预处理:将中序遍历的值与索引存入 Map
for(int i = 0; i < len; i++){
map.put(inorder[i], i);
}
// 开启递归,初始范围是整个数组
return myBuildTree(preorder, inorder, 0, preorder.length - 1, 0, inorder.length - 1);
}
/**
* @param preorder_left 当前子树在前序数组的左边界
* @param preorder_right 当前子树在前序数组的右边界
* @param inorder_left 当前子树在中序数组的左边界
* @param inorder_right 当前子树在中序数组的右边界
*/
public TreeNode myBuildTree(int[] preorder, int[] inorder, int preorder_left, int preorder_right, int inorder_left, int inorder_right){
// 终止条件:如果不构成区间(左边界大于右边界),说明节点为空
if(preorder_left > preorder_right){
return null;
}
// 1. 前序遍历的第一个元素就是当前子树的根节点
TreeNode root = new TreeNode(preorder[preorder_left]);
// 2. 在中序遍历中找到根节点的位置
int order_root = map.get(root.val);
// 3. 关键步骤:计算左子树的节点数量
// 公式:根在中序的位置 - 中序起始位置
int t_num_left = order_root - inorder_left;
// (注:这个变量 t_num_right 其实在后面没用到,因为右边界可以直接推导)
int t_num_right = inorder_right - order_root;
// 4. 递归构造左子树
// pre范围:[根节点索引+1, 根节点索引+左子树长度]
// in 范围:[左边界, 根节点在中序位置-1]
root.left = myBuildTree(preorder, inorder,
preorder_left + 1,
preorder_left + t_num_left,
inorder_left,
order_root - 1);
// 5. 递归构造右子树
// pre范围:[根节点索引+左子树长度+1, 右边界]
// in 范围:[根节点在中序位置+1, 右边界]
root.right = myBuildTree(preorder, inorder,
preorder_left + t_num_left + 1,
preorder_right,
order_root + 1,
inorder_right);
return root;
}
}题解2(迭代,时空On)
java
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public TreeNode buildTree(int[] preorder, int[] inorder) {
// 1. 健壮性检查:既要防空指针,也要防空内容
if(preorder == null || preorder.length == 0){
return null;
}
// 2. 初始化:前序遍历的第一个必定是整棵树的根
TreeNode root = new TreeNode(preorder[0]);
int index = 0; // 指向中序遍历数组的指针
int len = preorder.length;
// 3. 使用栈来模拟递归过程,栈中存放的是"还未处理右子树"的节点
Deque<TreeNode> deque = new ArrayDeque<>();
deque.push(root);
// 4. 遍历前序数组剩下的元素
for(int i = 1; i < len; i++){
// 获取当前栈顶节点(潜在的父亲)
TreeNode node = deque.peek();
// 获取前序遍历中的当前值(我们要插入的新节点)
int curr = preorder[i];
// 5. 情况A:栈顶节点的值 != 中序遍历当前值
// 含义:说明还没有到达左边界的最底部,我们还在"往左冲"的路上。
// 动作:当前 curr 必定是 node 的左孩子。
if(node.val != inorder[index]){
node.left = new TreeNode(curr);
deque.push(node.left); // 将新节点入栈,因为它也可能还有左孩子
}
// 6. 情况B:栈顶节点的值 == 中序遍历当前值
// 含义:说明在这个节点处,左子树已经走完了(或者没有左子树),该考虑往右走了。
else {
// 回溯逻辑:不断出栈,直到找到那个"缺右孩子"的祖先节点。
// 只要栈顶元素等于中序数组当前指向的元素,就说明这个节点及其左子树处理完毕了。
while(!deque.isEmpty() && deque.peek().val == inorder[index]){
node = deque.pop(); // 关键点:node不断更新,最后停留在即将连接右孩子的父节点上
index++; // 中序指针后移
}
// 此时的 node 就是 curr 的父节点
node.right = new TreeNode(curr);
deque.push(node.right); // 将新节点入栈
}
}
return root;
}
}思路
这道题虽然是中等题,但是使用递归方法实现还是算比较容易的,只需要我们理清,每一次递归的左右子树,他们在先序序列与中序序列的范围即可,理清后,就是一个简单的二叉树递归问题了。
这道题的迭代方法比较麻烦,他是通过遍历前序序列,因为前序序列存在性质"当我们遍历 preorder 数组时,相邻的两个数,后者要么是前者的左孩子,要么是前者(或前者某个祖先)的右孩子"。那么如何进行判决到底是左孩子还是某个祖先的右孩子呢,这个时候就需要用到中序序列,我们提前创建变脸index来遍历中序序列,如果栈顶的元素与中序序列相同则是后者,反之。
理清这个逻辑之后,我们就可以开始模拟了。