【剑斩OFFER】算法的暴力美学——力扣 1926 题：迷宫中离入口最近的出口

橘颂TA2026-01-21 9:02

一、题目描述

二、算法原理

思路：BFS 算法

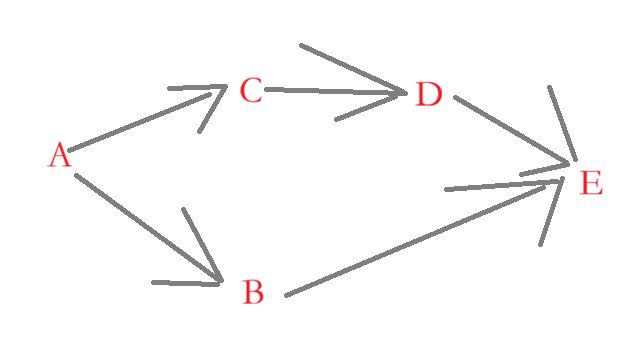
我们看到上面这张图片，求 A 到 E 的最短路径，此时我们可以使用一个队列来实现层序遍历来实现 BFS 算法，我们先把 A 入队列，假设两点之间的距离都为 1，所以此时队列情况：

A -> B -> C

此时因为 B 下一个就是 E 了，所以：

A -> B -> C-> E，那么 D 就没有必要入队列了，因为 E 已经找到了，那么最短路径的长度就是

剥离的次数：

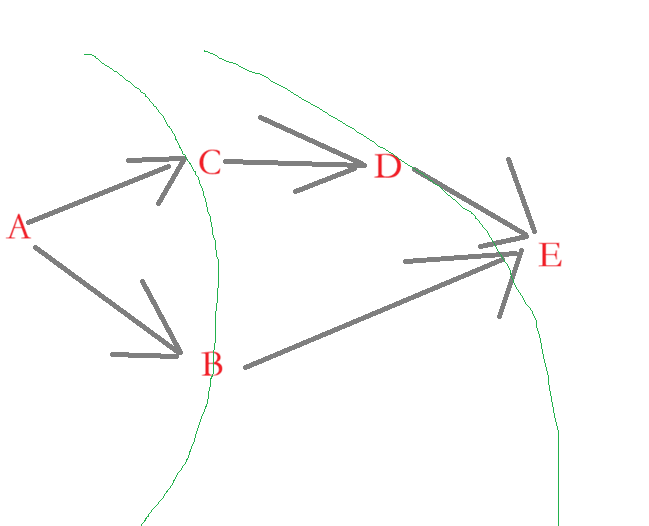
这道题目和这个示例的解法一样，只不过我们要创建一个和原二维数组的一样大小的数组用来标记哪些值被遍历的，不要重复遍历；

三、代码实现

cpp 复制代码

class Solution {
    int dx[4] = {1,-1,0,0};
    int dy[4] = {0,0,1,-1};
    bool tmp[200][200];
    typedef pair<int,int> PII;
public:
    int nearestExit(vector<vector<char>>& maze, vector<int>& enter) {
        int x = enter[0], y = enter[1];

        queue<PII> que;//使用层序遍历
        que.push({x,y});
        tmp[x][y] = true;

        int count = 0;
        while(que.size())
        {
            int forl = que.size();
            
            count++;//最短的剥离次数就是最短路径
            while(forl--)//控制剥离的层数
            {
                auto [a,b] = que.front();
                que.pop();
                for(int i = 0; i < 4; i++)
                {
                    x = a + dx[i];
                    y = b + dy[i];

                    if(x >= 0 && x < maze.size() && y >= 0 && y < maze[0].size() && maze[x][y] == '.' && tmp[x][y] == false)
                    {
                        if(x == maze.size() - 1 || x == 0)//到达出口
                        {
                            return count;
                        }
                        else if(y == maze[0].size() - 1 || y == 0)//到达出口
                        {
                            return count;
                        }
                        else
                        {
                            tmp[x][y] = true;
                            que.push({x,y});
                        }
                    }
                 }
            }
        }
        return -1;
    }
};