项目：矿物分类（训练模型）

根据上一篇博客我们对数据清洗得到了分别使用平均值，众数，中位数，只获取完整行，线性回归，逻辑森林这六种填充方法，获得了完整数据，可以用来训练模型。

就是我们比较熟悉的环节，会分别用，逻辑回归，随机森林，svm，adaboost，高斯贝叶斯，xgboost，全连接神经网络，卷积神经网络进行训练

一、读取数据，这里result_all={}是用来存储最终结果的，每一种填充方法对应八种模型训练的结果

import pandas as pd
from sklearn import metrics

train_data=pd.read_excel(r"D:\learn\temp_data\训练集[方法].xlsx")
x_train_data=train_data.iloc[:,1:]
y_train_data=train_data.iloc[:,0]

test_data=pd.read_excel(r"D:\learn\temp_data\测试集[方法].xlsx")
x_test_data=test_data.iloc[:,1:]
y_test_data=test_data.iloc[:,0]

result_all={}

二、训练方法

在使用算法之前需要介绍一种方法，网格搜索

对于之前的学习中我们通常使用交叉验证进行调参，对一个参数寻找最优值我们就需要使用一次交叉验证，当我们有很多个参数需要调节的时候，交叉验证就显得很笨重，所以我们使用网格搜索。网格搜索本质上也是交叉验证，但是网格搜索能一下筛选多个参数的最优值。

我们拿逻辑回归的参数进行举例：

导入这个模块，然后把每个参数列出来，和可以选择的值，这是一般写法，但是以下参数为逻辑回归的参数，这样写会出错。

from sklearn.model_selection import GridSearchCV
param_grid={
    'solver':['newton-cg','lbfgs','liblinear','sag','sags'],
    'penalty':['l1','l2','elasticnet','none'],#正则化类型
    'C':[0.01,0.1,1,10],
    'max_iter':[100,200,500],
    'multi_class':['auto','ovr','multinomial'],
}

由于none惩罚的时候，不支持multinomial等，其他参数之间的限制，所以我们要分开写，这里方法改为设置一个列表用来保存得到最优值的结果，最后在对这四组获得的值进行筛选，选出最优的参数值

#网格搜索方法进行调参
grid_chioce=[]
grid_chioce.append({
    'penalty': ['l1', 'l2'],  # 正则化类型
    'C': [0.01, 0.1, 1, 10],
    'solver': ['liblinear'],#linlinear一般收敛比较快迭代次数可以少些
    'max_iter': [100, 200],
    'multi_class': [ 'ovr'],
    })
grid_chioce.append({
    'solver': ['newton-cg', 'lbfgs'],
    'penalty': ['l2'],  # 正则化类型
    'C': [ 0.01, 0.1, 1, 10],
    'max_iter': [100, 200, 500],
    'multi_class': [ 'ovr', 'multinomial'],
    })
grid_chioce.append({
        'solver': ['saga'],
        'penalty': ['l1','l2'],  # 正则化类型
        'C': [0.01, 0.1, 1, 10],
        'max_iter': [100, 200, 500],
        'multi_class': ['ovr', 'multinomial'],
    })
grid_chioce.append({
        'solver': ['soga'],
        'penalty': ['elasticnet'],  # 正则化类型
        'C': [0.01, 0.1, 1, 10],
        'max_iter': [100, 200, 500],
        'multi_class': ['ovr', 'multinomial'],
        'l1_ratio': [0.1, 0.5, 0.9]  # 仅当penalty='elasticnet'时使用
    }
)
logic=LogisticRegression()
grid_search=GridSearchCV(logic,grid_chioce,cv=5)
grid_search.fit(x_train_data,y_train_data)
print('最佳参数：{}'.format(grid_search.best_params_))

网格搜索过程比较慢，这里我们直接使用已知比较好的参数值来进行训练模型

1.逻辑回归

from sklearn.linear_model import  LogisticRegression

'''建立最优模型'''
Logic_result={}
Logic=LogisticRegression(C=0.001,max_iter=100,penalty='none',solver='lbfgs')
Logic.fit(x_train_data,y_train_data)

'''测试结果'''
train_pre=Logic.predict(x_train_data)
print('逻辑回归train:\n',metrics.classification_report(y_train_data,train_pre))
test_pre=Logic.predict(x_test_data)
print('逻辑回归test:\n',metrics.classification_report(y_test_data,test_pre))
a=metrics.classification_report(y_test_data,test_pre,digits=6)
b=a.split()

Logic_result['recall_0']=float(b[6])
Logic_result['recall_1']=float(b[11])
Logic_result['recall_2']=float(b[16])
Logic_result['recall_3']=float(b[21])
Logic_result['acc']=float(b[25])
result_all['Logic']=Logic_result
print('结束！')

2.随机森林

from sklearn.ensemble import RandomForestClassifier
forest_result={}
forest=RandomForestClassifier(bootstrap=False,
                          max_depth=20,
                          max_features='log2',
                          min_samples_leaf=1,
                          min_samples_split=2,
                          n_estimators=50,
                          random_state=487)
forest.fit(x_train_data,y_train_data)

train_pre=forest.predict(x_train_data)
print('逻辑回归train:\n',metrics.classification_report(y_train_data,train_pre))
test_pre=forest.predict(x_test_data)
print('逻辑回归test:\n',metrics.classification_report(y_test_data,test_pre))
forest_test_report=metrics.classification_report(y_test_data,test_pre,digits=6)
b=forest_test_report.split()

forest_result['recall_0']=float(b[6])
forest_result['recall_1']=float(b[11])
forest_result['recall_2']=float(b[16])
forest_result['recall_3']=float(b[21])
forest_result['acc']=float(b[25])
result_all['forest']=forest_result
print('结束！')

3.svm

代码都是差不多的，基本上是下面这三点，其他修改一下

from sklearn.svm import SVC
SVM_result={}
SVM=SVC(C=1,coef0=0.1,degree=4,gamma=1,kernel='poly',probability=True,random_state=100)

4.Adaboost（和上面一样）

from sklearn.ensemble import AdaBoostClassifier
from sklearn.tree import DecisionTreeClassifier
Adaboost_result={}
Adaboost=AdaBoostClassifier(algorithm='SAMME',
                       base_estimator=DecisionTreeClassifier(max_depth=2),
                       n_estimators=200,
                       learning_rate=1.0,
                       random_state=0)

5.高斯贝叶斯（贝叶斯几乎没什么调节的参数，其他和上面一样，修改一下就可以）

from sklearn.naive_bayes import GaussianNB
GNB_result={}
GNB=GaussianNB()

6.Xgboost（一样，不过这里有一点需要注意，就是xgboost可能不在sklearn，需要我们自己下载，就相当于下载一个库）

import xgboost as xgb  #Xgboost库需要下载
xgb_result={}
xgb=xgb.XGBClassifier(learning_rate=0.05,
                      n_estimators=200,
                      num_class=5,
                      max_depth=7,
                      min_child_weight=1,
                      gamma=0,
                      subsample=0.6,
                      colsample_bytree=0.8,
                      objective='multi:softmax',
                      seed=0)

7.全连接神经网络

到神经网络，就跟上面机器学习的算法不一样了

神经网络不能接收表格，数据必须转化为张量数据，其实张量就是矩阵

Float32，表示精度有多高，32就是32位空间，16就是16个空间，从而控制精度

import torch
import torch.nn as nn
import torch.optim as optim
import numpy as np
from sklearn.model_selection import train_test_split

#转换数据为pytorch张量
x_train=torch.tensor(x_train_data.values,dtype=torch.float32)
y_train=torch.tensor(y_train_data.values)
x_test=torch.tensor(x_test_data.values,dtype=torch.float32)
y_test=torch.tensor(y_test_data.values)

linear全连接，init只是定义了神经网络，forward表示神经网络层搭建好

这里我们设置了三层神经网络，虽然只有三层但不代表只能进行三次变换，实际上可以通过激活函数引入多层复合，实现复杂的特征映射。每一层的输出都可以作为下一层的输入，不断抽象和组合特征，从而拟合高度非线性的决策边界。只要网络足够深或宽，配合合适的训练策略，就能逼近任意连续函数。

#定义神经网络
class Net(nn.Module):
    def __init__(self):
        super(Net,self).__init__()
        self.fc1=nn.Linear(13,32)
        self.fc2=nn.Linear(32,64)
        self.fc3=nn.Linear(64,4)

    def forward(self,x):
        x=torch.relu(self.fc1(x))
        x=torch.relu(self.fc2(x))
        x=self.fc3(x)
        return x

loss损失函数，损失函数有五种，0-1损失函数用于二分类，回归用均方差损失函数，多分类用交叉熵损失函数。这里就是交叉熵损失函数。

（所有的权重一开始是有个初始值的，随机给值，但不是绝对的随机，是有控制的给值【正态分布】根据损失来改变w的过程就是梯度下降）

#实例化网络，损失函数和优化器
model=Net()
criterion=nn.CrossEntropyLoss()
optimizer=torch.optim.Adam(model.parameters(),lr=0.001)

def evaluate_model(model,x_data,y_data,train_or_test):
    size=len(x_data)
    with torch.no_grad():
        predicictions=model(x_data)
        correct=(predicictions.argmax(1)==y_data).type(torch.float).sum().item()
        correct /= size
        loss=criterion(predicictions,y_data).item()
        print(f'{train_or_test}:\t Accuracy:{(100 * correct)}%')
    return  correct

Zero_gard梯度的初始化

outputs=model......model后面有个forward是省略的，覆盖父类的方法，所以这里能直接把x_train传进

epochs1=10000
accs=[]
for epoch in range(epochs1):
    optimizer.zero_grad()
    outputs=model(x_train)

    loss=criterion(outputs,y_train)
    loss.backward()
    optimizer.step()
    if(epoch+1)% 100 ==0:
        print(f'Epoch [{epoch +1}/{epochs1},Loss:{loss.item():.4f}')
        train_acc=evaluate_model(model,x_train,y_train,'train')
        test_acc=evaluate_model(model,x_test,y_test,'test')
        accs.append(test_acc * 100)

net_result={}
net_result['acc']=max(accs)
result_all['linear-net']=net_result

8.卷积神经网络

和全连接不同的地方就在于神经网络构建

conv2d和1d的区别，2d是用来识别图片，卷积核是二维的，最小单元是一张图

1d的最小单元是一行数据，卷积核是一维的，同样3d就是用来处理视屏的，卷积核是三维的。

out_channels和size代表的就是16个卷积核，卷积核是3

import torch
import torch.nn as nn
import torch.optim as optim
import numpy as np

#转换数据为pytorch张量
x_train=torch.tensor(x_train_data.values,dtype=torch.float32)
y_train=torch.tensor(y_train_data.values)
x_test=torch.tensor(x_test_data.values,dtype=torch.float32)
y_test=torch.tensor(y_test_data.values)

class CNN(nn.Module):
    def __init__(self,num_features,hidden_size,num_classes):
        super(CNN,self).__init__()
        self.conv1=nn.Conv1d(in_channels=1,out_channels=16,kernel_size=3,padding=1)
        self.conv2=nn.Conv1d(in_channels=16,out_channels=32,kernel_size=3,padding=1)
        self.conv3=nn.Conv1d(in_channels=32,out_channels=64,kernel_size=3,padding=1)
        self.relu=nn.ReLU()
        self.fc=nn.Linear(64,num_classes)

    def forward(self,x):
        x=x.unsqueeze(1)
        x=self.conv1(x)
        x=self.relu(x)
        x=self.conv2(x)
        x=self.relu(x)
        x=self.conv3(x)
        x=self.relu(x)
        x=x.mean(dim=2)
        x=self.fc(x)
        return x

hidden_size=10
num_classes=4
model=CNN(13,hidden_size,num_classes)
criterion=nn.CrossEntropyLoss()
optimizer=optim.Adam(model.parameters(),lr=0.001)

epochs2=10000
accs=[]
for epoch in range(epochs2):
    outputs=model(x_train)
    loss=criterion(outputs,y_train)
    optimizer.zero_grad()
    loss.backward()
    optimizer.step()

    if(epoch+1)% 100 ==0:
        print(f'Epoch [{epoch +1}/{epochs2},Loss:{loss.item():.4f}')

        with torch.no_grad():
            predictions=model(x_train)
            predicted_classes=predictions.argmax(dim=1)
            accuracy=(predicted_classes == y_train).float().mean()
            print(f'train accuracy:{accuracy.item() * 100:.2f}%')

            predictions=model(x_test)
            predicted_classes=predictions.argmax(dim=1)
            accuracy=(predicted_classes == y_test).float().mean()
            print(f'test accuracy:{accuracy.item() * 100:.2f}%')
            accs.append(accuracy*100)

cnn_result={}
cnn_result['acc']=max(accs).item()
result_all['cnn']=cnn_result

三、保存结果

上面就是我们八种训练方法，最后我们需要对六个填充方法，八个训练方法的48个结果进行保存

print(result_all)
import json
result={}
result['方法 fill']=result_all
with open(r'temp_data/result[方法].json','w',encoding='utf-8')as file:
    json.dump(result,file,ensure_ascii=False,indent=4)

接着开头对文件的读取，读取什么填充方法的数据，最后这里就写上对应的方法，我们能得到六个文件

一个文件是一种填充方法的八个训练方法的结果

eg：

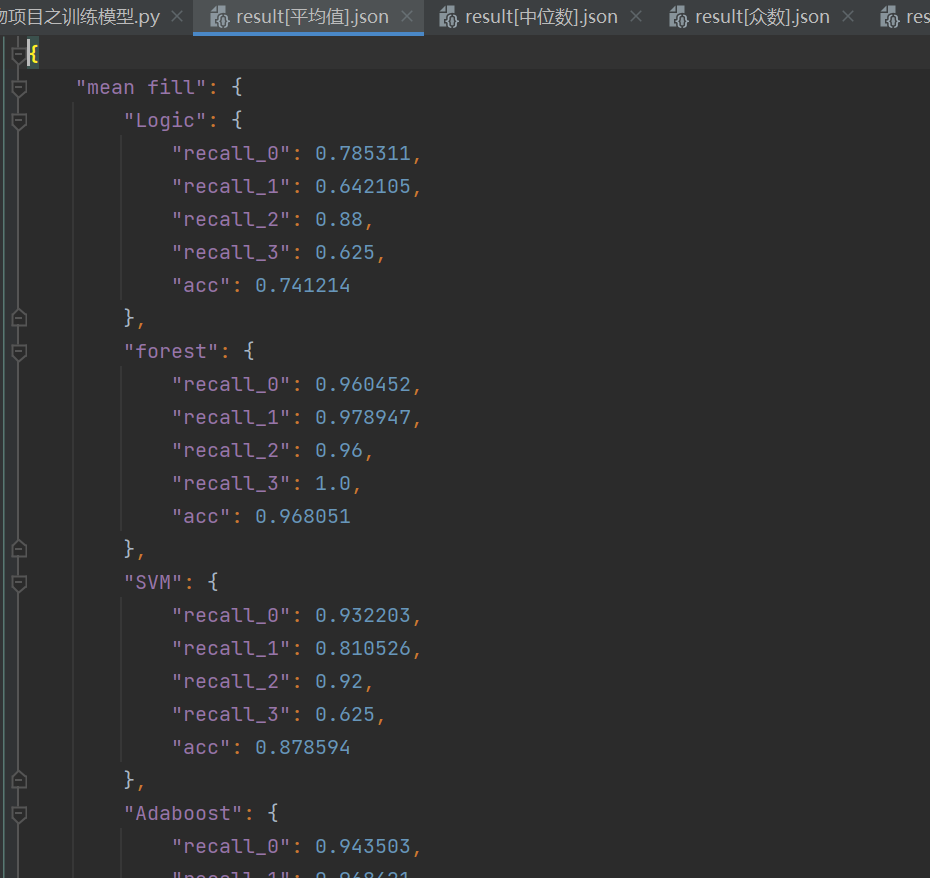
最后对比，中位数填充，随机森林训练的准确率最高