视频讲解:GESP2025年3月四级C++真题讲解
一、单选题
第1题

解析:
答案A,
第2题

解析:
答案B,func()函数输出20 ,main函数内输出10
第3题

解析:
答案B,*p表示a变量
第4题

解析:
答案D,函数有值传递、引用传递、指针传递,只有值传递会拷贝
cpp
#include <bits/stdc++.h>
using namespace std;
// 1. 传值传递:无法交换实参
void swap1(int a, int b) {
int temp = a;
a = b;
b = temp;
}
// 2. 指针传递:通过地址交换实参
void swap2(int* a, int* b) {
int temp = *a;
*a = *b;
*b = temp;
}
// 3. 引用传递:通过别名交换实参(C++特有)
void swap3(int& a, int& b) {
int temp = a;
a = b;
b = temp;
}
int main() {
int x = 10, y = 20;
// 传值传递测试
swap1(x, y);
cout << "传值后:" << x << " " << y << endl; // 10 20(未交换)
// 指针传递测试
swap2(&x, &y);
cout << "指针传递后:" << x << " " << y << endl; // 20 10(已交换)
// 引用传递测试
swap3(x, y);
cout << "引用传递后:" << x << " " << y << endl; // 10 20(再次交换)
return 0;
}第5题

解析:
答案D,实参y使用了引用传递,会改变,所以y变1
第6题

解析:
答案C,AD语法有误;B选项:main函数不可以赋值,只能定义声明
第7题

解析:
答案D,嵌套太多,会造成逻辑复杂,可维护和可读性差
第8题

解析:
答案D,
cpp
a[0][0] = 1 ,a[0][1] = 2 ,a[0][2] = 3
a[1][0] = 4 ,a[1][1] = 5 ,a[1][2] = 6第9题

解析:
答案B,只有b符合语法
第10题

解析:
答案B,
cpp
先计算f1+f2(res=f1+f2)
再f1后移 (f1=f2)
最后f2后移 (f2=res)第11题

解析:
答案B,

第12题

解析:
答案B,B选项就是稳定排序的定义
第13题

解析:
答案A,
cpp
初始状态:5 3 8 1
第1次比较:(5 3) 8 1
第2次比较:3 (5 8) 1
第3次比较:3 5 (8 1)
第1轮冒泡后的状态:3 5 1 8第14题

解析:
答案A,根据以下顺序运行
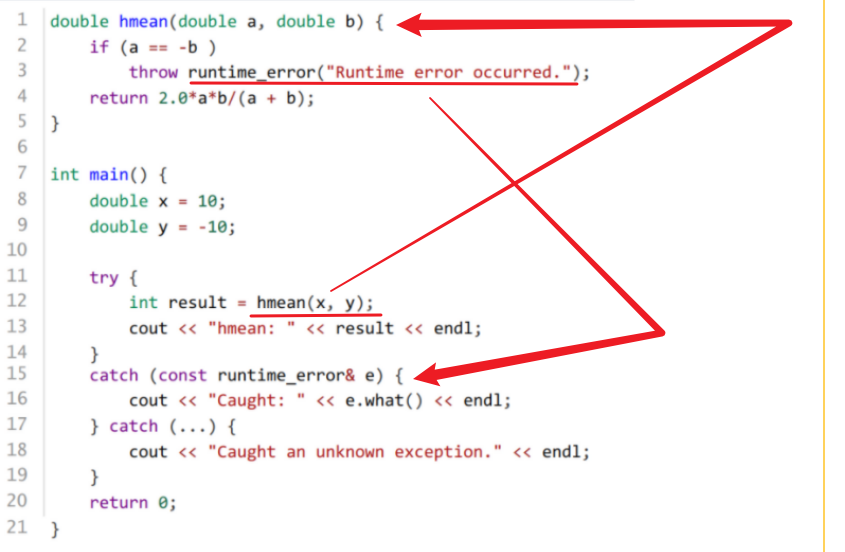
第15题
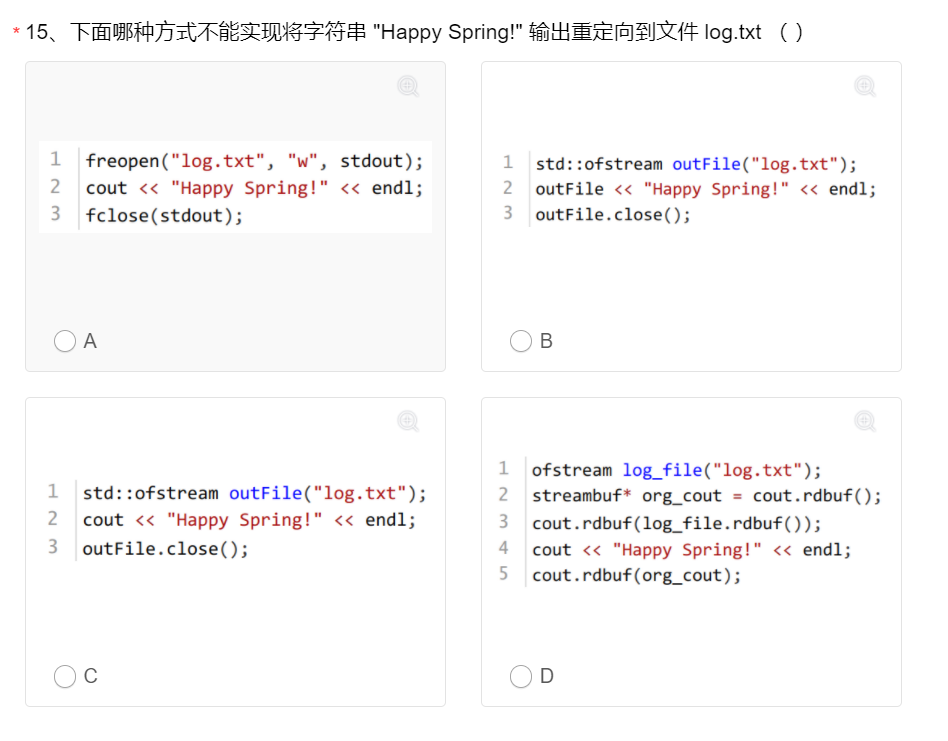
解析:
答案C,C选项应该用outFile,其他选项均对
二、判断题
第1题

解析:
答案√,函数就是这样用的
第2题

解析:
答案×,以前可以,c++11版本后就不行了,必须设置返回类型
第3题

解析:
答案√,public(外部可访问),private(外部不可访问),外部可以访问结构体

第4题

解析:
答案×,指针p的值,代表指针p指向的地址
第5题

解析:
答案√,第一个维度可以忽略
第6题

解析:
答案√,这就是递推算法的定义
第7题

解析:
答案√,T当成 " 需处理的数据 " ,即
cpp
需处理的数据T(n):需处理的数据T(n-1)+n-1(比较次数)第8题

解析:
答案×,最好的情况是O(n)
第9题

解析:
答案×,选择排序第一轮只把 "第一个位置" 和 "最小值的位置" 做交换,即 1 3 4 5 2
第10题

解析:
答案×,当一个异常被抛出(throw),但没有任何 catch 块能捕获它时,程序会自动调用 std::terminate() 函数。
三、编程题
第1题 [GESP202503 四级] 荒地开垦
题目描述
小杨有一大片荒地,可以表示为一个 n 行 m 列的网格图。
小杨想要开垦这块荒地,但荒地中一些位置存在杂物,对于一块不存在杂物的荒地,该荒地可以开垦当且仅当其上下左右四个方向相邻的格子均不存在杂物。
小杨可以选择至多一个位置,清除该位置的杂物,移除杂物后该位置变为荒地。小杨想知道在清除至多一个位置的杂物的情况下,最多能够开垦多少块荒地。
输入格式
第一行包含两个正整数 n,m,含义如题面所示。
之后 n 行,每行包含一个长度为 m 且仅包含字符 . 和 # 的字符串。如果为 .,代表该位置为荒地;如果为 #,代表该位置为杂物。
输出格式
输出一个整数,代表在清除至多一个位置的杂物的情况下,最多能够开垦的荒地块数。
输入输出样例
输入 #1
3 5
.....
.#..#
.....输出 #1
11说明/提示
样例解释
移除第二行从左数第二块空地的杂物后:
.....
....#
.....第一行从左数前 4 块荒地,第二行从左数前 3 块荒地,第三行从左数前 4 块荒地,均可开垦,4+3+4=11。
数据范围
对于全部数据,有 1 ≤ n,m ≤ 1000。
答案
cpp
#include<bits/stdc++.h>
using namespace std;
char a[1001][1001];
bool is(int x,int y){
int sum=0;
if(a[x-1][y]=='#') sum++;
if(a[x+1][y]=='#') sum++;
if(a[x][y-1]=='#') sum++;
if(a[x][y+1]=='#') sum++;
return sum==1;
}
int main() {
//1)填充数据
//1.1)确定大小n*m
int n,m;
cin>>n>>m;
//1.2)填充二维数组
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
cin>>a[i][j];
}
}
//2)计算可开垦的荒地
int ans=0,maxx=0;
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
//2.1)前提:是点点
if(a[i][j]=='.'){
//2.2)没有被杂物污染(四周围无杂物)
if( a[i-1][j]!='#' && a[i+1][j]!='#' &&a[i][j-1]!='#' &&a[i][j+1]!='#'){
ans++;
}
}else{//3)计算每个杂物的性价比,找最大
//3.1)判断四周围的点点 (是点点 && 点点周围只有一个#)
int sum=0;
if( a[i-1][j]=='.' && is(i-1,j)) sum++;
if( a[i+1][j]=='.' && is(i+1,j)) sum++;
if( a[i][j-1]=='.' && is(i,j-1)) sum++;
if( a[i][j+1]=='.' && is(i,j+1)) sum++;
//3.2)解决本身能不能被开垦
if(sum==4) sum++;
//3.3)比较找出最大值
if(maxx<sum) maxx=sum;
}
}
}
cout<<ans+maxx;
}第2题 [GESP202503 四级] 二阶矩阵
题目描述
小 A 有一个 n 行 m 列的矩阵 A。
小 A 认为一个 2×2 的矩阵 D 是好的,当且仅当 D1,1×D2,2=D1,2×D2,1。其中 Di,j 表示矩阵 D的第 i 行第 j 列的元素。
小 A 想知道 A 中有多少个好的子矩阵。
输入格式
第一行,两个正整数 n,m。
接下来 n 行,每行 m 个整数 Ai,1,Ai,2,...,Ai,m。
输出格式
一行,一个整数,表示 A 中好的子矩阵的数量。
输入输出样例
输入 #1
3 4
1 2 1 0
2 4 2 1
0 3 3 0输出 #1
2说明/提示
样例解释
样例中好的子矩阵如下:
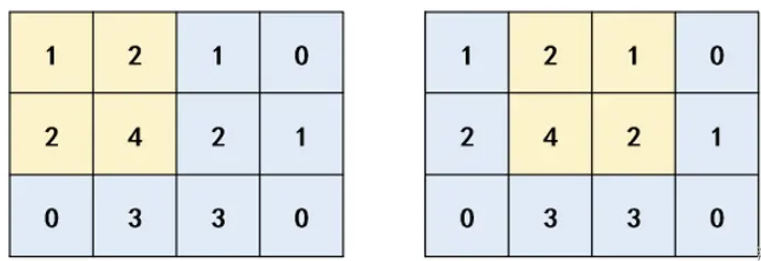
数据范围
对于所有测试点,保证 1 ≤ n ≤ 500,1 ≤ m ≤ 500,−100 ≤ Ai,j ≤ 100
答案
cpp
#include<bits/stdc++.h>
using namespace std;
int a[501][501];
int main() {
//1)填充数据
//1.1)确定大小n*m
int n,m;
cin>>n>>m;
//1.2)填充二维数组
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
cin>>a[i][j];
}
}
//2)枚举所有2*2的左顶点
//行:n-1 列:m-1
int ans=0;
for(int i=1;i<=n-1;i++){
for(int j=1;j<=m-1;j++){
//3)计算判断
//D11*D22==D12*D21
int d11=a[i][j];
int d12=a[i][j+1];
int d21=a[i+1][j];
int d22=a[i+1][j+1];
if(d11*d22==d12*d21) ans++;
}
}
cout<<ans;
}