一、WER 的定义
WER(Word Error Rate,词错误率) 是语音识别(ASR)中最常用、最基础 的评价指标,用来衡量识别结果与人工标注文本之间的差异程度 。
它本质上是一个 编辑距离(Levenshtein Distance)在"词"级别上的归一化形式。
二、WER 的定义公式
其中:
-
S(Substitution)替换错误:识别成了错误的词
-
D(Deletion)删除错误:漏识了词
-
I(Insertion)插入错误:多识别了词
-
N :参考文本(Ground Truth)中的词数
-
例如 参考文本 "SCUT" 合成文本**"SCCT"**
-
那么N=4 S=1 D=0 I =0
-
词错误率为 25%(把一个字母看作一个词,这里有点不严谨)
分子是"错误数",分母是"真实词数"
三、WER 的算法
编辑距离
编辑距离,由前苏联数学家弗拉基米尔·莱温斯坦在1965年提出,通过计算两个字符串互相转换所需要的最小编辑数来描述两个字符串的差异,编辑操作包括替换,删除,插入。编辑距离也叫莱温斯基距离,当前被广泛用于字错率计算。
S+D+I就是编辑距离。
简单记,我们只考虑编辑距离,不具体看S、D、I
计算编辑距离
首先,我们需要一个距离矩阵。
以参考文本"紫灵好看" 合成文本"宋玉更好看"为例。
首先我们添加一个填充符号NULL
然后制作这样一个表格
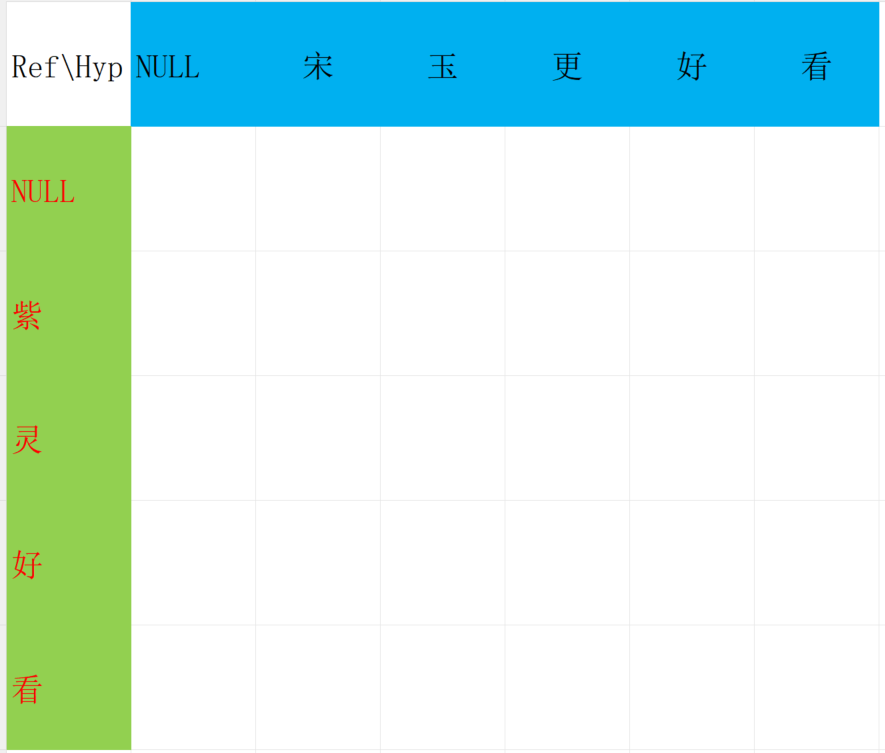
表格的意义
图片中的橙色方块表示 合成文本 "紫" 到 "宋玉" 的编辑距离。
图片中的黑色方块表示 合成文本 "紫灵好" 到 "宋玉更好" 的编辑距离。

几个共识
很明显可以填出表格以下字段
因NULL到 "宋玉" 那编辑距离就是2,相当于增加了2个字符。
其他同理。
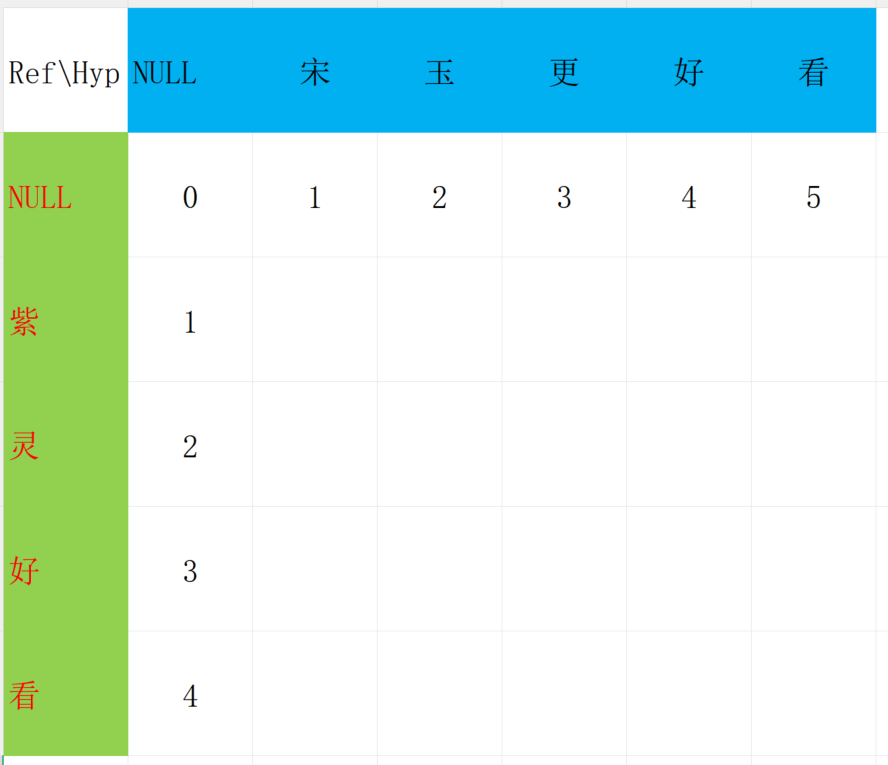
其他位置的求法
观察黑色的方块,这个方块表示 "紫"到"宋"的编辑距离。
"紫"和"宋"不相等,所以需要进行替换,距离加1。
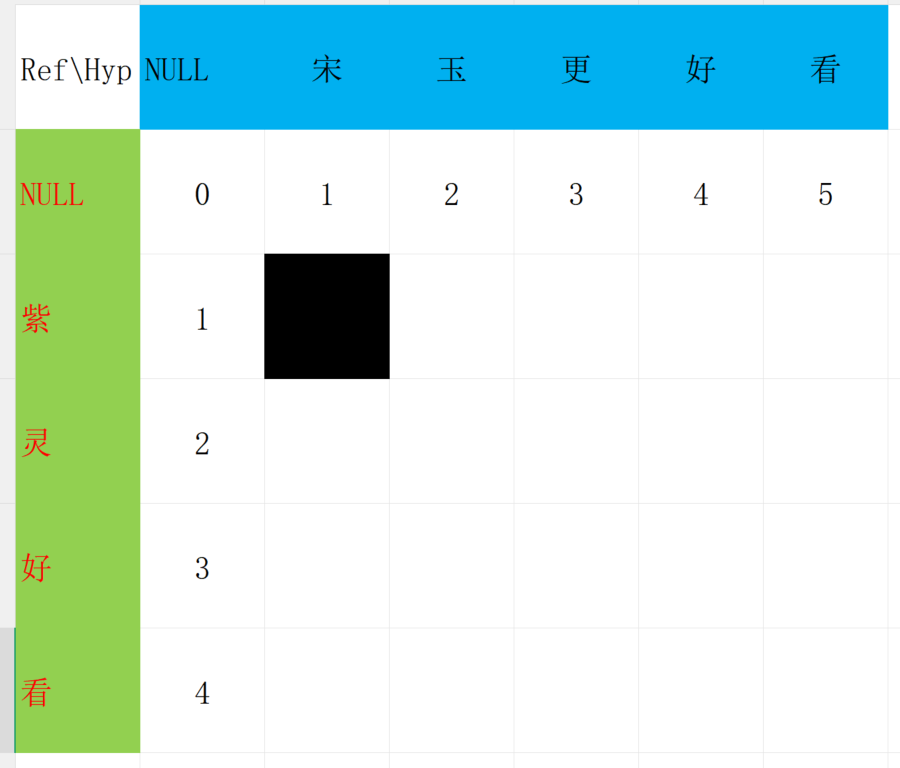
但是是在那个基础上进行加1呢?
有三种方法可以得到我们这个黑色的位置。
++黄色代表换++
++红色代表增++
++绿色代表删++
在这3种方式中选择最小的再加1
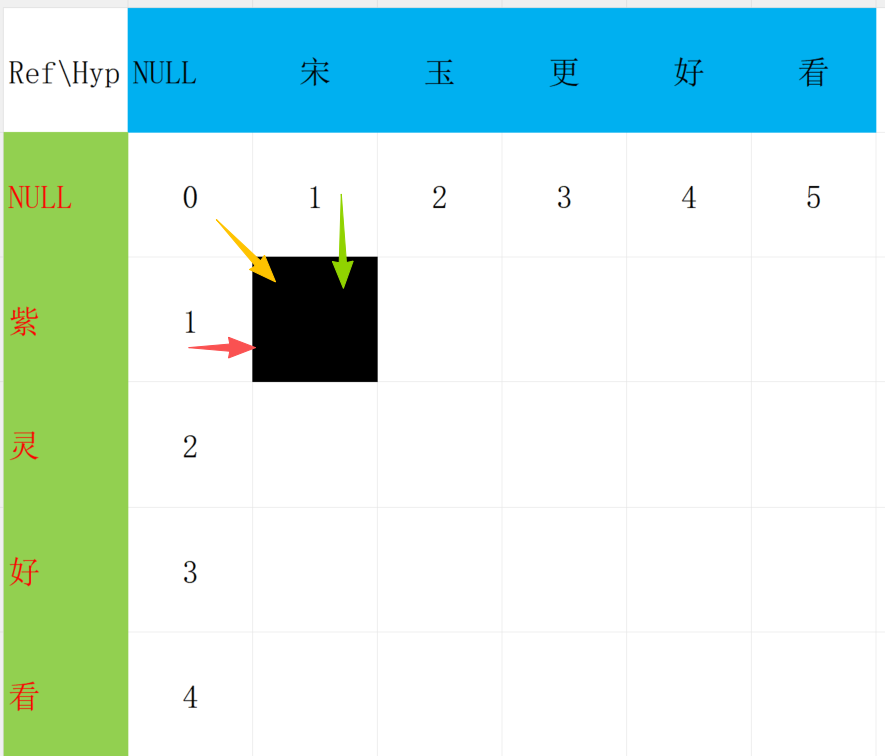
得到这一步
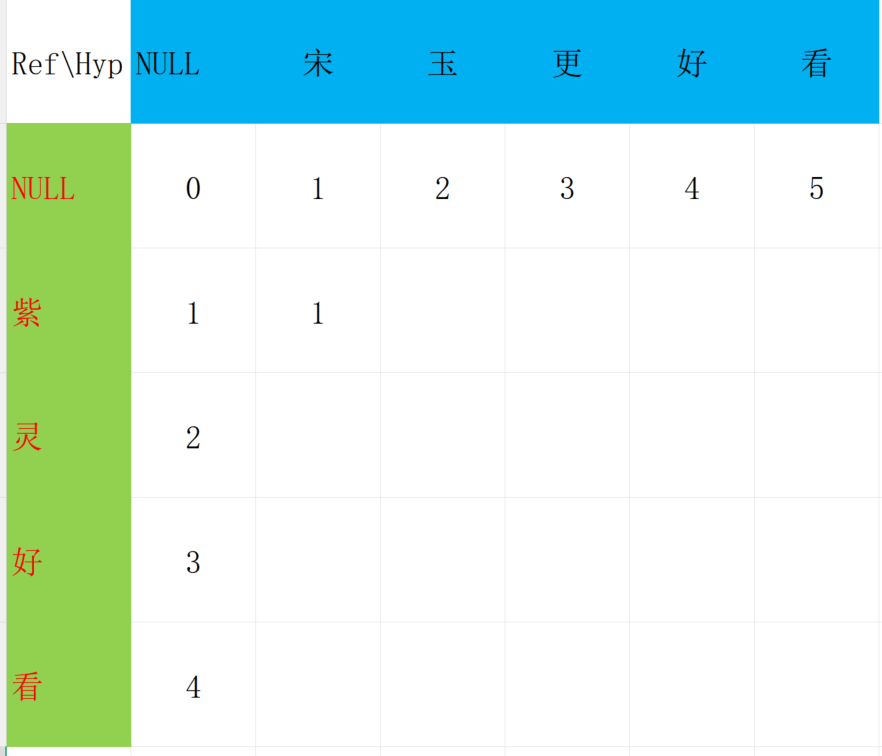
同理,我们可以继续填出其他的位置
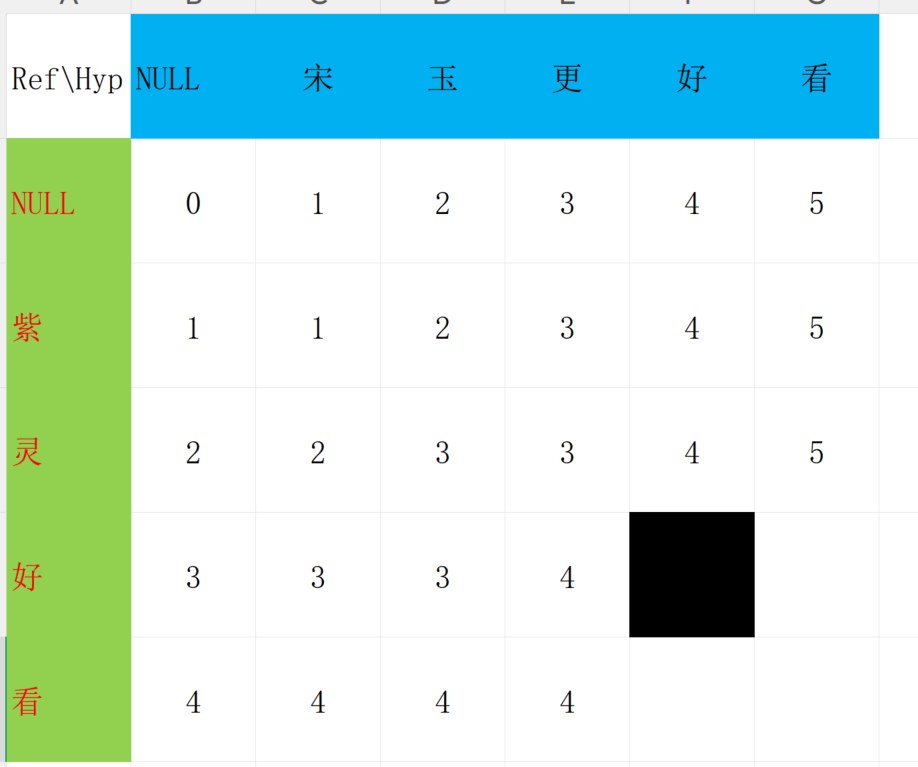
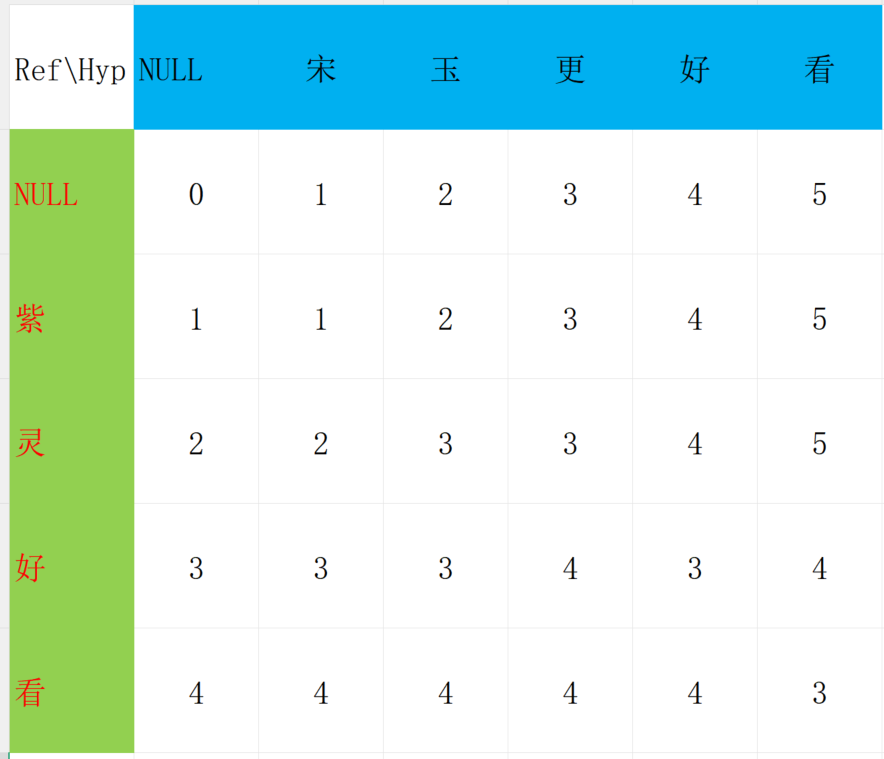
注意!此时黑色的方块它们的字是一样的!所以不需要处理,直接得到最小值就可以了!
最后的结果是经过3步就可以从合成文本变成参考文本!
WER=75%
参考代码
def wer_stats(ref: List[str], hyp: List[str]) -> Tuple[int, int, int]:
"""
计算词级编辑距离对齐,返回 (S, D, I)
ref: 参考词序列
hyp: 预测词序列
"""
n, m = len(ref), len(hyp)
# dp[i][j] = (cost, S, D, I)
dp = [[(0, 0, 0, 0) for _ in range(m + 1)] for _ in range(n + 1)]
# 初始化:ref -> 空:全是删除
for i in range(1, n + 1):
cost, s_cnt, d_cnt, i_cnt = dp[i - 1][0]
dp[i][0] = (cost + 1, s_cnt, d_cnt + 1, i_cnt)
# 初始化:空 -> hyp:全是插入
for j in range(1, m + 1):
cost, s_cnt, d_cnt, i_cnt = dp[0][j - 1]
dp[0][j] = (cost + 1, s_cnt, d_cnt, i_cnt + 1)
for i in range(1, n + 1):
for j in range(1, m + 1):
if ref[i - 1] == hyp[j - 1]:
dp[i][j] = dp[i - 1][j - 1]
else:
# substitute
c1, s1, d1, i1 = dp[i - 1][j - 1]
sub = (c1 + 1, s1 + 1, d1, i1)
# delete
c2, s2, d2, i2 = dp[i - 1][j]
dele = (c2 + 1, s2, d2 + 1, i2)
# insert
c3, s3, d3, i3 = dp[i][j - 1]
ins = (c3 + 1, s3, d3, i3 + 1)
# 选 cost 最小;若相同,偏向更少 S 再少 D 再少 I(可改)
dp[i][j] = min([sub, dele, ins], key=lambda x: (x[0], x[1], x[2], x[3]))
_, S, D, I = dp[n][m]
return S, D, I