数据结构基础：B树磁盘IO优化的数据结构艺术

1、B树的起源

B树（B-Tree）是由Rudolf Bayer和Ed McCreight在1972年发明的一种自平衡的搜索树。注意：B树中的"B"可能代表"Balanced"（平衡）或者发明者"Bayer"的名字，名字不重要，但更重要的是理解它的特性。

在讨论B树之前，我们先来思考一个问题：现有的数据结构（如二叉搜索树）有什么局限性？

在计算机的世界里，数据结构的选择往往取决于存储介质的特性。我们熟悉的二叉搜索树、AVL树等，都是为在内存中进行高效查找而设计的。当数据量非常大时，我们无法将所有数据存储在内存中，必须存储在磁盘上。而磁盘访问速度比内存慢数千倍！在处理存储于磁盘上的海量数据时，这些"内存友好"的结构就显得力不从心了。

核心矛盾：内存 vs. 磁盘

速度差异： 内存（RAM）的访问速度是纳秒级别的，而机械硬盘（HDD）的访问速度是毫秒级别的。两者之间存在着数万甚至数十万倍的差距。CPU在等待磁盘IO时，几乎处于完全空闲的状态。
**读取方式：**磁盘读取数据不是按字节读取，而是以"块"或"页"为单位进行的，通常一个块的大小是4KB或更大。这意味着，即使你只需要1个字节的数据，操作系统也会从磁盘读取至少4KB的内容到内存中。

想象一下，如果我们在磁盘上用一个普通的二叉搜索树来存储数百万条记录。树会变得非常"高瘦"。

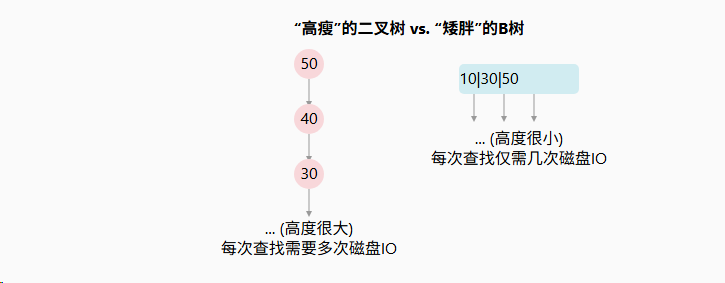
查找一个数据，可能需要从根节点一路向下访问很多层。每一层节点都存储在不同的磁盘块上，这意味着一次查询可能引发数十次甚至更多的磁盘IO。这是无法接受的性能瓶颈。

B树的设计哲学

为了解决这个问题，B树（B-Tree，不要误读为B减树）应运而生。它的核心思想非常直接：

既然磁盘IO很昂贵，那就尽可能减少IO次数。
既然磁盘一次会读取一整块，那就让每个节点尽可能地大，充分利用这块空间。

B树通过构建一棵"矮胖"的树，完美地实践了这一哲学。它的每个节点可以存储大量的关键字和指向子节点的指针。这样一来，树的高度被极大地压缩，从根节点到任何叶子节点的路径都非常短，从而显著减少了磁盘IO的次数。

2、B树的核心特性

一个B树由它的阶数（Order） 定义，通常用字母 m表示。一个 m 阶的B树是一棵平衡的多路搜索树。

为了让概念更具体，我们可以把整个B树想象成一个图书馆为了快速找书而设计的索引系统。

磁盘块： 图书馆里的一个大索引柜的抽屉。每次找书，图书管理员（CPU）最耗时的操作就是拉开一个沉重的抽屉（磁盘IO）。
B树节点: 抽屉里的一张大索引卡片。我们的目标是让这张卡片上写满信息，这样拉开一次抽屉就能看到很多指引，不用频繁地开合不同抽屉。
阶数 m: 规定了每张索引卡片上最多能写多少个"索引条目"（关键字）。阶数越大，卡片越大，能写的条目就越多。
关键字: 索引卡片上的一个"索引条目"，比如"计算机科学: H-K"。它告诉你，书名首字母在H到K之间的书，应该去哪个子区域找。
子节点指针: 索引条目旁边的一个指示箭头，告诉你下一步该去查阅哪一张更具体的索引卡片（下一个节点）。

B树的设计目标就是：让每张索引卡片（节点）尽可能大（充分利用磁盘块），从而让整个索引系统的层级（树的高度）变得非常少。这样，从第一张总索引卡片（根节点）查到任何一本书的位置，都只需要翻阅极少数几张卡片（几次磁盘IO）。

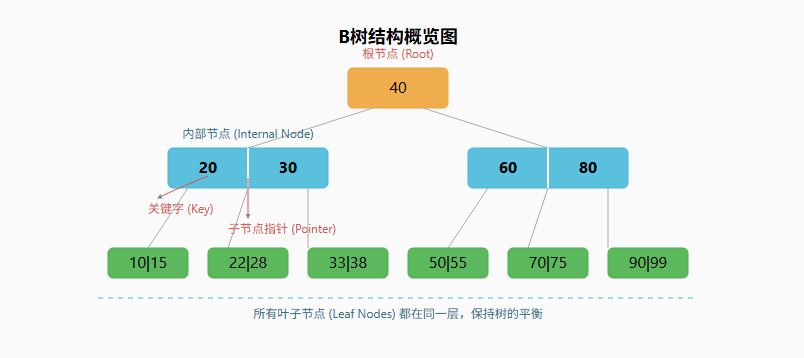
2.1、阶数

阶数 m 定义了树中一个节点最多能拥有的子节点数量。它决定了B树的"胖瘦"。m 越大，节点能存储的关键字越多，树也就越"胖"，高度越低。

2.2、节点结构

每个节点都包含两部分信息：

关键字： 节点内按升序排列的关键字。例如 [10, 25, 40]。
子节点指针： 指向其子节点的引用。

一个包含 k 个关键字的内部节点（非叶子节点）将会有 k+1个子节点指针。这些指针将关键字划分开区间。

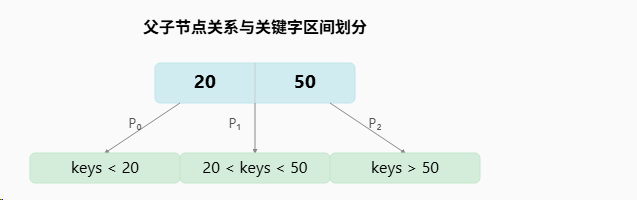
父节点的关键字就像"路牌"，把数据划分到不同的区间。要查找 35，因为 20 < 35 < 50，所以会沿着 P₁ 指针去中间的子节点继续查找。

2.3、核心规则（m阶B树）

关键字数量：
- 根节点：最少有 1 个关键字，最多有 m-1个关键字。
- 非根节点：最少有 ⌈m/2⌉ - 1 个关键字，最多有 m-1 个关键字。
子节点数量：
- 根节点：最少有 2 个子节点（除非树只有一个节点），最多有 m 个子节点。
- 非根内部节点：最少有 ⌈m/2⌉ 个子节点，最多有 m 个子节点。
关键字排序 ：节点内的关键字按升序排列：K₁ < K₂ < ... < K_k
子树规则 ：
- 对于任意关键字K_i，其左子树中的所有关键字都小于 K_i
- 其右子树中的所有关键字都大于 K_i
关键字范围（搜索树性质）： 对于任何一个内部节点，如果其关键字为 [K₁, K₂, ..., Kₖ]，它将有 k+1 个子节点指针 [P₀, P₁, ..., Pₖ]。这些指针所指向的子树中的关键字范围被严格限定：
- P₀ 指向的子树中所有关键字都 **小于K₁。
- 对于 1 ≤ i < k，Pᵢ 指向的子树中所有关键字都介于 Kᵢ 和 Kᵢ₊₁ 之间。
- Pₖ 指向的子树中所有关键字都 **大于 Kₖ。
这个规则是B树能够进行高效查找的基础，保证了查找路径的唯一性。
平衡性： 所有的叶子节点都必须在同一层。这保证了树的平衡，使得从根到任何叶子的路径长度都相同。

:::warning
为什么要有"最少关键字/子节点"的限制？

这个限制是B树能够保持平衡、避免退化成"高瘦"形态的关键。

如果不规定最少关键字数量，B树可能会退化：

极端情况：每个节点只有1个关键字 → 退化成二叉树
失去优势：树的高度增加，磁盘I/O次数增多
性能下降：失去了B树的核心优势

通过规定最少关键字数量为⌈m/2⌉-1，确保每个节点至少"半满"，从而保证树的高度始终保持在较低水平，维持O(log n)的性能保证。

:::

2.4、示例

下面是一个5阶 (m=5) B树示例

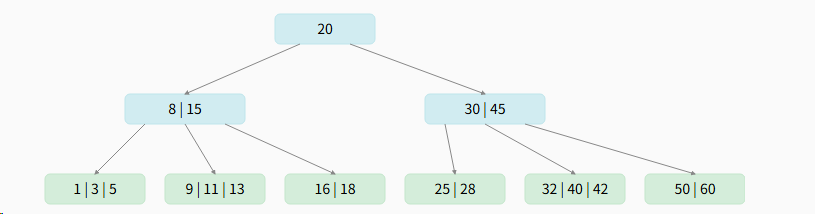
结构分析

5阶意味着 ：
- 每个节点最多4个关键字（m-1 = 5-1 = 4）
- 每个节点最多5个子节点
- 每个节点最少2个关键字（⌈5/2⌉-1 = 3-1 = 2），根节点除外
- 每个节点最少3个子节点（⌈5/2⌉ = 3），根节点和叶子节点除外
为什么所有叶子节点在同一层？
- 这是B树的核心性质之一：平衡性
- 保证所有查找操作的时间复杂度都是O(log n)

3、B树的核心操作

B树的魅力在于它能够在插入和删除操作后，通过一系列精巧的调整（分裂和合并）来自动维持平衡。

3.1、查找操作

查找操作是B树最基本也是最常用的操作。它的过程类似于在多级索引中导航，目标是利用B树"矮胖"的特性，用最少的磁盘读取次数定位到数据。

查找的基本步骤如下：

从根节点开始： 每次查找都从树的根节点启动。这会引发第一次磁盘I/O，将根节点读入内存。
节点内查找： 在当前节点的关键字列表中，使用二分查找（或线性查找）来确定目标关键字 K 的位置。
- 情况1：找到了！ 如果在当前节点中直接找到了关键字 K，查找成功结束。
- 情况2：未找到，但在区间内。 如果未找到 K，则确定 K 应该属于哪个子节点的范围。例如，如果 K 介于关键字 Kᵢ 和 Kᵢ₊₁ 之间，那么下一步就应该去访问它们中间的那个子节点指针 Pᵢ₊₁ 所指向的节点。
递归向下： 顺着上一步确定的指针，移动到下一个子节点。这会引发下一次磁盘I/O。然后，在这个新加载的节点上重复步骤2。
结束条件： 重复以上过程，直到在某个节点中成功找到关键字，或者到达了叶子节点但仍然没有找到（这意味着该关键字在树中不存在）。

核心：用内存计算换取磁盘I/O

B树查找的精髓在于，每加载一个节点到内存（一次昂贵的磁盘I/O），就在内存中进行一系列"廉价"的比较操作，以确保下一步的磁盘I/O是绝对必要的，并且方向是完全正确的。整个过程就是用多次内存中的快速计算，来替代多次磁盘上的慢速寻道和读取。

示例：在下面的5阶B树中查找关键字 42

步骤 1：检查根节点

第一次磁盘 I/O, 读取根节点 [20] 到内存。
在内存中比较：因为 42 > 20, 所以选择右侧指针继续查找。

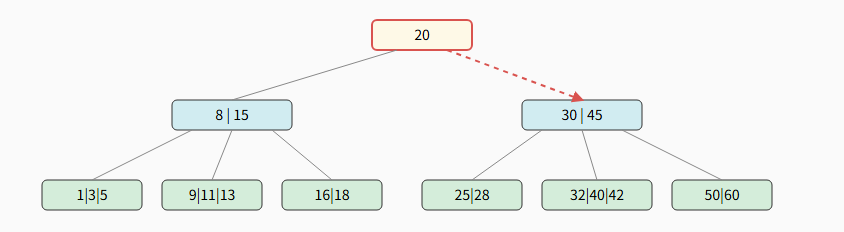
步骤 2：检查内部节点

第二次磁盘 I/O, 读取节点 [30 | 45] 到内存。
在内存中比较：因为 30 < 42 < 45, 所以选择中间指针。

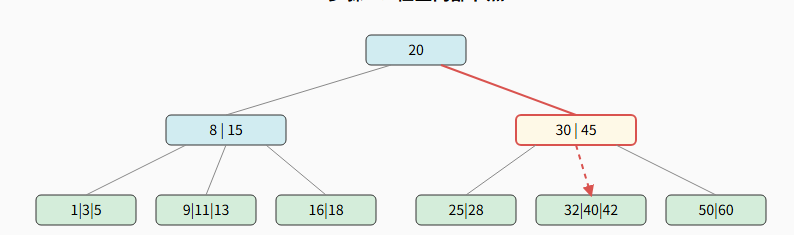
步骤 3：在叶子节点找到目标

第三次磁盘 I/O, 读取叶子节点 [32 | 40 | 42] 到内存。
在节点内找到关键字 42。查找成功！总 I/O 次数: 3。

:::info
内存中的快速查找

一旦节点被读入内存，在节点内查找关键字非常快：

小数组：每个节点通常只有几十个关键字
二分查找：可以使用二分查找，时间O(log k)，k是节点内关键字数
内存速度：内存访问速度是纳秒级别，可以忽略不计
关键瓶颈 ：真正耗时的是磁盘I/O，而不是内存中的查找

:::

3.2、插入操作

插入是B树最核心的操作之一。B树的插入比查找复杂得多，因为需要维护B树的性质。B树总是将新关键字插入到叶子节点中。

:::info
为什么B树总是将新关键字插入到叶子节点中？

这是一个非常深刻的问题，触及了B树设计的核心原则。简单来说，这是为了用最简单、最统一的方式来维持树的平衡和有序性。

试想一下，如果允许插入到内部节点，会带来巨大的复杂性：当一个新关键字被插入内部节点时，它会改变该节点的区间划分，那么原有的子节点指针和它们所代表的庞大子树就需要被复杂地拆分和重新分配。这是一种代价极高且难以实现的操作。

假设我们要把关键字 35 插入到下面这个内部节点 [20 | 50] 中：

... [父节点] ...

复制代码

        |

  [20 | 50]  <-- 想在这里插入 35

 /    |    \

... ... ...

(<20) (20-50) (>50)

如果我们将 35 直接插入，节点会变成 [20 | 35 | 50]。现在问题来了：

子节点指针怎么办？ 原来这个节点有3个子节点指针，分别指向"小于20"、"20到50之间"、"大于50"的子树。现在我们有4个区间了（"<20", "20-35", "35-50", ">50"），所以需要4个子节点指针。多出来的那个指针该指向哪里？
子树如何处理？ 原来"20到50之间"的那个子树，现在必须被分裂成两个子树："20到35之间"和"35到50之间"。这是一个极其复杂且代价高昂的操作，可能需要递归地向下修改很多节点，完全违背了B树高效的初衷。

因此，B树规定所有插入都必须在"终点"------叶子节点进行，这带来了三大好处：

**定位简单：**任何要插入的关键字，总能通过查找操作定位到一个唯一的叶子节点。
**结构清晰：**在叶子节点插入不会影响其下方的任何结构，因为它没有子节点。
**平衡机制统一：**插入后唯一可能出现的问题就是叶子节点"上溢"（满了），而B树对此有统一的解决方案------"节点分裂"，然后将中间值"提拔"到父节点。这是B树向上生长并保持平衡的唯一方式，逻辑清晰且高效。

插入的算法主要步骤：

定位： 首先，像查找操作一样，找到应该插入新关键字的那个叶子节点。
插入： 将新关键字插入到该叶子节点的正确位置，保持节点内关键字有序。
调整（关键步骤）：
- 情况1：节点未满。 如果插入后，该叶子节点的关键字数量没有超过 m-1，操作结束。这是最简单的情况。
- 情况2：节点已满（上溢 Overflow）。 如果插入后，节点关键字数量达到 m，则必须进行分裂操作来维持B树的性质。

3.2.1、核心操作：节点分裂

当向一个已满的节点 （含有m-1个关键字）插入新关键字时，节点会有m个关键字， 超过了B树的限制 。这时必须进行分裂操作来维护B树的性质。

那么为什么不能简单地扩大节点容量？

保持平衡的必要性

磁盘块大小限制：每个节点对应一个磁盘块，磁盘块大小是固定的（通常4KB或8KB）
保持树的平衡：如果允许节点任意大，树会变得不平衡，失去性能优势
统一的性能保证：通过限制节点大小，确保所有操作都是O(log n)时间复杂度

分裂操作原理：

当一个节点上溢时，B树通过"向上生长"来解决问题：

从 m 个关键字中选取中间的一个关键字。
将这个中间关键字提升到其父节点中。
以中间关键字为界，将原节点分裂成左右两个新节点。
如果父节点因为接收了提升的关键字也满了，则对父节点重复分裂操作。这个过程可能一直递归到根节点。如果根节点也分裂了，树的高度就会增加1。这是B树高度增加的唯一方式。

如何确定分裂时的"中间值"？

当一个节点因为插入而"上溢"时，它会临时包含 m 个关键字。选择哪个关键字作为"中间值"提升到父节点是有固定规则的。这个规则保证了分裂后产生的两个新节点都满足B树的最小关键字数量要求。

规则： 在一个包含 m 个关键字（索引从 0 到 m-1）的临时上溢节点中，我们选择索引为⌈m/2⌉ - 1的关键字作为中间值。

示例 1：奇数阶 (m=5)

临时上溢节点有 5 个关键字。
中间值索引 = ⌈5/2⌉ - 1 = 3 - 1 =2。
所以，索引为2的关键字被提升。

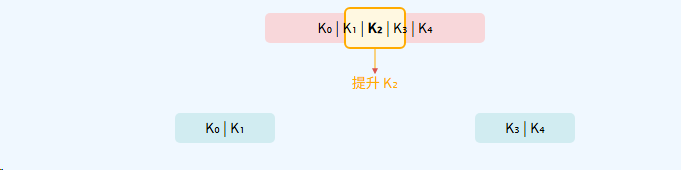
示例 2：偶数阶 (m=6)

临时上溢节点有 6 个关键字。
中间值索引 = ⌈6/2⌉ - 1 = 3 - 1 =2。
所以，索引为2的关键字被提升。分裂后左节点2个key，右节点3个key，都满足规则。

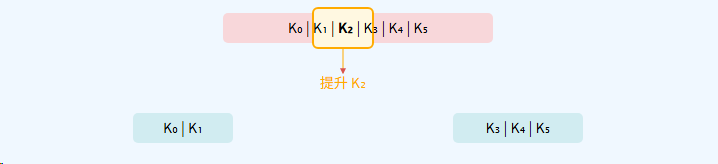
3.2.2、示例1：简单插入（节点未满）

我们将在下面的5阶B树中插入关键字 26。在一个5阶树中，节点最多可以有4个关键字。

步骤 1: 定位到目标叶子节点

26 > 20, 走右指针。
26 < 30, 走左指针, 定位到叶子节点 [25 | 28]。

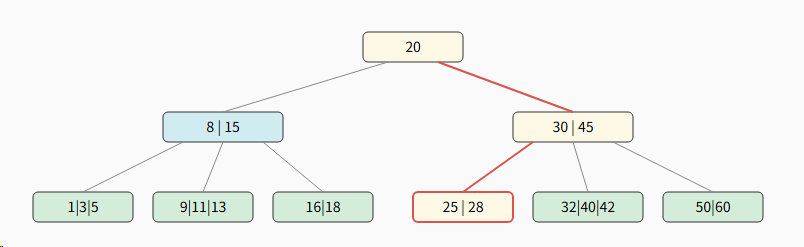
步骤 2: 插入并完成

3.2.3、示例2：复杂插入（节点分裂）

现在，我们来看一个更复杂的情况：插入关键字 19。这次插入将导致叶子节点上溢，从而触发分裂和提升操作。

步骤 1: 定位目标叶子节点初始树状态

初始树状态 (5阶)，目标叶子节点 [18 | 20 | 22 | 24] 已满。

19 < 30, 走左指针。
15 < 19 < 25, 走中间指针, 定位到叶子节点 [18 | 20 | 22 | 24]。

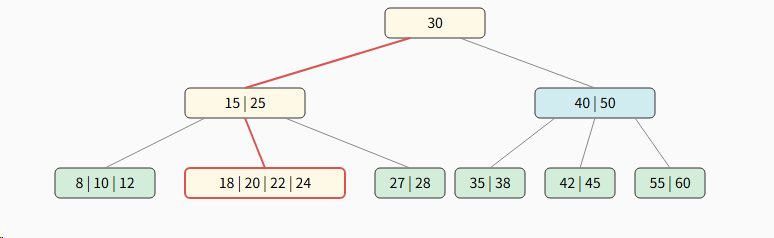
步骤 2: 临时插入导致上溢

节点上溢！(包含5个关键字, 超过m-1=4的限制)必须进行分裂操作。

步骤 3: 找到中间值并分裂

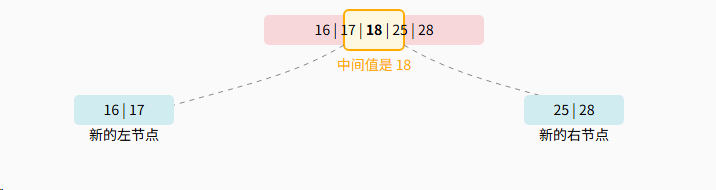
步骤 4: 提升中间值，完成插入

中间值 20 被提升到父节点 [15 | 25] 中，最终树的状态如下。

父节点接收 20 后变为 [15 | 20 | 25]，未满，操作结束。。

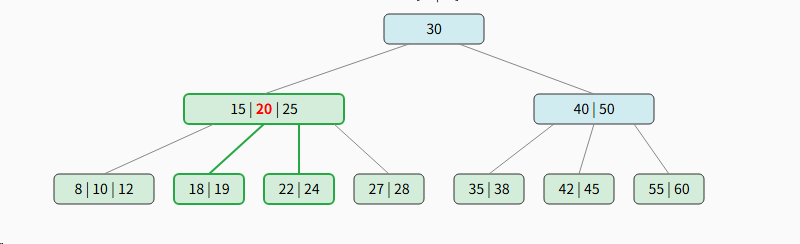
3.3、删除操作

删除操作比插入更复杂，因为它需要处理下溢的情况，即删除后节点关键字数量少于 ⌈m/2⌉ - 1。

删除的基本步骤：

定位关键字： 从根节点开始，查找到包含目标关键字 K 的节点 N。
执行删除：
- 情况 A：K 在叶子节点 N****中。这是最直接的情况，直接从 N 中删除 K。
- 情况 B：K 在内部节点 N****中。此时不能直接删除，因为会破坏子树的结构。我们需要：
  1. 找到 K 的前驱或后继。前驱是 K 左子树中的最大关键字，后继是 K 右子树中的最小关键字。它们必定存在于叶子节点中。
  2. 用前驱（或后继）的值替换 N 中的 K。
  3. 现在，问题转化为删除那个作为前驱（或后继）的关键字，它位于一个叶子节点中。这就回到了情况 A。
修复下溢（如果发生）： 在从叶子节点删除一个关键字后，检查该节点是否发生下溢。如果发生下溢，必须进行修复：
- 策略1：从兄弟节点"借用" - 优先选择。 如果下溢节点的直接左兄弟或右兄弟有多余的关键字（数量 > 最小值），可以从它那里"借"一个。这个过程需要通过父节点中转，以维持排序。这叫做旋转。
- 策略2：与兄弟节点"合并"。 如果相邻的兄弟节点也处于"最低温饱线"，都没有多余的关键字可借，那么就必须进行合并。合并会将下溢节点、一个兄弟节点以及它们在父节点中的分隔关键字合并成一个新节点。

为什么删除这么复杂，既要借用又要合并？

这都是为了严格维持B树的"最少关键字数量"的规则。如果删除了一个关键字就任由节点下溢，树的平衡性就会被打破，查询效率会下降。

**优先借用：**借用（旋转）对树的结构改变更小，只需要移动几个关键字，比合并更高效。所以总是优先尝试借用。
**万不得已才合并：**只有当兄弟节点也"自身难保"时，才选择合并。合并是一个更大的结构调整，它可能会导致父节点也发生下溢，从而需要递归地向上进行合并，最坏情况下可能导致树的高度降低1。

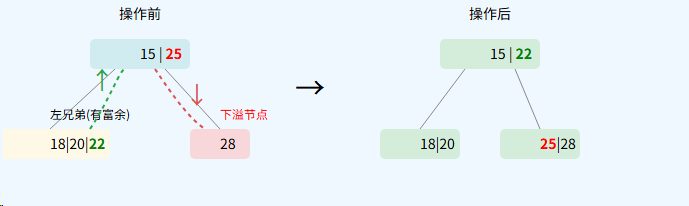
借用规则（旋转）

条件： 当下溢节点的直接左兄弟或右兄弟有多余的关键字（即关键字数量 > ⌈m/2⌉ - 1）时，可以执行借用操作。

从左兄弟借用：父节点中 紧邻的右侧分隔关键字"下沉"到下溢节点的最左边，左兄弟的最大关键字"上提"到父节点，替换掉下沉的关键字。
从右兄弟借用：父节点中 紧邻的左侧分隔关键字"下沉"到下溢节点的最右边，右兄弟的最小关键字"上提"到父节点，替换掉下沉的关键字。

简而言之： "父下，兄上"

合并规则

条件： 当下溢节点的所有直接兄弟都只包含最小数量的关键字，无法借用时，必须执行合并操作。

过程： 将**[下溢节点]** +[父节点分隔关键字] +**[相邻兄弟节点]**这三部分合并成一个新节点。

简而言之: "三合一"

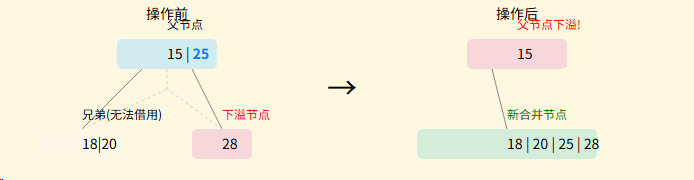
**重要后果：**合并操作会从父节点中移除一个关键字，这可能导致父节点也发生下溢。如果发生这种情况，修复过程将以同样的方式（先尝试借用，再尝试合并）在父节点上递归进行，一路向上传递，直到根节点。如果根节点也被合并变空，树的高度就会降低1。

下面用几个示例来看一下完整的删除过程

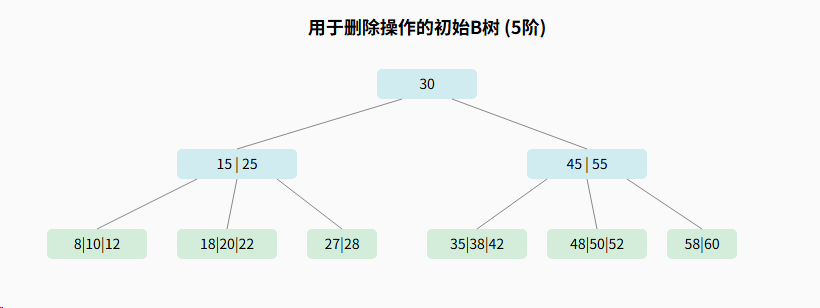
3.3.1、示例1：简单删除（从叶子节点删除，不导致下溢）

我们将在下面的5阶B树（最小关键字数为2）中删除叶子节点中的关键字 12。

删除前: 目标节点 [8 | 10 | 12] 包含3个关键字

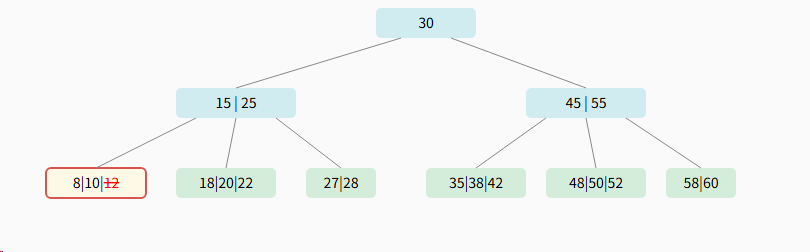
删除后: 节点 [8| 10] 仍有2个关键字，满足规则，无需调整，删除完成。

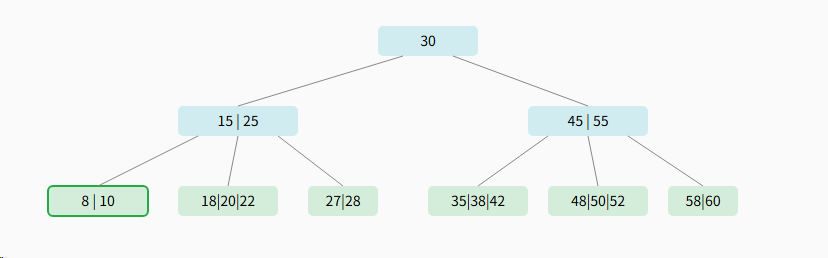
3.3.2、示例2：复杂删除（从内部节点删除）

我们将删除内部节点中的关键字 15。我们需要用它的前驱或后继来替换它。

步骤 1: 定位内部节点中的 15并找到其前驱

关键字 15 的前驱是其左子树中的最大值，即 12。

下一步: 用 12 替换 15，然后删除叶子节点中的 12

步骤 2: 完成替换与删除

删除叶子节点中的 12 后，节点 [8|10] 仍满足要求，操作完成。

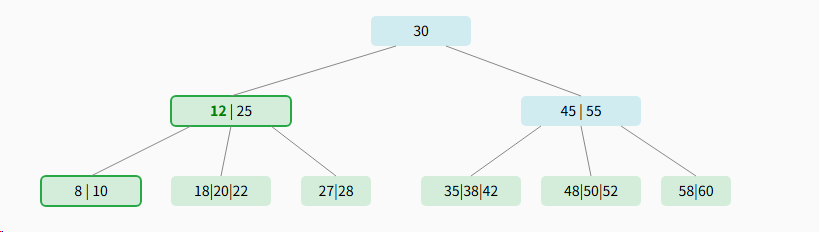
3.3.3、示例3：修复下溢（借用操作）

我们将删除关键字 27，删除后，剩余节点 [28] 发生下溢。我们需要修复它。5阶B树的最小关键字数是2。

步骤 1: 检查兄弟节点是否可以"借用"

下溢节点 [27] 的左兄弟是 [18 | 20 | 22]，它有3个关键字（> 最小值2）。

因此，可以从左兄弟处"借用"，进行旋转操作。

步骤 2: 执行旋转操作

1.父节点的分隔key(25)下放。

2.兄弟节点的最大key(22)上提。

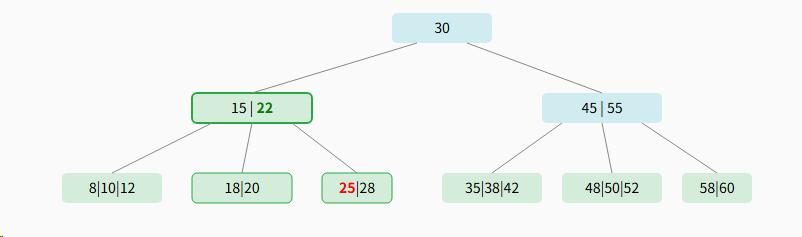
3.3.4、示例4：修复下溢（合并操作）

现在，我们来看一个必须进行合并的场景。我们将先删除 22 ，再删除 27，这将触发一次合并，并导致父节点下溢，从而引发一次递归的向上合并，最终导致树的高度降低。

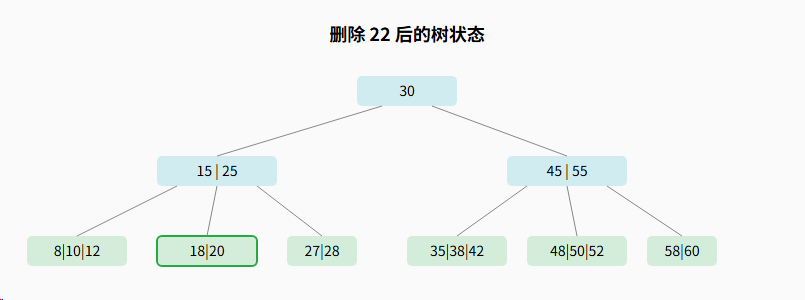
步骤 1: 删除 27 导致下溢，且兄弟无法借用

删除 27 后，节点 [28] 只剩1个关键字，少于最小值2，发生下溢。

步骤 2: 检查兄弟节点，发现无法借用

下溢节点的右兄弟 [18 | 20] 只有2个关键字，已是最小值，无法出借。

因此，必须进行合并操作。

步骤 3: 执行合并操作

兄弟[18|20] + 父分隔符(25) + 下溢节点[28]

父节点 [15|25] 中的 25 被拉下合并后，变为 [15]，触发了新的下溢！

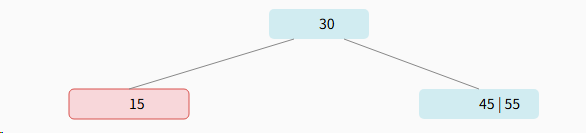
步骤 4: 递归修复父节点的下溢

节点 [15] 下溢，且其兄弟 [45|55]无法出借，因此需要再次合并。下溢节点[15] + 父分隔符(30) + 兄弟[45|55]

最终的B树结构

原根节点合并后消失，树的高度降低了 1。

4、Python实现B树

在B树的代码实现中，经常看到两个关键参数：阶数 (Order, m) 和最小度数 (Minimum Degree, t)。虽然它们描述的是同一棵树，但出发点不同，这在代码实现中尤为重要。

阶数 (m) ：定义了一个节点最多能有多少个子节点。这是从"上限"来描述B树。例如，一个5阶B树的节点最多有5个孩子。
最小度数 (t) ：定义了一个非根节点最少能有多少个子节点 。这是从"下限"来描述B树，是维持B树"矮胖"特性的核心。t >= 2。

在许多算法教材（如《算法导论》）和代码实现中，更倾向于使用 t 作为基本参数，因为B树的所有平衡操作（分裂和合并）都围绕着维持"最小数量"这个下限来展开。使用 t 可以让算法逻辑变得非常优雅和对称。

它们的关系：m = 2 * t。一个阶数为 m 的B树，其最小度数 t 为 m/2。反之，一个最小度数为 t 的B树，其阶数 m 为 2t。

基于最小度数(t)的性质详解

一旦我们确定了最小度数 t，B树的所有其他限制都可以由此推导出来：

min_children = t(最小子节点数，根节点除外)
这正是 t 的定义。这个规则确保了每个节点至少有 t 个分支，防止树变得过于稀疏。
min_keys = t - 1(最小关键字数，根节点除外)
因为一个有 k 个关键字的节点总是有 k+1 个子节点。所以，当子节点数量最少为 t 时，关键字数量自然最少为 t - 1。
max_keys = 2 * t - 1(最大关键字数)
这是B树分裂机制的关键。一个节点被设计成在达到 2t-1 个关键字时"满载"。当试图插入第 2t 个关键字时，节点会发生分裂：中间的那个关键字（第 t 个，索引为 t-1）被"提升"到父节点，剩下的 2t-2 个关键字正好可以平分给两个新的子节点，每个子节点分到 t-1 个关键字------这恰好是B树节点的最小关键字数！这种设计使得分裂操作非常干净利落。
max_children = 2 * t(最大子节点数)
当一个节点达到最大关键字数 2t-1 时，它拥有的子节点数就是 (2t - 1) + 1 = 2t。这也就是B树的"阶数"m。

总结： 用 t 来定义B树，使得"满"和"半满"状态的转换在数学上完美对称，极大地方便了代码实现。

下面是一个B树实现，包含查找、插入、删除等核心操作。

python 复制代码

#!/usr/bin/env python3
# -*- coding: utf-8 -*-


class BTreeNode:
    """B树节点类"""
    
    def __init__(self, leaf=True):
        """
        初始化节点
        
        参数:
            leaf: 是否为叶子节点
        """
        self.keys = []  # 关键字列表
        self.children = []  # 子节点指针列表
        self.leaf = leaf  # 是否为叶子节点
    
    def __str__(self):
        return f"Keys: {self.keys}, Leaf: {self.leaf}, Children: {len(self.children)}"


class BTree:
    """B树类"""
    
    def __init__(self, t):
        """
        初始化B树
        
        参数:
            t: 最小度数(minimum degree)
               - 每个节点最多 2t-1 个关键字
               - 每个节点最少 t-1 个关键字(根节点除外)
               - 每个节点最多 2t 个子节点
               - 每个节点最少 t 个子节点(根节点和叶子节点除外)
        """
        self.root = BTreeNode(True)
        self.t = t
    
    def search(self, key, node=None):
        """
        在B树中查找关键字
        
        参数:
            key: 要查找的关键字
            node: 从哪个节点开始查找(默认从根节点)
        
        返回:
            (节点, 索引) 如果找到
            None 如果未找到
        """
        if node is None:
            node = self.root
        
        # 在当前节点中查找关键字的位置
        i = 0
        while i < len(node.keys) and key > node.keys[i]:
            i += 1
        
        # 如果找到关键字
        if i < len(node.keys) and key == node.keys[i]:
            return (node, i)
        
        # 如果是叶子节点且未找到
        if node.leaf:
            return None
        
        # 递归在子节点中查找
        return self.search(key, node.children[i])
    
    def insert(self, key):
        """
        在B树中插入关键字
        
        参数:
            key: 要插入的关键字
        """
        root = self.root
        
        # 如果根节点已满，需要分裂
        if len(root.keys) == (2 * self.t) - 1:
            # 创建新的根节点
            new_root = BTreeNode(False)
            new_root.children.append(self.root)
            
            # 分裂原来的根节点
            self._split_child(new_root, 0)
            self.root = new_root
            
            # 在新根节点中插入关键字
            self._insert_non_full(new_root, key)
        else:
            self._insert_non_full(root, key)
    
    def _insert_non_full(self, node, key):
        """
        在未满的节点中插入关键字
        
        参数:
            node: 未满的节点
            key: 要插入的关键字
        """
        i = len(node.keys) - 1
        
        if node.leaf:
            # 在叶子节点中插入关键字
            node.keys.append(None)
            while i >= 0 and key < node.keys[i]:
                node.keys[i + 1] = node.keys[i]
                i -= 1
            node.keys[i + 1] = key
        else:
            # 找到应该插入的子节点
            while i >= 0 and key < node.keys[i]:
                i -= 1
            i += 1
            
            # 如果子节点已满，先分裂
            if len(node.children[i].keys) == (2 * self.t) - 1:
                self._split_child(node, i)
                if key > node.keys[i]:
                    i += 1
            
            self._insert_non_full(node.children[i], key)
    
    def _split_child(self, parent, index):
        """
        分裂子节点
        
        参数:
            parent: 父节点
            index: 要分裂的子节点在父节点children中的索引
        """
        t = self.t
        full_child = parent.children[index]
        new_child = BTreeNode(full_child.leaf)
        
        # 中位数索引
        mid_index = t - 1
        
        # 将中位数关键字保存
        mid_key = full_child.keys[mid_index]
        
        # 将后半部分关键字移到新节点
        new_child.keys = full_child.keys[mid_index + 1:]
        full_child.keys = full_child.keys[:mid_index]
        
        # 如果不是叶子节点，移动子节点指针
        if not full_child.leaf:
            new_child.children = full_child.children[mid_index + 1:]
            full_child.children = full_child.children[:mid_index + 1]
        
        # 将中位数关键字上移到父节点
        parent.keys.insert(index, mid_key)
        parent.children.insert(index + 1, new_child)
    
    def delete(self, key):
        """
        从B树中删除关键字
        
        参数:
            key: 要删除的关键字
        """
        self._delete(self.root, key)
        
        # 如果根节点为空，更新根节点
        if len(self.root.keys) == 0:
            if not self.root.leaf and len(self.root.children) > 0:
                self.root = self.root.children[0]
    
    def _delete(self, node, key):
        """
        从节点中删除关键字（递归实现）
        
        参数:
            node: 当前节点
            key: 要删除的关键字
        """
        i = 0
        while i < len(node.keys) and key > node.keys[i]:
            i += 1
        
        if i < len(node.keys) and key == node.keys[i]:
            # 情况1：关键字在当前节点
            if node.leaf:
                node.keys.pop(i)
            else:
                self._delete_internal_node(node, key, i)
        elif not node.leaf:
            # 情况2：关键字在子树中
            is_in_subtree = (i == len(node.keys))
            
            # 如果子节点关键字数不足，先调整
            if len(node.children[i].keys) < self.t:
                self._fill(node, i)
            
            if is_in_subtree and i > len(node.keys):
                self._delete(node.children[i - 1], key)
            else:
                self._delete(node.children[i], key)
    
    def _delete_internal_node(self, node, key, i):
        """
        删除内部节点的关键字
        
        参数:
            node: 内部节点
            key: 要删除的关键字
            i: 关键字在节点中的索引
        """
        if node.leaf:
            node.keys.pop(i)
            return
        
        # 如果左子节点关键字数足够，用前驱替换
        if len(node.children[i].keys) >= self.t:
            predecessor = self._get_predecessor(node, i)
            node.keys[i] = predecessor
            self._delete(node.children[i], predecessor)
        # 如果右子节点关键字数足够，用后继替换
        elif len(node.children[i + 1].keys) >= self.t:
            successor = self._get_successor(node, i)
            node.keys[i] = successor
            self._delete(node.children[i + 1], successor)
        # 两个子节点关键字数都不够，合并
        else:
            self._merge(node, i)
            self._delete(node.children[i], key)
    
    def _get_predecessor(self, node, i):
        """获取前驱关键字"""
        current = node.children[i]
        while not current.leaf:
            current = current.children[-1]
        return current.keys[-1]
    
    def _get_successor(self, node, i):
        """获取后继关键字"""
        current = node.children[i + 1]
        while not current.leaf:
            current = current.children[0]
        return current.keys[0]
    
    def _fill(self, node, i):
        """
        填充子节点，使其关键字数至少为t
        
        参数:
            node: 父节点
            i: 子节点索引
        """
        # 如果前一个兄弟节点关键字数足够，从它借用
        if i != 0 and len(node.children[i - 1].keys) >= self.t:
            self._borrow_from_prev(node, i)
        # 如果后一个兄弟节点关键字数足够，从它借用
        elif i != len(node.children) - 1 and len(node.children[i + 1].keys) >= self.t:
            self._borrow_from_next(node, i)
        # 否则，与兄弟节点合并
        else:
            if i != len(node.children) - 1:
                self._merge(node, i)
            else:
                self._merge(node, i - 1)
    
    def _borrow_from_prev(self, node, child_index):
        """从前一个兄弟节点借用关键字"""
        child = node.children[child_index]
        sibling = node.children[child_index - 1]
        
        # 将父节点的关键字下移到子节点
        child.keys.insert(0, node.keys[child_index - 1])
        
        # 将兄弟节点的最后一个关键字上移到父节点
        node.keys[child_index - 1] = sibling.keys.pop()
        
        # 如果不是叶子节点，移动子节点指针
        if not child.leaf:
            child.children.insert(0, sibling.children.pop())
    
    def _borrow_from_next(self, node, child_index):
        """从后一个兄弟节点借用关键字"""
        child = node.children[child_index]
        sibling = node.children[child_index + 1]
        
        # 将父节点的关键字下移到子节点
        child.keys.append(node.keys[child_index])
        
        # 将兄弟节点的第一个关键字上移到父节点
        node.keys[child_index] = sibling.keys.pop(0)
        
        # 如果不是叶子节点，移动子节点指针
        if not child.leaf:
            child.children.append(sibling.children.pop(0))
    
    def _merge(self, node, i):
        """
        合并子节点与其兄弟节点
        
        参数:
            node: 父节点
            i: 子节点索引
        """
        child = node.children[i]
        sibling = node.children[i + 1]
        
        # 将父节点的关键字下移到左子节点
        child.keys.append(node.keys[i])
        
        # 将右兄弟节点的关键字合并到左子节点
        child.keys.extend(sibling.keys)
        
        # 如果不是叶子节点，合并子节点指针
        if not child.leaf:
            child.children.extend(sibling.children)
        
        # 从父节点中删除关键字和右子节点
        node.keys.pop(i)
        node.children.pop(i + 1)
    
    def traverse(self, node=None):
        """
        中序遍历B树
        
        参数:
            node: 从哪个节点开始遍历(默认从根节点)
        
        返回:
            遍历结果列表
        """
        if node is None:
            node = self.root
        
        result = []
        i = 0
        
        for i in range(len(node.keys)):
            # 先遍历左子树
            if not node.leaf:
                result.extend(self.traverse(node.children[i]))
            # 访问当前关键字
            result.append(node.keys[i])
        
        # 遍历最右边的子树
        if not node.leaf:
            result.extend(self.traverse(node.children[i + 1]))
        
        return result
    
    def print_tree(self, node=None, level=0):
        """
        层序打印B树
        
        参数:
            node: 从哪个节点开始打印(默认从根节点)
            level: 当前层级
        """
        if node is None:
            node = self.root
        
        print(f"{'  ' * level}Level {level}: {node.keys}")
        
        if not node.leaf:
            for child in node.children:
                self.print_tree(child, level + 1)
    
    def get_height(self, node=None):
        """
        获取B树的高度
        
        参数:
            node: 从哪个节点开始计算(默认从根节点)
        
        返回:
            树的高度
        """
        if node is None:
            node = self.root
        
        if node.leaf:
            return 1
        
        return 1 + self.get_height(node.children[0])
    
    def visualize(self):
        """打印B树的结构"""
        print("\n" + "="*60)
        print(f"B树结构 (最小度数 t={self.t})")
        print("="*60)
        self.print_tree()
        print(f"\n树的高度: {self.get_height()}")
        print(f"中序遍历: {self.traverse()}")
        print("="*60 + "\n")


# 测试代码
if __name__ == "__main__":
    print("🌲 B树实现演示\n")
    
    # 创建一个3阶B树 (t=2)
    print("创建3阶B树 (t=2, 每个节点最多3个关键字)...\n")
    btree = BTree(t=2)
    
    # 测试插入
    print("【测试1：插入操作】")
    keys_to_insert = [10, 20, 5, 6, 12, 30, 7, 17, 3, 8, 15, 18]
    print(f"依次插入: {keys_to_insert}\n")
    
    for key in keys_to_insert:
        print(f"插入 {key}...")
        btree.insert(key)
    
    btree.visualize()
    
    # 测试查找
    print("\n【测试2：查找操作】")
    search_keys = [6, 15, 100, 7]
    for key in search_keys:
        result = btree.search(key)
        if result:
            node, index = result
            print(f"✓ 找到关键字 {key} (在节点 {node.keys} 的索引 {index} 处)")
        else:
            print(f"✗ 未找到关键字 {key}")
    
    # 测试删除
    print("\n【测试3：删除操作】")
    keys_to_delete = [6, 7, 20]
    for key in keys_to_delete:
        print(f"\n删除 {key}...")
        btree.delete(key)
        btree.visualize()
    
    # 创建一个更大的B树
    print("\n" + "="*60)
    print("【测试4：大规模数据测试】")
    print("="*60)
    print("\n创建5阶B树 (t=3)...")
    large_btree = BTree(t=3)
    
    import random
    large_keys = list(range(1, 51))
    random.shuffle(large_keys)
    print(f"插入50个随机关键字: {large_keys[:10]}...")
    
    for key in large_keys:
        large_btree.insert(key)
    
    print(f"\n插入完成！")
    print(f"树的高度: {large_btree.get_height()}")
    print(f"中序遍历结果: {large_btree.traverse()[:20]}... (显示前20个)")
    
    # 性能对比
    print("\n" + "="*60)
    print("【性能分析】")
    print("="*60)
    
    import math
    
    def analyze_performance(n, t):
        """分析B树性能"""
        height = math.ceil(math.log(n + 1, t))
        print(f"\n数据量: {n:,} 条记录")
        print(f"B树阶数: {2*t} (t={t})")
        print(f"理论树高: ~{height} 层")
        print(f"最多磁盘I/O: {height} 次")
        print(f"每次I/O读取关键字数: 最多 {2*t-1} 个")
    
    analyze_performance(1000000, 2)    # 3阶B树
    analyze_performance(1000000, 50)   # 100阶B树
    analyze_performance(1000000, 500)  # 1000阶B树
    
    print("\n" + "="*60)
    print("演示完成！")
    print("="*60)


# 🌲 B树实现演示

# 创建3阶B树 (t=2, 每个节点最多3个关键字)...

# 【测试1：插入操作】
# 依次插入: [10, 20, 5, 6, 12, 30, 7, 17, 3, 8, 15, 18]

# 插入 10...
# 插入 20...
# 插入 5...
# 插入 6...
# 插入 12...
# 插入 30...
# 插入 7...
# 插入 17...
# 插入 3...
# 插入 8...
# 插入 15...
# 插入 18...

# ============================================================
# B树结构 (最小度数 t=2)
# ============================================================
# Level 0: [10]
#   Level 1: [6]
#     Level 2: [3, 5]
#     Level 2: [7, 8]
#   Level 1: [15, 20]
#     Level 2: [12]
#     Level 2: [17, 18]
#     Level 2: [30]

# 树的高度: 3
# 中序遍历: [3, 5, 6, 7, 8, 10, 12, 15, 17, 18, 20, 30]
# ============================================================


# 【测试2：查找操作】
# ✓ 找到关键字 6 (在节点 [6] 的索引 0 处)
# ✓ 找到关键字 15 (在节点 [15, 20] 的索引 0 处)
# ✗ 未找到关键字 100
# ✓ 找到关键字 7 (在节点 [7, 8] 的索引 0 处)

# 【测试3：删除操作】

# 删除 6...

# ============================================================
# B树结构 (最小度数 t=2)
# ============================================================
# Level 0: [15]
#   Level 1: [5, 10]
#     Level 2: [3]
#     Level 2: [7, 8]
#     Level 2: [12]
#   Level 1: [20]
#     Level 2: [17, 18]
#     Level 2: [30]

# 树的高度: 3
# 中序遍历: [3, 5, 7, 8, 10, 12, 15, 17, 18, 20, 30]
# ============================================================


# 删除 7...

# ============================================================
# B树结构 (最小度数 t=2)
# ============================================================
# Level 0: [15]
#   Level 1: [5, 10]
#     Level 2: [3]
#     Level 2: [8]
#     Level 2: [12]
#   Level 1: [20]
#     Level 2: [17, 18]
#     Level 2: [30]

# 树的高度: 3
# 中序遍历: [3, 5, 8, 10, 12, 15, 17, 18, 20, 30]
# ============================================================


# 删除 20...

# ============================================================
# B树结构 (最小度数 t=2)
# ============================================================
# Level 0: [10]
#   Level 1: [5]
#     Level 2: [3]
#     Level 2: [8]
#   Level 1: [15, 18]
#     Level 2: [12]
#     Level 2: [17]
#     Level 2: [30]

# 树的高度: 3
# 中序遍历: [3, 5, 8, 10, 12, 15, 17, 18, 30]
# ============================================================


# ============================================================
# 【测试4：大规模数据测试】
# ============================================================

# 创建5阶B树 (t=3)...
# 插入50个随机关键字: [13, 5, 39, 22, 41, 20, 25, 44, 32, 15]...

# 插入完成！
# 树的高度: 3
# 中序遍历结果: [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20]... (显示前20个)

# ============================================================
# 【性能分析】
# ============================================================

# 数据量: 1,000,000 条记录
# B树阶数: 4 (t=2)
# 理论树高: ~20 层
# 最多磁盘I/O: 20 次
# 每次I/O读取关键字数: 最多 3 个

# 数据量: 1,000,000 条记录
# B树阶数: 100 (t=50)
# 理论树高: ~4 层
# 最多磁盘I/O: 4 次
# 每次I/O读取关键字数: 最多 99 个

# 数据量: 1,000,000 条记录
# B树阶数: 1000 (t=500)
# 理论树高: ~3 层
# 最多磁盘I/O: 3 次
# 每次I/O读取关键字数: 最多 999 个

# ============================================================
# 演示完成！
# ============================================================

5、可视化演示

https://code.juejin.cn/pen/7563648208417603635?embed=true

6、时间复杂度分析

B树的性能分析与传统的内存数据结构不同，我们更关心的是磁盘I/O次数 ，因为这才是主要的时间开销。设树中总共有 n 个关键字，最小度数为 t。

6.1、 B树的高度

B树所有性能优势的根源在于其极低的高度 h。由于除了根节点，每个节点至少有 t 个子节点，因此树的"分支因子"非常大。一棵包含 n 个关键字、最小度数为 t (t>=2) 的B树，其高度 h 的上限为：

h ≤ logₜ((n+1)/2)

这意味着树的高度与总关键字数 n 是以 t 为底的对数关系。

这里的关键是底数 t。对于磁盘操作，t 的值通常很大（例如，如果一个磁盘块是4KB，每个关键字和指针占8字节，那么 t 可以轻松达到 4096 / (8*2) = 256）。

让我们用一个具体的例子来感受一下：假设我们有一百万 条记录 (n = 1,000,000)。

如果用二叉搜索树，高度大约是 log₂(1,000,000) ≈ 20。最坏情况下需要20次磁盘I/O。
如果用B树，且最小度数 t = 100，高度大约是 log₁₀₀(1,000,000 / 2) ≈ log₁₀₀(500,000) = 2.85。这意味着最多只需要 3 次磁盘I/O！

从20次I/O骤降到3次，性能提升是巨大的。这就是B树"矮胖"身材的威力所在。

6.2、操作复杂度

所有核心操作的复杂度都与树的高度 h 成正比。

操作	磁盘I/O复杂度	CPU计算复杂度	说明
查找	`O(h) = O(logₜ n)`	`O(h * log t) = O(logₜ n * log t)`	树的高度决定I/O次数
插入	`O(h) = O(logₜ n)`	`O(h * t) = O(t * logₜ n)`	需要查找位置+可能的分裂
删除	`O(h) = O(logₜ n)`	`O(h * t) = O(t * logₜ n)`	需要查找+可能的合并

磁盘I/O ：每次操作都需要从根节点遍历到叶子节点，涉及的磁盘读写次数与树高 h 成正比，所以都是 O(logₜ n)。这是我们最关心的指标。
CPU计算 ：
- 查找：在每个节点内部进行二分查找，耗时 O(log t)。总耗时为 h * O(log t)。
- 插入/删除 ：在最坏情况下，可能需要沿着路径一直向上进行分裂或合并。每次分裂/合并操作需要移动关键字和指针，耗时与节点大小成正比，即 O(t)。总耗时为 h * O(t)。

总而言之，由于磁盘I/O的时间远超CPU计算时间，我们可以认为B树所有核心操作的时间复杂度就是其磁盘I/O的复杂度：O(logₜ n)。

7、B树的应用

B树及其变体（特别是B+树）的设计初衷就是为了优化磁盘等慢速、块存储设备的访问效率，因此它们最经典的应用场景是数据库索引 和文件系统。

8、B树的变种

B树有一个非常重要的变体------B+树，它在数据库索引（如MySQL的InnoDB引擎）中的应用更为广泛。

特性	B树 (B-Tree)	B+树 (B+ Tree)
数据存储位置	所有节点（内部节点和叶子节点）都存储关键字和数据指针。	只有叶子节点存储关键字和数据指针。内部节点只存储关键字，作为索引。
冗余关键字	内部节点的关键字是唯一的。	内部节点的关键字会作为"路标"在叶子节点中重复出现。
叶子节点连接	叶子节点之间没有链接。	所有叶子节点通过指针串联成一个有序的双向链表。
查询效率	单点查询可能更快，因为数据可能在内部节点找到，无需到达叶子。	所有查询都必须到达叶子节点，路径长度稳定。范围查询和遍历极其高效，只需扫描叶子链表。
空间利用率	较低，因为内部节点要存数据。	更高，内部节点不存数据，可以容纳更多关键字，使得树更"矮胖"。

B*树是B+树的另一个变体，它在B+树的基础上，要求非根节点的关键字填充率更高（从1/2提升到2/3），并且在节点满时，会尝试将关键字分配给兄弟节点，而不是立即分裂，从而进一步提高了空间利用率。

后面会有文章单独讲解这两种结构，这里先了解下就行

9、总结

B树不是为内存而生的数据结构，它的所有设计精髓都围绕着一个核心目标：最大限度地减少磁盘I/O。

通过多路（而非二路）分支，构建矮胖的树形结构，从根本上减少了从根到叶的访问层数。
节点大小设计为与磁盘块大小相匹配，实现了一次IO，最大化信息加载、。
通过分裂和合并/旋转机制，实现了动态的自我平衡，保证了在频繁增删后依然能维持低高度和高效率。