队列原理与实现全解析

文章目录

[1. 队列的基本概念](#1. 队列的基本概念)
- [1.1 概念](#1.1 概念)
- [1.2 队列相关概念](#1.2 队列相关概念)
- [1.3 队列的基本操作](#1.3 队列的基本操作)
[2. 队列的顺序存储结构](#2. 队列的顺序存储结构)
- [2.1 顺序队列](#2.1 顺序队列)
- [2.2 循环队列](#2.2 循环队列)
- [2.3 顺序队列的基本操作代码](#2.3 顺序队列的基本操作代码)
- - [2.3.1 初始化](#2.3.1 初始化)
  - [2.3.2 队列空](#2.3.2 队列空)
  - [2.3.3 队列满](#2.3.3 队列满)
  - [2.3.4 入队](#2.3.4 入队)
  - [2.3.5 出队](#2.3.5 出队)
  - [2.3.6 读队头](#2.3.6 读队头)
  - [2.3.7 获取队列元素个数](#2.3.7 获取队列元素个数)
[3. 队列的链式存储结构](#3. 队列的链式存储结构)
- [3.1 链式队列结构](#3.1 链式队列结构)
- [3.2 链式队列基本操作代码实现](#3.2 链式队列基本操作代码实现)
- - [3.2.1 初始化](#3.2.1 初始化)
  - [3.2.2 队列空](#3.2.2 队列空)
  - [3.2.3 入队](#3.2.3 入队)
  - [3.2.4 出队](#3.2.4 出队)
  - [3.2.5 读队头](#3.2.5 读队头)
  - [3.2.6 销毁队列](#3.2.6 销毁队列)

1. 队列的基本概念

1.1 概念

队列是一种特殊的线性表，只允许在一端进行插入数据操作，在另一端进行删除数据操作的一种数据结构。队列具有先进先出(First In First Out，简称FIFO) 的原则。

队列（Queue）是一种特殊的线性数据结构，其操作遵循先进先出（First In, First Out, FIFO）的原则。即元素的插入只能在队列的一端进行，而删除操作则在另一端执行。这种单向进出的特性使得最早进入队列的元素能够最先被移除，广泛应用于任务调度、缓冲处理、广度优先搜索等场景。

1.2 队列相关概念

队尾：进行插入操作的一端称为队尾，队尾指向的是最后一个元素

队头：进行删除操作的一端称为队头，队头指向的是第一个元素

入队：将一个元素添加到队尾的操作称为入队

出队：从队头取出一个元素的操作称为出队

队尾（Rear）：进行插入操作的一端，新元素从队尾加入。队尾指针通常指向当前最后一个有效元素的位置。
队头（Front）：进行删除操作的一端，元素从此处移出。队头指针指向当前最前端的元素。
入队（Enqueue）：将一个新元素添加到队尾的操作。
出队（Dequeue）：从队头移除一个元素的操作。

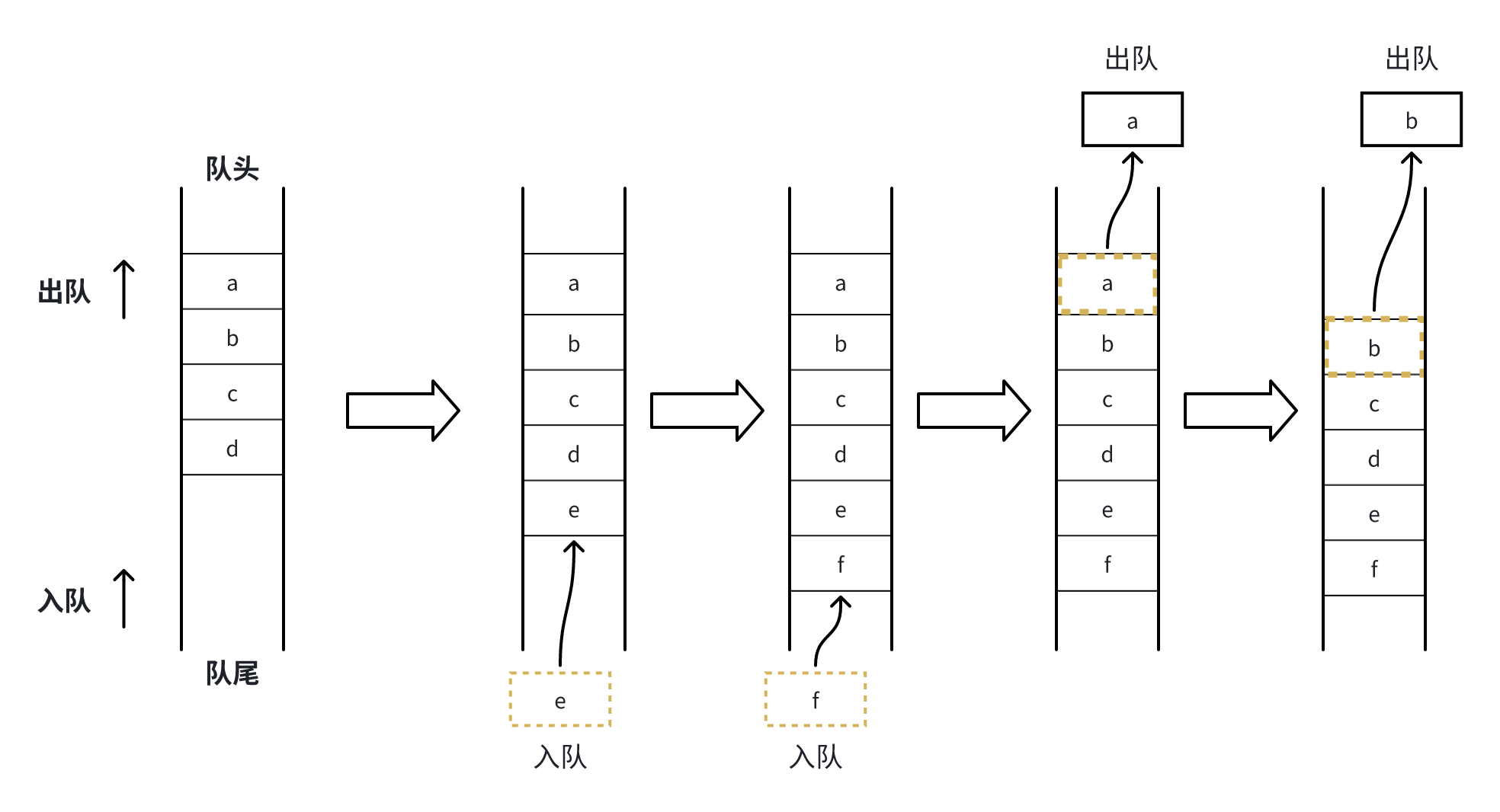
1.3 队列的基本操作

队列的核心操作通常包括：

入队
出队
获取队头元素
判断队列是否为空

队列的物理实现主要有两种方式：基于数组（顺序存储）和基于链表（链式存储）。其中，基于数组的实现又可进一步分为顺序队列和循环队列。

2. 队列的顺序存储结构

使用数组实现队列称为顺序存储结构。为高效管理队列状态，需定义两个指针：

front：指向队头元素的位置

rear：指向下一个可插入位置（即队尾后一位）

本文统一采用 front 和 rear 表示队头与队尾指针，特殊说明除外。

2.1 顺序队列

顺序队列使用一组地址连续的存储单元（数组）依次存放从队头到队尾的元素。同时，设置队头指针 front和队尾指针 rear。其结构定义示例如下：

c 复制代码

#define MAX_SIZE 100 //设置队列最大存储元素个数
typedef struct
{
	//定义元素结构
} ElementType
// 定义队列结构体
typedef struct
{
    ElementType data[MAX_SIZE];
    int front;
    int rear;
} ArrayQueue;

请注意，我们在此使用"元素"而非"数据"来指代队列的组成单元，是因为队列中的单元可以是基本数据类型、数组、结构体等任何有效数据类型。

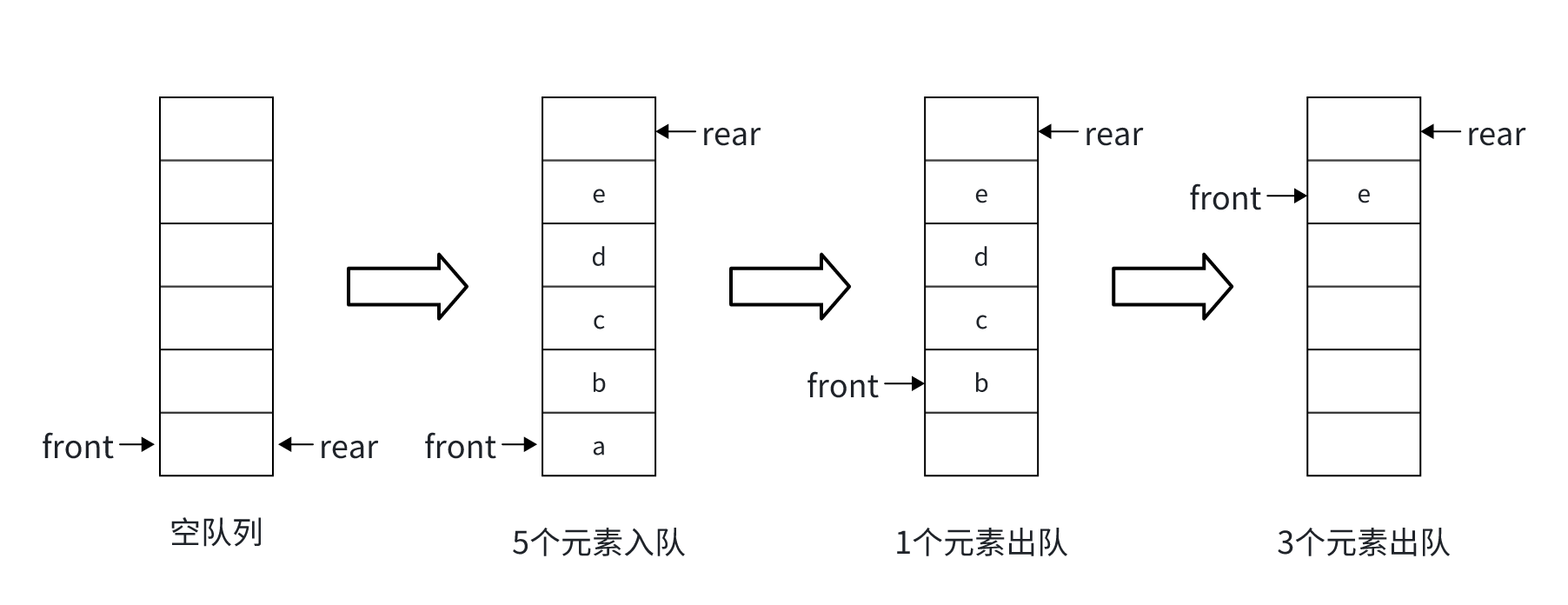
如上图所示，在顺序队列中：

入队时，rear指针向后移动，front指针不变。
出队时，front指针向后移动，rear指针不变。
基础的入队和出队操作代码如下：

c 复制代码

// 入队
int enqueueArray(ArrayQueue *q, ElementType e)
{
    if (q->rear >= MAX_SIZE) {
        printf("队列已满\n");
        return -1;  // 失败
    }
    q->data[q->rear++] = e;
    return 0;  // 成功
}
// 出队
int dequeueArray(ArrayQueue *q, ElementType *e) {
    if (q->front == q->rear) {
        printf("队列为空\n");
        return -1;
    }
    *e = q->data[q->front++];
    return 0;
}

上述代码逻辑简单直接。但考虑一种情况：如果队列在执行若干次出队操作后，front指针前移，此时即使数组尾部仍有空间，新元素入队时也可能因 rear指针到达数组末尾而被误判为队列已满。

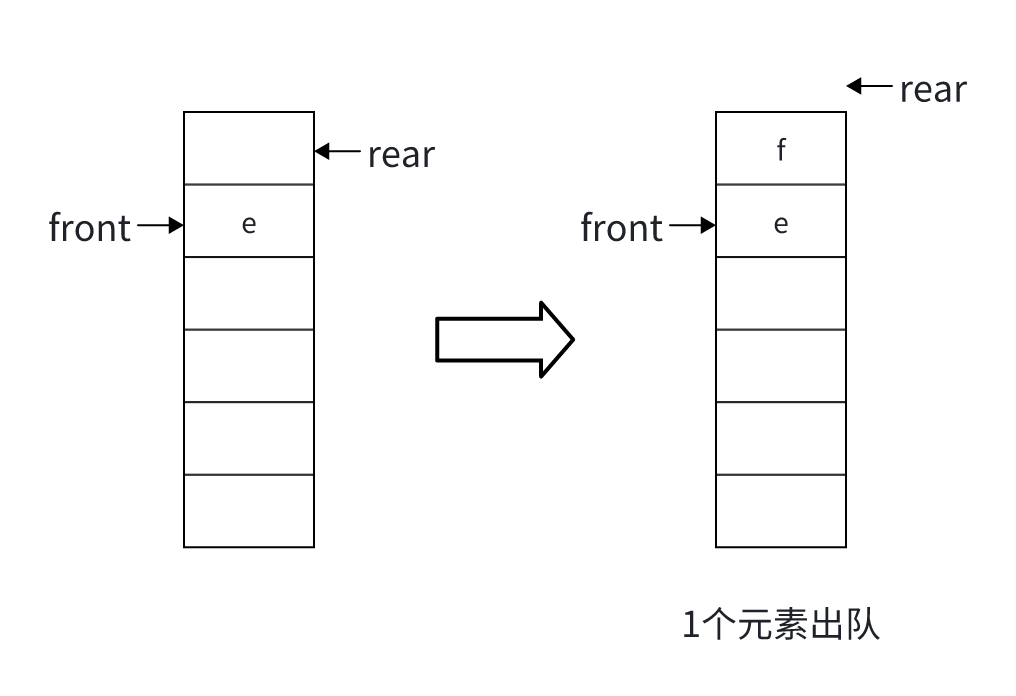
此时，q->rear >= MAX_SIZE，满足队列已满 的判断条件，但是队列还有4个元素空间可存储，这种情况被称为："假溢出"。

到这里，你可能会有这样的疑问：出队时为什么队头要往后移动而不是一直指向数组下标为0的位置？

若强制 front 始终为 0，则每次出队后需将后续所有元素前移一位，造成频繁的数据迁移，时间复杂度为 O(n)，严重影响性能。因此，采用移动 front 指针的方式避免实时迁移，仅在必要时整体前移数据。

对于顺序队列，我们可以采用如下方法：

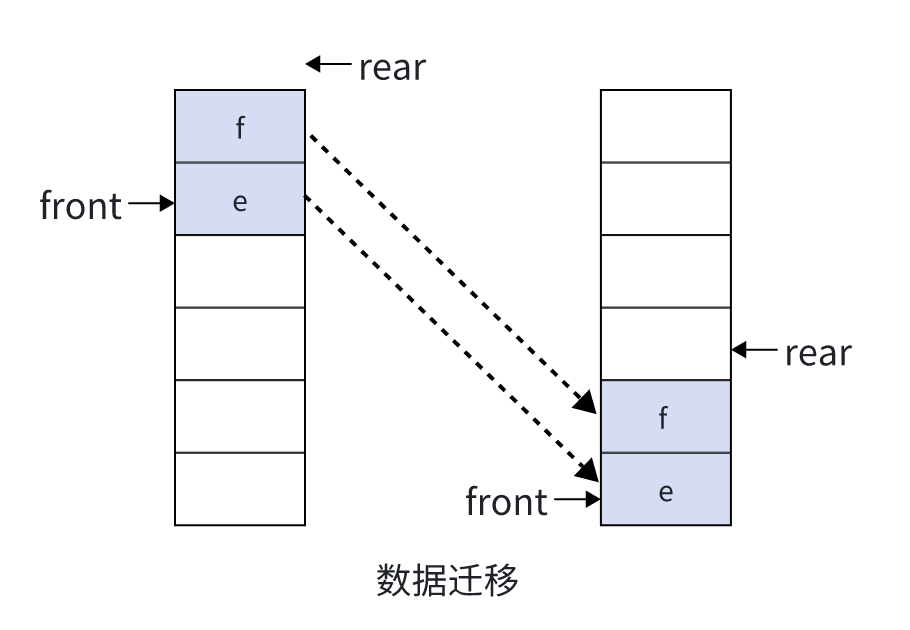
如果我们出队时，队头往后移动一位，这样我们就避免每次出队都进行数据迁移，我们只需要在只有在rear等于数组大小且front不等于0时，进行一次数据迁移，将已经出队留下的空间继续供入队时使用。

尽管该方法减少了迁移频率，但仍无法彻底消除，性能仍受限。为此，引入更优的解决方案------循环队列

2.2 循环队列

循环队列是对顺序队列的改进，通过将数组逻辑上首尾相连，形成一个环形结构，从而解决"假溢出"问题。

当 rear 到达数组末尾时，自动回到下标 0，实现空间的循环利用。同理，front 也可循环移动。

先来看看循环队列的入队、出队操作：

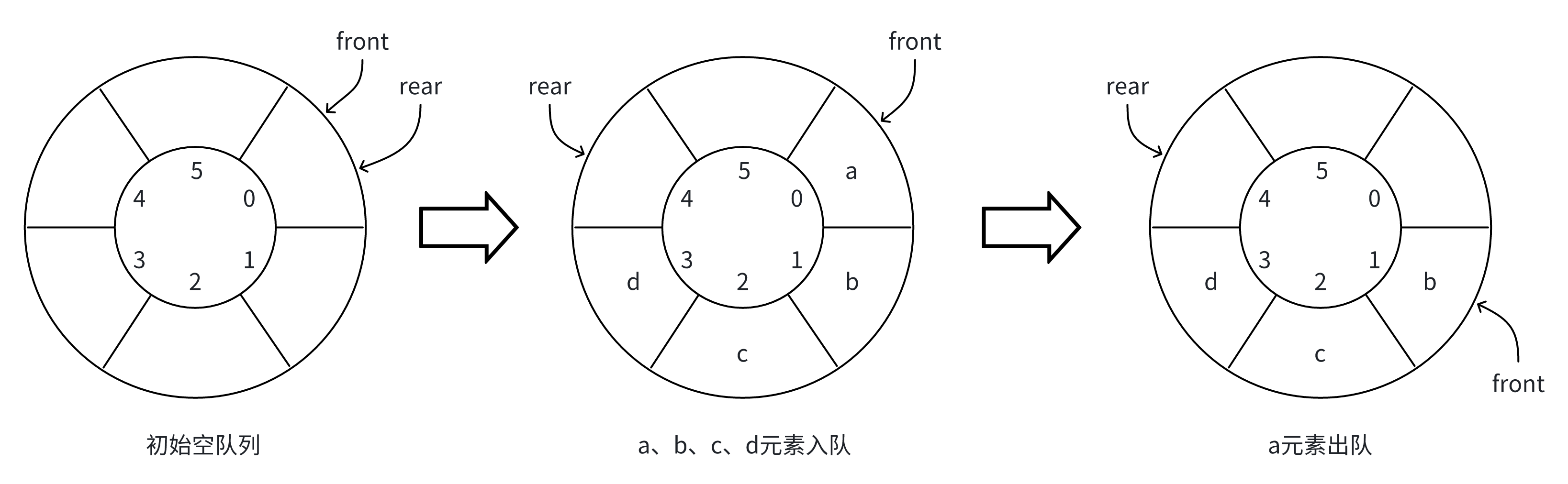
如果使用循环队列的方式，当队列为空以及队列满的时候，front和rear指针都是出于重叠的状态，即front==rear，这就会出现歧义了，这会让我们分辨不清当front和rear重叠的时候，队列是空的还是队满状态。

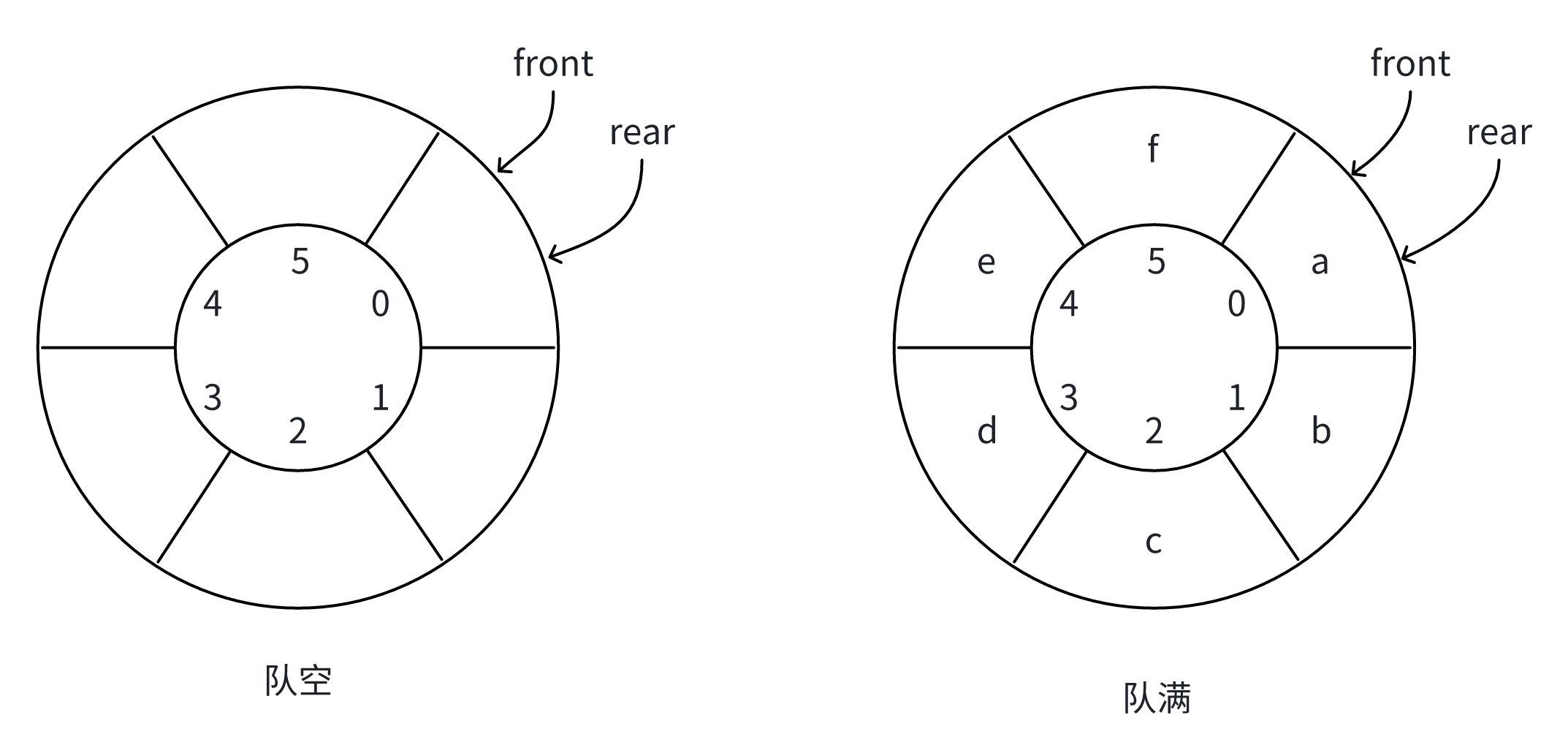
循环队列避免了"假溢出"的问题，又如何解决循环队列"队空"和"队满"判断的问题？

有三种方式区分"队空"和"队满"：

结构体中增加一个计数器，用以记录队列中元素数量

优点：逻辑清晰，判断高效
缺点：多占用一个整型空间

c 复制代码

// 定义队列结构体
typedef struct
{
    ElementType data[MAX_SIZE];
    int front;
    int rear;
    int cnt; // 元素个数
} CircularQueue;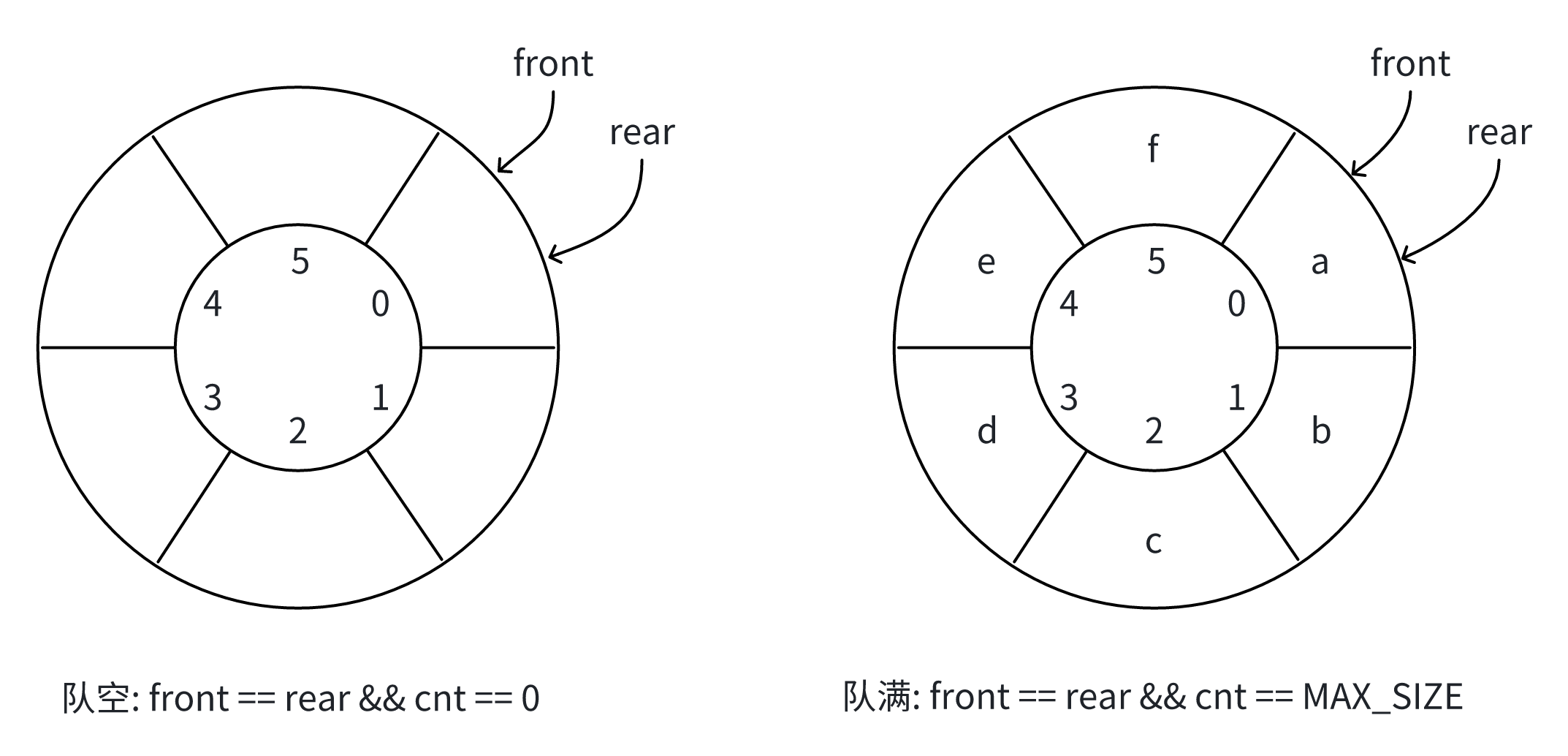

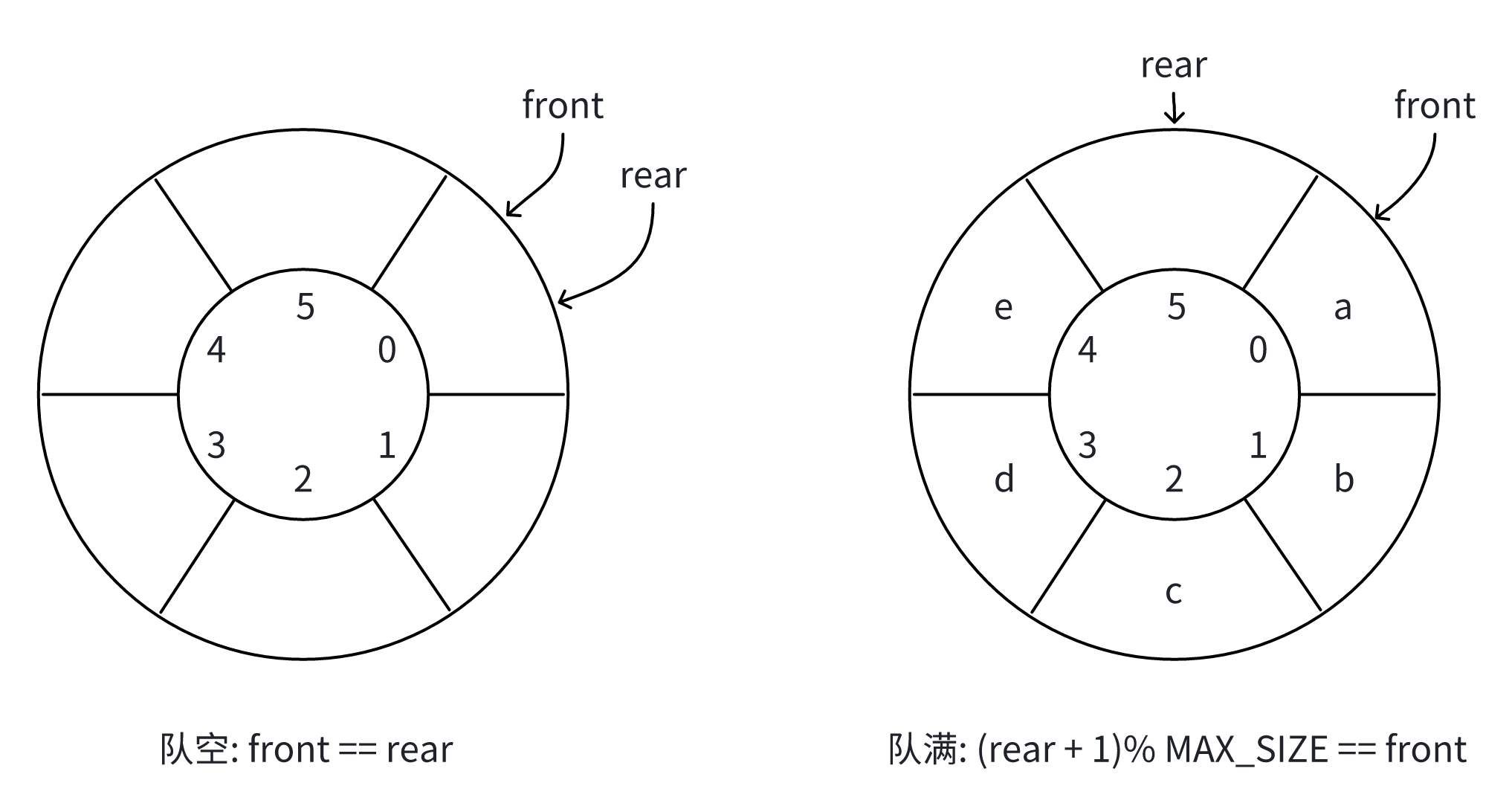
牺牲一个存储单元（常用方法）
牺牲一个队列单元来区分队空和队满，入队时少用一个队列单元，这是种较为普遍的做法，约定以"队头指针在队尾指针的下一位置作为队满的标志"

约定：队列最多存放 MAX_SIZE-1 个元素，保留一个空位用于区分空满状态。

队空条件：front == rear

队满条件：(rear + 1) % MAX_SIZE == front

优点：无需额外变量，实现简洁，广泛用于标准库和竞赛编程
缺点：牺牲一个存储单元

设置状态标志 flag
引入一个标志位，标识上一次操作是入队还是出队，辅助判断当前状态。

优点：节省空间，适合内存敏感场景
缺点：逻辑较复杂，易出错，维护成本高

c 复制代码

// 定义队列结构体
typedef struct
{
    ElementType data[MAX_SIZE];
    int front;
    int rear;
    int flag;
} CircularQueue;

这种方式和第1种类似，只是第1种方法是定量判断，flag判断是定性判断，逻辑上不如记录数量的方法简单，且容易理解。

2.3 顺序队列的基本操作代码

以循环队列为例（牺牲一个存储单元的方案）

2.3.1 初始化

c 复制代码

void initQueue(CircularQueue *q)
{
    q->front = 0;
    q->rear = 0;
}

2.3.2 队列空

c 复制代码

bool isEmpty(CircularQueue *q)
{
    return q->front == q->rear;
}

2.3.3 队列满

c 复制代码

bool isFull(CircularQueue *q)
{
    return (q->rear + 1) % MAX_SIZE == q->front;
}

2.3.4 入队

c 复制代码

bool enqueue(CircularQueue *q, int value)
{
    if (isFull(q)) {
        printf("队列已满，无法入队\n");
        return false;
    }
    q->data[q->rear] = value;
    q->rear = (q->rear + 1) % MAX_SIZE;
    return true;
}

2.3.5 出队

c 复制代码

bool dequeue(CircularQueue *q, int *value)
{
    if (isEmpty(q))
    {
        printf("队列为空，无法出队\n");
        return false;
    }
    *value = q->data[q->front];
    q->front = (q->front + 1) % MAX_SIZE;
    return true;
}

2.3.6 读队头

c 复制代码

bool getFront(CircularQueue *q, int *value)
{
    if (isEmpty(q))
    {
        printf("队列为空\n");
        return false;
    }
    *value = q->data[q->front];
    return true;
}

2.3.7 获取队列元素个数

c 复制代码

int getSize(CircularQueue *q)
{
    return (q->rear - q->front + MAX_SIZE) % MAX_SIZE;
}

3. 队列的链式存储结构

3.1 链式队列结构

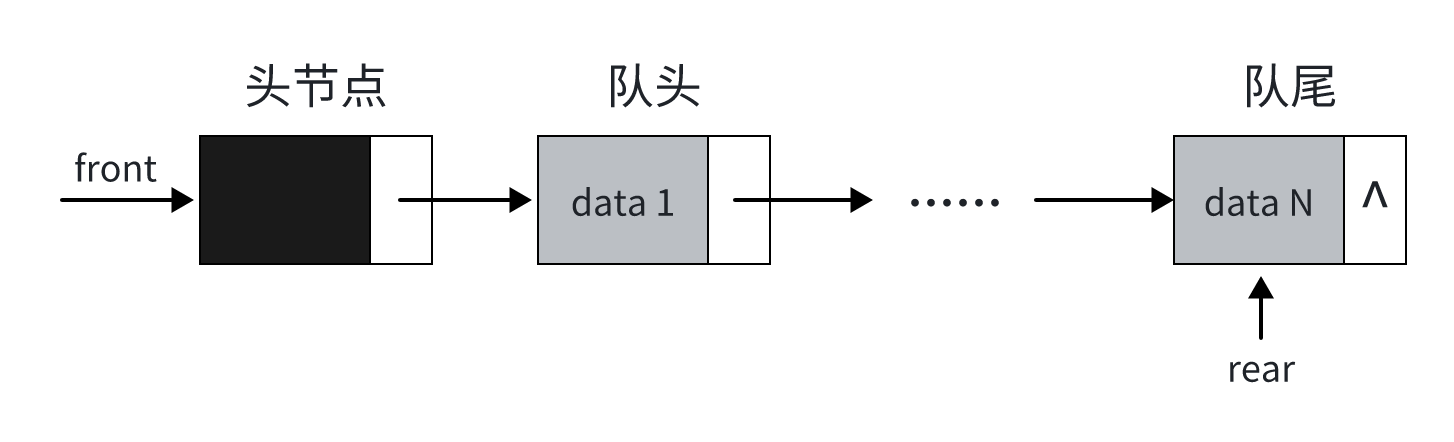
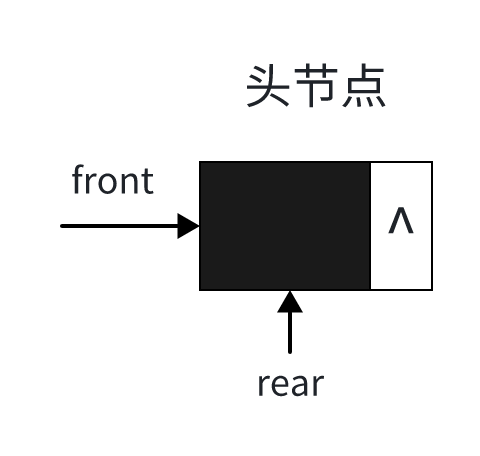
链式队列基于单链表实现，由一系列节点构成，每个节点包含数据域和指向下一节点的指针。队列维护两个外部指针：

队头指针（front）：指向链表的第一个节点
队尾指针（rear）：指向链表的最后一个节点

操作流程

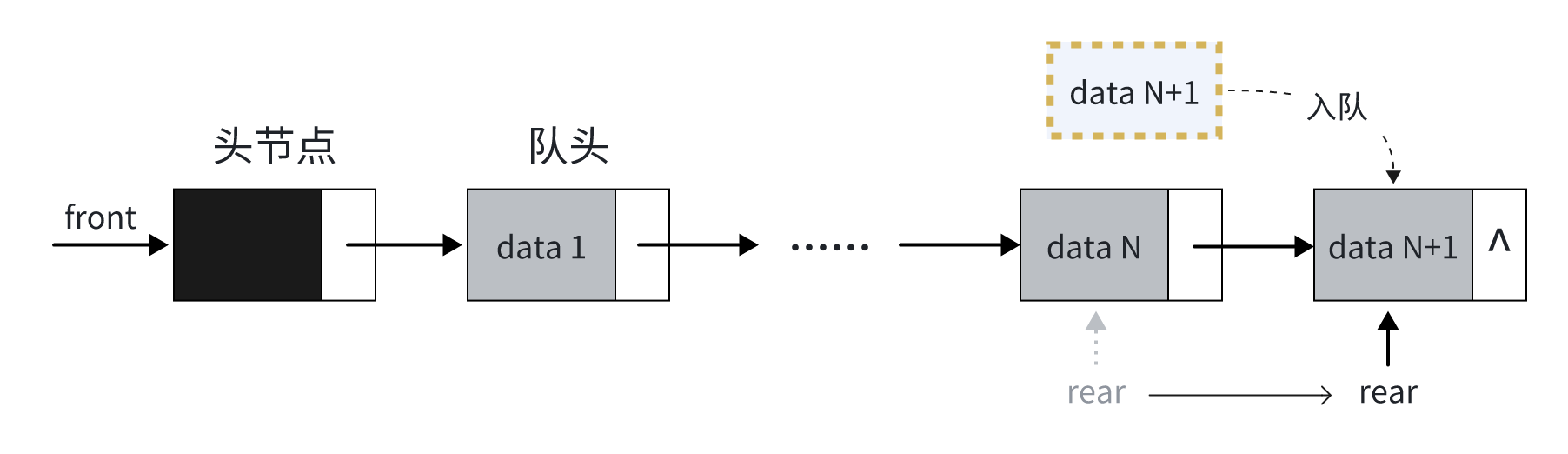
入队：在 rear 后创建新节点，并更新 rear 指针

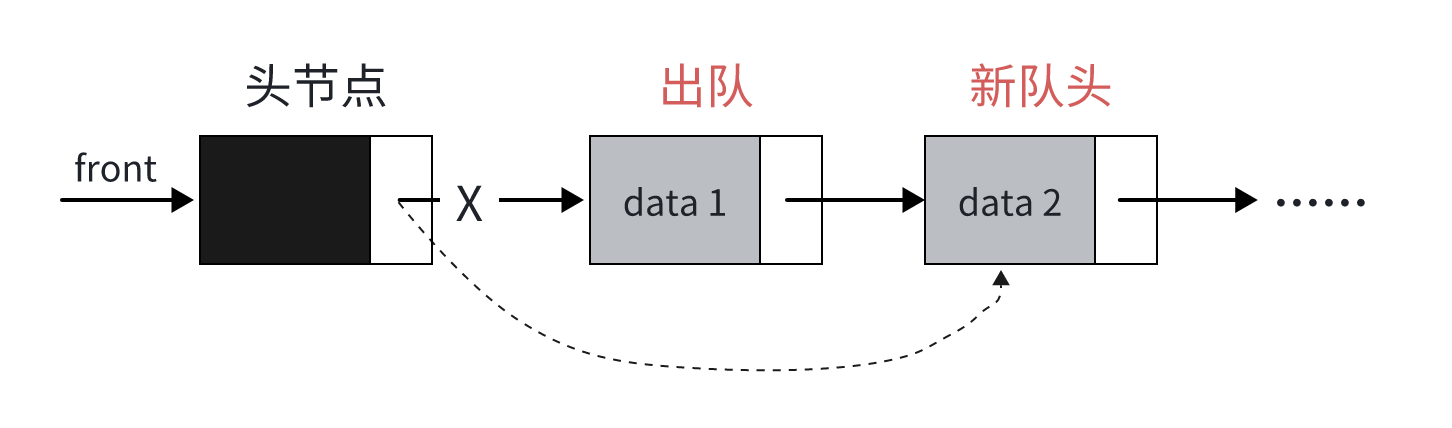
出队：删除 front 所指节点，释放内存，并将 front 移至下一个节点

优点

动态分配内存，无需预设容量
无"假溢出"问题，空间利用率高
插入删除效率高（O(1)）
缺点
每个节点需额外存储指针，空间开销大
内存分配/释放带来一定时间开销
存在内存碎片风险（频繁申请释放）

链式队列

入队

出队

头节点

3.2 链式队列基本操作代码实现

3.2.1 初始化

节点与队列结构定义

c 复制代码

// 链式队列节点定义
typedef struct QueueNode {
    int data;
    struct QueueNode *next;
} QueueNode;

// 链式队列结构定义
typedef struct {
    QueueNode *front;
    QueueNode *rear;
} LinkedQueue;
// 初始化队列
void initLinkedQueue(LinkedQueue *q) {
    q->front = NULL;
    q->rear = NULL;
}

3.2.2 队列空

c 复制代码

// 判断队列是否为空
bool isLinkedQueueEmpty(LinkedQueue *q) {
    return q->front == NULL;
}

3.2.3 入队

c 复制代码

bool enqueueLinked(LinkedQueue *q, int value) {
    QueueNode *newNode = (QueueNode*)malloc(sizeof(QueueNode));
    if (newNode == NULL) {
        printf("内存分配失败\n");
        return false;
    }
    newNode->data = value;
    newNode->next = NULL;
    if (isLinkedQueueEmpty(q)) {
        // 队列为空时，front和rear都指向新节点
        q->front = newNode;
        q->rear = newNode;
    } else {
        // 队列不为空时，将新节点添加到rear后面
        q->rear->next = newNode;
        q->rear = newNode;
    }
    return true;
}

3.2.4 出队

c 复制代码

// 出队操作
bool dequeueLinked(LinkedQueue *q, int *value) {
    if (isLinkedQueueEmpty(q)) {
        printf("队列为空，无法出队\n");
        return false;
    }
    QueueNode *temp = q->front;
    *value = temp->data;
    q->front = q->front->next;
    // 如果出队后队列为空，需要更新rear指针
    if (q->front == NULL) {
        q->rear = NULL;
    }
    free(temp);
    return true;
}

3.2.5 读队头

c 复制代码

bool getFrontLinked(LinkedQueue *q, int *value) {
    if (isLinkedQueueEmpty(q)) {
        printf("队列为空\n");
        return false;
    }
    
    *value = q->front->data;
    return true;
}

3.2.6 销毁队列

c 复制代码

// 销毁队列
void destroyLinkedQueue(LinkedQueue *q) {
    int value;
    while (!isLinkedQueueEmpty(q)) {
        dequeueLinked(q, &value);
    }
}