点云数据分割算法之-聚合层次聚类（AHC）平面识别

算法原文：Fast Plane Extraction in Organized Point Clouds Using Agglomerative Hierarchical Clustering

1. 简介（Introduction）

随着低成本深度相机（如 Kinect）和 3D 传感器的普及，获取有序点云（organized point cloud）变得容易。这类点云在机器人和计算机视觉中广泛应用，但原始点云通常存在噪声、冗余，并缺乏语义信息。为了对 3D 场景进行紧凑、语义化建模，原始形状拟合（primitive fitting）成为一种重要方法，其中平面 是最关键的原始形状，因为人工环境（建筑、家具等）大多由平面构成。

本文提出了一种针对有序点云的高效平面提取算法，基于聚合层次聚类（Agglomerative Hierarchical Clustering, AHC），实现了实时性和高精度。

---

2. 算法背景（Related Work）

2.1 平面提取方法

1. RANSAC方法

   • 利用随机采样一致性（RANSAC）迭代寻找平面模型并剔除内点。
   • 缺点：随机采样选择和平面拟合计算开销大，速度慢。
   • 改进：局部RANSAC、Hough变换预分割等。

2. 区域生长方法（Region Growing）

   • 根据点到平面的距离或 MSE 阈值，将邻近点扩展到平面。
   • 缺点：需要每个点的法线估计，计算量大。

3. 图结构方法（Graph-based）

   • 将点云构建成图，通过节点和边表示点的聚类关系。

   • 本文方法与前人区别：

     • 不使用 RGB 信息
     • 不需要每点法线估计
     • 使用动态边权，自动选择合并顺序

2.2 平面在应用中的重要性

• 室内/室外三维重建与可视化
• 桌面物体操作（通过主要平面分割物体）
• SLAM 与定位（平面作为比点更稳定的地标）

---

3. 文章贡献（Contributions / 创新点）

1. 高效的平面提取算法：

   • 基于聚合层次聚类的算法适用于有序点云
   • 不依赖每点法线估计，速度更快

2. 复杂度分析：

   • 聚类复杂度为 对数线性（log-linear）
   • 能够实现实时性

3. 实验验证：

   • 对比最先进算法
   • 对 640×480 点云，运行频率超过 35 Hz
   • 精度与最先进方法可比

---

4. 需解决的关键问题

1. 噪声与冗余数据：点云中噪声、缺失点或深度突变可能影响平面拟合。
2. 平面边界精度：粗分割可能导致锯齿状边界（sawtooth）、过度分割或未分配数据点。
3. 合并策略效率：如何在保证精度的前提下快速完成节点合并。
4. 非重叠节点初始化：需要在图像空间均匀划分初始节点，避免重复点，提高速度。

---

5. 论文提出的算法流程（Algorithm Overview）

算法整体流程概览

1. 输入

   • 有序点云 F （organized point cloud，M×NM \times NM×N 点），如 Kinect 或深度相机获取的深度图。

2. 输出

   • 粗平面分割 B 和精细平面分割 C
   • 对应的平面方程集 Π （粗）和 Π₀（精细）

3. 三大步骤

   1. 图初始化 (Graph Initialization)
   2. 粗平面提取 (Agglomerative Hierarchical Clustering, AHC)
   3. 精细化分割 (Segmentation Refinement)

---

步骤 1：图初始化 (Graph Initialization)

目标：将有序点云划分为非重叠的初始节点，并构建图结构，节点表示点集，边表示邻居关系。

1. 将点云 F 按 H×WH \times WH×W 的大小均匀划分为初始节点 vi,jv_{i,j}vi,j。

2. 剔除不良节点（REJECTNODE）：

   • 节点包含缺失数据
   • 节点包含深度不连续点
   • 节点平面拟合 MSE 过大

3. 初始化图边（REJECTEDGE）：

   • 根据节点法向量判断边是否保留，避免平面方向差异太大

4. 得到图 G = (V, E)，用于后续 AHC 合并

---

步骤 2：粗平面提取 (AHC)

目标：通过自底向上的层次聚类，将属于同一平面的节点合并。

1. 为所有节点建立 最小 MSE 堆，快速找到当前最优合并节点。

2. 循环执行：

   1. 取 MSE 最小的节点 vvv

   2. 对每个邻居 u∈N(v)u \in N(v)u∈N(v)，尝试合并：

      • 计算合并后节点 umerge=v∪uu_\text{merge} = v \cup uumerge=v∪u 的平面拟合 MSE
      • 选择合并后 MSE 最小的邻居 ubestu_\text{best}ubest

   3. 判断合并结果：

      • 如果 MSE(umerge)>TMSEMSE(u_\text{merge}) > T_\text{MSE}MSE(umerge)>TMSE → 合并失败，将节点 vvv 提取为一个粗平面
      • 否则 → 合并成功，更新图结构和堆

3. 输出粗平面集合 B 和对应平面方程 Π

关键优化：

• 使用 最小堆快速找到最优节点 → O(n log n)
• 节点合并时利用积分图或统计量 → 平面拟合 MSE 计算为常数时间
• 图为平面图，平均节点度 < 6 → 合并尝试次数有限

---

步骤 3：精细化分割 (Segmentation Refinement)

目标：修正粗分割中的边界错误、过分割或缺失点，提高平面精度。

1. 腐蚀边界 (Erosion)：

   • 移除每个粗分割段 B 的边界节点，去掉锯齿状伪影。

2. 区域生长 (Region Growing)：

   • 从腐蚀后的边界节点出发，按像素级邻居分配未使用的点到最近的平面段
   • 更新小图 G₀ 中的节点和边

3. 最终合并 (AHC)：

   • 在小图 G₀ 上再次执行 AHC 修正过分割问题

4. 输出精细分割 C 和精细平面方程 Π₀

---

6. 核心方法细节（Core Method Details）

6.1 算法概述

图 2 展示了我们算法如何处理每一帧组织化点云。我们将 组织化点云 定义为一组二维索引的三维点

F=pi,j=(xi,j,yi,j,zi,j)T,i=1,...,M, j=1,...,N, F = { p_{i,j} = (x_{i,j}, y_{i,j}, z_{i,j})^T }, \quad i=1,\dots,M,\ j=1,\dots,N, F=pi,j=(xi,j,yi,j,zi,j)T,i=1,...,M, j=1,...,N,

其中二维索引 (i,j)(i,j)(i,j) 和 (i±1,j±1)(i \pm 1, j \pm 1)(i±1,j±1) 反映了点 pi,jp_{i,j}pi,j 与 pi±1,j±1p_{i\pm1,j\pm1}pi±1,j±1 在同一表面上的三维邻近关系（我们将该索引空间称为 图像空间 ）。通常，它可以从深度图中获得，该深度图由 Kinect 传感器、飞行时间相机、结构光扫描系统，甚至通过旋转激光测距仪的扫描平面生成。

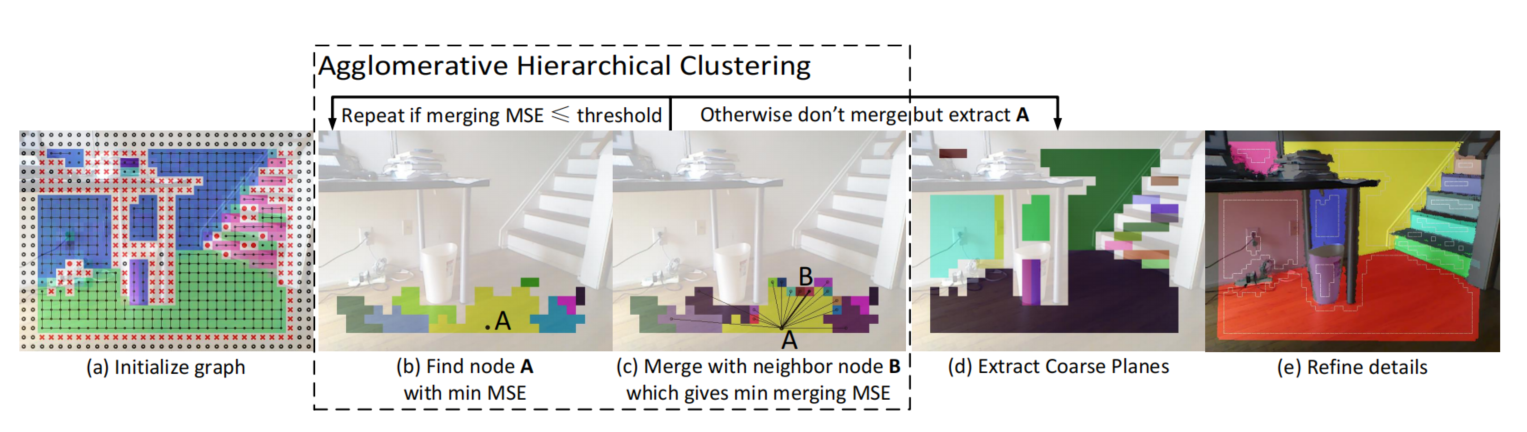
图 2. 算法概览。每一帧有序点云从左到右进行处理。(a) 显示图的初始化，每个节点根据其法向量着色；黑点和黑线表示图的节点和边；红色 "x"、黑色 "o"、红点分别表示因深度不连续、数据缺失和平面拟合均方误差过大而被拒绝的节点。(b) 和 © 显示 AHC 的两个核心操作。(b) 和 © 中随机颜色的区域表示至少被合并过一次的图节点。© 中黑色线条表示从节点 A 出发的所有边，其中粗线表示当节点 A 与其邻居合并时，产生最小平面拟合均方误差的边对应的节点 B。(d) 中彩色区域表示提取出的粗平面，如果应用需要，则在 (e) 中进行最终精细化。

---

A. 以线段提取为类比

在进入我们算法细节之前，我们简要讨论一个称为 线回归 (line regression) 的线段提取算法，如文献 [21] 所总结，并在 April Robotics Toolkit [22] 中实现。该方法广泛用于从激光测距仪获取的二维点序列中提取线特征，并启发我们将其推广到三维点云中的快速平面提取。

如图 3 所示，序列中每 W 个连续点 （此图中 W=3W=3W=3）被分组为节点，形成一个 双向链表。然后对该链表执行 AHC（Agglomerative Hierarchical Clustering，自底向上的层次聚类）：

1. 找到具有最小线拟合均方误差 (MSE) 的节点 ggg；
2. 将节点 ggg 与其左邻居或右邻居合并，使合并后的 MSE 最小。
   
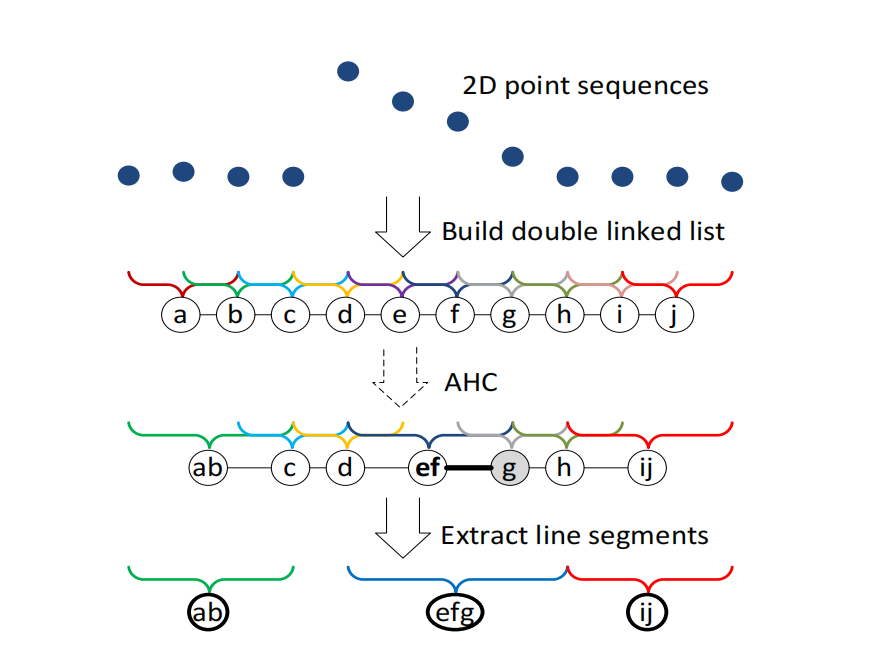
   图 3. 线性回归算法

• 蓝色点表示二维点。
• 用字母标记的圆圈表示链表中的节点。
• 方括号表示节点所代表的点集合。
• 粗线表示将节点 g 与其左邻居 ef 合并后的线拟合 MSE 小于将其与右邻居 h 合并的 MSE。

如果最小合并 MSE 大于预定义阈值（通常根据传感器噪声特性确定），则取消合并，节点 ggg 可被提取为一条线段。

使用 二叉堆 找最小 MSE 节点时，该算法可实现 对数线性时间复杂度 O(nlog⁡n)O(n \log n)O(nlogn)，其中 nnn 为序列中的点数。

注意，通过应用积分图（integral images）的思想，如文献 [11,23] 所用，合并两个节点并计算线拟合 MSE 可在 常数时间 完成。

---

B. 推广到 3D 的差异

受到点序列中邻域信息使用的启发，我们希望将二维线回归推广到 组织化点云中的三维平面提取，其中邻域信息由二维索引存储。然而，这一推广并非易事，主要有两个区别：

1 节点不重叠

与线回归不同，初始节点（以及在合并过程中产生的任意两个节点）不能有相同的点 ，即对于任意两个节点 Bs,Bt⊂FB_s, B_t \subset FBs,Bt⊂F，必须满足

Bs∩Bt=∅. B_s \cap B_t = \emptyset. Bs∩Bt=∅.

这是因为经过多次合并后，属于某个节点 BsB_sBs 的三维点会形成不规则形状，而不再保持其在图像空间中的初始矩形形状，如图 2(b) 所示。因此，如果允许不同节点包含相同点，即使借助积分图，也难以高效处理节点合并时的重叠点。

而在线回归中，合并相邻线段仍然只需记录起点和终点索引，因此允许节点重叠是可行的。值得注意的是，节点重叠的好处是可以自动检测线段边界：包含不同线段点的节点倾向于产生较大的线拟合 MSE（例如图 3 中的节点 c、d、h），其合并尝试会被延迟并最终被拒绝。

我们算法中要求节点不重叠，因此失去了自动检测平面边界的优势。我们将在 第 6.3-A 节 描述如何通过初始化步骤去除坏节点来克服这一劣势，并在 第 6.4 节描述一种像素级的区域生长算法以精细化平面边界。

---

2 合并尝试次数

在线回归中，将节点与其邻居合并是 常数时间操作，最多只需尝试两个方向（左或右邻居）。

而在我们的情况中，合并尝试次数更多：

• 初始节点最多连接 4 个邻居形成图结构；
• 经过多次合并后，节点可能与更多邻居相连。

我们将在 第 6.3-B 节 实验分析算法中平均合并尝试次数，并展示在实际中它保持较小。因此，合并步骤仍可在 常数时间 完成，使得整体复杂度与线回归相似，为 O(nlog⁡n)O(n \log n)O(nlogn)。

---

6.2 快速粗略分割 (FAST COARSE SEGMENTATION)

我们的快速平面提取算法主要由三个步骤组成，如图 2 和算法 1 所示：

1. 算法首先初始化一个图结构；
2. 然后执行 自底向上的层次聚类 (AHC, Agglomerative Hierarchical Clustering) 提取粗平面；
3. 最后进行精细化。
   

如果应用只需要 平面区域的粗略分割 ，例如在点云中检测物体，则可以跳过最后的精细化步骤，这样在 640×480640 \times 480640×480 点的情况下，帧率可超过 50Hz。

首先明确符号：

• FFF 表示一帧完整的组织化点云，包含 MMM 行 NNN 列点。
• B,CB, CB,C 分别表示粗分割和平面精细分割，即 Bk/ClB_k / C_lBk/Cl 是一个 平面片段 ，由一组 3D 点 pi,jp_{i,j}pi,j 组成。
• Π,Π0\Pi, \Pi_0Π,Π0 分别为 B,CB, CB,C 对应的平面方程集合。
• 注意，图 GGG 的每个节点 vvv 是一组 3D 点，每条无向边 uvuvuv 表示图像空间中平面片段 u,vu, vu,v 的邻域关系。

---

A. 图初始化 (Graph Initialization)

如 第 6.2-B 节 所述，我们算法要求 初始化节点不重叠（见算法 2 第 3--5 行）。

• 该步骤在图像空间中将点云均匀划分为大小为 H×WH \times WH×W 的初始节点集合。
• 这种要求导致算法失去自动检测平面边界的优势。

为了在 AHC 下正确分割平面，我们从图中移除以下类型的节点及对应边，如图 4 所示：

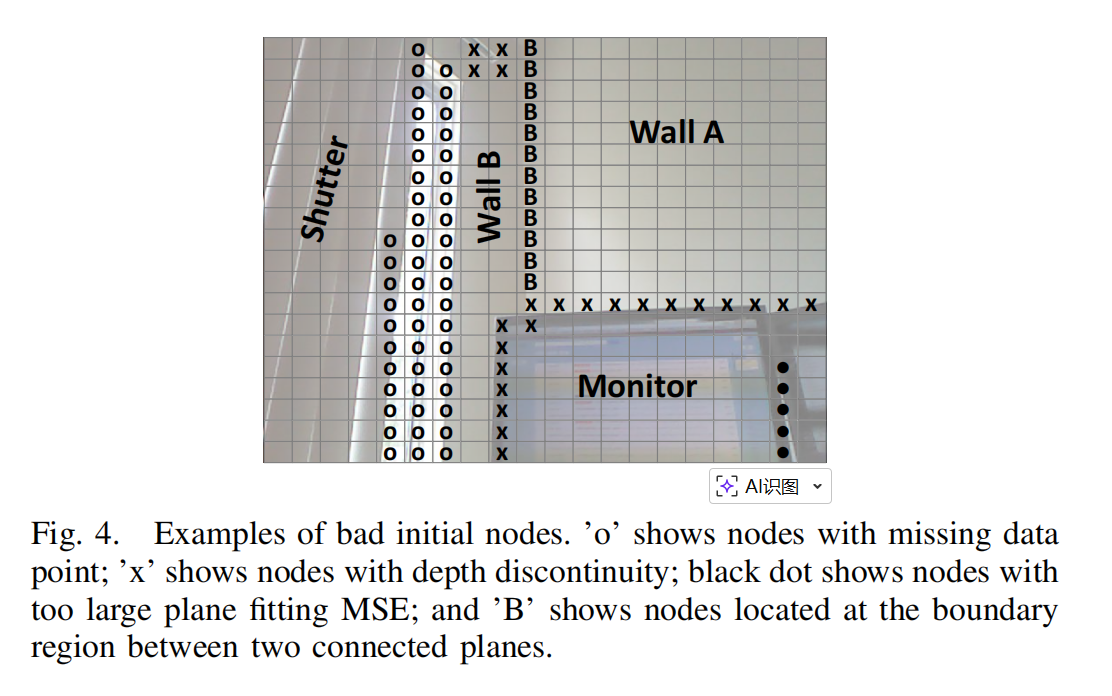
1. 高 MSE 节点：非平面区域导致平面拟合 MSE 较高，直接移除。
2. 包含缺失数据的节点：由于传感器限制，场景部分区域可能未被正确感知，导致数据缺失（例如百叶窗后面的玻璃窗）。
3. 包含深度不连续的节点：这些节点包含两组在 3D 中不接近但在图像空间接近的点（通常一个表面部分遮挡另一个表面，例如显示器遮挡墙壁）。如果对该节点执行 PCA 拟合平面，拟合平面会几乎平行于视线方向，因此 MSE 仍然较小。将该"异常"节点与邻居节点合并，会对平面拟合结果产生不良影响，这是最小二乘法过度加权异常值的已知问题。
4. 位于两平面边界的节点：这些节点包含两组在 3D 中接近但位于不同平面的点（例如房间角落），若合并到其中一个平面，会降低平面拟合精度。

算法 2 中的 REJECTNODE 和 REJECTEDGE 函数用于减少这四类不良初始节点的影响：

• REJECTNODE：移除前三类不良节点（及其包含的点）；
• REJECTEDGE：减轻第四类节点的影响。

值得注意的是，这种不重叠"缺点"的一个收获是 避免了对每个点计算法向量。

• 初始化步骤可视作将节点内部所有点视作具有相同平面法向量。
• 这是我们相比其他方法速度提升的重要原因------其他方法往往在每个点的法向量估计上花费大量时间。
  

---

B. 自底向上的层次聚类 (Agglomerative Hierarchical Clustering)

如 算法 3 所示，我们的 AHC 与线回归几乎相同，但操作对象是 图而非双向链表。

1. 首先构建 最小堆，高效查找当前平面拟合 MSE 最小的节点。

2. 重复以下步骤：

   • 找到图中当前平面拟合 MSE 最小的节点 vvv；
   • 将其与邻居节点 ubestu_{\text{best}}ubest 合并，使合并后的 MSE 最小（回忆：图中每个节点是一组点，合并 MSE 为两组点的联合平面拟合 MSE）。

3. 若最小合并 MSE 超过预定义阈值 TMSET_{\text{MSE}}TMSE（不一定是固定参数，见第 6.3-C 节说明），则找到并提取一个平面片段 vvv；

4. 否则，将合并节点 umergeu_{\text{merge}}umerge 通过边收缩加入图中。

如 第 6.2-B 节 所述，我们算法要求的合并尝试次数比线回归多，但仍然高效，实际聚类过程可在 O(nlog⁡n)O(n \log n)O(nlogn) 时间内完成。

• 图 5 显示了每帧 AHC 平均合并尝试次数。
• 不论初始节点大小（即初始节点数），平均尝试次数保持较小。
• 原因：算法 2 构建的图为 平面图。根据图论，平面图平均节点度严格小于 6。
• 我们的初始图为平面图，边收缩合并节点不会改变平面性，因此 AHC 过程中平均节点度始终小于 6。
• 大片段的平面拟合 MSE 大于小片段（假设误差服从同一高斯分布），AHC 倾向平衡所有片段的大小，先增长 MSE 最小的节点，再切换到其他较小节点，避免单个大节点过度增长。

因此，算法 3 第 6--21 行可在 常数时间 完成，O(nlog⁡n)O(n \log n)O(nlogn) 复杂度仅来自维护最小堆。

---

C. 实现细节 (Implementation Details)

为了提高快速粗略分割的速度与精度，有几个实现细节：

1. 并查集 (Disjoint Set)

   • 用于跟踪每个初始节点 vi,jv_{i,j}vi,j 的点成员关系。

2. 节点统计量

   • 类似线回归，所有节点维护所属点的一阶和二阶统计量：

   ∑xi,j,∑yi,j,∑zi,j,∑xi,j2,∑yi,j2,∑zi,j2,∑xi,jyi,j,∑yi,jzi,j,∑zi,jxi,j \sum x_{i,j}, \quad \sum y_{i,j}, \quad \sum z_{i,j}, \quad \sum x_{i,j}^2, \quad \sum y_{i,j}^2, \quad \sum z_{i,j}^2, \quad \sum x_{i,j} y_{i,j}, \quad \sum y_{i,j} z_{i,j}, \quad \sum z_{i,j} x_{i,j} ∑xi,j,∑yi,j,∑zi,j,∑xi,j2,∑yi,j2,∑zi,j2,∑xi,jyi,j,∑yi,jzi,j,∑zi,jxi,j

   • 这样合并两个节点并通过 PCA 计算平面方程和 MSE 可在 常数时间完成。

3. 深度不连续检测

   • REJECTNODE 函数中判断深度不连续依赖传感器噪声特性。
   • 对 Kinect 传感器，使用文献 [23] 与 PCL 建议函数：

   f(pa,pb)={1,if ∣za−zb∣>2α(∣za∣+0.5) 0,otherwise f(p_a, p_b) = \begin{cases} 1, & \text{if } |z_a - z_b| > 2\alpha(|z_a| + 0.5) \ 0, & \text{otherwise} \end{cases} f(pa,pb)={1,if ∣za−zb∣>2α(∣za∣+0.5) 0,otherwise

   • 单位为毫米，参数 α\alphaα 取 0.01∼0.020.01 \sim 0.020.01∼0.02。

4. 平面片段提取阈值 TMSET_{\text{MSE}}TMSE

   • 与传感器相关。
   • 对 Kinect，采用文献 [24] 的公式：

   TMSE=(σz2+ϵ)2 T_{\text{MSE}} = (\sigma_z^2 + \epsilon)^2 TMSE=(σz2+ϵ)2

   • 其中 σ=1.6×10−6\sigma = 1.6 \times 10^{-6}σ=1.6×10−6，ϵ∈[3,8]\epsilon \in [3, 8]ϵ∈[3,8]。
   • 角度阈值 TANGT_{\text{ANG}}TANG 也可随深度调整。

5. 初始节点形状

   • 节点应接近正方形，即 W≈HW \approx HW≈H。
   • 若使用条状节点（W≫HW \gg HW≫H 或 H≫WH \gg WH≫W），PCA 拟合平面法向会错误，通常接近视线方向，导致 AHC 分割失败。

---

6.3. 分割精细化 (SEGMENTATION REFINEMENT)

对于许多应用场景，上一节得到的 粗平面分割 可能不够精确，尤其是当应用需要 平面边界信息 或对 平面方程精度 有较高要求时。因此，我们对粗分割 BBB 进行 精细化处理。

粗分割中常见的三类问题，如图 6 所示：

1. 锯齿状 (Sawtooth)：通常出现在两个相连平面的边界处。
2. 未使用的数据点 (Unused Data Points)：通常出现在遮挡边界或缺失数据节点处。
3. 过度分割 (Over-Segmentation)：通常出现在两个物体的遮挡边界之间。

• 锯齿状会导致少量异常点被包含在平面估计中；
• 未使用数据点和过度分割会导致有效内点减少。
• 所有这些问题都会产生 不准确的平面边界 ，并稍微降低平面方程估计的精度。
  

---

解决方案 (Algorithm 4)

1. 锯齿状处理

   • 锯齿状问题几乎总是在 BBB 的边界区域出现。
   • 对每个平面片段的边界区域进行 腐蚀 (erosion) 可以有效去除锯齿（算法第 5--13 行）。

2. 像素级区域生长 (Pixel-wise Region Growing)

   • 从所有新的边界点开始，对未使用的数据点进行分配：

     • 将每个未使用点分配到之前提取的最近平面。

   • 在区域生长过程中，发现每个平面 BkB_kBk 的 4-邻域 ，形成一个新的图 G′G'G′（算法第 14--27 行）。

3. 修复过度分割

   • 对 G′G'G′（通常小于 30 个节点）再次应用 AHC ，可以解决过度分割问题（算法第 28 行）。
     

---

总结：

• 该精细化方法通过 边界腐蚀 + 像素级区域生长 + 小规模 AHC，解决了粗分割中的三类主要问题。
• 可以得到 更准确的平面边界 和 更精确的平面方程，适用于需要高精度的 SLAM 或 3D 感知任务。

---

7. 算法优势（Advantages）

1. 实时性高：640×480 点云 >35 Hz
2. 精度高：与最先进算法可比
3. 无需每点法线估计 → 大幅减少计算量
4. 动态边权 → 合并顺序自适应
5. 适合有序点云：Kinect、ToF、结构光等

---

8. 算法流程总结（Flowchart）

1. 输入有序点云 FFF
2. Graph Initialization → 初始节点 VVV，边 EEE
3. AHC 聚合 → 粗平面 BBB
4. Segmentation Refinement → 精细平面 CCC
5. 输出平面集合 CCC 及平面方程 Π0\Pi_0Π0

---

9. 参考文献（Selected References）

1. O. Faugeras, "Three-Dimensional Computer Vision," MIT Press, 1993.
2. RANSAC-based plane extraction: Fischler & Bolles, 1981.
3. Region growing: Hahnel et al., 2003
4. PCA-based plane fitting: Holz et al., 2012
5. Fast plane extraction with line regression ideas: Geogiev et al., 2010
6. Graph-based segmentation: Enjarini et al., 2014

---