大家好，我是爱酱。继前几篇介绍了层次聚类、K均值聚类和密度聚类之后，本篇我们聚焦于另一种强大的聚类算法------高斯混合模型（GMM）。GMM是一种基于概率的软聚类方法，能够为每个样本点计算属于各个簇的概率，适合复杂数据的建模。本文将系统介绍GMM的原理、数学表达、实际案例流程及Python代码实现，加上大量公式给出，方便你直接用于技术文档和学习。
注：本文章含大量数学算式、详细例子说明及代码演示，大量干货，建议先收藏再慢慢观看理解。新频道发展不易，你们的每个赞、收藏跟转发都是我继续分享的动力！
高斯混合模型（GMM）三大核心内容
我发现很多人都会弄混乱混合模型概率密度函数、多元高斯分布概率密度函数 和期望最大化（EM）算法这三个概念。实际上，高斯混合模型（GMM）其实是指GMM包含三大核心组成部分 ，不是说有三种完全不同的聚类算法，而是说GMM的数学实现分为三大模块/步骤：
-
混合模型概率密度函数：这是GMM对整体数据分布的建模方式，用来表达"所有数据点的分布是多个高斯分布的加权和"。
-
多元高斯分布概率密度函数：这是GMM中每个簇（高斯分量）本身的概率密度表达式，用来计算每个点在每个簇下的概率。
-
期望最大化（EM）算法：这是GMM参数估计的优化算法，分为E步和M步，反复迭代求解参数（均值、协方差、权重）。
它们不是三种互相独立的聚类方法，而是GMM的三个核心"环节"或"步骤"。
GMM聚类的简化实际流程：
-
用混合模型概率密度函数描述整体分布，
-
用多元高斯分布概率密度函数计算每个点的概率，
-
用EM算法迭代优化参数，
-
最终得到聚类结果。
所以，实际案例流程只能是"GMM聚类的整体流程"，而不是分别独立跑三种聚类方法。
一、混合模型概率密度函数（Mixture Model Probability Density Function）
GMM假设数据分布为多个高斯分布的加权和：
-
：簇数
-
-
案例解释
假设我们有2个簇（），每个簇的均值、协方差和权重分别为
-
-
则任意点的概率密度就是两个高斯分布的加权和。
二、多元高斯分布概率密度函数（Multivariate Gaussian Probability Density Function/ Multivariate Gaussian PDF）
单个高斯分布的概率密度为：
-
-
案例解释
对于二维点，
，
为
协方差矩阵，上式可直接代入计算。
三、期望最大化（EM）算法（Expectation-Maximization Algorithm）
GMM的参数用EM算法迭代估计：
1. 初始化
随机设定、
、
。
2. E步（Expectation）
计算每个点属于每个簇的后验概率（责任度）：
3. M步（Maximization）
根据更新参数：
4. 重复E步和M步，直到参数收敛
四、完整案例流程
数据
| 点 | ||
|---|---|---|
| A | 1 | 2 |
| B | 2 | 1 |
| C | 1 | 4 |
| D | 10 | 2 |
| E | 12 | 3 |
| F | 11 | 4 |
步骤
-
初始化
设
-
E步
对每个点，分别计算其在两个高斯分布下的概率密度
-
M步
用
-
重复E步和M步
迭代直到参数收敛。
-
最终结果
每个点属于每个簇的概率
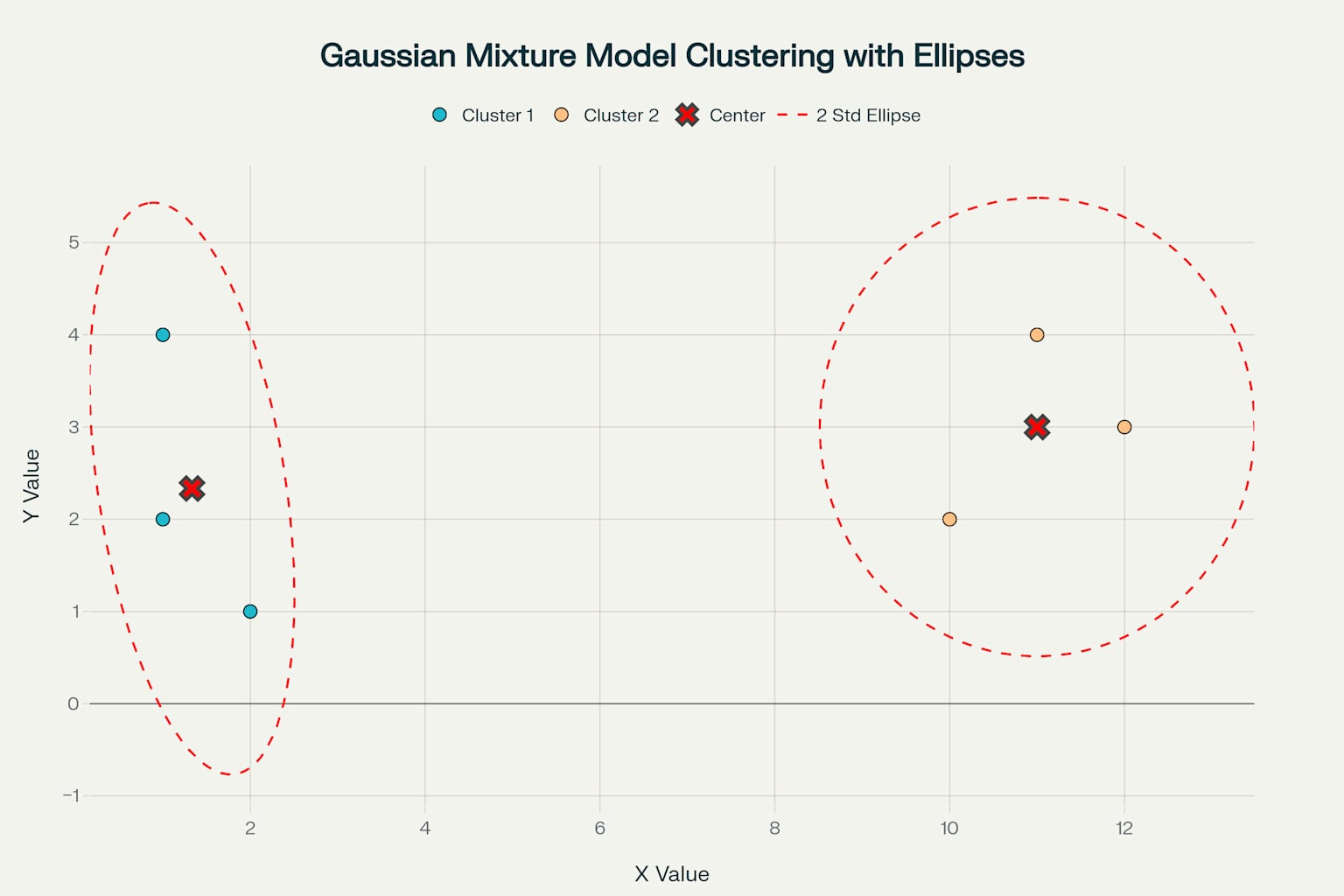
五、Python代码实现
注：记得要先 pip install scikit-learnLibrary喔～
python
import numpy as np
import matplotlib.pyplot as plt
from sklearn.mixture import GaussianMixture
from matplotlib.patches import Ellipse
def plot_gmm_clusters(X, gmm, std_multiplier=4):
labels = gmm.predict(X)
plt.figure(figsize=(8,6))
plt.scatter(X[:, 0], X[:, 1], c=labels, cmap='viridis', s=100, label='Data points')
plt.scatter(gmm.means_[:, 0], gmm.means_[:, 1], c='red', marker='x', s=200, label='Cluster centers')
ax = plt.gca()
for i in range(gmm.n_components):
mean = gmm.means_[i]
covar = gmm.covariances_[i]
# Eigen decomposition for ellipse axes
v, w = np.linalg.eigh(covar)
order = v.argsort()[::-1]
v = v[order]
w = w[:, order]
# Angle of ellipse
angle = np.degrees(np.arctan2(w[1, 0], w[0, 0]))
# Width and height: std_multiplier standard deviations
width, height = std_multiplier * np.sqrt(v)
ell = Ellipse(mean, width, height, angle=angle, edgecolor='red', facecolor='none', linestyle='--', linewidth=2)
ax.add_patch(ell)
plt.title(f'Gaussian Mixture Model Clustering with {std_multiplier} Std Ellipses')
plt.xlabel('X')
plt.ylabel('Y')
plt.legend()
plt.grid(True)
plt.show()
# 示例数据
X = np.array([[1,2],[2,1],[1,4],[10,2],[12,3],[11,4]])
# 建立GMM模型，设定簇数为2
gmm = GaussianMixture(n_components=2, covariance_type='full', random_state=0)
gmm.fit(X)
# 调用绘图函数，std_multiplier=4确保几乎所有点都被椭圆覆盖
plot_gmm_clusters(X, gmm, std_multiplier=4)
# 输出每个点属于各簇的概率
probs = gmm.predict_proba(X)
for i, p in enumerate(probs):
print(f"Point {i} probabilities: {p}")六、模型选择指标（BIC、AIC）确定簇数
在实际应用中，GMM需要用户指定簇数（n_components），但真实数据的最佳簇数往往未知。为此，统计学上常用AIC（Akaike Information Criterion）和BIC（Bayesian Information Criterion）来辅助选择最优模型。
1. AIC（Akaike信息准则）
其中 是模型参数数量，
是最大似然估计下的似然值。AIC越小，模型越优。
2. BIC（贝叶斯信息准则）
其中 是样本数。BIC同样越小越好，但对模型复杂度惩罚更强。
3. 实际用法
-
训练不同簇数的GMM模型，分别计算AIC和BIC。
-
选择AIC/BIC最小的模型作为最优簇数
七、GMM的优缺点
优点
-
软聚类，给出每个点属于各簇的概率
-
能拟合复杂的椭球形簇，适合多样分布
-
适合高维数据，参数灵活
缺点
-
对初始参数敏感，可能陷入局部最优
-
计算复杂度较高，尤其是协方差矩阵估计
-
需预先指定簇数
八、总结
高斯混合模型是一种强大的概率聚类方法，适合复杂数据的软分配和多样簇形建模。通过EM算法迭代估计参数，GMM能为每个样本点提供属于各簇的概率，提升聚类的灵活性和解释力。实际应用中，需结合模型选择指标（如BIC、AIC）确定簇数，并关注初始化和参数调优。希望本篇内容能帮助你深入理解GMM的数学原理与实操流程。
谢谢你看到这里，你们的每个赞、收藏跟转发都是我继续分享的动力。
如需进一步案例、代码实现或与其他聚类算法对比，欢迎留言交流！我是爱酱，我们下次再见，谢谢收看！