
| 🔭 个人主页: 散峰而望 |
|---|
《C语言:从基础到进阶》《编程工具的下载和使用》《C语言刷题》《算法竞赛从入门到获奖》《人工智能》《AI Agent》
愿为出海月,不做归山云
🎬博主简介



【算法竞赛】高精度运算深度解析与优化
前言
算法竞赛中经常需要处理超出标准数据类型范围的整数运算,例如大数阶乘、斐波那契数列的大项计算或密码学相关题目。标准数据类型如 int 或 long long 的存储范围有限,无法直接处理上百位的数字运算。高精度运算通过模拟人工计算过程,将大数拆分为数组或字符串逐位处理,成为解决此类问题的核心方法。
高精度
当数据的值特别大,各种类型都存不下的时候,此时就要用高精度算法来计算加减乘除:
- 先用字符串读入这个数,然后用数组逆序存储该数的每一位;
- 利用数组,模拟加减乘除运算的过程。
高精度算法本质上还是模拟算法,用代码模拟小学列竖式计算加减乘除的过程。
之所以用数组逆序存储该数的每一位 ,是因为我们计算的是从个位开始,而逆序正好是从下标 0 位开始,模拟最低位到最高位*。同时处理进位时,正序的话,进位不知道往什么位置进位。
1. 高精度加法
算法原理:
模拟小学「列竖式」计算「两数相加」的过程。
- 用字符串读入数据;
- 将字符串的每一位拆分,逆序放在数组中;
cpp
x = " 4 3 9 "
下标 0 1 2
int a[] = [9, 3, 4]
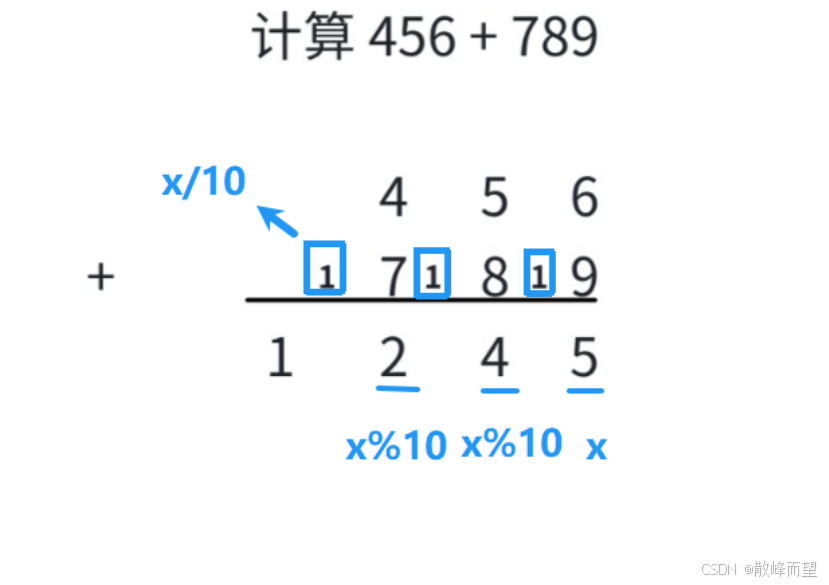
下标 0 1 2- 模拟列竖式计算的过程:
a. 对应位累加 -->x
b. 处理进位 -->x / 10
c. 处理余数 -->x % 10
- 处理结果的位数。
核心代码:
cpp
void add(int c[], int a[], int b[])
{
for(int i = 0; i < lc; i++)
{
c[i] += a[i] + b[i];
c[i + 1] = c[i] / 10;
c[i] %= 10;
}
if(c[lc]) lc++;
}参考代码:
cpp
#include <iostream>
using namespace std;
const int N = 1e6 + 10;
int a[N], b[N], c[N];
int la, lb, lc;
void add(int c[], int a[], int b[])
{
for(int i = 0; i < lc; i++)
{
c[i] += a[i] + b[i];
c[i + 1] = c[i] / 10;
c[i] %= 10;
}
if(c[lc]) lc++;
}
int main()
{
string x, y;
cin >> x >> y;
//拆分每一位,逆序放在数组中
la = x.size();
lb = y.size();
lc = max(la, lb);
//先指定lc的最大的数范围后,如果超过就再加
for(int i = 0; i < la; i++) a[la - 1 - i] = x[i] - '0';
for(int i = 0; i < lb; i++) b[lb - 1 - i] = y[i] - '0';
//模拟加法过程
add(c, a, b);
//输出
for(int i = lc - 1; i >= 0; i--)
{
cout << c[i];
}
return 0;
} 2. 高精度减法
算法原理:
模拟小学「列竖式」计算「两数相减」的过程。
- 用字符串读入数据;
- 判断两个数的大小,让较大的数在前。注意字典序 vs 数的大小:
a. 位数相等:按字典序比较;
b. 位数不等:按照字符串的长度比较。
即先比较长度再比较字典序,不然会出现下面这种情况
cpp
数: 101 > 99
字符串: "101" < "99"- 将字符串的每一位拆分,逆序放在数组中;
- 模拟列竖式计算的过程:
a. 对应位求差;
b. 处理借位; - 处理前导零:因为减数完位数可能会往后退,比如十位退到个位,此时在十位的没有存储其他东西,就要把此处的空间释放掉。
核心代码:
cpp
void sub(int c[], int a[], int b[])
{
for(int i = 0; i < lc; i++)
{
c[i] += a[i] - b[i]; // 对应位相减,然后处理借位
if(c[i] < 0)
{
c[i + 1] -= 1; // 借位
c[i] += 10;
}
}
// 处理前导零
while(lc > 1 && c[lc - 1] == 0) lc--;
}参考代码:
cpp
#include <iostream>
using namespace std;
const int N = 1e6 + 10;
int a[N], b[N], c[N];
int la, lb, lc;
// 比大小
bool cmp(string& x, string& y)
{
// 先比较长度
if(x.size() != y.size()) return x.size() < y.size();
// 再按照字典序的方式比较
return x < y;
}
void sub(int c[], int a[], int b[])
{
for(int i = 0; i < lc; i++)
{
c[i] += a[i] - b[i]; // 对应位相减,然后处理借位
if(c[i] < 0)
{
c[i + 1] -= 1; // 借位
c[i] += 10;
}
}
// 处理前导零
while(lc > 1 && c[lc - 1] == 0) lc--;
}
int main()
{
string x, y; cin >> x >> y;
// 比大小
if(cmp(x, y))
{
swap(x, y);
cout << '-';
}
//拆分每一位,然后逆序放在数组中
la = x.size(); lb = y.size(); lc = max(la, lb);
for(int i = 0; i < la; i++) a[la - i - 1] = x[i] - '0';
for(int i = 0; i < lb; i++) b[lb - i - 1] = y[i] - '0';
//模拟减法的过程
sub(c, a, b); // c = a - b
//输出
for(int i = lc - 1; i >= 0; i--) cout << c[i];
return 0;
}3. 高精度乘法
算法原理:
无进位相乘再相加:
- 还是「列竖式」,但是每一位相乘的时候不考虑进位,直接把乘的结果放在对应位上;
- 等到所有对应位置「乘完」并且「累加完」之后,「统一处理进位」。
如下图所示:

即可理解为下标 + 下标 = 对应下标相乘位置 => c[i + j] += a[i] * b[j]:
- 0 下标和 0 下标相乘在 0 下标位置,和 1 下标相乘在 1 下标位置,和 2 下标相乘在 2 下标位置
- 1 下标和 0 下标相乘在 1 下标位置,和 1 下标相乘在 2 下标位置,和 2 下标相乘在 3 下标位置
- 2 下标和 0 下标相乘在 2 下标位置,和 1 下标相乘在 3 下标位置,和 2 下标相乘在 4 下标位置
具体解法:
- 用字符串读入数据;
- 将字符串的每一位拆分,逆序放在数组中;
- 模拟无进位相乘再相加的过程:
a. 对应位求乘积;
b. 乘完之后处理进位;
c. 处理余数; - 处理前导零。
核心代码:
cpp
void mul(int c[], int a[], int b[])
{
// 无进位相乘,然后相加
for(int i = 0; i < la; i++)
{
for(int j = 0; j < lb; j++)
{
c[i + j] += a[i] * b[j];
}
}
// 处理进位
for(int i = 0; i < lc; i++)
{
c[i + 1] += c[i] / 10;
c[i] %= 10;
}
// 处理前导零
while(lc > 1 && c[lc - 1] == 0) lc--;
}参考代码:
cpp
#include <iostream>
using namespace std;
const int N = 1e6 + 10;
int a[N], b[N], c[N];
int la, lb, lc;
void mul(int c[], int a[], int b[])
{
// 无进位相乘,然后相加
for(int i = 0; i < la; i++)
{
for(int j = 0; j < lb; j++)
{
c[i + j] += a[i] * b[j];
}
}
// 处理进位
for(int i = 0; i < lc; i++)
{
c[i + 1] += c[i] / 10;
c[i] %= 10;
}
// 处理前导零
while(lc > 1 && c[lc - 1] == 0) lc--;
}
int main()
{
string x, y; cin >> x >> y;
//拆分每一位,逆序放在数组中
la = x.size(); lb = y.size(); lc = la + lb;
for(int i = 0; i < la; i++) a[la - 1 - i] = x[i] - '0';
for(int i = 0; i < lb; i++) b[lb - 1 - i] = y[i] - '0';
//模拟乘法的过程
mul(c, a, b); // c = a * b
//输出
for(int i = lc - 1; i >= 0; i--) cout << c[i];
return 0;
}4. 高精度除法
算法原理:
模拟小学「列竖式」计算「两数相除」的过程(注意:我们这里是「高精度 ÷ 低精度」,而「高精度 ÷ 高精度」题目比较少见,其模拟方式是用减法方法,可以下去自行了解)
定义一个指针 i 从「高位」遍历被除数,一个变量 t 标记当前「被除的数」,记除数是 b
- 更新一个当前被除的数
t = t × 10 + a[i] t / b表示这一位的商,t % b表示这一位的余数- 用 t 记录这一次的余数,遍历到下一位的时候重复上面的过程
被除数遍历完毕之后,t 里面存的就是余数,但是商可能存在前导 0 ,注意清空。
核心代码:
cpp
void sub(int c[], int a[], int b)
{
LL t = 0; // 标记每次除完之后的余数
for(int i = la - 1; i >= 0; i--)
{
// 计算当前的被除数
t = t * 10 + a[i];
c[i] = t / b;
t %= b;
}
// 处理前导 0
while(lc > 1 && c[lc - 1] == 0) lc--;
}参考代码:
cpp
#include <iostream>
using namespace std;
const int N = 1e6 + 10;
typedef long long LL;
int a[N], b, c[N];
int la, lc;
void sub(int c[], int a[], int b)
{
LL t = 0; // 标记每次除完之后的余数
for(int i = la - 1; i >= 0; i--)
{
// 计算当前的被除数
t = t * 10 + a[i];
c[i] = t / b;
t %= b;
}
// 处理前导 0
while(lc > 1 && c[lc - 1] == 0) lc--;
}
int main()
{
string x; cin >> x >> b;
la = x.size();
for(int i = 0; i < la; i++) a[la - 1 - i] = x[i] - '0';
// 模拟除法的过程
lc = la;
sub(c, a, b); // c = a / b
for(int i = lc - 1; i >= 0; i--) cout << c[i];
return 0;
}结语
高精度运算在算法竞赛中占据重要地位,尤其在处理大整数运算时不可或缺。通过模拟手工计算的方法,高精度加法、减法、乘法和除法能够突破语言原生数据类型的限制,实现任意位数的精确计算。
掌握高精度运算的核心在于理解逐位处理与进位借位的逻辑,并优化存储与计算率。在实际竞赛中,灵活运用高精度算法可解决大数阶乘、大数取模、高精度浮点运算等复杂问题。
进一步优化高精度运算可结合快速傅里叶变换(FFT)加速乘法,或采用压位存储减少计算次数。持续练习与深入理解高精度算法,能显著提升解决复杂数学问题的力。
愿诸君能一起共渡重重浪,终见缛彩遥分地,繁光远缀天。
