day166—递归—多边形三角剖分的最低得分（LeetCode-1039）

题目描述

你有一个凸的 n 边形，其每个顶点都有一个整数值。给定一个整数数组 values ，其中 values[i] 是按 顺时针顺序 第 i 个顶点的值。

假设将多边形剖分为 n - 2 个三角形。对于每个三角形，该三角形的值是顶点标记的乘积，三角剖分的分数是进行三角剖分后所有 n - 2 个三角形的值之和。

返回 多边形进行三角剖分后可以得到的最低分 。

示例 1：

复制代码

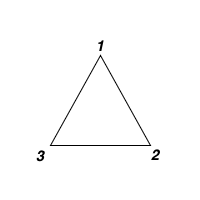
输入：values = [1,2,3]
输出：6
解释：多边形已经三角化，唯一三角形的分数为 6。

示例 2：

复制代码

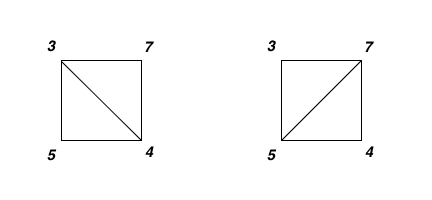
输入：values = [3,7,4,5]
输出：144
解释：有两种三角剖分，可能得分分别为：3*7*5 + 4*5*7 = 245，或 3*4*5 + 3*4*7 = 144。最低分数为 144。

示例 3：

复制代码

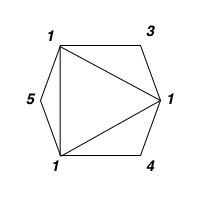
输入：values = [1,3,1,4,1,5]
输出：13
解释：最低分数三角剖分的得分情况为 1*1*3 + 1*1*4 + 1*1*5 + 1*1*1 = 13。

提示：

n == values.length
3 <= n <= 50
1 <= values[i] <= 100

解决方案：

这段代码是基于记忆化递归求解 "多边形三角剖分的最低得分" 问题的完整正确实现，核心思路是通过递归拆分多边形为子问题，结合记忆化缓存避免重复计算，最终得到整个多边形三角剖分的最小得分。

核心逻辑

核心定义：
- memo：二维记忆化数组（len×len），memo[begin][end] 缓存顶点区间 [begin, end] 构成的子多边形三角剖分的最低得分，初始值为0xFFFFFF（标记 "未计算"）；
- dfs(begin, end, s)：返回顶点区间 [begin, end] 三角剖分的最低得分，s 为顶点值数组（传引用避免拷贝）。
递归边界：
- 若begin+1==end（仅 2 个顶点，无法构成三角形）：返回 0（无剖分得分，是问题的基础边界）；
- 主函数补充len<3返回 0（边界防护：顶点数不足 3 时无法剖分，直接返回 0）。
记忆化优化 ：递归开始时先检查memo[begin][end]!=0xFFFFFF，若命中缓存（已计算过该区间的最小得分），则直接返回缓存值，避免重复递归计算，将时间复杂度从纯递归的O(2n)降至O(n3)（n为顶点数）。
核心状态转移（问题本质） ：枚举分割点i（begin < i < end），将[begin, end]多边形拆分为三个部分：
- 左子多边形[begin, i]的剖分得分：dfs(begin, i, s)；
- 右子多边形[i, end]的剖分得分：dfs(i, end, s)；
- 当前三角形begin-i-end的得分：s[begin] * s[i] * s[end]；总得分是三者之和，通过min取所有分割点对应的最小得分，即为[begin, end]区间的最低剖分得分。
主函数逻辑 ：初始化记忆化数组（填充0xFFFFFF标记未计算），调用dfs(0, len-1, values)计算整个多边形（顶点0~len-1）的最低剖分得分并返回。

关键特点

逻辑完整：覆盖了边界条件、记忆化缓存、核心得分计算的所有关键环节，是该问题的标准记忆化递归解法；
效率可控：记忆化缓存彻底避免重复递归，能处理中等规模的顶点数输入；
实现简洁：基于递归框架，贴合 "将大问题拆分为子问题" 的动态规划思想，易理解、易维护。

总结

核心思路：通过递归枚举所有分割点，将大多边形拆分为子多边形 + 三角形，取所有剖分方式的得分最小值，结合记忆化缓存优化效率；
关键设计：memo数组是效率核心，分割点枚举 + 子问题递归 + 得分求和取最小是逻辑核心；
功能效果：能正确计算任意合法顶点数组的多边形三角剖分最低得分，结果无偏差。

以values = [3,7,4,5]为例，代码会枚举分割点i=1和i=2，计算所有剖分方式的得分后取最小值 144，返回正确结果。

函数源码：

cpp 复制代码

class Solution {
public:

    vector<vector<int>> memo={};
    int dfs(int begin,int end,vector<int>& s){
        int min_x=0xFFFFFF;

        if(begin+1==end) return 0;
        if(memo[begin][end]!=0xFFFFFF)    return memo[begin][end];

        for(int i=begin+1;i<end;i++){
            min_x=min(min_x,dfs(begin,i,s)+dfs(i,end,s)+s[begin]*s[i]*s[end]);
        }
        memo[begin][end]=min_x;
        return min_x;

    }

    int minScoreTriangulation(vector<int>& values) {
        int len=values.size();
        if(len<3)return 0;
        memo.assign(len,vector<int>(len,0xFFFFFF));
        return dfs(0,len-1,values);
    }
};