
二维平面上的雷达跟踪的滤波,观测为测距+测角,基于匀速运动的EKF和RTS平滑。给出轨迹真值和各方法估计值、滤波前后与平滑后的结果对比、误差分析.
程序中雷达坐标、目标的轨迹、传感器噪声大小均可自行调整
文章目录
程序简介
程序为二维非线性目标跟踪仿真,利用距离--方位角(Range--Bearing)观测 对运动目标进行状态估计,并对比分析了**扩展卡尔曼滤波(EKF)与RTS 平滑(Rauch--Tung--Striebel Smoother)**在定位精度和统计性能上的差异。
目标采用二维匀速(CV)状态模型 ,状态向量定义为
x , y , v x , v y \] T \[x,y,v_x,v_y\]\^T \[x,y,vx,vy\]T,过程噪声由连续白噪声加速度模型离散化得到。观测模型为典型的非线性极坐标量测,即观测站到目标的距离和方位角,观测噪声分别服从零均值高斯分布。为真实反映工程场景,观测模型显式引入观测站空间位置,使量测方程对目标位置呈强非线性。
在滤波阶段,程序基于 EKF 完成前向递推,通过对非线性观测方程进行一阶线性化,构造雅可比矩阵并实现状态更新;在此基础上,引入RTS平滑算法,利用全时域量测信息对 EKF 结果进行后向修正,以进一步降低估计误差并提升轨迹连续性。
仿真给出了三类结果对比:
1. **直接观测反算结果**(极坐标量测直接转换为笛卡尔坐标)
2. **EKF 滤波估计结果**
3. **EKF + RTS 平滑结果**
程序从多角度对三种方法的性能进行了系统评估,包括:二维轨迹对比、定位误差时序曲线及 3σ 包络、一致性分析下的误差累积分布函数(CDF)、误差箱线图,以及 RMSE、最大误差、标准差和误差百分位数等统计指标。结果表明,在非线性距离--角度观测条件下,EKF 能显著抑制观测噪声,而 RTS 平滑在 EKF 基础上进一步提升了整体定位精度和误差稳定性。
## 运行结果
雷达所在位置、目标运动轨迹图像:
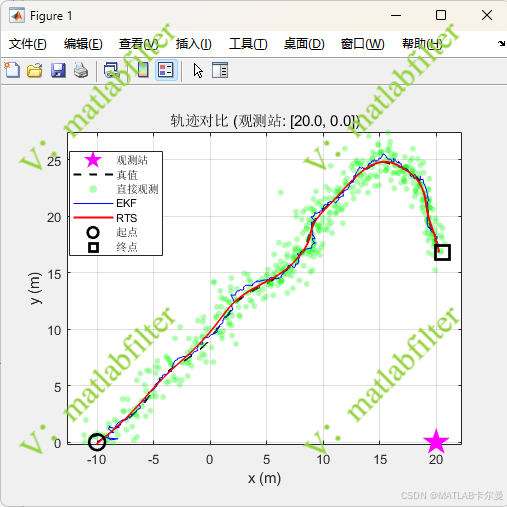
误差:
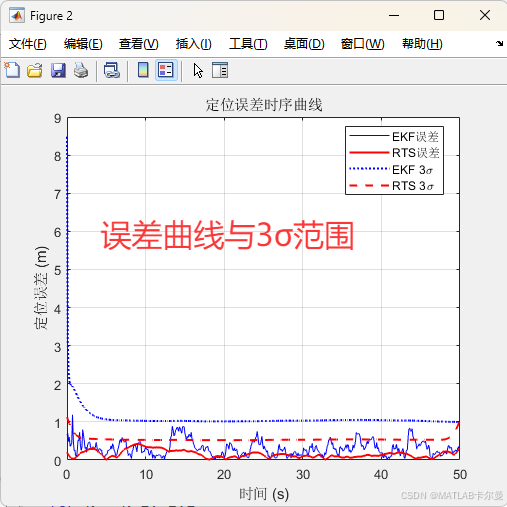
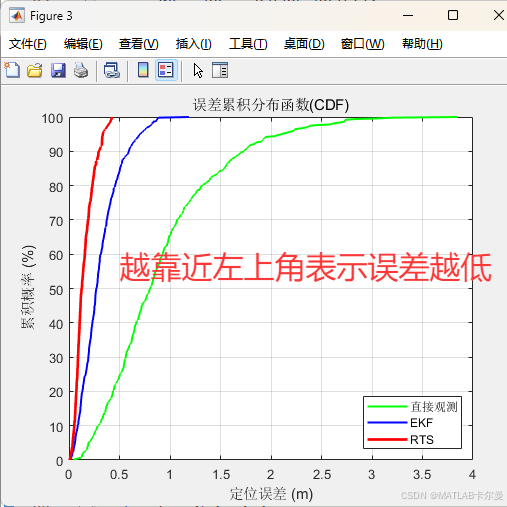
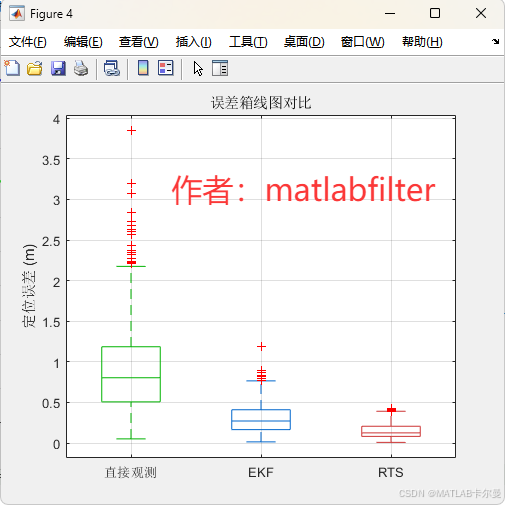
命令行输出的截图:
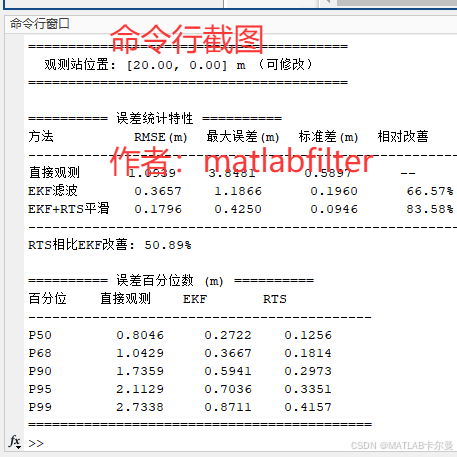
## MATLAB源代码
部分代码如下:
```matlab
%% 二维非线性目标跟踪,观测为距离+角度,EKF与RTS平滑
% 作者: matlabfilter
% 2026-01-16/Ver1
clear; clc; close all;
rng(0);
%% 参数设置
dt = 0.1;
T = 50;
N = T/dt;
t = (0:N-1)*dt;
% ===== 观测站位置(可调参数)
sensor_pos = [20; 0]; % 观测站位置 [x; y] (m)
% 状态转移(匀速模型)
F = [1 0 dt 0;
0 1 0 dt;
0 0 1 0;
0 0 0 1];
% 过程噪声
q = 0.5;
Q = q^2 * [dt^4/4 0 dt^3/2 0;
0 dt^4/4 0 dt^3/2;
dt^3/2 0 dt^2 0;
0 dt^3/2 0 dt^2];
% 观测噪声
sigma_r = 1; % 距离噪声 (m)
sigma_b = deg2rad(1); % 方位角噪声 (rad)
R = diag([sigma_r^2, sigma_b^2]);
%% 真实轨迹与观测
%% EKF 前向滤波
```
完整代码: