数据结构基础：B*树B+树的极致优化

1、B*树是什么？

B*树（B-star Tree） 是B+树的一个优化变种，由计算机科学家Donald Knuth 提出。它的核心目标是：在保持B+树优良特性的同时，进一步提高空间利用率。

B*树 = B+树 + 兄弟节点再分配 + 2/3最小填充度

它通过让相邻兄弟节点"互相帮忙"，推迟节点分裂的时机，从而让每个节点都更"满"。

从B树到B*树的演进历程

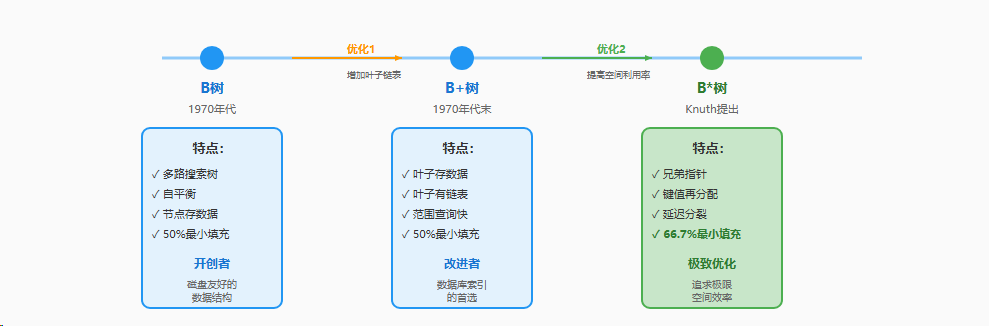
2、为什么需要B*树？

B树和B+树虽然优秀，但存在一个显著的问题：空间利用率不够高。

那么B*树是怎么解决这个问题的？

3、B*树解决的核心需求

1️⃣ 减少磁盘I/O（最重要）

• 问题：磁盘I/O是数据库性能的主要瓶颈，比内存操作慢10万倍
• 解决：更高的空间利用率意味着相同数据需要更少的节点，从而减少磁盘读写次数
• 效果：节省约25-30%的磁盘访问次数

2️⃣ 降低树高

• 问题：每增加一层树高，就多一次磁盘I/O
• 解决：节点更"满"意味着树更"矮胖"，查找路径更短
• 效果：存储相同数据量，树高可降低10-15%

3️⃣ 节省存储空间

• 问题：数据库规模动辄TB级，空间浪费代价高昂
• 解决：66.7%的最小填充率 vs 50%
• 效果：节省约25%的存储空间

4️⃣ 提高缓存命中率

• 问题：内存有限，不能缓存所有节点
• 解决：更少的节点意味着热点数据更容易被缓存
• 效果：缓存命中率提升20-30%

4、B*树的核心特性

B*树几乎总是 B+树 的一种变体，而不是经典B树的变体。

这意味着B*树继承了B+树所有关键的结构特性，然后在其上增加了更严格的填充规则。

4.1、核心特性

以下是B*树的核心结构特性总结：

• 根节点 ： 和B/B+树一样，如果根节点不是叶子，它必须至少有 2 个子节点。
• 内部节点 ： 非根的内部节点（索引节点）只存储键和指针。这是B*树的定义性规则 ：它必须有 ⌈2m/3⌉ 到 m 个子节点（B/B+树是 ⌈m/2⌉）。
• 叶子节点 ：
  • 结构： 继承B+树特性，所有叶子节点都在同一层，并且通过 双向链表 连接以支持高效的范围查询。
  • 内容： 存储 (键, 数据) 对。所有真实数据都只存在于叶子节点。
  • 填充率： 填充率也必须满足 ⌈2m/3⌉ 的下限。
• 对兄弟节点的依赖 (关键)： B树的所有核心操作（旋转、2-3分裂、3-2合并）都严重依赖于与兄弟节点的交互。因此，在B 树的 具体实现 中，非叶节点通常会包含一个直接的兄弟指针，以避免每次都通过父节点查找的开销。

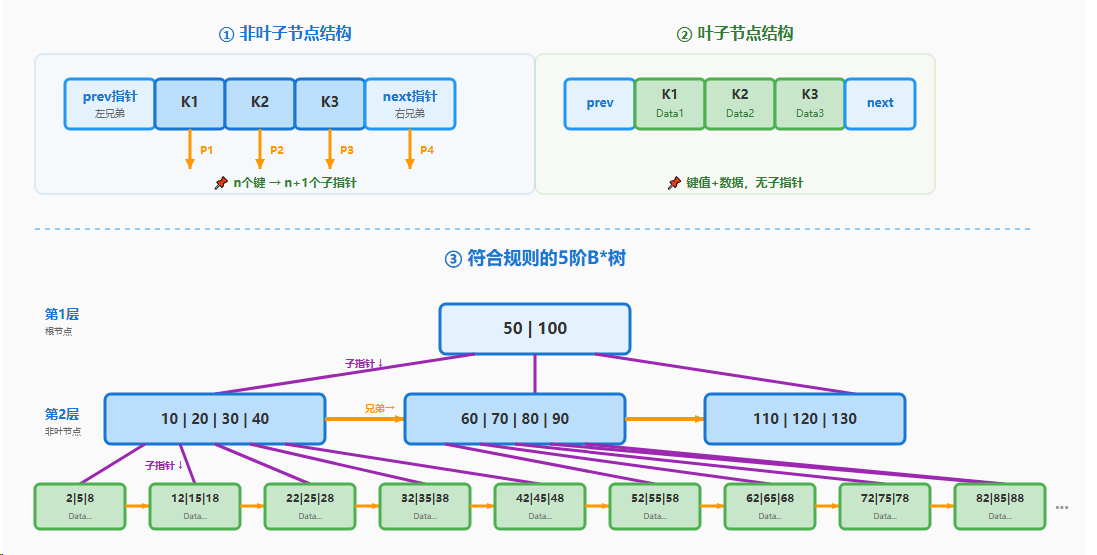
① 子指针

• 作用：连接父节点和子节点

• 方向：自上而下

• 特点：n个键 → n+1个子指针

② 兄弟指针

• 作用：实现再分配，推迟分裂

• 方向：水平横向

• 特点：双向链表，每层都有

③ 数据指针

• 作用：叶子节点存储实际数据

• 位置：仅在叶子节点

• 特点：键值对应数据记录

4.2、关键规则：2/3 填充率

为什么选择66.7%，2/3这个数字，这个 2/3 不是一个随意选择的数字，它是 B树 核心分裂策略 的 必然数学结果。B树的设计哲学是"延迟分裂"：当一个节点满了，它不像B树那样立即"1-2分裂"，而是尝试"2-3分裂"。

B*树规定，当一个节点（我们称之为 A）满了，它会拉上它旁边的兄弟节点（B）一起分裂。这个兄弟节点（B）此时也必须是满的（或者接近满的）。

这个策略被称为 "2-3分裂"，它的数学原理如下：

• B树（1-2分裂）： 1 个满节点（含新键）分裂成 2 个新节点。每个新节点大约 1/2 满。所以B树的下限是 1/2。
• B*树（2-3分裂）： 2 个满节点（加上父节点的1个分隔键和1个新键）合并后，重新分裂成 3 个新节点。

让我们来看一下"2-3分裂"的数学细节（这里以键的数量为例）：

1. 我们有 2个满节点 。一个满节点有 m-1 个键。总共 2 * (m-1) 个键。
2. 我们从父节点"借"来 1个分隔键。
3. 我们还要插入 1个新键。
4. 总键池 = (m-1) + (m-1) + 1 (父键) + 1 (新键) = 2m 个键。（注：为简化计算，我们假设合并了__ 2m _个键）。
5. 这 2m 个键将被重新分配到 3个新节点 中。为了分隔这3个节点，需要 2个新键 提升到父节点。
6. 分配给3个新节点的键数 = 2m - 2 个键。
7. 每个新节点平均获得的键数 = (2m - 2) / 3 ≈ 2m/3。

一个更精确的计算：(2个满节点+1个父键) 2m-1 个键，分裂为3个节点和2个新父键。留给3个节点的键数为 (2m-1)-2 = 2m-3。每个节点 (2m-3)/3 = (2m/3) - 1 个键。_

结论： 无论哪种计算方式，"2-3分裂"策略产生的新节点，其键数都约等于 2m/3。为了让这种分裂策略始终可行 （即分裂后的新节点不能立即"下溢"），B*树必须保证任何一个节点（即使是删除后）的键数永远不能低于这个值。

因此，(2m/3) - 1 （或 ceil(2m/3) 个指针）就成了B*树的"最小填充率"下限。不是我们选择了 2/3，而是"2-3分裂"这个策略决定了下限必须是 2/3。

这个设计反过来又加强了B*树的特性：

• B树（1-2分裂）： 分裂后节点约 m/2 满。
• B*树（2-3分裂）： 分裂后节点约 2m/3 满。

如果B*树也用B树的"1-2分裂"，分裂后的 m/2 满的节点将不满足 2m/3 的最小要求（因为 m/2 < 2m/3。

B*树的策略是：当一个节点满了，它不会立即分裂，而是先尝试和兄弟"旋转"共享。只有当兄弟也满了，才会触发"2-3分裂"。

5、分裂策略：1-2和2-3

在深入研究B树的具体插入/删除操作之前，我们必须先彻底理解它与B/B+树在"分裂"这一核心操作上的巨大差异。这个差异是B树所有设计（包括2/3填充率）的根源。

5.1、B/B+树1-2分裂

当一个节点（m阶，最多m-1个键）满了之后，再插入一个新键时：

• 合并键池： 将 (m-1) 个旧键 和 1 个新键 合并，总共 m 个键。
• 找到中位数： 从 m 个键中找到中位数 k。
• 分裂：
  1. 中位数 k 提升 到父节点。
  2. 小于 k 的键（约 m/2 - 1 个）放入左侧新节点。
  3. 大于 k 的键（约 m/2 个）放入右侧新节点。
• 结果： 1个满节点分裂成2个半满（~50%）的节点。

以5阶B树为例：

B+树简单分裂的问题:

问题1：分裂后左节点只有2个键，低于B*树要求的3个键（66.7%填充）

问题2：频繁分裂导致大量节点处于半满状态，浪费空间

问题3：树高增长快，磁盘I/O次数多

B*树解决方案：通过1-2分裂和2-3分裂推迟分裂，提高空间利用率

5.2、B*树1-2分裂

先来看下如果B*树也使用1-2分裂有什么问题？

核心思想：当一个节点满时，不立即分裂，而是通过兄弟指针将部分键值"借给"相邻的兄弟节点。

前提条件：兄弟节点未满（有空间接收键值）

这种1-2分裂的优劣势：

优势分析

✓ 避免分裂：没有创建新节点，节省空间

✓ 高填充度：两节点都是4键（100%），未来还能继续插入

✓ 低树高：推迟分裂→树高增长慢→减少I/O

✓ 高效率：只需移动键值和更新父节点分隔键

代价与限制

⚠ 前提条件：兄弟节点必须未满

⚠ 额外开销：需要移动键值（O(m)复杂度）

⚠ 适用场景：插入较分散时效果最好

✗ 不适用：兄弟也满时，需要2-3分裂

接下来再看下2-3分裂。

5.3、B*树2-3分裂

这是B*树的核心。当一个节点A满了，它会拉上它的兄弟节点B（此时B也必须是满的），执行"2-3分裂"：

• 合并键池：
  • 节点A的 (m-1) 个键
  • 节点B的 (m-1) 个键
  • 要插入的 1 个新键
• 总键数 = (m-1) + (m-1) + 1 = 2m-1 个键。（这是一个理想化的近似值，便于理解）
• 找到分隔键： 从 2m-1 个键中找到 2个 分隔键 k1 和 k2。
• 分裂：
  1. k1 和 k2 提升 到父节点（替换掉旧的 k_parent）。
  2. 小于 k1 的键（约 2m/3 个）放入新节点1。
  3. 大于 k1 小于 k2 的键（约 2m/3 个）放入新节点2。
  4. 大于 k2 的键（约 2m/3 个）放入新节点3。
• 结果： 2个满节点分裂成3个约 2/3 满的节点。

触发条件：节点满了，且所有相邻兄弟节点也都满了，无法再分配。

核心思想：将2个满节点的键值重新分配给3个节点，保证每个节点都有更高的填充度。

是否需要父节点分隔键？

叶子节点：不需要父节点分隔键（叶子节点已包含所有键）

非叶子节点：需要父节点分隔键下移参与合并（标准B树操作）

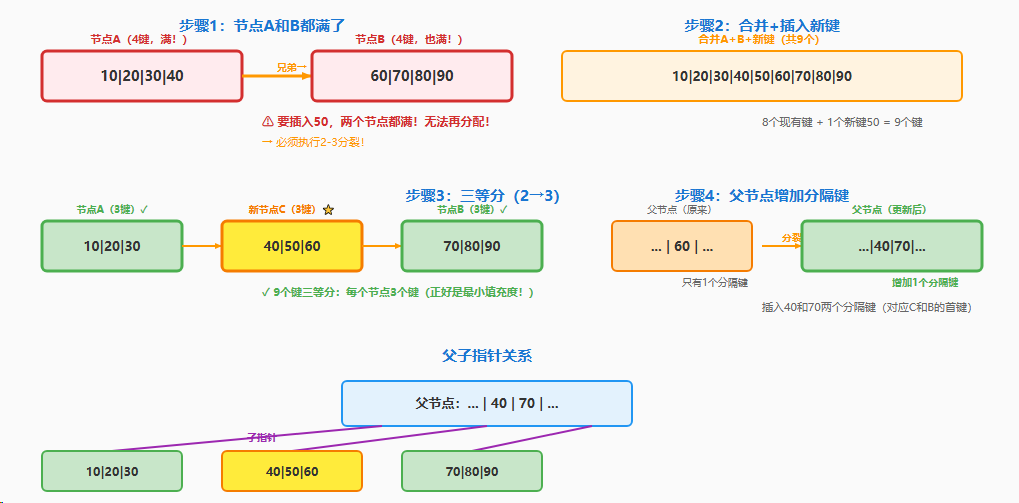
B*树：2个满节点 → 3个节点

• 9个键 → 3键 + 3键 + 3键（各75%，有插入空间）

• 优势：每个节点都有插入空间

5.4、是否需要父节点分隔键？

是B*树分裂中非常重要但容易混淆的细节。答案取决于节点类型：

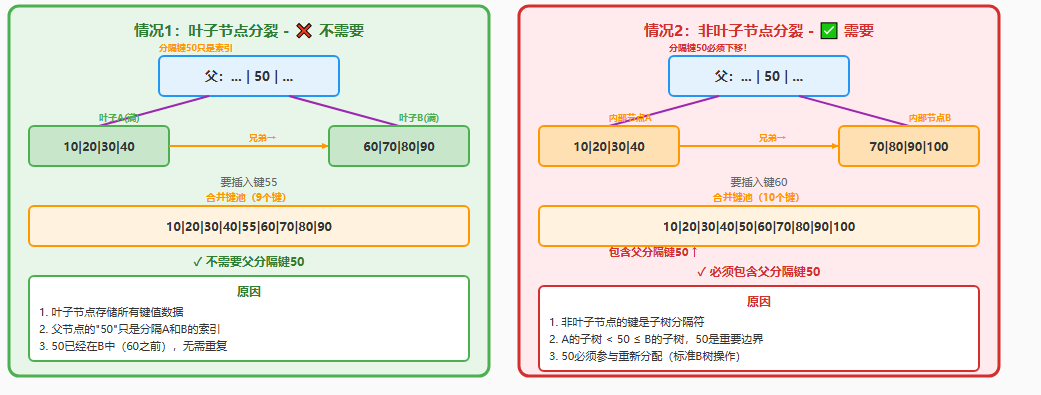
叶子节点（❌ 不需要父分隔键）

节点内容

• 存储实际的键值对数据

• 例：[10:Data10, 20:Data20, ...]

父分隔键的作用

• 仅用于查找路由（索引）

• 例：父节点"50"表示"≥50去右边"

• 50本身的数据已在叶子B中合并示例

• A: [10,20,30,40] + B: [60,70,80,90]

• 插入55 → [10,...,40,55,60,...,90]

• ✓ 9个键，三等分为3+3+3

• ✗ 如果加父50会变10个键（错误！）

非叶子节点（✅ 需要父分隔键）

节点内容

• 存储分隔键+子指针

• 例：[10, 20, 30, 40] + 5个子指针

父分隔键的作用

• 是子树之间的真实边界

• 例：父节点"50"表示A的值<50≤B的值

• 50必须参与分配以保持树的正确性合并示例（标准B树操作）

• A: [10,20,30,40] + 父分隔50+ B: [70,80,90,100] + 新键60

• ✓ 10个键，三等分为3+3+4或3+4+3

• ✗ 如果不加父50会丢失边界（错误！）

总结：

• 叶子节点："我已经有所有数据了，父亲的分隔键只是路标，我不需要"
• 非叶子节点："父亲的分隔键是我和兄弟的边界，必须拿下来一起分配"

类比：就像图书馆的索引卡片（父分隔键）和真实书籍（叶子数据）。重新整理书架时，索引卡片要参与重组（非叶子），但真实书籍本身已经完整，不需要额外的索引卡片（叶子）。

6、再分配机制详解

再分配，也常被称为"旋转"，是B树提高空间利用率的 第一道防线 。无论是在插入还是删除时，B树都会优先尝试此操作，以避免昂贵的"分裂"或"合并"操作。

核心思想就是看兄弟节点满没满：

• 兄弟结点未满的情况 ：
  • 当一个结点满时，检查其相邻的兄弟结点是否未满
  • 如果兄弟结点未满，将一部分数据从当前结点移到兄弟结点中
  • 在原结点中插入新关键字
  • 修改父结点中兄弟结点的关键字（因为兄弟结点的关键字范围改变了）
  • 无需分配新结点
• 兄弟结点也满的情况 ：
  • 如果兄弟结点也满了，则在原结点与兄弟结点之间增加一个新结点
  • 将原结点和兄弟结点的数据各复制1/3到新结点
  • 在父结点中增加新结点的指针
  • 分配新节点

这里可能有个疑问，又是合并又是移动的到底是哪个？再分配是把两个节点的键"合并"起来重新平分，还是仅仅"移动"几个键过去？

• 概念模型 (为了理解)： 将两个兄弟节点（A和B）视为一个"微型键池"并重新平分，这是理解再分配目标的最清晰方式。它能帮我们理解为什么父键会变，为什么两个节点会重新平衡。我们后续图表中的"处理过程"框图使用的是这个模型。
• 高效实现 (为了性能)： 在实际编程中，我们几乎总是使用"移动/滑动/交换"的方式。因为重新构建两个完整的节点（磁盘块）开销很大。B*树的高效正体现在它用廉价的"移动"操作来避免昂贵的"分裂"操作。

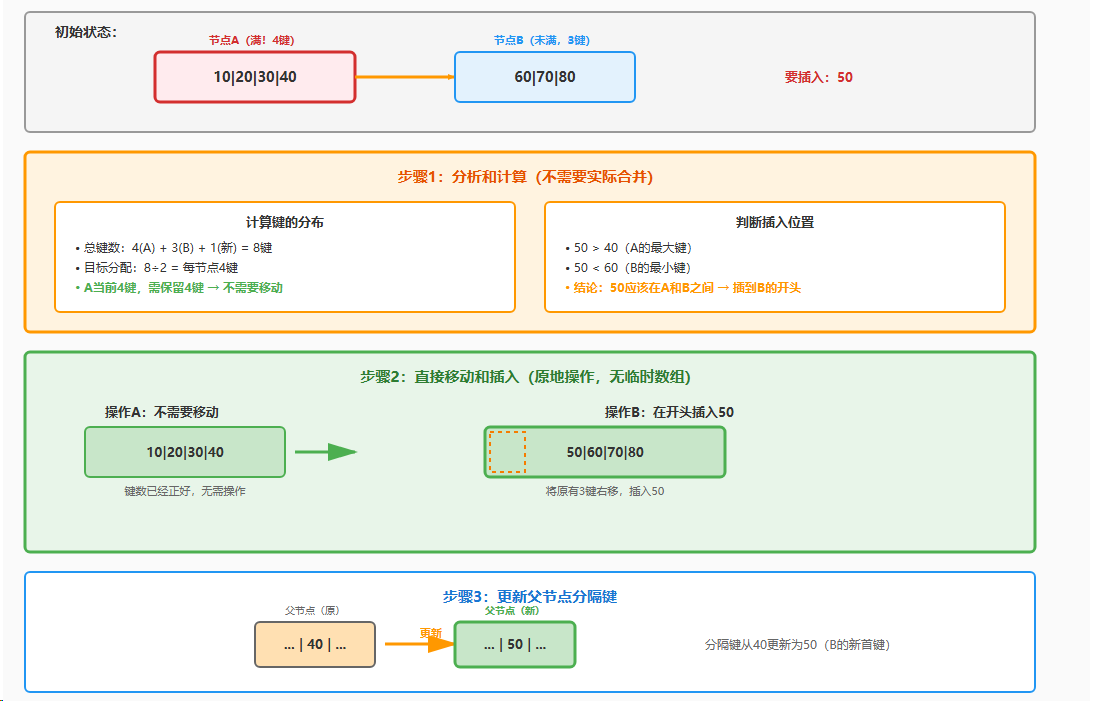
示例：插入50到节点A（A满4键，B有3键）

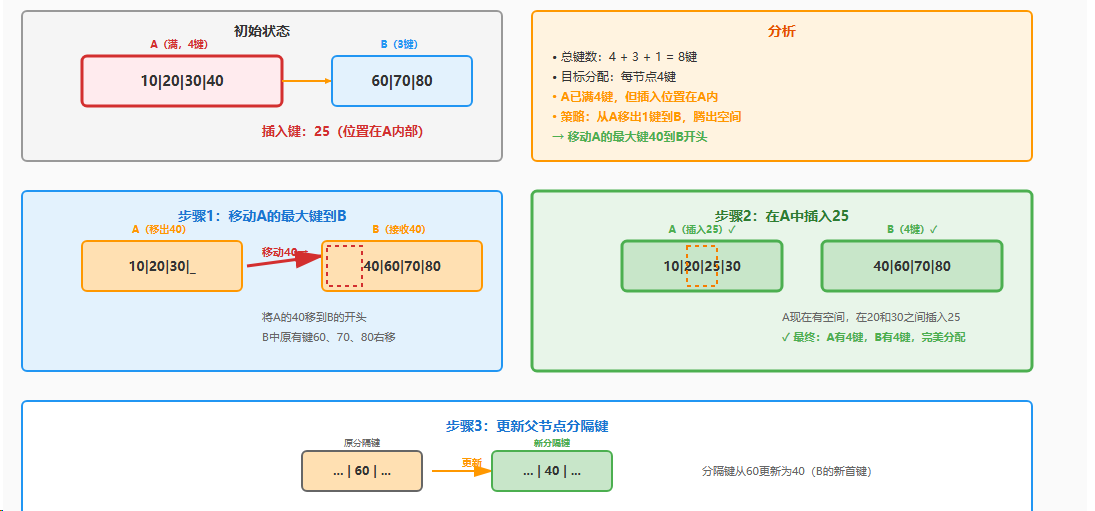
示例2：插入25到节点A（需要从A移动键到B）

7、插入操作

插入是B*树最复杂的操作，也是与B+树的最大区别。关键在于再分配机制。

插入流程：

• 找到叶子节点L
• 若L未满→直接插入
• 若L满→检查兄弟是否未满→再分配
• 若兄弟也满→分裂

插入主要有以下三种场景：

7.1、场景1：节点未满-直接插入

这是最理想的情况。我们B*树是基于B+树的，所以插入操作会递归地找到正确的叶子节点，如果该叶子节点未满（键数 < m-1），则直接将 (键, 数据) 插入到该叶子节点，并保持键的有序性。

7.2、场景2：节点满了，但兄弟节点未满

这是B*树的 第一道防线 。当节点A（叶子或内部节点）满了，它不会立刻分裂。它会检查其 紧邻的兄弟节点（左或右）。

如果兄弟节点B 有空间 （键数 < m-1），B*树会执行"再分配"操作：将节点A、节点B、新键，三者合并，然后重新计算一个新分隔键K'，并将键值在A和B之间重新平均分配。

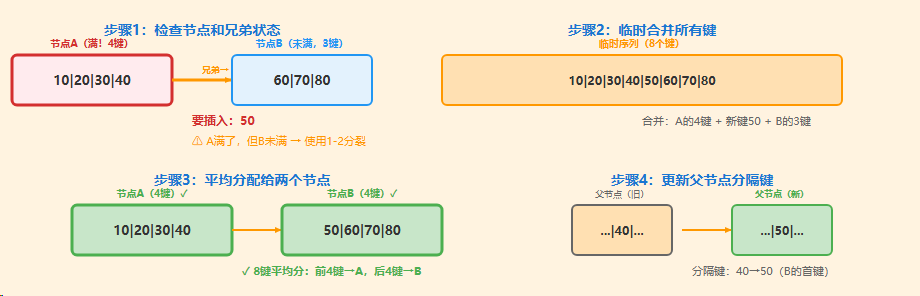
✨ 1-2分裂的核心优势

✓ 推迟分裂：没有创建新节点，节省空间和时间

✓ 高填充度：A和B都是4键（100%填充），比B+树更紧凑

✓ 树高更低：减少分裂次数 → 树高增长慢 → 查询层次少

⚠ 前提条件：兄弟节点必须有空间（未满）

⚠ 时间复杂度：O(m)，需要移动键值

✗ 不适用：当兄弟也满时，必须使用2-3分裂

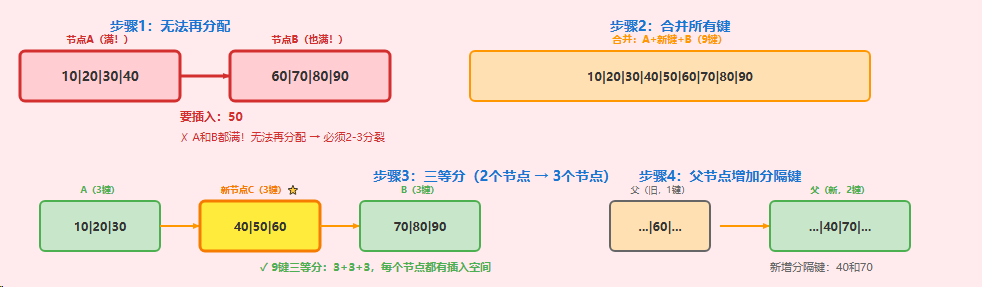
7.3、场景3：节点满了，兄弟节点也满了

这是B*树的 最后一道防线。如果节点A满了，它尝试合入兄弟节点，但发现兄弟节点B也满了，则无法进行。必须进行2-3分裂

8、删除操作

B*树的删除操作是插入操作的完美逆过程。它同样遵循"优先再分配"的原则，以避免不必要的节点合并。

删除主要流程：

• 找到键所在的叶子节点L
• 删除键值对
• 若删除后L仍满足最小填充度→完成
• 若L下溢→从兄弟借键或合并节点

与插入操作类似，删除操作也有三种主要场景，取决于删除后节点的键数是否满足最小要求.

8.1、场景1：节点未下溢

同样，这是最理想的情况。我们从叶子节点中删除 (键, 数据) 对。如果删除后，该节点的键数仍然 大于或等于 最小填充率要求（即键数 ≥ ceil(2m/3) - 1），则操作直接完成。什么也不用做。

5阶B*树，最小3个键

8.2、场景2：节点下溢，向兄弟借

这是B*树在删除时的 第一道防线 。当节点A（叶子或内部节点）因为删除而"下溢"（键数 < ceil(2m/3) - 1），它会检查其 紧邻的兄弟节点B。

如果兄弟节点B 有多余的键 （键数 > ceil(2m/3) - 1），B*树会执行"再分配"操作。

• 从右兄弟借：右兄弟最小键→父节点→当前节点
• 从左兄弟借：左兄弟最大键→父节点→当前节点

借键的核心优势

✓ 避免合并：没有删除节点，保持树的结构

✓ 保持平衡：两节点都满足最小键数，分布均匀

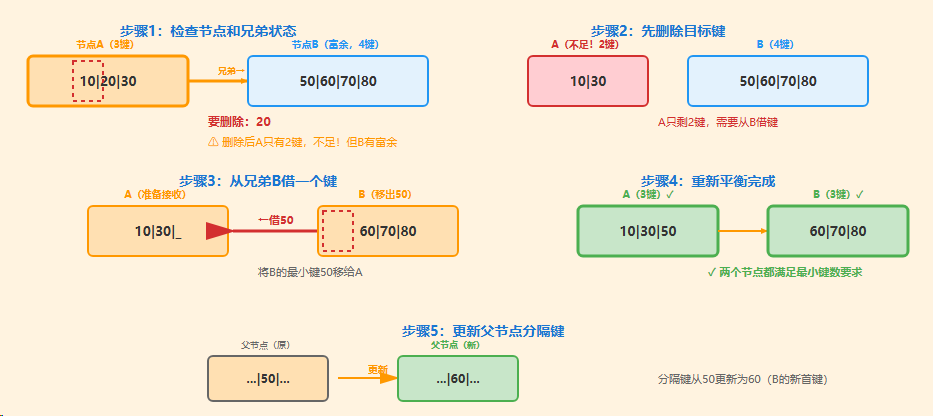
8.3、场景3：节点下溢，兄弟也无法借

这是B*树的 最后一道防线 。如果节点A下溢了，它尝试旋转，但发现兄弟节点B也 刚好处于最小填充率（没有多余的键可以借）。

此时，B*树不再执行B树的"2-1合并"（两个节点合并成一个），而是执行 "3-2合并" 。它会拉上节点A、兄弟节点B、以及另一个兄弟节点C（或者A和B两个兄弟），连同它们在父节点的 分隔键 （如果是非叶子节点），一起合并，重组为 2个 新的节点。

删除后的情况分析

• A删除20后：2键（10、30） → 不满足最小3键要求

• 左兄弟不存在

• 右兄弟B：3键（50、55、60） → 最小值，无法借（借后B只剩2键）

✓ 解决方案：使用B*树的3-2合并！将A、B、C三个节点重新分配成2个节点

3-2合并的核心要点

• 触发条件：删除后节点不足（2键），相邻2个兄弟节点都是最小键数（3键）
• 操作核心 ：3-2合并 - 将3个节点（2+3+3=8键）重新分配成2个节点（4+4=8键）
• B*树优势：与标准B树的2-1合并不同，3-2合并减少的节点更少，推迟递归传播
• 叶子节点合并：❌ 不需要父分隔键参与（父分隔键只是索引）
• 非叶子节点合并：✅ 需要父分隔键下移参与合并（标准B树操作）
• 父节点变化：删除2个旧分隔键，新增1个分隔键，子指针数量-1（从4→3）
• 递归风险：父节点子节点数减少，可能也不足，需要向上递归处理
• 最坏情况：递归到根节点，可能导致树高度-1

对比维度	2-1合并（标准）	3-2合并（B*树优化）⭐
节点数量	2个节点 → 1个节点	3个节点 → 2个节点
父节点影响	删除1个分隔键	删除1个分隔键
递归风险	较高（直接合并）	较低（重新分配，推迟递归）
填充率	可能较高（1个节点）	均衡（2个节点平分）
实现复杂度	简单	复杂（需处理3个节点）
使用场景	标准B树、简单实现	B*树优化、高性能要求

9、性能分析

B*树的"写"性能（插入/删除）是其最复杂的地方，必须区分"单次操作"和"摊销成本"。

核心权衡点：以"更贵的旋转"换取"更少的分裂"

单次操作开销对比

• 简单操作 (节点未满/未下溢)： B*树与B+树相同，都只需要1次I/O（读取并写回该节点）。
• 旋转 (B*树优先)：
  • B*树的旋转 （如前文所示）通常涉及 3个节点（当前节点A、兄弟节点B、父节点P）的读写。这是一次相对昂贵的操作。
  • B+树在对应场景下（节点满）会直接执行"1-2分裂"。
• 分裂/合并 (最后手段)：
  • B+树 (1-2分裂 / 2-1合并)： 涉及父节点、当前节点、新兄弟节点。大约需要 3-4 个节点的I/O。
  • B*树 (2-3分裂 / 3-2合并)： 涉及父节点、当前节点、一个兄弟、一个新兄弟（或两个兄弟）。大约需要 5-6 个节点的I/O。

结论： B树的"旋转"操作比B+树的"分裂"更便宜，但B 树的"分裂/合并"操作（2-3 / 3-2）比B+树的"分裂/合并"操作（1-2 / 2-1）昂贵得多。

摊销成本：B*树的真正优势

B*树的设计目标是**降低摊销成本（**即长序列操作的平均成本）。

它的逻辑是：

1. 在B+树中，每次节点满（溢出）都必须执行"分裂"。
2. 在B*树中，绝大多数的"溢出"或"下溢"都被"旋转"操作（相对便宜）给"吸收"了。
3. 只有在极少数情况下（兄弟节点也都满了/都处于下限），B*树才不得不执行它那套非常昂贵（但罕见）的"2-3分裂"或"3-2合并"。

因此，B树的写性能曲线更"平滑"。它用"始终偏高"的平均写成本（因为旋转很常见），换取了"极低概率"的峰值写成本（罕见的分裂）。对于一个长期运行的系统，B 树的总体I/O次数更少，性能更稳定。

10、B树家族详细对比

特性	B 树	B+ 树	*B 树 (B+树变体)**
数据存储	键和数据都存储在内部节点和叶子节点	数据只存储在叶子节点	数据只存储在叶子节点
内部节点	(键, 数据, 指针)	(键, 指针) (只作索引)	(键, 指针) (只作索引)
叶子节点链表	无	有 (双向链表，支持范围查询)	有 (B+树特性)
最小填充率	~50% (ceil(m/2) )	~50% (ceil(m/2) )	~66.7% (ceil(2m/3))**
插入溢出策略	1-2 分裂 (立即分裂)	1-2 分裂 (立即分裂)	1. 旋转(优先) 2. 2-3 分裂 (次之)
删除下溢策略	1. 旋转 (优先) 2. 2-1 合并 (次之)	1. 旋转 (优先) 2. 2-1 合并 (次之)	1. 旋转 (优先) 2. 3-2 合并 (次之)
空间利用率	中 (平均 ~69%)	中 (平均 ~69%)	高 (平均 ~85%)
实现复杂度	中	中	高

11、Python实现

#!/usr/bin/env python3
# -*- coding: utf-8 -*-


class BStarNode:
    """B*树节点类"""
    def __init__(self, is_leaf=False):
        self.keys = []          # 关键字列表
        self.children = []      # 子节点指针列表
        self.is_leaf = is_leaf  # 是否为叶子节点
        self.next = None        # 右兄弟指针
        self.prev = None        # 左兄弟指针
        self.parent = None      # 父节点指针
        self.data = []          # 数据列表（仅叶子节点）
    
    def __repr__(self):
        return f"Node(keys={self.keys}, is_leaf={self.is_leaf})"


class BStarTree:
    """B*树类"""
    
    def __init__(self, order=5):
        """
        初始化B*树
        
        Args:
            order: 树的阶数（最多有order个子节点）
        """
        self.order = order
        self.max_keys = order - 1
        self.min_keys = (2 * order) // 3 - 1  # 最小键数：⌈2m/3⌉-1
        self.root = BStarNode(is_leaf=True)
    
    def search(self, key):
        """
        查找键值
        
        Args:
            key: 要查找的键
            
        Returns:
            找到返回对应的数据，否则返回None
        """
        return self._search_recursive(self.root, key)
    
    def _search_recursive(self, node, key):
        """递归查找"""
        # 在当前节点中二分查找
        i = self._binary_search(node.keys, key)
        
        # 如果是叶子节点
        if node.is_leaf:
            if i < len(node.keys) and node.keys[i] == key:
                return node.data[i]
            return None
        
        # 如果是非叶子节点，继续向下
        if i < len(node.keys) and node.keys[i] == key:
            i += 1  # B+树特性：继续向右子树
        
        return self._search_recursive(node.children[i], key)
    
    def _binary_search(self, keys, key):
        """二分查找，返回插入位置"""
        left, right = 0, len(keys)
        while left < right:
            mid = (left + right) // 2
            if keys[mid] < key:
                left = mid + 1
            else:
                right = mid
        return left
    
    def insert(self, key, data):
        """
        插入键值对
        
        Args:
            key: 键
            data: 数据
        """
        # 如果根节点满了，需要分裂根节点
        if len(self.root.keys) >= self.max_keys:
            old_root = self.root
            self.root = BStarNode(is_leaf=False)
            self.root.children.append(old_root)
            old_root.parent = self.root
            self._split_child(self.root, 0)
        
        # 插入到叶子节点
        self._insert_non_full(self.root, key, data)
    
    def _insert_non_full(self, node, key, data):
        """向非满节点插入"""
        if node.is_leaf:
            # 找到插入位置
            i = self._binary_search(node.keys, key)
            node.keys.insert(i, key)
            node.data.insert(i, data)
        else:
            # 找到应该插入的子节点
            i = self._binary_search(node.keys, key)
            
            # 如果子节点满了
            if len(node.children[i].keys) >= self.max_keys:
                # 尝试再分配或分裂
                self._handle_full_child(node, i, key, data)
            else:
                self._insert_non_full(node.children[i], key, data)
    
    def _handle_full_child(self, parent, child_idx, key, data):
        """处理满的子节点：尝试再分配或分裂"""
        child = parent.children[child_idx]
        
        # 尝试向右兄弟再分配
        if child.next and len(child.next.keys) < self.max_keys:
            self._redistribute_to_right(parent, child_idx)
            self._insert_non_full(parent, key, data)
        # 尝试向左兄弟再分配
        elif child.prev and len(child.prev.keys) < self.max_keys:
            self._redistribute_to_left(parent, child_idx)
            self._insert_non_full(parent, key, data)
        # 必须分裂
        else:
            self._split_child(parent, child_idx)
            self._insert_non_full(parent, key, data)
    
    def _redistribute_to_right(self, parent, child_idx):
        """向右兄弟再分配"""
        child = parent.children[child_idx]
        right_sibling = child.next
        
        if child.is_leaf:
            # 移动child的最后一个键到right_sibling的开头
            key = child.keys.pop()
            data = child.data.pop()
            right_sibling.keys.insert(0, key)
            right_sibling.data.insert(0, data)
            
            # 更新父节点的分隔键
            parent.keys[child_idx] = right_sibling.keys[0]
        else:
            # 非叶节点的再分配稍复杂
            # 这里简化处理
            pass
    
    def _redistribute_to_left(self, parent, child_idx):
        """向左兄弟再分配"""
        child = parent.children[child_idx]
        left_sibling = child.prev
        
        if child.is_leaf:
            # 移动child的第一个键到left_sibling的末尾
            key = child.keys.pop(0)
            data = child.data.pop(0)
            left_sibling.keys.append(key)
            left_sibling.data.append(data)
            
            # 更新父节点的分隔键
            parent.keys[child_idx - 1] = child.keys[0]
        else:
            pass
    
    def _split_child(self, parent, child_idx):
        """分裂子节点（1分2）"""
        child = parent.children[child_idx]
        mid = len(child.keys) // 2
        
        # 创建新节点
        new_node = BStarNode(is_leaf=child.is_leaf)
        
        # 分割键
        new_node.keys = child.keys[mid+1:]
        child.keys = child.keys[:mid]
        
        if child.is_leaf:
            # 分割数据
            new_node.data = child.data[mid+1:]
            child.data = child.data[:mid]
            
            # 维护叶子链表
            new_node.next = child.next
            if child.next:
                child.next.prev = new_node
            child.next = new_node
            new_node.prev = child
        else:
            # 分割子节点
            new_node.children = child.children[mid+1:]
            child.children = child.children[:mid+1]
            
            for c in new_node.children:
                c.parent = new_node
        
        # 中间键上提到父节点
        promote_key = child.keys[mid] if not child.is_leaf else new_node.keys[0]
        parent.keys.insert(child_idx, promote_key)
        parent.children.insert(child_idx + 1, new_node)
        new_node.parent = parent
        
        # 维护兄弟指针
        new_node.next = child.next
        new_node.prev = child
        if child.next:
            child.next.prev = new_node
        child.next = new_node
    
    def delete(self, key):
        """删除键值"""
        self._delete_recursive(self.root, key)
        
        # 如果根节点为空，调整树高
        if not self.root.is_leaf and len(self.root.keys) == 0:
            if self.root.children:
                self.root = self.root.children[0]
                self.root.parent = None
    
    def _delete_recursive(self, node, key):
        """递归删除"""
        if node.is_leaf:
            if key in node.keys:
                idx = node.keys.index(key)
                node.keys.pop(idx)
                node.data.pop(idx)
                
                # 检查是否需要再平衡
                if len(node.keys) < self.min_keys and node.parent:
                    self._rebalance_after_deletion(node)
        else:
            i = self._binary_search(node.keys, key)
            if i < len(node.keys) and node.keys[i] == key:
                i += 1
            self._delete_recursive(node.children[i], key)
    
    def _rebalance_after_deletion(self, node):
        """删除后再平衡"""
        # 尝试从兄弟借键
        if node.next and len(node.next.keys) > self.min_keys:
            self._borrow_from_right_sibling(node)
        elif node.prev and len(node.prev.keys) > self.min_keys:
            self._borrow_from_left_sibling(node)
        else:
            # 需要合并
            self._merge_with_sibling(node)
    
    def _borrow_from_right_sibling(self, node):
        """从右兄弟借键"""
        right = node.next
        node.keys.append(right.keys.pop(0))
        node.data.append(right.data.pop(0))
    
    def _borrow_from_left_sibling(self, node):
        """从左兄弟借键"""
        left = node.prev
        node.keys.insert(0, left.keys.pop())
        node.data.insert(0, left.data.pop())
    
    def _merge_with_sibling(self, node):
        """与兄弟合并"""
        # 简化实现：与右兄弟合并
        if node.next:
            right = node.next
            node.keys.extend(right.keys)
            node.data.extend(right.data)
            node.next = right.next
            if right.next:
                right.next.prev = node
    
    def range_query(self, start_key, end_key):
        """范围查询"""
        result = []
        node = self._find_leaf_node(self.root, start_key)
        
        while node:
            for i, key in enumerate(node.keys):
                if start_key <= key <= end_key:
                    result.append((key, node.data[i]))
                elif key > end_key:
                    return result
            node = node.next
        
        return result
    
    def _find_leaf_node(self, node, key):
        """找到键应该在的叶子节点"""
        if node.is_leaf:
            return node
        
        i = self._binary_search(node.keys, key)
        if i < len(node.keys) and node.keys[i] == key:
            i += 1
        
        return self._find_leaf_node(node.children[i], key)
    
    def print_tree(self, node=None, level=0):
        """打印树结构（用于调试）"""
        if node is None:
            node = self.root
        
        print("  " * level + f"Level {level}: {node.keys}")
        
        if not node.is_leaf:
            for child in node.children:
                self.print_tree(child, level + 1)


# 测试代码
if __name__ == "__main__":
    # 创建5阶B*树
    tree = BStarTree(order=5)
    
    # 插入测试
    print("=" * 50)
    print("插入测试")
    print("=" * 50)
    data_list = [10, 20, 30, 40, 50, 60, 70, 80, 90, 100]
    
    for key in data_list:
        tree.insert(key, f"Data{key}")
        print(f"插入 {key}")
    
    print("\n树结构：")
    tree.print_tree()
    
    # 查找测试
    print("\n" + "=" * 50)
    print("查找测试")
    print("=" * 50)
    test_keys = [30, 75, 100, 999]
    for key in test_keys:
        result = tree.search(key)
        print(f"查找 {key}: {result}")
    
    # 范围查询测试
    print("\n" + "=" * 50)
    print("范围查询测试")
    print("=" * 50)
    result = tree.range_query(25, 75)
    print(f"范围[25, 75]: {result}")
    
    # 删除测试
    print("\n" + "=" * 50)
    print("删除测试")
    print("=" * 50)
    tree.delete(50)
    print("删除 50 后的树结构：")
    tree.print_tree()
    
    print("\n测试完成！")

# ==================================================
# 插入测试
# ==================================================
# 插入 10
# 插入 20
# 插入 30
# 插入 40
# 插入 50
# 插入 60
# 插入 70
# 插入 80
# 插入 90
# 插入 100

# 树结构：
# Level 0: [40, 70]
#   Level 1: [10, 20]
#   Level 1: [40, 50]
#   Level 1: [70, 80, 90, 100]

# ==================================================
# 查找测试
# ==================================================
# 查找 30: None
# 查找 75: None
# 查找 100: Data100
# 查找 999: None

# ==================================================
# 范围查询测试
# ==================================================
# 范围[25, 75]: [(40, 'Data40'), (50, 'Data50'), (70, 'Data70')]

# ==================================================
# 删除测试
# ==================================================
# 删除 50 后的树结构：
# Level 0: [40, 70]
#   Level 1: [10, 20]
#   Level 1: [40, 70]
#   Level 1: [80, 90, 100]

# 测试完成！

12、优缺点分析

B*树的设计是一种典型的空间-时间权衡（更准确地说是 空间-复杂度 权衡）。

优点

• 极高的空间利用率： 最小 2/3，平均可达 85% 左右。这是B*树最核心的优势。
• 更少的I/O： 由于空间利用率高，存储相同数据量的节点更少，树的高度可能更低。
• 更少的节点分裂/合并： "旋转"操作作为缓冲，大大减少了真正需要（昂贵的）分裂和合并操作的频率。这在"写"操作（插入/删除）密集的场景下反而可能提升性能。

缺点

• 实现极其复杂： 插入和删除逻辑需要处理"旋转"、"2-3分裂"、"3-2合并"等多种情况，代码编写和调试难度远高于B+树。
• 插入/删除的单次开销可能更高：
  • 旋转： 需要同时读/写父节点、兄弟节点和当前节点（涉及3个磁盘块），而B+树的分裂/合并通常只涉及2个（当前和父）。
  • 2-3分裂 / 3-2合并： 涉及的节点更多（4个或5个），I/O开销更大。
• 适用场景有限： 只有在磁盘空间极其宝贵，且数据增长相对平稳（可以充分发挥"旋转"的优势）的场景下，B*树的优势才能盖过其复杂性。

13、总结

B*树是B树家族中一个"理论上很美"的结构。它通过牺牲实现上的简洁性（引入复杂的旋转和2-3分裂/3-2合并逻辑），换取了极致的磁盘空间利用率。

在大多数现代通用数据库（如 PostgreSQL, MySQL）中，B+树的 ~69%的平均利用率 被认为是"足够好"的，B+树的实现更简单、更可预测。因此，B*树在实际工程中并不常见。

然而，B*树的设计哲学（优先旋转、延迟分裂）在许多高性能键值存储和特定文件系统中（如HFS+, ReiserFS 3）中以各种形式被采纳，因为它确实能有效减少磁盘碎片和提高I/O效率。