本文是在看了 3Blue1Brown-深度学习之人工神经网络 视频后的学习笔记。3B1B的"深度学习"系列视频 用可视化动画和深入浅出的讲解让我们看清人工神经网络的本质。
我之前困惑 一个有大量参数组成的人工神经网络,是怎么训练学会识别出动植物,生成图像的。"梯度下降法"是人工神经网络"学会"知识的底层逻辑,机器通过梯度下降持续优化自身参数。
主体使用AI 生成
1、神经网络的学习目标
神经网络的"学习",本质上是在找一组最优的"权重和偏置"参数。3B1B在视频中以手写数字识别为例,形象地拆解了这个问题:
- 输入层是28×28像素的手写数字图像(784个神经元),隐藏层设两层(每层16个神经元),输出层是10个神经元(对应0-9十个数字)。
- 整个网络的参数的包括13000多个权重(连接神经元的"强弱系数")和偏置(神经元"激活门槛")。
- 在初始状态,这些参数都是随机初始化的,此时的神经网络是"瞎猜"的。类似像一个毫无经验的新手完全没有经验,只能凭直觉尝试。
那么目标已经清楚,后续需要做的就是通过训练数据,调整参数,找到最优参数,让识别准确率越来越高。
新的问题来了,怎么知道识别的准不准呢?此时需要一个"裁判"来判定差距有多少,这个裁判就是引入一个损失函数(Loss Function),它表示当前模型的预测值与真实值之间的差距。代价函数的输出值越小,说明模型预测越准确,参数越优;反之,代价越大,说明模型的错误越严重。
举个例子 :
假设输入"3"的图像,准确的输出应该是[0,0,0,1,0,0,0,0,0,0],若模型输出是[0.2,0.1,0.3,0.1,0.05,0.05,0.1,0.02,0.03,0.05],此时代价函数会计算两者每个元素的差值平方和,得到一个较大的数值,明确告诉网络"当前参数很差,需要调整"。
神经网络无法直接"看到"预测错误,只能通过损失函数的数值,感知自己的"表现好坏"。
2、梯度下降
在面对这么大量的参数,如何找到最优解?
在3Blue1Brown的视频用了一个非常形象的比喻:
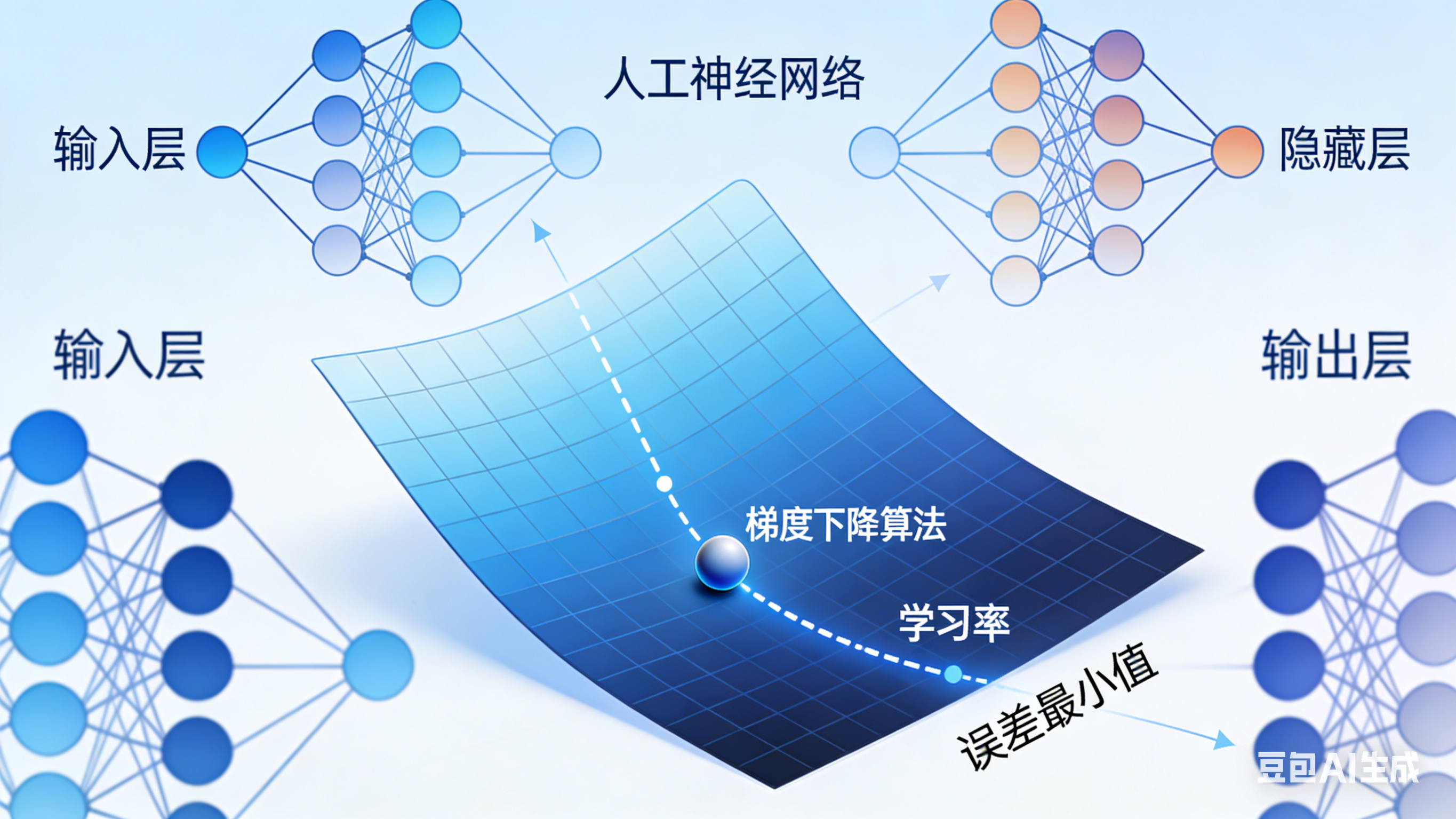
在一个复杂的地形中寻找最低点------你站在某座山的半山腰,看不见全局地图,只能根据脚下的坡度判断往哪里走才能最快地下山。这个"下山"的过程,就是梯度下降。
我们可以把损失函数的曲面想象成一座崎岖的山谷:山谷的每一个点,对应一组网络参数;山谷的最低点,就是代价最小的"最优参数点"(网络预测最准的状态);网络当前的参数状态,就是你在山谷中的位置。而你被困在浓雾中,只能看清脚下的区域,无法预判全局地形------这就像神经网络无法一次性找到最优参数,只能基于当前状态逐步调整。
在这种情况下,最快走到谷底(找到最优参数)的方法,就是梯度下降法的核心逻辑:在当前位置,找到坡度最陡的下坡方向,迈出一小步,重复这个过程,直到走到谷底。
神经网络的参数调整,这个过程拆解为3个关键步骤:
-
1.找方向:负梯度="最陡下坡方向
梯度(Gradient)是一个向量,3Blue1Brown的核心解读是:梯度指向"损失函数值增长最快的方向"(也就是山谷中最陡的上坡方向);梯度的反方向(负梯度)就是"损失函数值下降最快的方向"(最陡的下坡方向)。
-
2.定步长:学习率="迈步的大小"
找到下坡方向,还需要确定"迈多大一步",它直接决定了网络的"学习效率"和"学习效果"。
学习率太小:每次只迈一小步,下山速度极慢------对应神经网络,就是参数调整幅度太小,需要迭代成千上万次;
学习率太大:每次迈一大步,可能会跨过谷底,甚至跳到对面的山坡上。对应神经网络,就是参数调整幅度过大,导致损失函数值来回震荡,训练发散,无法收敛,模型越学越差。
-
3.做调整:迭代更新参数
明确了方向和步长,进行参数调整。这个过程是迭代进行的,循环往复,直到损失函数的值不再明显下降。