二叉树（下）

,二叉树算法题

1.单值二叉树

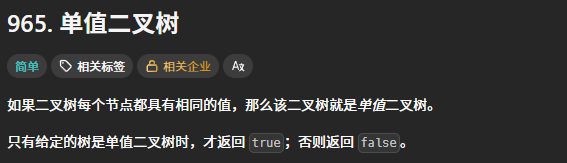
代码：

bool isUnivalTree(struct TreeNode* root) {
    if(root == NULL)
    {
        return true;
    }
    if(root->left&&root->val!=root->left->val)
    {
        return false;
    }
    if(root->right&&root->val!=root->right->val)
    {
        return false;
    }
    return isUnivalTree(root->left)&&isUnivalTree(root->right);
}

原理图：

二叉树的左右子树里的值如果相同，返回true，则返回false

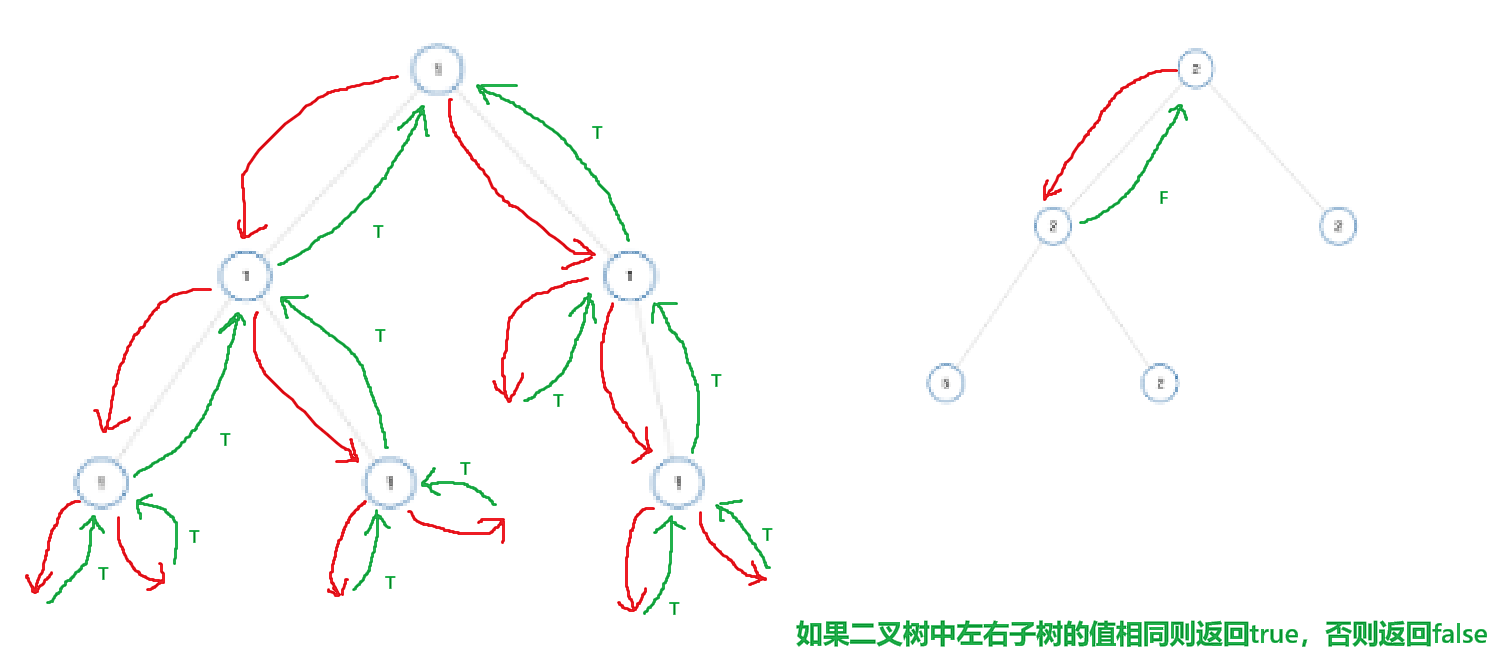
运行结果：

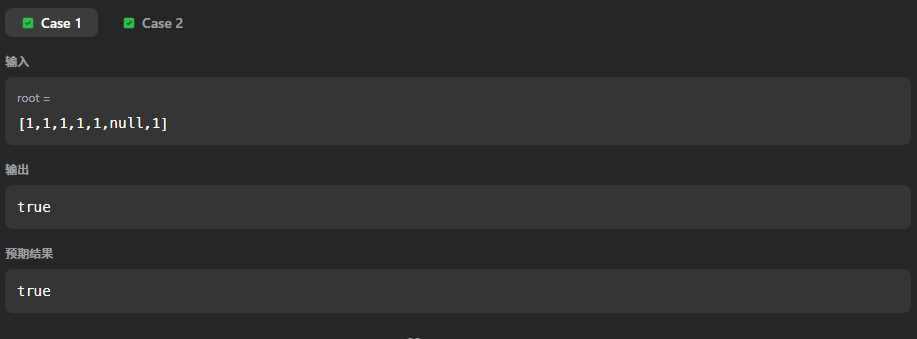
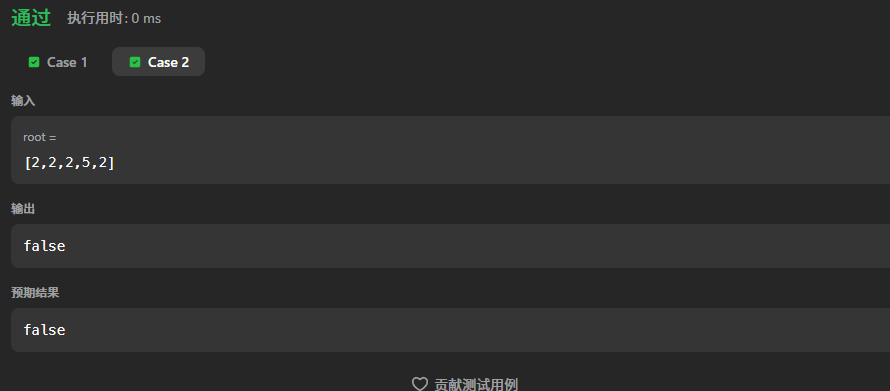
提交结果：

2.相同的树

代码：

bool isSameTree(struct TreeNode* p, struct TreeNode* q) {
    if(p == NULL&&q == NULL)
    {
        return true;
    }
    if(p == NULL || q == NULL)
    {
        return false;
    }
    if(p->val != q->val)
    {
        return false;
    }
    return isSameTree(p->left,q->left)&& isSameTree(p->right,q->right);
}

原理图：

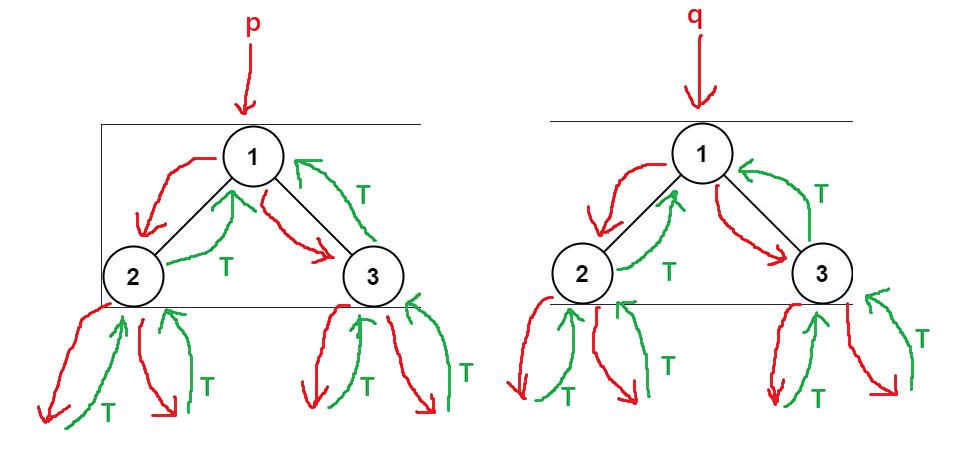
如果两个二叉树结构和数值相同返回true，否则返回flase

true:

flase:

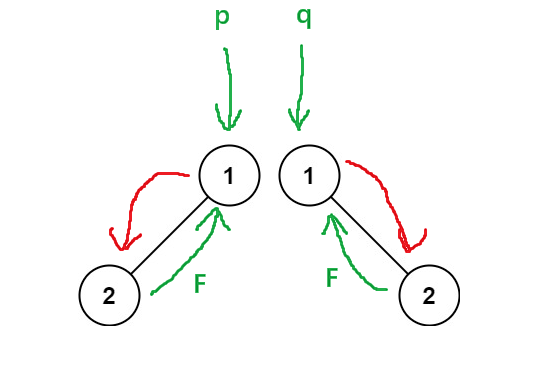
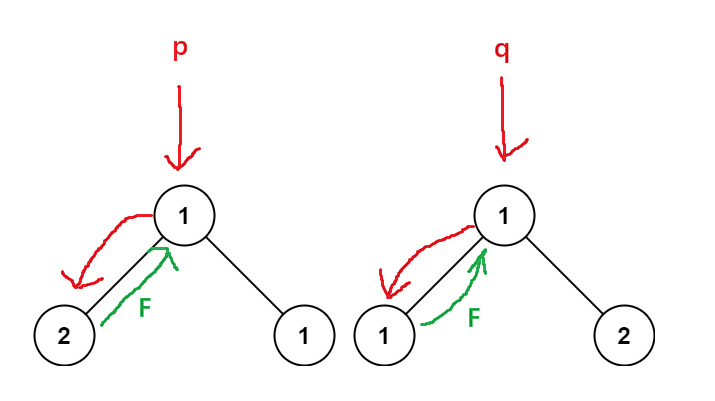
运行结果：

提交结果：

3.对称二叉树

代码：

bool isSameTree(struct TreeNode* p, struct TreeNode* q) {
    if(p == NULL&&q == NULL)
    {
        return true;
    }
    if(p == NULL || q == NULL)
    {
        return false;
    }
    if(p->val != q->val)
    {
        return false;
    }
    return isSameTree(p->left,q->right) && isSameTree(p->right,q->left);
}
bool isSymmetric(struct TreeNode* root) {
    return isSameTree(root->left,root->right);
}

原理：

检查左右子树是否对称，对称返回true，不对称则返回false

运行结果：

提交结果：

4.另一棵树的子树

代码：

bool isSameTree(struct TreeNode* p, struct TreeNode* q) {
    if(p == NULL&&q == NULL)
    {
        return true;
    }
    if(p == NULL || q == NULL)
    {
        return false;
    }
    if(p->val != q->val)
    {
        return false;
    }
    return isSameTree(p->left,q->left)&& isSameTree(p->right,q->right);
}
bool isSubtree(struct TreeNode* root, struct TreeNode* subRoot) {
    if(root == NULL)
    {
        return false;
    }
 if(isSameTree(root,subRoot))
 {
    return true;
 }   
 return isSubtree(root->left,subRoot) || isSubtree(root->right,subRoot);
}

原理图：

检查二叉树有没有相同的子树，如果有返回true，没有返回false

true：

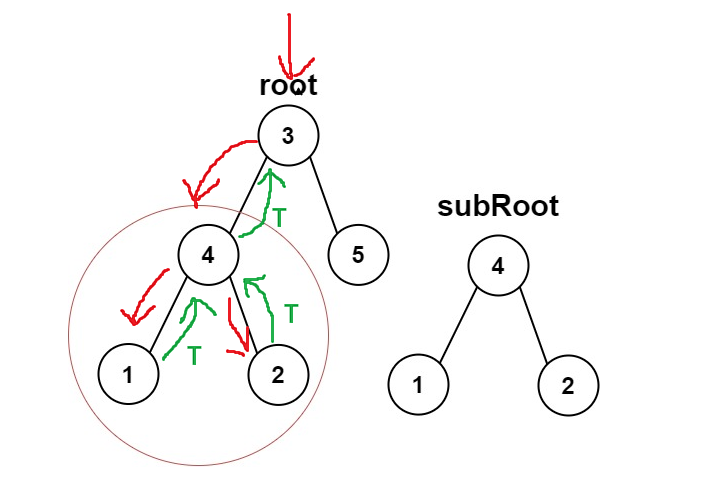
false：

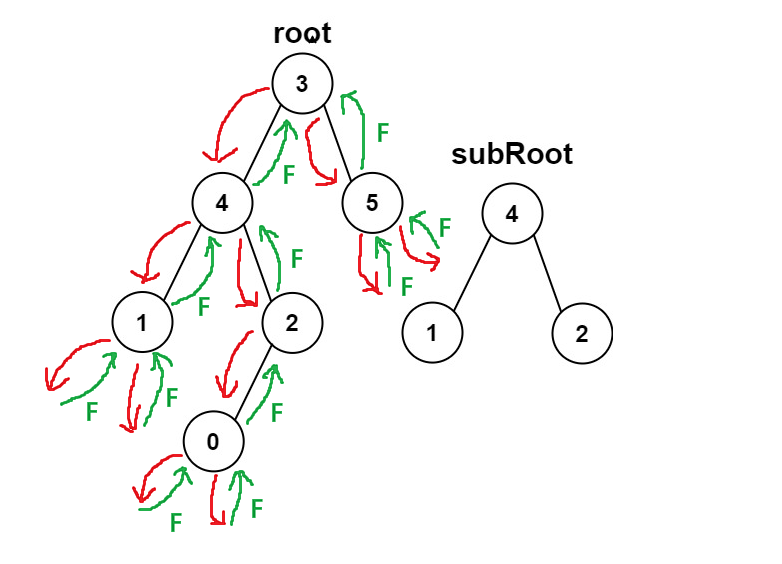
运行结果：

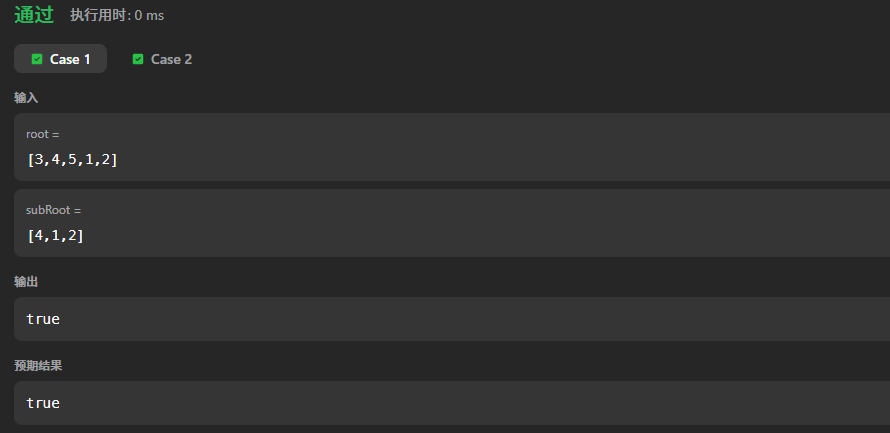
提交结果：

5.前序遍历

代码：

typedef struct TreeNode TreeNode;
int treeSize(TreeNode*root)
{
    if(root == NULL)
    {
        return 0;
    }
    return 1 + treeSize(root->left) + treeSize(root->right);
}
void prtorder(TreeNode*root,int*arr,int* pi)
{
    if(root == NULL)
    {
        return;
    }
    arr[(*pi)++] = root->val;
    prtorder(root->left,arr,pi);
    prtorder(root->right,arr,pi);
}

int* preorderTraversal(struct TreeNode* root, int* returnSize) {
    *returnSize = treeSize(root);
    int* arr = (int*)malloc(sizeof(int)*(*returnSize));
    int i = 0;
    prtorder(root,arr,&i);
    return arr;
}

原理：

先找出二叉树中有多少个节点，申请完内存空间后再进行前序遍历

运行结果：

提交结果：

6.中序遍历

代码：

typedef struct TreeNode TreeNode;
int treeSize(TreeNode* root)
{
    if(root == NULL)
    {
        return 0;
    }
    return 1 + treeSize(root->left) + treeSize(root->right);
}

void inorder(TreeNode* root,int *arr,int *pi)
{
    if(root == NULL)
    {
        return;
    }
    inorder(root->left,arr,pi);
    arr[(*pi)++] = root->val;
    inorder(root->right,arr,pi);
}


int* inorderTraversal(struct TreeNode* root, int* returnSize) {
    *returnSize = treeSize(root);
    int *arr = (int*)malloc(sizeof(int)*(*returnSize));
    int i = 0;
    inorder(root,arr,&i);
    return arr;
}

原理：

先找出二叉树中有多少个节点，申请完内存空间后再进行中序遍历

运行结果：

提交结果：

7.后续遍历

代码：

typedef struct TreeNode TreeNode;
int treeSize(TreeNode*root)
{
    if(root == NULL)
    {
        return 0;
    }
    return 1 + treeSize(root->left) + treeSize(root->right);
}
void postorder(TreeNode*root,int *arr, int *pi)
{
    if(root == NULL)
    {
        return;
    }
    postorder(root->left,arr,pi);
    postorder(root->right,arr,pi);
    arr[(*pi)++] = root->val;
}
int* postorderTraversal(struct TreeNode* root, int* returnSize) {
    *returnSize = treeSize(root);
    int* arr = (int*)malloc(sizeof(int)*(*returnSize));
    int i = 0;
    postorder(root,arr,&i);
    return arr;
}

运行结果：

8.二叉树的构建及遍历

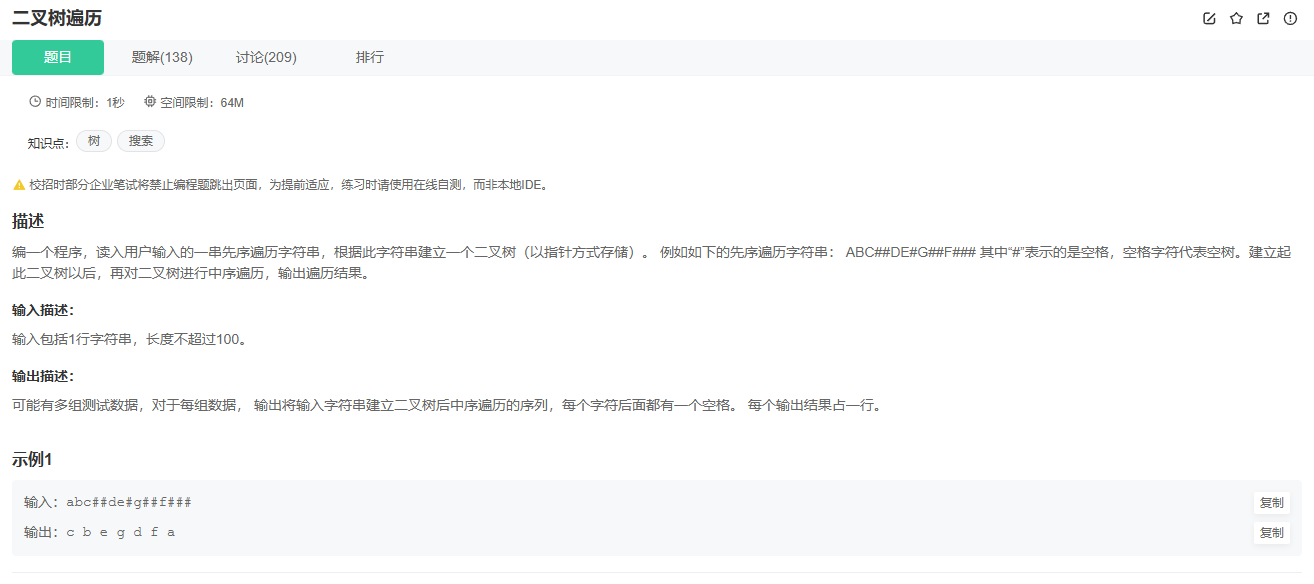
代码：

#include <stdio.h>
#include <stdlib.h>

typedef struct treenode{
    char data;
    struct treenode* left;
    struct treenode* right;
}treenode;

treenode* buynode(char ch)
{
    treenode* node = (treenode*)malloc(sizeof(treenode));
    if(node == NULL)
    {
        exit(1);
    }
    node->data = ch;
    node->left = node->right = NULL;
    return node;
}

treenode* createtree(char *arr,int *pi)
{
    if(arr[*pi] == '#')
    {
        (*pi)++;
        return NULL;
    }
    treenode *root = buynode(arr[*pi]);
    (*pi)++;
    root->left = createtree(arr, pi);
    root->right = createtree(arr, pi);

    return root;
}
void inorder(treenode* root)
{
    if(root == NULL)
    {
        return;
    }
    inorder(root->left);
    printf("%c ",root->data);
    inorder(root->right);
}
int main() {
   char arr[100];
   scanf("%s",arr);

   int i = 0;
   treenode*root = createtree(arr, &i);
   inorder(root);
   return 0;
}

运行结果：

提交结果：

二叉树选择题

二叉树性质：

对任何一棵二叉树, 如果度为 0 其叶结点个数为n0 , 度为 2 的分支结点个数为n2 ,则有 n0 = n2 + 1

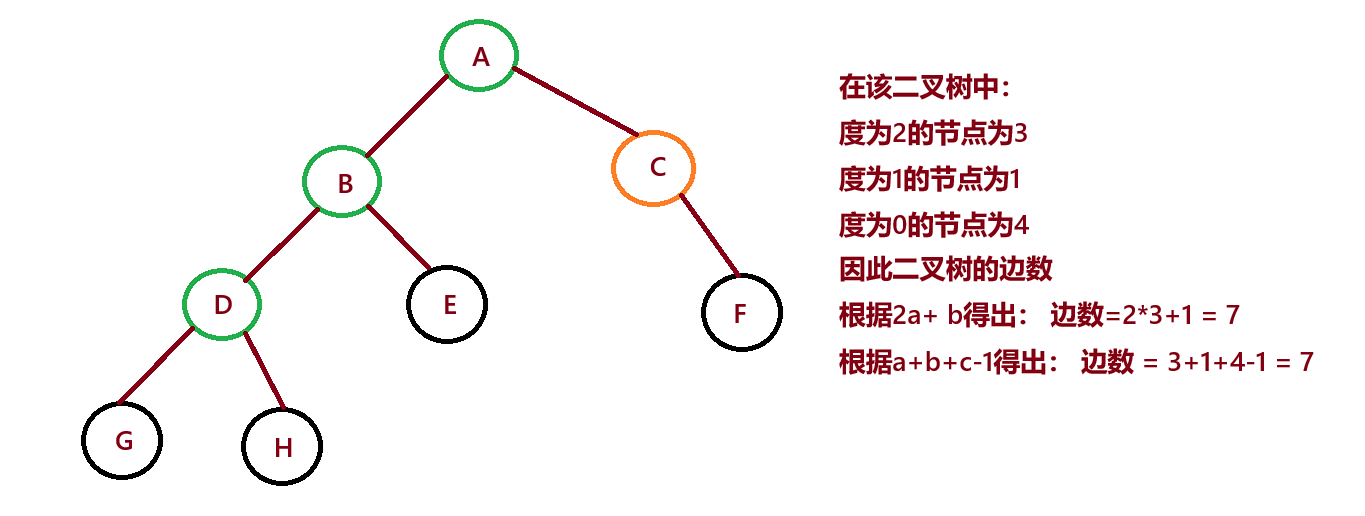
证明上述性质：

假设一个二叉树有 a 个度为2的节点， b 个度为1的节点， c 个叶节点，则这个二叉树的边数是 2a+b

另一方面，由于共有 a+b+c 个节点，所以边数等于 a+b+c-1

结合上面两个公式：

2a+b = a+b+c-1 ，即： a = c-1

根据二叉树的性质，完成以下选择题：

1. 某二叉树共有 399 个结点，其中有 199 个度为 2 的结点，则该二叉树中的叶子结点数为

A 不存在这样的二叉树

B 200

C 198

D 199

我们先来分析题目

已知二叉树有399个节点，其中度为2的节点有199个，根据二叉树的特性为n0= n2 + 1

n2 = 199

n0 = 199+1 = 200

答案是B

2.在具有 2n 个结点的完全二叉树中，叶子结点个数为

A n

B n+1

C n-1

D n/2

题目分析：

在完全二叉树中2n = n0+n1+n2，我们知道n2 = n0 - 1因此可以写成，2n = n0+n1+n0 - 1简化后得到2n = 2n0 + n1- 1 在一颗完全二叉树中n1 不是0 就是1，将两个数都算一遍

n1 = 0；2n0 - 1 = 2n ---> n0 = n + 1/2

n1 = 1；2n0 = 2n ---> n0 = n

答案是A

3.一棵完全二叉树的结点数位为531个，那么这棵树的高度为

A 11

B 10

C 8

D 12

题目分析：

一个满二叉树为 2^h-1;h = log(n+1)

完全二叉树为 2^h - 1 >= n

因此完全二叉树为：2^h - 1 >= 531

2^10 - 1 = 1023

1023 > 531

答案是B

4.一个具有767个结点的完全二叉树，其叶子结点个数为

A 383

B 384

C 385

D 386

题目分析：

根据二叉树的性质可以得到 n0+n1+n2 = 767

n2 = n0 - 1

可以写成：n0+n1+n0-1 = 767,简化后得到2n0 + 1 - 1 = 767

完全二叉树中n1 不是0 就是1

n1 = 0； 2n0 + 0 - 1 = 767---> 2n0 - 1 = 767 --->2n0 = 768 ---->768/2 = 384

n1 = 1； 2n0+1-1 = 767 --->2n0 = 767 --->767/2 = 383.5

答案是B

链式二叉树遍历选择题

1.某完全二叉树按层次输出（同一层从左到右）的序列为 ABCDEFGH 。该完全二叉树的前序序列为

A ABDHECFG

B ABCDEFGH

C HDBEAFCG

D HDEBFGCA

题目分析：

前序序列的排序方式为根左右，所以为ABDHECFG

答案是A

2.二叉树的先序遍历和中序遍历如下：先序遍历：EFHIGJK;中序遍历：HFIEJKG.则二叉树根结点为

A E

B F

C G

D H

题目分析：

先序遍历的遍历方式为根左右，E在先序遍历的第一位

答案是A

3.设一课二叉树的中序遍历序列：badce，后序遍历序列：bdeca，则二叉树前序遍历序列为____

A adbce

B decab

C debac

D abcde

题目分析：

我们先将中序遍历和后序遍历先提取出来

开始排序，在后续遍历时最后一个为根节点，先将a提取出来

之后剩下bdce,后续遍历是bdec，b为左子树cde为右子树，所以先将b放到左子树

之后看中序遍历，中序遍历遍历顺序为左根右，因此可以得到

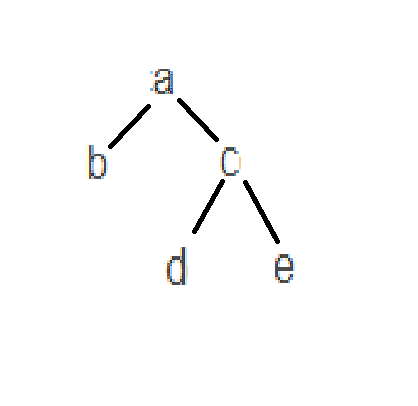
答案为D

4.某二叉树的后序遍历序列与中序遍历序列相同，均为 ABCDEF ，则按层次输出（同一层从左到右） 的序列

A FEDCBA

B CBAFED

C DEFCBA

D ABCDEF

答案分析：

这里说中序遍历和后续遍历都为ABCDEF，我们知道后续遍历的遍历顺序为左右根，根在最后一个

我们看到F在最后一个，而只有A选项F在第一个

答案为A