一 真题2010-8
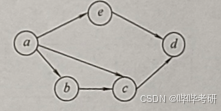
2010-08. 对右图进行拓扑排序,可以得到不同拓扑序列的个数是( )。
A. 4
B. 3
C. 2
D. 1
二 题目要素解析
核心概念 :拓扑排序
- 对有向无环图(DAG)的顶点进行排序,使得对于任意一条有向边 (u,v),顶点 u 都排在 v 的前面。
- 一个 DAG 可能有多个合法的拓扑序列。
解题步骤:
- 找出所有入度为 0 的顶点作为起点。
- 每次选择一个入度为 0 的顶点输出,并删除该顶点及其所有出边。
- 重复步骤 2,直到所有顶点都被输出。
图中顶点与边:
- 顶点:a,b,c,d,e
- 边:a→e, a→b, a→c, b→c, e→d, c→d
三 哔哔详解
步骤 1:确定起点
图中入度为 0 的顶点只有 a,所以拓扑序列的第一个元素必然是 a。
输出:[a]
删除 a 及其出边后,顶点 b,c,e 的入度减 1,此时入度为 0 的顶点为 b, e。
步骤 2:选择第二个顶点
有两种选择:b 或 e。
分支 1:选择 e 作为第二个顶点
输出:[a, e]
删除 e 及其出边后,顶点 d 的入度减 1。此时入度为 0 的顶点为 b。
输出:[a, e, b]
删除 b 及其出边后,顶点 c 的入度减 1。此时入度为 0 的顶点为 c。
输出:[a, e, b, c]
删除 c 及其出边后,顶点 d 的入度减 1。此时入度为 0 的顶点为 d。
输出:[a, e, b, c, d]
得到序列:a e b c d
分支 2:选择 b 作为第二个顶点
输出:[a, b]
删除 b 及其出边后,顶点 c 的入度减 1。此时入度为 0 的顶点为 e, c。
子分支 2.1:选择 e 作为第三个顶点
输出:[a, b, e]
删除 e 及其出边后,顶点 d 的入度减 1。此时入度为 0 的顶点为 c。
输出:[a, b, e, c, d]
得到序列:a b e c d
子分支 2.2:选择 c 作为第三个顶点
输出:[a, b, c]
删除 c 及其出边后,顶点 d 的入度减 1。此时入度为 0 的顶点为 e。
输出:[a, b, c, e, d]
得到序列:a b c e d
步骤 3:统计序列个数
我们得到了 3 个不同的拓扑序列:
a e b c da b e c da b c e d
四 参考答案
B ✅
五 考点精析
5.1 拓扑排序概念
一、 概念定义
1. 有向无环图 (DAG)
- 定义:一个有向图中不存在环,则称为有向无环图。
- 应用场景:表示工程的施工流程、课程的先修关系、软件的模块依赖等。
2. 拓扑排序
- 定义:对 DAG 的顶点进行排序,使得对于图中的任意一条有向边 (u,v),顶点 u 在序列中都出现在顶点 v 的前面。
- 结果 :得到的序列称为拓扑序列。
- 注意 :拓扑序列不一定唯一。
二、 性质特征
-
存在性:
- 只有 DAG(有向无环图) 才有拓扑序列。
- 如果图中有环,则无法进行拓扑排序(因为环上的节点互相依赖,谁也不能排在谁前面)。
-
序列不唯一性:
- 如果在排序过程中,某一步有多个入度为 0 的顶点可选,则不同的选择顺序会产生不同的拓扑序列。
-
入度与出度:
- 拓扑排序的过程本质上是不断 "消除" 入度为 0 的节点及其影响的过程。
5.2 关键路径与拓扑排序的结合
1. 核心概念
- 事件:顶点(代表某个阶段的完成)。
- 活动:边(代表具体的工作)。
- 最早发生时间 (ve):从源点到该顶点的最长路径长度(事件最早什么时候能开始)。
- 最迟发生时间 (vl):在不推迟整个工程完成时间的前提下,事件最迟必须发生的时间。
- 关键活动 :e=le=le=l 的活动(eee 是活动最早开始时间,lll 是活动最迟开始时间)。关键活动组成的路径即为关键路径。
2. 计算步骤(必须结合拓扑排序)
第一步:求 ve (最早时间) ------ 顺推(拓扑序)
- 初始化:源点 ve[start]=0ve[start]=0ve[start]=0。
- 按照拓扑序列顺序遍历:
- 对于边 (u→v),ve[v]=max(ve[v],ve[u]+len(u,v))(u→v),ve[v]=max(ve[v],ve[u]+len(u,v))(u→v),ve[v]=max(ve[v],ve[u]+len(u,v))。
- 含义 :只有 uuu 做完了,vvv 才能开始,取最长的那个路径作为瓶颈。
第二步:求 vl (最迟时间) ------ 逆推(逆拓扑序)
-
初始化:汇点 vl[end]=ve[end]vl[end]=ve[end]vl[end]=ve[end]。
-
按照
逆拓扑序列
顺序遍历:
- 对于边 (u→v),vl[u]=min(vl[u],vl[v]−len(u,v))(u→v),vl[u]=min(vl[u],vl[v]−len(u,v))(u→v),vl[u]=min(vl[u],vl[v]−len(u,v))。
- 含义 :vvv 最迟要开始,uuu 必须提前做完,留出活动时间。
第三步:求活动的 e 和 l
- 活动 aia_iai 对应边 (u→v):
- e(i)=ve[u]e(i)=ve[u]e(i)=ve[u] (活动最早开始时间 = 起点事件最早时间)。
- l(i)=vl[v]−len(u,v)l(i)=vl[v]−len(u,v)l(i)=vl[v]−len(u,v) (活动最迟开始时间 = 终点事件最迟时间 - 活动耗时)。
- 若 e(i)==l(i)e(i)==l(i)e(i)==l(i),则该活动为关键活动。
5.3 拓扑排序算法实现
5.3.1 kahn 算法
5.3.1.1 kahn算法提纲
- 思想:不断删除入度为 0 的节点
- 步骤:
- 计算所有顶点入度
- 将入度为 0 的顶点入队
- 出队一个顶点,加入结果
- 更新其邻接点入度,若变为 0 则入队
- 重复直到队空
- 判断环:若结果长度 < 总顶点数 → 有环
5.3.1.2 C 语言实现(Kahn 算法)
c
#include <stdio.h>
#include <stdlib.h>
#define MAX_V 100 // 最大顶点数
// 图结构:邻接表
typedef struct Node {
int vertex;
struct Node* next;
} Node;
typedef struct Graph {
int V; // 顶点数
Node* adj[MAX_V]; // 邻接表
int* inDegree; // 入度数组
} Graph;
// 创建新节点
Node* createNode(int v) {
Node* newNode = (Node*)malloc(sizeof(Node));
newNode->vertex = v;
newNode->next = NULL;
return newNode;
}
// 初始化图
Graph* createGraph(int V) {
Graph* graph = (Graph*)malloc(sizeof(Graph));
graph->V = V;
graph->inDegree = (int*)calloc(V, sizeof(int)); // 初始化入度为0
for (int i = 0; i < V; i++) {
graph->adj[i] = NULL;
}
return graph;
}
// 添加边 u -> v
void addEdge(Graph* graph, int u, int v) {
Node* newNode = createNode(v);
newNode->next = graph->adj[u];
graph->adj[u] = newNode;
graph->inDegree[v]++; // v 的入度加1
}
// Kahn 算法实现拓扑排序
void topologicalSort(Graph* graph) {
int V = graph->V;
int* result = (int*)malloc(V * sizeof(int));
int index = 0;
// 模拟队列(用数组+front/rear)
int queue[MAX_V];
int front = 0, rear = 0;
// 将所有入度为0的顶点入队
for (int i = 0; i < V; i++) {
if (graph->inDegree[i] == 0) {
queue[rear++] = i;
}
}
while (front < rear) {
int u = queue[front++]; // 出队
result[index++] = u; // 加入结果
// 遍历 u 的所有邻接点
Node* temp = graph->adj[u];
while (temp) {
int v = temp->vertex;
graph->inDegree[v]--; // 入度减1
if (graph->inDegree[v] == 0) {
queue[rear++] = v; // 入度为0则入队
}
temp = temp->next;
}
}
// 判断是否有环
if (index != V) {
printf("图中存在环,无法拓扑排序!\n");
} else {
printf("拓扑序列: ");
for (int i = 0; i < V; i++) {
printf("%d ", result[i]);
}
printf("\n");
}
free(result);
}✅ 说明:
- 顶点编号从
0到V-1- 使用数组模拟队列(简化)
- 时间复杂度: O(V+E)O(V+E)
5.3.1.3 Java 实现(Kahn 算法)
java
import java.util.*;
public class TopologicalSort {
// 使用邻接表表示图
private static class Graph {
int V;
List<List<Integer>> adj;
int[] inDegree;
public Graph(int V) {
this.V = V;
adj = new ArrayList<>(V);
inDegree = new int[V];
for (int i = 0; i < V; i++) {
adj.add(new ArrayList<>());
}
}
public void addEdge(int u, int v) {
adj.get(u).add(v);
inDegree[v]++; // v 的入度加1
}
}
// Kahn 算法
public static void topologicalSort(Graph graph) {
int V = graph.V;
Queue<Integer> queue = new LinkedList<>();
List<Integer> result = new ArrayList<>();
// 将所有入度为0的顶点入队
for (int i = 0; i < V; i++) {
if (graph.inDegree[i] == 0) {
queue.offer(i);
}
}
while (!queue.isEmpty()) {
int u = queue.poll();
result.add(u);
// 遍历 u 的所有邻接点
for (int v : graph.adj.get(u)) {
graph.inDegree[v]--;
if (graph.inDegree[v] == 0) {
queue.offer(v);
}
}
}
// 判断是否有环
if (result.size() != V) {
System.out.println("图中存在环,无法拓扑排序!");
} else {
System.out.println("拓扑序列: " + result);
}
}
// 测试示例
public static void main(String[] args) {
Graph g = new Graph(5);
g.addEdge(0, 1);
g.addEdge(0, 2);
g.addEdge(1, 3);
g.addEdge(2, 3);
g.addEdge(3, 4);
topologicalSort(g); // 输出: [0, 1, 2, 3, 4] 或 [0, 2, 1, 3, 4]
}
}✅ 说明:
- 使用
ArrayList存储邻接表- 使用
Queue实现 FIFO- 自动处理多解情况(顺序由队列决定)
5.3.2 DFS 算法
5.3.2.1 算法思想
- 对每个未访问节点进行深度优先搜索(DFS)
- 在 递归回溯时(后序位置) 将节点加入结果(如栈或列表)
- 最终结果需 逆序输出 才是合法拓扑序列
- 若在 DFS 中遇到 正在访问的节点(灰色节点) → 存在环,无法拓扑排序
✅ 核心:后序遍历 + 逆序 = 拓扑序
5.3.2.2 C 语言实现(DFS 拓扑排序)
c
#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>
#define MAX_V 100
// 图结构:邻接表
typedef struct Node {
int vertex;
struct Node* next;
} Node;
typedef struct Graph {
int V;
Node* adj[MAX_V];
} Graph;
// 创建新节点
Node* createNode(int v) {
Node* newNode = (Node*)malloc(sizeof(Node));
newNode->vertex = v;
newNode->next = NULL;
return newNode;
}
// 初始化图
Graph* createGraph(int V) {
Graph* graph = (Graph*)malloc(sizeof(Graph));
graph->V = V;
for (int i = 0; i < V; i++) {
graph->adj[i] = NULL;
}
return graph;
}
// 添加有向边 u -> v
void addEdge(Graph* graph, int u, int v) {
Node* newNode = createNode(v);
newNode->next = graph->adj[u];
graph->adj[u] = newNode;
}
// DFS 辅助函数
bool dfsUtil(Graph* graph, int u, bool visited[], bool recStack[], int result[], int* index) {
visited[u] = true;
recStack[u] = true; // 标记为"正在递归中"(灰色)
// 遍历所有邻接点
Node* temp = graph->adj[u];
while (temp != NULL) {
int v = temp->vertex;
if (!visited[v]) {
if (!dfsUtil(graph, v, visited, recStack, result, index)) {
return false; // 子调用发现环
}
} else if (recStack[v]) {
// 遇到正在递归中的节点 → 有环
return false;
}
temp = temp->next;
}
recStack[u] = false; // 回溯,标记为"已完成"(黑色)
result[(*index)++] = u; // 后序位置:加入结果
return true;
}
// 主函数:拓扑排序(DFS)
void topologicalSortDFS(Graph* graph) {
int V = graph->V;
bool visited[MAX_V] = {false};
bool recStack[MAX_V] = {false}; // 递归栈标记(用于检测环)
int* result = (int*)malloc(V * sizeof(int));
int index = 0;
// 对每个未访问节点进行 DFS
for (int i = 0; i < V; i++) {
if (!visited[i]) {
if (!dfsUtil(graph, i, visited, recStack, result, &index)) {
printf("图中存在环,无法进行拓扑排序!\n");
free(result);
return;
}
}
}
// 输出:逆序打印(因为是后序收集)
printf("拓扑序列: ");
for (int i = V - 1; i >= 0; i--) {
printf("%d ", result[i]);
}
printf("\n");
free(result);
}
// 测试示例
int main() {
Graph* g = createGraph(5);
addEdge(g, 0, 1);
addEdge(g, 0, 2);
addEdge(g, 1, 3);
addEdge(g, 2, 3);
addEdge(g, 3, 4);
topologicalSortDFS(g); // 可能输出: 0 2 1 3 4 或 0 1 2 3 4(取决于邻接表顺序)
return 0;
}✅ 说明:
recStack[]用于检测回边(back edge),即环- 结果在
result[]中是逆拓扑序,需从后往前输出- 时间复杂度: O(V+E)O(V+E)
5.3.2.3 Java 实现(DFS 拓扑排序)
java
import java.util.*;
public class TopoSortDFS {
static class Graph {
int V;
List<List<Integer>> adj;
public Graph(int V) {
this.V = V;
adj = new ArrayList<>(V);
for (int i = 0; i < V; i++) {
adj.add(new ArrayList<>());
}
}
public void addEdge(int u, int v) {
adj.get(u).add(v);
}
}
// DFS 辅助函数
private static boolean dfsUtil(Graph g, int u, boolean[] visited,
boolean[] recStack, Stack<Integer> stack) {
visited[u] = true;
recStack[u] = true; // 标记为"正在访问"
for (int v : g.adj.get(u)) {
if (!visited[v]) {
if (!dfsUtil(g, v, visited, recStack, stack)) {
return false; // 子调用发现环
}
} else if (recStack[v]) {
return false; // 发现环(回边)
}
}
recStack[u] = false;
stack.push(u); // 后序位置压栈
return true;
}
// 主函数:拓扑排序(DFS)
public static void topologicalSortDFS(Graph g) {
int V = g.V;
boolean[] visited = new boolean[V];
boolean[] recStack = new boolean[V]; // 递归栈标记
Stack<Integer> stack = new Stack<>();
for (int i = 0; i < V; i++) {
if (!visited[i]) {
if (!dfsUtil(g, i, visited, recStack, stack)) {
System.out.println("图中存在环,无法进行拓扑排序!");
return;
}
}
}
// 输出栈中内容(即拓扑序列)
System.out.print("拓扑序列: ");
while (!stack.isEmpty()) {
System.out.print(stack.pop() + " ");
}
System.out.println();
}
// 测试
public static void main(String[] args) {
Graph g = new Graph(5);
g.addEdge(0, 1);
g.addEdge(0, 2);
g.addEdge(1, 3);
g.addEdge(2, 3);
g.addEdge(3, 4);
topologicalSortDFS(g); // 输出: 0 1 2 3 4 或 0 2 1 3 4(取决于遍历顺序)
}
}✅ 说明:
- 使用
Stack自动实现"后进先出",无需手动逆序recStack数组用于环检测(经典三色标记法简化版)- 若图不连通,仍能正确处理(主循环遍历所有顶点)
5.3.3 算法对比
| 特性 | Kahn 算法 | DFS 算法 |
|---|---|---|
| 数据结构 | 队列 + 入度数组 | 递归栈 + 访问标记 |
| 环检测 | 结果长度 < V | 遇到 recStack[v] == true |
| 输出顺序 | 直接正序 | 需逆序(或用栈) |
| 多解处理 | 队列顺序决定 | 邻接表遍历顺序决定 |
| 408 偏好 | ✅ 更常考 | 理论重要 |
六 考点跟踪
| 年份 | 题号 | 考查内容 | CSDN 参考链接 | VX参考链接 |
|---|---|---|---|---|
| 2010 | 第8题 | 拓扑排序个数 | ||
| 2021 | 第8题 | Dijkstra 最短路径 | ||
| 2022 | 第7题 | AOE 最大余量活动 |
说明 :本文内容基于公开资料整理,参考了包括但不限于《数据结构》(严蔚敏)、《计算机操作系统》(汤小丹)、《计算机网络》(谢希仁)、《计算机组成原理》(唐朔飞)等国内高校经典教材,以及其他国际权威著作。同时,借鉴了王道、天勤、启航等机构出版的计算机专业考研辅导系列丛书 中的知识体系框架与典型题型分析思路。文中所有观点、例题解析及文字表述均为作者结合自身理解进行的归纳与重述,未直接复制任何出版物原文。内容仅用于学习交流,若有引用不当或疏漏之处,敬请指正。