动态规划-打家劫舍I-II

独自破碎E2026-01-25 10:50

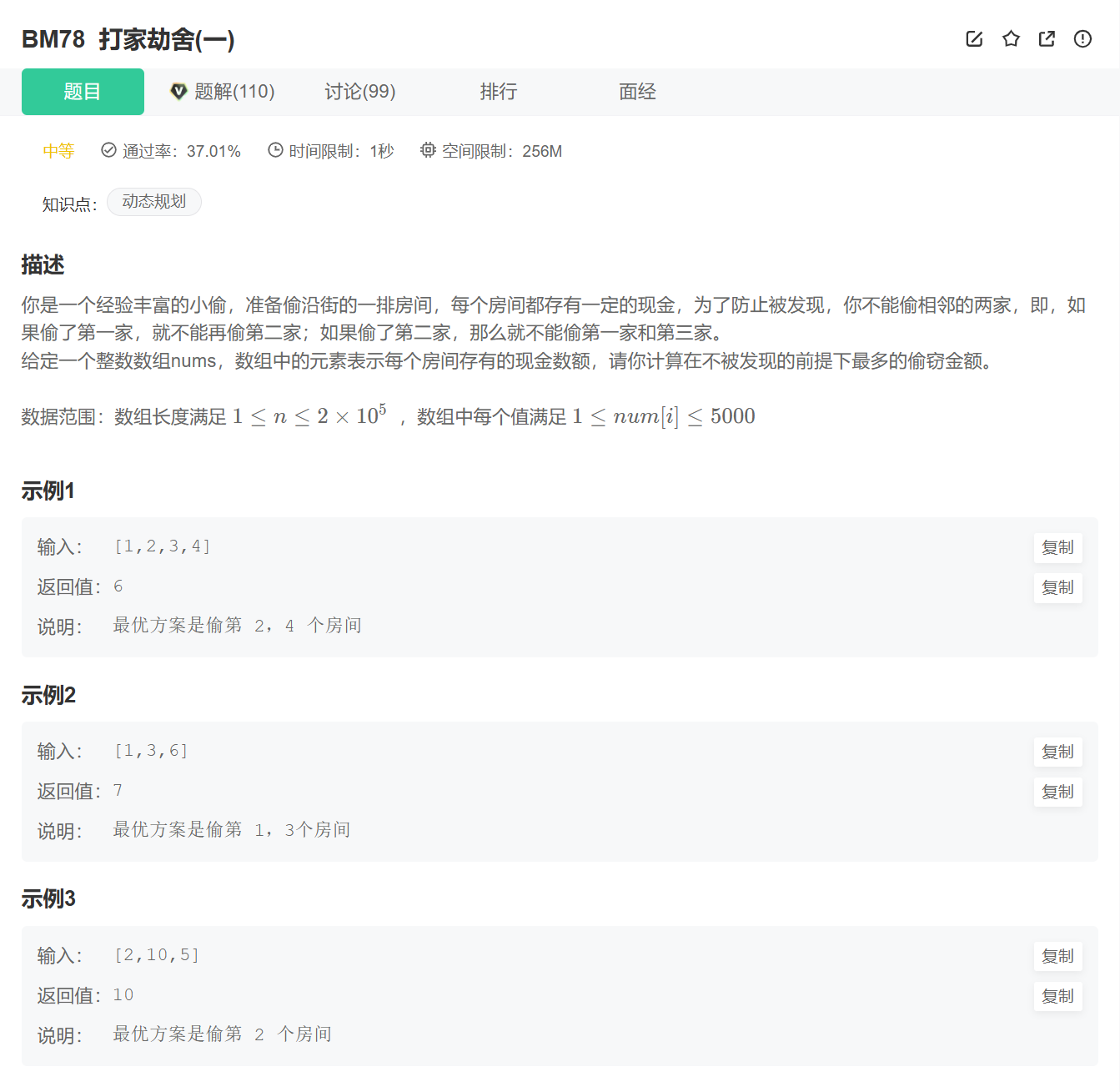
求解代码

java 复制代码

public int rob (int[] nums){
        int[] memo = new int[nums.length+1];
        Arrays.fill(memo, -1);
        return dp(nums,0, memo);
    }

    private int dp(int[] nums,int start,int[] memo){
        if(start>=nums.length){
            return 0;
        }

        if(memo[start]!=-1){
            return memo[start];
        }
        int ans = Math.max(dp(nums, start+1,memo),nums[start]+dp(nums, start+2,memo));
        memo[start]= ans;
        return ans;
    }

小贴士

记忆化存储+自顶向下

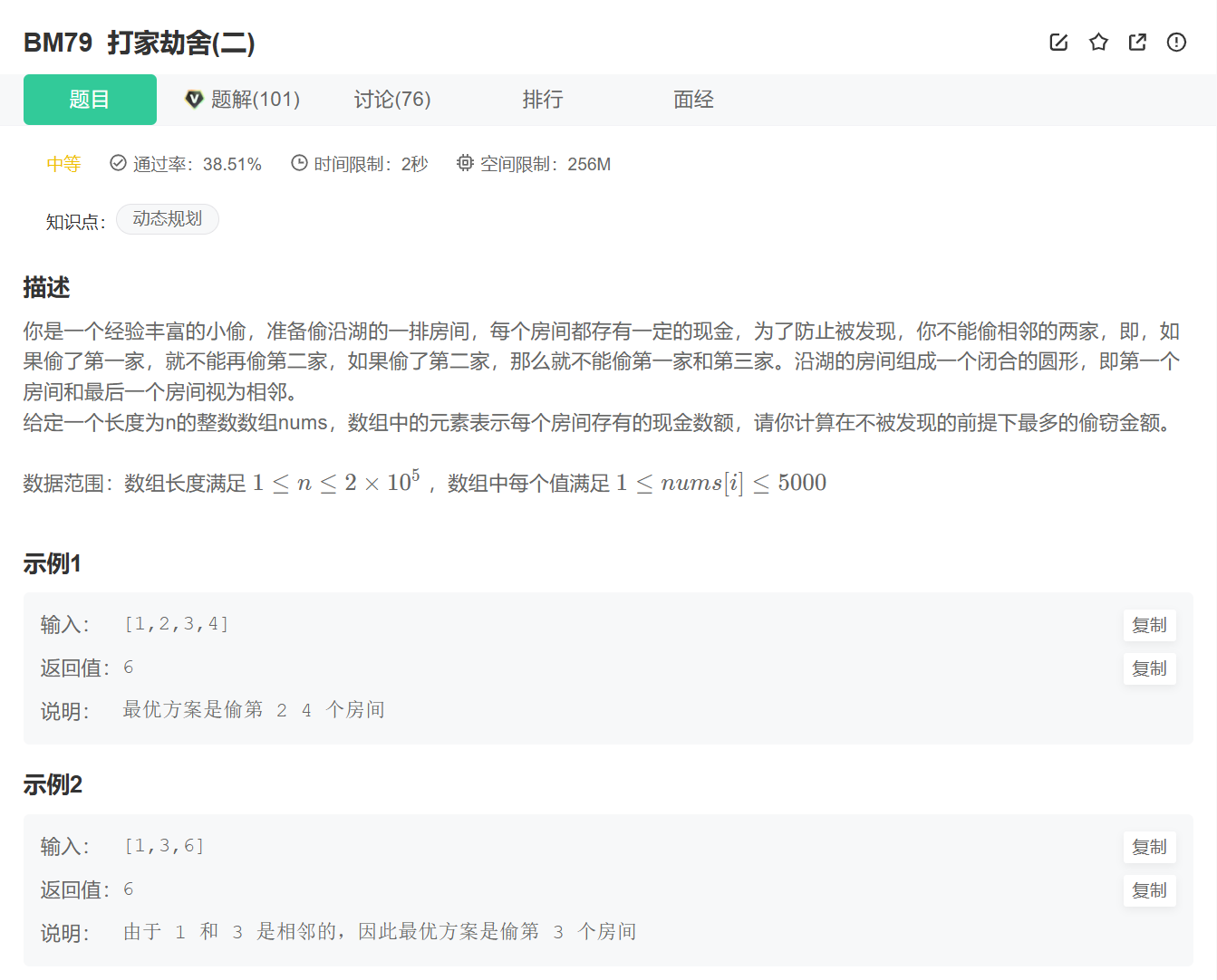
求解代码

java 复制代码

public int rob(int[] nums) {
        int n = nums.length;
        int[] memo1 = new int[n + 1];
        int[] memo2 = new int[n + 1];
        Arrays.fill(memo1, -1);
        Arrays.fill(memo2, -1);
        int case1 = dp(nums, 0, n - 2, memo1);
        int case2 = dp(nums, 1, n - 1, memo2);
        return Math.max(case1, case2);
    }

    private int dp(int[] nums, int start, int end, int[] memo) {
        if (start > end) {
            return 0;
        }

        if (memo[start] != -1) {
            return memo[start];
        }
        int ans = Math.max(dp(nums, start + 1, end, memo), nums[start] + dp(nums,
                start + 2, end, memo));
        memo[start] = ans;
        return ans;
    }

小贴士

现在的情况是第一房间和最后一个房间也相当于是相邻的，不能同时抢。

那么，首尾房间不能同时被抢，只可能有三种不同情况：

都不被抢
第一个房间被抢最后一间不抢
最后一个房间被抢第一间不抢

不过，本题不需要三种情况都进行比较，因为房间里的钱数都是非负数，后两种情况对于房间的选择余地肯定比情况一大，所以只要比较情况二和情况三就行了。

代码也可以在【打家劫舍I】的【自顶向下+记忆化存储】基础上进行修改。

需要注意的是独立的子问题必须使用独立的记忆化缓存，不能共用，不然会造成缓存被覆盖的问题，所以这里需要使用两个memory。