耦合传输线分析学习笔记(七)不对称耦合微带线Y参数矩阵推导与应用

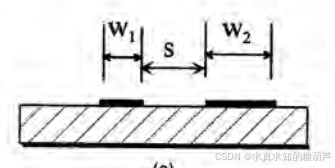
图1 不对称耦合微带线

 这里讨论的是如图1剖面不对称，在图2中左右1和3端口、2和4端口满足对称条件

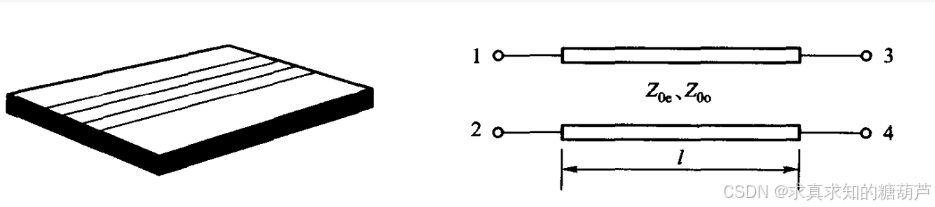
图2 端口顺序定义

参考前面的6篇文章中我们推出了如下公式
U1U2=11k−1kUeIUoI(1) \left\\begin{array}{l} U_{1} \\\\ U_{2} \\end{array}\\right=\left\\begin{array}{cc} 1 \& 1 \\\\ k \& -\\frac{1}{k} \\end{array}\\right\left\\begin{array}{l} U_{\\mathrm{e}}\^{I} \\\\ U_{\\mathrm{o}}\^{I} \\end{array}\\right \quad(1) U1U2=1k1−k1UeIUoI(1)

U3U4=11k−1kUeIIUoII(2) \left\\begin{array}{l} U_{3} \\\\ U_{4} \\end{array}\\right=\left\\begin{array}{cc} 1 \& 1 \\\\ k \& -\\frac{1}{k} \\end{array}\\right\left\\begin{array}{l} U_{\\mathrm{e}}\^{II} \\\\ U_{\\mathrm{o}}\^{II} \\end{array}\\right \quad(2) U3U4=1k1−k1UeIIUoII(2)

IeIIoI=kk2+11k1k−1I1I2(3) \left\\begin{array}{l} I_{\\mathrm{e}}\^{I} \\\\ I_{\\mathrm{o}}\^{I} \\end{array}\\right=\frac{k}{k^{2}+1}\left\\begin{array}{cc} \\frac{1}{k} \& 1 \\\\ k \& -1 \\end{array}\\right\left\\begin{array}{l} I_{1} \\\\ I_{2} \\end{array}\\right \quad(3) IeIIoI=k2+1kk1k1−1I1I2(3)

IeIIIoII=kk2+11k1k−1I3I4(4) \left\\begin{array}{l} I_{\\mathrm{e}}\^{II} \\\\ I_{\\mathrm{o}}\^{II} \\end{array}\\right=\frac{k}{k^{2}+1}\left\\begin{array}{cc} \\frac{1}{k} \& 1 \\\\ k \& -1 \\end{array}\\right\left\\begin{array}{l} I_{3} \\\\ I_{4} \\end{array}\\right \quad(4) IeIIIoII=k2+1kk1k1−1I3I4(4)

传输线ABCD矩阵可以由如下二式表示
Ue1Ie1=cos⁡θejZ0esin⁡θejY0esin⁡θecos⁡θeUeIIIeII(5) \begin{bmatrix} U_e^1 \\ I_e^1 \end{bmatrix} = \begin{bmatrix} \cos \theta_e & j Z_{0e} \sin \theta_e \\ j Y_{0e} \sin \theta_e & \cos \theta_e \end{bmatrix} \begin{bmatrix} U_e^{II} \\ I_e^{II} \end{bmatrix}\qquad(5) Ue1Ie1=cosθejY0esinθejZ0esinθecosθeUeIIIeII(5)
Uo1Io1=cos⁡θojZ0osin⁡θojY0osin⁡θocos⁡θoUoIIIoII(6) \begin{bmatrix} U_o^1 \\ I_o^1 \end{bmatrix} = \begin{bmatrix} \cos \theta_o & j Z_{0o} \sin \theta_o \\ j Y_{0o} \sin \theta_o & \cos \theta_o \end{bmatrix} \begin{bmatrix} U_o^{II} \\ I_o^{II} \end{bmatrix}\qquad(6) Uo1Io1=cosθojY0osinθojZ0osinθocosθoUoIIIoII(6)

（这里 Y0e=1/Z0e,Y0o=1/Z0oY_{0e} = 1/Z_{0e}, Y_{0o} = 1/Z_{0o}Y0e=1/Z0e,Y0o=1/Z0o）

 分析思路：采用类似上一节的方法，我们已经推出了耦合微带线的四端口A参数和Z参数矩阵，下面我们需要将去耦后的传输线ABCD参数转换为二端口的Y参数矩阵。

 全过程如下通过奇偶模分解法，将四端口网络分解为偶模和奇模两个独立的传输线二端口网络，然后通过前后两个变换矩阵组合得到整体Y参数。

1. 奇偶模分解法

 对于如图2所示的不对称耦合微带线（端口1和3、端口2和4满足对称条件），通过奇偶模分解法将四端口网络分解为偶模（even mode）和奇模（odd mode）两个独立的二端口网络。偶模和奇模具有不同的特性阻抗（Z0eZ_{0e}Z0e、Z0oZ_{0o}Z0o）同时由于微带线不均匀，奇偶模相速度不同具有不同电长度（θe\theta_eθe、θo\theta_oθo），其中 Y0e=1/Z0eY_{0e} = 1/Z_{0e}Y0e=1/Z0e，Y0o=1/Z0oY_{0o} = 1/Z_{0o}Y0o=1/Z0o。

2. 电压与电流的变换关系

端口电压与奇偶模电压的关系由变换矩阵定义：
U1U2=11k−1kUeIUoI(1) \begin{bmatrix} U_1 \\ U_2 \end{bmatrix} = \begin{bmatrix} 1 & 1 \\ k & -\frac{1}{k} \end{bmatrix} \begin{bmatrix} U_e^I \\ U_o^I \end{bmatrix} \quad (1) U1U2=1k1−k1UeIUoI(1)
U3U4=11k−1kUeIIUoII(2) \begin{bmatrix} U_3 \\ U_4 \end{bmatrix} = \begin{bmatrix} 1 & 1 \\ k & -\frac{1}{k} \end{bmatrix} \begin{bmatrix} U_e^{II} \\ U_o^{II} \end{bmatrix} \quad (2) U3U4=1k1−k1UeIIUoII(2)

端口电流与奇偶模电流的关系：
IeIIoI=kk2+11k1k−1I1I2(3) \begin{bmatrix} I_e^I \\ I_o^I \end{bmatrix} = \frac{k}{k^2+1} \begin{bmatrix} \frac{1}{k} & 1 \\ k & -1 \end{bmatrix} \begin{bmatrix} I_1 \\ I_2 \end{bmatrix} \quad (3) IeIIoI=k2+1kk1k1−1I1I2(3)
IeIIIoII=kk2+11k1k−1I3I4(4) \begin{bmatrix} I_e^{II} \\ I_o^{II} \end{bmatrix} = \frac{k}{k^2+1} \begin{bmatrix} \frac{1}{k} & 1 \\ k & -1 \end{bmatrix} \begin{bmatrix} I_3 \\ I_4 \end{bmatrix} \quad (4) IeIIIoII=k2+1kk1k1−1I3I4(4)

设四端口网络的端口电压和电流（定义所有电流流入网络为正）为：
Vp=U1,U2,U3,U4T,Ip=I1,I2,I3,I4T. \mathbf{V}_p = U_1, U_2, U_3, U_4^T, \quad \mathbf{I}_p = I_1, I_2, I_3, I_4^T. Vp=U1,U2,U3,U4T,Ip=I1,I2,I3,I4T.

奇偶模电压、电流定义为：
Vm=UeI,UeII,UoI,UoIIT,Im=IeI,IeII,IoI,IoIIT. \mathbf{V}_m = U_e\^I, U_e\^{II}, U_o\^I, U_o\^{II}^T, \quad \mathbf{I}_m = I_e\^I, I_e\^{II}, I_o\^I, I_o\^{II}^T. Vm=UeI,UeII,UoI,UoIIT,Im=IeI,IeII,IoI,IoIIT.

根据公式(1)-(4)构建全局变换矩阵：

Vp=T⋅Vm,Im=Q⋅Ip \mathbf{V}_p = \mathbf{T} \cdot \mathbf{V}_m, \quad \mathbf{I}_m = \mathbf{Q} \cdot \mathbf{I}_p Vp=T⋅Vm,Im=Q⋅Ip

其中：

T=1010k0−1k001010k0−1k \mathbf{T} = \begin{bmatrix} 1 & 0 & 1 & 0 \\ k & 0 & -\frac{1}{k} & 0 \\ 0 & 1 & 0 & 1 \\ 0 & k & 0 & -\frac{1}{k} \end{bmatrix} T= 1k00001k1−k100001−k1

Q=kk2+11k100001k1k−10000k−1=T−1 \mathbf{Q} = \frac{k}{k^2+1} \begin{bmatrix} \frac{1}{k} & 1 & 0 & 0 \\ 0 & 0 & \frac{1}{k} & 1 \\ k & -1 & 0 & 0 \\ 0 & 0 & k & -1 \end{bmatrix}=T^{-1} Q=k2+1k k10k010−100k10k010−1 =T−1

则端口电压与奇偶模电压的关系为：
U1U2U3U4=1010k0−1k001010k0−1kUeIUeIIUoIUoII=T⋅Vm \begin{bmatrix} U_1 \\ U_2 \\ U_3 \\ U_4 \end{bmatrix} = \begin{bmatrix} 1 & 0 & 1 & 0 \\ k & 0 & -\frac{1}{k} & 0 \\ 0 & 1 & 0 & 1 \\ 0 & k & 0 & -\frac{1}{k} \end{bmatrix} \begin{bmatrix} U_e^I \\ U_e^{II} \\ U_o^I \\ U_o^{II} \end{bmatrix} = \mathbf{T} \cdot \mathbf{V}_m U1U2U3U4 = 1k00001k1−k100001−k1 UeIUeIIUoIUoII =T⋅Vm

端口电流与奇偶模电流的关系为：
IeIIeIIIoIIoII=kk2+11k100001k1k−10000k−1I1I2I3I4=Q⋅Ip \begin{bmatrix} I_e^I \\ I_e^{II} \\ I_o^I \\ I_o^{II} \end{bmatrix} = \frac{k}{k^2+1} \begin{bmatrix} \frac{1}{k} & 1 & 0 & 0 \\ 0 & 0 & \frac{1}{k} & 1 \\ k & -1 & 0 & 0 \\ 0 & 0 & k & -1 \end{bmatrix} \begin{bmatrix} I_1 \\ I_2 \\ I_3 \\ I_4 \end{bmatrix} = \mathbf{Q} \cdot \mathbf{I}_p IeIIeIIIoIIoII =k2+1k k10k010−100k10k010−1 I1I2I3I4 =Q⋅Ip

3. 奇偶模网络的导纳矩阵

3.1 偶模二端口网络的导纳矩阵

偶模网络ABCD参数为：

UeIIeI\]=\[cos⁡θejZ0esin⁡θejY0esin⁡θecos⁡θe\]\[UeIIIeII\] \\begin{bmatrix} U_e\^I \\\\ I_e\^I \\end{bmatrix} = \\begin{bmatrix} \\cos \\theta_e \& j Z_{0e} \\sin \\theta_e \\\\ j Y_{0e} \\sin \\theta_e \& \\cos \\theta_e \\end{bmatrix} \\begin{bmatrix} U_e\^{II} \\\\ I_e\^{II} \\end{bmatrix} \[UeIIeI\]=\[cosθejY0esinθejZ0esinθecosθe\]\[UeIIIeII

转换为Y参数矩阵：

Ye=Y11eY12eY21eY22e=−jY0ecot⁡θe−csc⁡θe−csc⁡θecot⁡θe \mathbf{Y}{e} = \begin{bmatrix} Y{11e} & Y_{12e} \\ Y_{21e} & Y_{22e} \end{bmatrix} = -j Y_{0e} \begin{bmatrix} \cot \theta_e & -\csc \theta_e \\ -\csc \theta_e & \cot \theta_e \end{bmatrix} Ye=Y11eY21eY12eY22e=−jY0ecotθe−cscθe−cscθecotθe

为方便计算我们可以定义：
Ce=−jY0ecot⁡θe,De=jY0ecsc⁡θe C_e = -jY_{0e}\cot\theta_e, \quad D_e = jY_{0e}\csc\theta_e Ce=−jY0ecotθe,De=jY0ecscθe

则：
Ye=CeDeDeCe \mathbf{Y}_e = \begin{bmatrix} C_e & D_e \\ D_e & C_e \end{bmatrix} Ye=CeDeDeCe

3.2 奇模二端口网络的导纳矩阵

奇模网络ABCD参数为：

UoIIoI\]=\[cos⁡θojZ0osin⁡θojY0osin⁡θocos⁡θo\]\[UoIIIoII\] \\begin{bmatrix} U_o\^I \\\\ I_o\^I \\end{bmatrix} = \\begin{bmatrix} \\cos \\theta_o \& j Z_{0o} \\sin \\theta_o \\\\ j Y_{0o} \\sin \\theta_o \& \\cos \\theta_o \\end{bmatrix} \\begin{bmatrix} U_o\^{II} \\\\ I_o\^{II} \\end{bmatrix} \[UoIIoI\]=\[cosθojY0osinθojZ0osinθocosθo\]\[UoIIIoII

转换为Y参数矩阵：

Yo=Y11oY12oY21oY22o=−jY0ocot⁡θo−csc⁡θo−csc⁡θocot⁡θo \mathbf{Y}{o} = \begin{bmatrix} Y{11o} & Y_{12o} \\ Y_{21o} & Y_{22o} \end{bmatrix} = -j Y_{0o} \begin{bmatrix} \cot \theta_o & -\csc \theta_o \\ -\csc \theta_o & \cot \theta_o \end{bmatrix} Yo=Y11oY21oY12oY22o=−jY0ocotθo−cscθo−cscθocotθo

同偶模定义：
Co=−jY0ocot⁡θo,Do=jY0ocsc⁡θo C_o = -jY_{0o}\cot\theta_o, \quad D_o = jY_{0o}\csc\theta_o Co=−jY0ocotθo,Do=jY0ocscθo

则：
Yo=CoDoDoCo \mathbf{Y}_o = \begin{bmatrix} C_o & D_o \\ D_o & C_o \end{bmatrix} Yo=CoDoDoCo

3.3 组合奇偶模导纳矩阵

由于偶模和奇模网络相互独立，组合成块对角矩阵：

Im=YmVm,其中Ym=Ye00Yo \mathbf{I}_m = \mathbf{Y}_m \mathbf{V}m, \quad \text{其中} \quad \mathbf{Y}m = \begin{bmatrix} \mathbf{Y}{e} & \mathbf{0} \\ \mathbf{0} & \mathbf{Y}{o} \end{bmatrix} Im=YmVm,其中Ym=Ye00Yo

4. 四端口网络Y参数矩阵推导

4.1 建立端口导纳矩阵关系

由变换关系联立：

Im=QIp,Im=YmVm,Vm=T−1Vp \mathbf{I}_m = \mathbf{Q} \mathbf{I}_p, \quad \mathbf{I}_m = \mathbf{Y}_m \mathbf{V}_m, \quad \mathbf{V}_m = \mathbf{T}^{-1} \mathbf{V}_p Im=QIp,Im=YmVm,Vm=T−1Vp

代入得：

QIp=YmT−1Vp \mathbf{Q} \mathbf{I}_p = \mathbf{Y}_m \mathbf{T}^{-1} \mathbf{V}_p QIp=YmT−1Vp

两边左乘 Q−1\mathbf{Q}^{-1}Q−1，

Ip=Q−1YmT−1Vp \mathbf{I}_p = \mathbf{Q}^{-1}\mathbf{Y}_m \mathbf{T}^{-1} \mathbf{V}_p Ip=Q−1YmT−1Vp

因此四端口Y参数矩阵为：
Y=Q−1⋅Ym⋅T−1 \mathbf{Y} = \mathbf{Q}^{-1} \cdot \mathbf{Y}_m \cdot \mathbf{T}^{-1} Y=Q−1⋅Ym⋅T−1

4.2 矩阵乘法计算

计算 M=TYm\mathbf{M} = \mathbf{T} \mathbf{Y}_mM=TYm：

M=1010k0−1k001010k0−1kCeDe00DeCe0000CoDo00DoCo=CeDeCoDokCekDe−Cok−DokDeCeDoCokDekCe−Dok−Cok \mathbf{M} = \begin{bmatrix} 1 & 0 & 1 & 0 \\ k & 0 & -\frac{1}{k} & 0 \\ 0 & 1 & 0 & 1 \\ 0 & k & 0 & -\frac{1}{k} \end{bmatrix} \begin{bmatrix} C_e & D_e & 0 & 0 \\ D_e & C_e & 0 & 0 \\ 0 & 0 & C_o & D_o \\ 0 & 0 & D_o & C_o \end{bmatrix} =\begin{bmatrix} C_e & D_e & C_o & D_o \\ kC_e & kD_e & -\frac{C_o}{k} & -\frac{D_o}{k} \\ D_e & C_e & D_o & C_o \\ kD_e & kC_e & -\frac{D_o}{k} & -\frac{C_o}{k} \end{bmatrix} M= 1k00001k1−k100001−k1 CeDe00DeCe0000CoDo00DoCo = CekCeDekDeDekDeCekCeCo−kCoDo−kDoDo−kDoCo−kCo

然后计算 Y=MT−1=1k2+1MT~\mathbf{Y} = \mathbf{M} \mathbf{T}^{-1} = \frac{1}{k^2+1} \mathbf{M} \tilde{\mathbf{T}}Y=MT−1=k2+11MT~，其中 T~=1k00001kk2−k0000k2−k\tilde{\mathbf{T}} = \begin{bmatrix} 1 & k & 0 & 0 \\ 0 & 0 & 1 & k \\ k^2 & -k & 0 & 0 \\ 0 & 0 & k^2 & -k \end{bmatrix}T~= 10k20k0−k0010k20k0−k 。

计算过程如下：

第一个元素 Y11Y_{11}Y11：
Y11=1k2+1Ce⋅1+De⋅0+Co⋅k2+Do⋅0=Ce+k2Cok2+1 Y_{11} = \frac{1}{k^2+1} \left C_e \\cdot 1 + D_e \\cdot 0 + C_o \\cdot k\^2 + D_o \\cdot 0 \\right = \frac{C_e + k^2 C_o}{k^2+1} Y11=k2+11Ce⋅1+De⋅0+Co⋅k2+Do⋅0=k2+1Ce+k2Co

第二个元素 Y12Y_{12}Y12：
Y12=1k2+1Ce⋅k+De⋅0+Co⋅(−k)+Do⋅0=k(Ce−Co)k2+1 Y_{12} = \frac{1}{k^2+1} \left C_e \\cdot k + D_e \\cdot 0 + C_o \\cdot (-k) + D_o \\cdot 0 \\right = \frac{k(C_e - C_o)}{k^2+1} Y12=k2+11Ce⋅k+De⋅0+Co⋅(−k)+Do⋅0=k2+1k(Ce−Co)

第三个元素 Y13Y_{13}Y13：
Y13=1k2+1Ce⋅0+De⋅1+Co⋅0+Do⋅k2=De+k2Dok2+1 Y_{13} = \frac{1}{k^2+1} \left C_e \\cdot 0 + D_e \\cdot 1 + C_o \\cdot 0 + D_o \\cdot k\^2 \\right = \frac{D_e + k^2 D_o}{k^2+1} Y13=k2+11Ce⋅0+De⋅1+Co⋅0+Do⋅k2=k2+1De+k2Do

第四个元素 Y14Y_{14}Y14：
Y14=1k2+1Ce⋅0+De⋅k+Co⋅0+Do⋅(−k)=k(De−Do)k2+1 Y_{14} = \frac{1}{k^2+1} \left C_e \\cdot 0 + D_e \\cdot k + C_o \\cdot 0 + D_o \\cdot (-k) \\right = \frac{k(D_e - D_o)}{k^2+1} Y14=k2+11Ce⋅0+De⋅k+Co⋅0+Do⋅(−k)=k2+1k(De−Do)

类似地，可以计算其他元素。最终得到四端口Y参数矩阵：

Y=1k2+1Ce+k2Cok(Ce−Co)De+k2Dok(De−Do)k(Ce−Co)k2Ce+Cok(De−Do)k2De+DoDe+k2Dok(De−Do)Ce+k2Cok(Ce−Co)k(De−Do)k2De+Dok(Ce−Co)k2Ce+Co \mathbf{Y} = \frac{1}{k^2+1} \begin{bmatrix} C_e + k^2 C_o & k(C_e - C_o) & D_e + k^2 D_o & k(D_e - D_o) \\ k(C_e - C_o) & k^2 C_e + C_o & k(D_e - D_o) & k^2 D_e + D_o \\ D_e + k^2 D_o & k(D_e - D_o) & C_e + k^2 C_o & k(C_e - C_o) \\ k(D_e - D_o) & k^2 D_e + D_o & k(C_e - C_o) & k^2 C_e + C_o \end{bmatrix} Y=k2+11 Ce+k2Cok(Ce−Co)De+k2Dok(De−Do)k(Ce−Co)k2Ce+Cok(De−Do)k2De+DoDe+k2Dok(De−Do)Ce+k2Cok(Ce−Co)k(De−Do)k2De+Dok(Ce−Co)k2Ce+Co

5. 最终结果

将 Ce,De,Co,DoC_e, D_e, C_o, D_oCe,De,Co,Do 代入，得到完整的不对称耦合微带线Y参数矩阵：

Y=Y11Y12Y13Y14Y21Y22Y23Y24Y13Y23Y11Y12Y14Y24Y12Y22 \mathbf{Y} = \begin{bmatrix} Y_{11} & Y_{12} & Y_{13} & Y_{14} \\ Y_{21} & Y_{22} & Y_{23} & Y_{24} \\ Y_{13} & Y_{23} & Y_{11} & Y_{12} \\ Y_{14} & Y_{24} & Y_{12} & Y_{22} \end{bmatrix} Y= Y11Y21Y13Y14Y12Y22Y23Y24Y13Y23Y11Y12Y14Y24Y12Y22

其中：

Y11=Y33=1k2+1(−jY0ecot⁡θe−jk2Y0ocot⁡θo)Y22=Y44=1k2+1(−jk2Y0ecot⁡θe−jY0ocot⁡θo)Y12=Y21=Y34=Y43=kk2+1(−jY0ecot⁡θe+jY0ocot⁡θo)Y13=Y31=1k2+1(jY0ecsc⁡θe+jk2Y0ocsc⁡θo)Y14=Y41=Y23=Y32=kk2+1(jY0ecsc⁡θe−jY0ocsc⁡θo)Y24=Y42=1k2+1(jk2Y0ecsc⁡θe+jY0ocsc⁡θo) \begin{aligned} Y_{11} = Y_{33} &= \frac{1}{k^2+1} \left( -jY_{0e}\cot\theta_e - jk^2 Y_{0o}\cot\theta_o \right) \\ Y_{22} = Y_{44} &= \frac{1}{k^2+1} \left( -jk^2 Y_{0e}\cot\theta_e - jY_{0o}\cot\theta_o \right) \\ Y_{12} = Y_{21} = Y_{34} = Y_{43} &= \frac{k}{k^2+1} \left( -jY_{0e}\cot\theta_e + jY_{0o}\cot\theta_o \right) \\ Y_{13} = Y_{31} &= \frac{1}{k^2+1} \left( jY_{0e}\csc\theta_e + jk^2 Y_{0o}\csc\theta_o \right) \\ Y_{14} = Y_{41} = Y_{23} = Y_{32} &= \frac{k}{k^2+1} \left( jY_{0e}\csc\theta_e - jY_{0o}\csc\theta_o \right) \\ Y_{24} = Y_{42} &= \frac{1}{k^2+1} \left( jk^2 Y_{0e}\csc\theta_e + jY_{0o}\csc\theta_o \right) \end{aligned} Y11=Y33Y22=Y44Y12=Y21=Y34=Y43Y13=Y31Y14=Y41=Y23=Y32Y24=Y42=k2+11(−jY0ecotθe−jk2Y0ocotθo)=k2+11(−jk2Y0ecotθe−jY0ocotθo)=k2+1k(−jY0ecotθe+jY0ocotθo)=k2+11(jY0ecscθe+jk2Y0ocscθo)=k2+1k(jY0ecscθe−jY0ocscθo)=k2+11(jk2Y0ecscθe+jY0ocscθo)

 以上对称关系反映了图2中耦合线虽然上下不对称但是满足左右对称性，即端口1和3、端口2和4的结构对称性。
Y=1k2+1−j(Y0ecot⁡θe+k2Y0ocot⁡θo)−jk(Y0ecot⁡θe−Y0ocot⁡θo)j(Y0ecsc⁡θe+k2Y0ocsc⁡θo)jk(Y0ecsc⁡θe−Y0ocsc⁡θo)−jk(Y0ecot⁡θe−Y0ocot⁡θo)−j(k2Y0ecot⁡θe+Y0ocot⁡θo)jk(Y0ecsc⁡θe−Y0ocsc⁡θo)j(k2Y0ecsc⁡θe+Y0ocsc⁡θo)j(Y0ecsc⁡θe+k2Y0ocsc⁡θo)jk(Y0ecsc⁡θe−Y0ocsc⁡θo)−j(Y0ecot⁡θe+k2Y0ocot⁡θo)−jk(Y0ecot⁡θe−Y0ocot⁡θo)jk(Y0ecsc⁡θe−Y0ocsc⁡θo)j(k2Y0ecsc⁡θe+Y0ocsc⁡θo)−jk(Y0ecot⁡θe−Y0ocot⁡θo)−j(k2Y0ecot⁡θe+Y0ocot⁡θo) \mathbf{Y} = \frac{1}{k^2+1} \begin{bmatrix} -j\left(Y_{0e}\cot\theta_e + k^2 Y_{0o}\cot\theta_o\right) & -jk\left(Y_{0e}\cot\theta_e - Y_{0o}\cot\theta_o\right) & j\left(Y_{0e}\csc\theta_e + k^2 Y_{0o}\csc\theta_o\right) & jk\left(Y_{0e}\csc\theta_e - Y_{0o}\csc\theta_o\right) \\8pt -jk\left(Y_{0e}\cot\theta_e - Y_{0o}\cot\theta_o\right) & -j\left(k^2 Y_{0e}\cot\theta_e + Y_{0o}\cot\theta_o\right) & jk\left(Y_{0e}\csc\theta_e - Y_{0o}\csc\theta_o\right) & j\left(k^2 Y_{0e}\csc\theta_e + Y_{0o}\csc\theta_o\right) \\8pt j\left(Y_{0e}\csc\theta_e + k^2 Y_{0o}\csc\theta_o\right) & jk\left(Y_{0e}\csc\theta_e - Y_{0o}\csc\theta_o\right) & -j\left(Y_{0e}\cot\theta_e + k^2 Y_{0o}\cot\theta_o\right) & -jk\left(Y_{0e}\cot\theta_e - Y_{0o}\cot\theta_o\right) \\8pt jk\left(Y_{0e}\csc\theta_e - Y_{0o}\csc\theta_o\right) & j\left(k^2 Y_{0e}\csc\theta_e + Y_{0o}\csc\theta_o\right) & -jk\left(Y_{0e}\cot\theta_e - Y_{0o}\cot\theta_o\right) & -j\left(k^2 Y_{0e}\cot\theta_e + Y_{0o}\cot\theta_o\right) \end{bmatrix} Y=k2+11 −j(Y0ecotθe+k2Y0ocotθo)−jk(Y0ecotθe−Y0ocotθo)j(Y0ecscθe+k2Y0ocscθo)jk(Y0ecscθe−Y0ocscθo)−jk(Y0ecotθe−Y0ocotθo)−j(k2Y0ecotθe+Y0ocotθo)jk(Y0ecscθe−Y0ocscθo)j(k2Y0ecscθe+Y0ocscθo)j(Y0ecscθe+k2Y0ocscθo)jk(Y0ecscθe−Y0ocscθo)−j(Y0ecotθe+k2Y0ocotθo)−jk(Y0ecotθe−Y0ocotθo)jk(Y0ecscθe−Y0ocscθo)j(k2Y0ecscθe+Y0ocscθo)−jk(Y0ecotθe−Y0ocotθo)−j(k2Y0ecotθe+Y0ocotθo)

=jk2+1−(Y0ecot⁡θe+k2Y0ocot⁡θo)−k(Y0ecot⁡θe−Y0ocot⁡θo)(Y0ecsc⁡θe+k2Y0ocsc⁡θo)k(Y0ecsc⁡θe−Y0ocsc⁡θo)−k(Y0ecot⁡θe−Y0ocot⁡θo)−(k2Y0ecot⁡θe+Y0ocot⁡θo)k(Y0ecsc⁡θe−Y0ocsc⁡θo)(k2Y0ecsc⁡θe+Y0ocsc⁡θo)(Y0ecsc⁡θe+k2Y0ocsc⁡θo)k(Y0ecsc⁡θe−Y0ocsc⁡θo)−(Y0ecot⁡θe+k2Y0ocot⁡θo)−k(Y0ecot⁡θe−Y0ocot⁡θo)k(Y0ecsc⁡θe−Y0ocsc⁡θo)(k2Y0ecsc⁡θe+Y0ocsc⁡θo)−k(Y0ecot⁡θe−Y0ocot⁡θo)−(k2Y0ecot⁡θe+Y0ocot⁡θo) = \frac{j}{k^2+1} \begin{bmatrix} -\left(Y_{0e}\cot\theta_e + k^2 Y_{0o}\cot\theta_o\right) & -k\left(Y_{0e}\cot\theta_e - Y_{0o}\cot\theta_o\right) & \left(Y_{0e}\csc\theta_e + k^2 Y_{0o}\csc\theta_o\right) & k\left(Y_{0e}\csc\theta_e - Y_{0o}\csc\theta_o\right) \\8pt -k\left(Y_{0e}\cot\theta_e - Y_{0o}\cot\theta_o\right) & -\left(k^2 Y_{0e}\cot\theta_e + Y_{0o}\cot\theta_o\right) & k\left(Y_{0e}\csc\theta_e - Y_{0o}\csc\theta_o\right) & \left(k^2 Y_{0e}\csc\theta_e + Y_{0o}\csc\theta_o\right) \\8pt \left(Y_{0e}\csc\theta_e + k^2 Y_{0o}\csc\theta_o\right) & k\left(Y_{0e}\csc\theta_e - Y_{0o}\csc\theta_o\right) & -\left(Y_{0e}\cot\theta_e + k^2 Y_{0o}\cot\theta_o\right) & -k\left(Y_{0e}\cot\theta_e - Y_{0o}\cot\theta_o\right) \\8pt k\left(Y_{0e}\csc\theta_e - Y_{0o}\csc\theta_o\right) & \left(k^2 Y_{0e}\csc\theta_e + Y_{0o}\csc\theta_o\right) & -k\left(Y_{0e}\cot\theta_e - Y_{0o}\cot\theta_o\right) & -\left(k^2 Y_{0e}\cot\theta_e + Y_{0o}\cot\theta_o\right) \end{bmatrix} =k2+1j −(Y0ecotθe+k2Y0ocotθo)−k(Y0ecotθe−Y0ocotθo)(Y0ecscθe+k2Y0ocscθo)k(Y0ecscθe−Y0ocscθo)−k(Y0ecotθe−Y0ocotθo)−(k2Y0ecotθe+Y0ocotθo)k(Y0ecscθe−Y0ocscθo)(k2Y0ecscθe+Y0ocscθo)(Y0ecscθe+k2Y0ocscθo)k(Y0ecscθe−Y0ocscθo)−(Y0ecotθe+k2Y0ocotθo)−k(Y0ecotθe−Y0ocotθo)k(Y0ecscθe−Y0ocscθo)(k2Y0ecscθe+Y0ocscθo)−k(Y0ecotθe−Y0ocotθo)−(k2Y0ecotθe+Y0ocotθo)

当耦合线微带线对称时即k=1k=1k=1时

Ysym=j2−(Y0ecot⁡θe+Y0ocot⁡θo)−(Y0ecot⁡θe−Y0ocot⁡θo)(Y0ecsc⁡θe+Y0ocsc⁡θo)(Y0ecsc⁡θe−Y0ocsc⁡θo)−(Y0ecot⁡θe−Y0ocot⁡θo)−(Y0ecot⁡θe+Y0ocot⁡θo)(Y0ecsc⁡θe−Y0ocsc⁡θo)(Y0ecsc⁡θe+Y0ocsc⁡θo)(Y0ecsc⁡θe+Y0ocsc⁡θo)(Y0ecsc⁡θe−Y0ocsc⁡θo)−(Y0ecot⁡θe+Y0ocot⁡θo)−(Y0ecot⁡θe−Y0ocot⁡θo)(Y0ecsc⁡θe−Y0ocsc⁡θo)(Y0ecsc⁡θe+Y0ocsc⁡θo)−(Y0ecot⁡θe−Y0ocot⁡θo)−(Y0ecot⁡θe+Y0ocot⁡θo) \mathbf{Y}{\text{sym}} = \frac{j}{2} \begin{bmatrix} -\left(Y{0e}\cot\theta_e + Y_{0o}\cot\theta_o\right) & -\left(Y_{0e}\cot\theta_e - Y_{0o}\cot\theta_o\right) & \left(Y_{0e}\csc\theta_e + Y_{0o}\csc\theta_o\right) & \left(Y_{0e}\csc\theta_e - Y_{0o}\csc\theta_o\right) \\8pt -\left(Y_{0e}\cot\theta_e - Y_{0o}\cot\theta_o\right) & -\left(Y_{0e}\cot\theta_e + Y_{0o}\cot\theta_o\right) & \left(Y_{0e}\csc\theta_e - Y_{0o}\csc\theta_o\right) & \left(Y_{0e}\csc\theta_e + Y_{0o}\csc\theta_o\right) \\8pt \left(Y_{0e}\csc\theta_e + Y_{0o}\csc\theta_o\right) & \left(Y_{0e}\csc\theta_e - Y_{0o}\csc\theta_o\right) & -\left(Y_{0e}\cot\theta_e + Y_{0o}\cot\theta_o\right) & -\left(Y_{0e}\cot\theta_e - Y_{0o}\cot\theta_o\right) \\8pt \left(Y_{0e}\csc\theta_e - Y_{0o}\csc\theta_o\right) & \left(Y_{0e}\csc\theta_e + Y_{0o}\csc\theta_o\right) & -\left(Y_{0e}\cot\theta_e - Y_{0o}\cot\theta_o\right) & -\left(Y_{0e}\cot\theta_e + Y_{0o}\cot\theta_o\right) \end{bmatrix} Ysym=2j −(Y0ecotθe+Y0ocotθo)−(Y0ecotθe−Y0ocotθo)(Y0ecscθe+Y0ocscθo)(Y0ecscθe−Y0ocscθo)−(Y0ecotθe−Y0ocotθo)−(Y0ecotθe+Y0ocotθo)(Y0ecscθe−Y0ocscθo)(Y0ecscθe+Y0ocscθo)(Y0ecscθe+Y0ocscθo)(Y0ecscθe−Y0ocscθo)−(Y0ecotθe+Y0ocotθo)−(Y0ecotθe−Y0ocotθo)(Y0ecscθe−Y0ocscθo)(Y0ecscθe+Y0ocscθo)−(Y0ecotθe−Y0ocotθo)−(Y0ecotθe+Y0ocotθo)